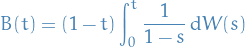Stochastic Differential Equations
Table of Contents
- Books
- Overview
- Notation
- Definitions
- Theorems
- Ito vs. Stratonovich
- Variations of Brownian motion
- Karhunen-Loève Expansion
- Diffusion Processes
- Solving SDEs
- Numerical SDEs
- Connections between PDEs and SDEs
- TODO Introduction to Stochastic Differential Equations
- Stochastic Partial Differential Equations (rigorous)
Books
- Handbook of Stochastic Methods
- Øksendal
- Probability with Martingales
Overview
- A lot from this section comes from the book lototsky2017stochastic
Notation
Correlation between two points of a random field or a random process:

to allow the possibility of an infinite number of points. In the discrete case this simply corresponds to the covariance matrix.
 denotes the Borel σ-algebra
denotes the Borel σ-algebra- Partition
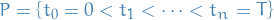
We write

Whenever we write stochastic integrals as Riemann sums, e.g.
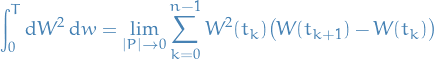
the limit is to be understood in the mean-square sense, i.e.
![\begin{equation*}
\mathbb{E} \Bigg[ \left| \int_{0}^{T} \dd{W}^2 \dd{w} - \bigg( \lim_{\left| P \right| \to 0} \sum_{k=0}^{n - 1} W^2(t_k) \big( W(t_{k + 1}) - W(t_k) \big) \bigg) \right|^2 \Bigg] \to 0
\end{equation*}](../../assets/latex/stochastic_differential_equations_2f41a4d7d8399bb2e7cfef31acb1c9ccdddb3dcf.png)
Definitions
A stochastic process  is called a either
is called a either
- second-order stationary
- wide-sense stationary
- weakly stationary
if
- the first moment
![$\mathbb{E}[X_t]$](../../assets/latex/stochastic_differential_equations_8d9f7fa24439190f383b035eaa73b879837215fa.png) is constant
is constant - covariance function depends only on the difference

That is,
![\begin{equation*}
\mathbb{E}[X_t] = \mu, \quad \mathbb{E} \Big[ \big( X_t - \mu \big) \big( X_s - \mu \big) \Big] = C(t - s)
\end{equation*}](../../assets/latex/stochastic_differential_equations_5ea8e1b4c47525a0c8a992b042b08df9e7214354.png)
A stochastic process is called (strictly) stationary if all FDDs are invariant under time translation, i.e. for all  , for all times
, for all times  , and
, and 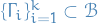 ,
,
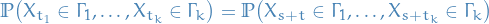
for  such that
such that  , for every
, for every  .
.
The autocorrelation function of a second-order stationary process enables us to associate a timescale to  , the correlation time
, the correlation time 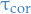 :
:
![\begin{equation*}
\tau_{\text{cor}} = \frac{1}{C(0)} \int_{0}^{\infty} C(\tau) \ d \tau = \frac{1}{\mathbb{E}[X_0^2]} \int_{0}^{\infty} \mathbb{E}[X_{\tau} X_0] \ d \tau
\end{equation*}](../../assets/latex/stochastic_differential_equations_587f96c122fe76cd3bcdf77e7c449c337aba8116.png)
Martingale continuous processes
Let
![$\{ \mathscr{F}_t \}_{t \in [0, T]}$](../../assets/latex/stochastic_differential_equations_a4f2239efacde13545eb8c98a02a871f2c9a18a6.png) be a filtration defined on the probability space
be a filtration defined on the probability space 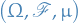
![$\{ X_t \}_{t \in [0, T]}$](../../assets/latex/stochastic_differential_equations_8e67cdfcf601ca9e21ebb401175755d9c3b1fc84.png) be to
be to  , i.e.
, i.e.  is measurable on
is measurable on  , with
, with  .
.
We say  is an
is an  martingale if
martingale if
![\begin{equation*}
\mathbb{E} \big[ X_t \mid \mathscr{F}_s \big] = X_s, \quad \forall t \ge s
\end{equation*}](../../assets/latex/stochastic_differential_equations_0ca720db7443e47a4e9a323ec4b3ae03dc11d8ff.png)
Gaussian process
A 1D continuous-time Gaussian process is a stochastic process for which  , and all finite-dimensional distributions are Gaussians.
, and all finite-dimensional distributions are Gaussians.
That is, for every finite dimensional vector

for some symmetric non-negative definite matrix  , for all
, for all  and
and  .
.
Theorems
Bochner's Theorem
Let  be a continuous positive definite function.
be a continuous positive definite function.
Then there exists a unique nonnegative measure  on
on  such that
such that 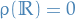 and
and

i.e.  is the Fourier transform of the function
is the Fourier transform of the function  .
.
Let  be a second-order stationary process with autocorrelation function
be a second-order stationary process with autocorrelation function  whose Fourier transform is
whose Fourier transform is 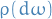 .
.
The measure 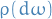 is called the spectral measure of the process
is called the spectral measure of the process  .
.
If the spectral measure is absolutely continuous wrt. the Lebesgue measure on  with density
with density  , i.e.
, i.e.

then the Fourier transform  of the covariance function is called the spectral density of the process:
of the covariance function is called the spectral density of the process:
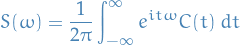
Ito vs. Stratonovich
- Purely matheamtical viewpoint: both Ito and Stratonovich calculi are correct
- Ito SDE is appropriate when continuous approximation of a discrete system is concerned
- Stratonovich SDE is appropriate when the idealization of a smooth real noise process is concerned
Benefits of Itô stochastic integral:
Benefits of Stratonovich stochastic integral:
- Leads to the standard Newton-Leibniz chain rule, in contrast to Itô integral which requires correction
- SDEs driven by noise with nonzero correlation time converge to the Stratonovich SDE, in the limit as the correlation time tends to 0
Practical considerations
- Rule of thumb:
- White noise is regarded as short-correlation approximation of a coloured noise → Stratonovich integral is natural
- "Expected" since the standard chain rule should work fro smooth noise with finite correlation
- White noise is regarded as short-correlation approximation of a coloured noise → Stratonovich integral is natural
Equivalence
Suppose  solves the following Stratonovich SDE
solves the following Stratonovich SDE

then  solves the Itô SDE:
solves the Itô SDE:

Suppose  solves the Itô SDE:
solves the Itô SDE:

then  solves the Stratonovich SDE:
solves the Stratonovich SDE:
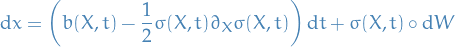
That is, letting  ,
,
- Stratonovich → Itô:
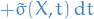
- Itô → Stratonovich:
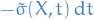
In the multidimensional case,
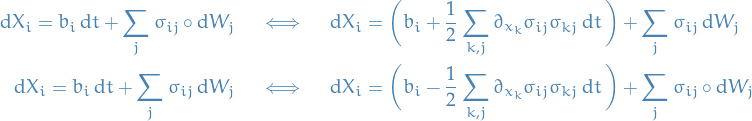
To show this we consider  staisfying the two SDEs
staisfying the two SDEs

i.e. the satisfying the stochastic integrals

We have
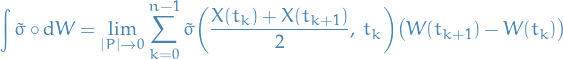
Equivalently, we can write
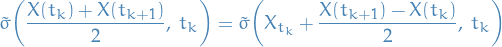
Assuming the  is smooth, we can then Taylor expand about
is smooth, we can then Taylor expand about  and evaluate at
and evaluate at 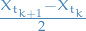 :
:
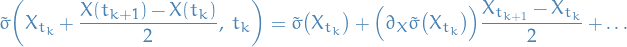
Substituting this back into the Riemann series expression for the Stratonovich integral, we have
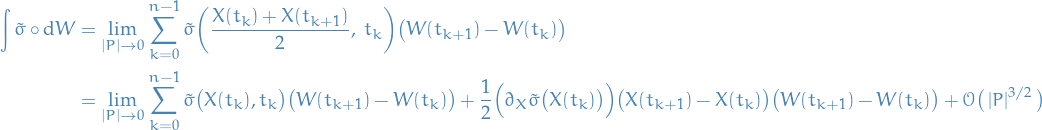
Using the fact that  satisfies the Itô integral, we have
satisfies the Itô integral, we have

and that
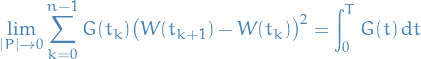
we get

Thus, we have the identity
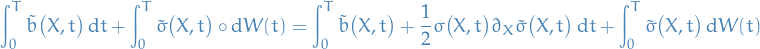
Matching the coefficients with the Itô integral satisfied by  , we get
, we get

which gives us the conversion rules between the Stratonovich and Itô formulation!
Important to note the following though: here we have assumed that the 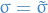 is smooth, i.e. infinitely differentiable and therefore locally Lipschitz. Therefore our proof only holds for this case.
is smooth, i.e. infinitely differentiable and therefore locally Lipschitz. Therefore our proof only holds for this case.
I don't know if one can relax the smoothness constraint of  and still obtain conversion rules between the two formulations of the SDEs.
and still obtain conversion rules between the two formulations of the SDEs.
Stratonovich satisfies chain rule proven using conversion
For some function 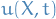 , one can show that the Stratonovich formulation satisfies the standard chain rule by considering the Stratonovich SDE, converting to Itô, apply Itô's formula, and then converting back to Stratonovich SDE!
, one can show that the Stratonovich formulation satisfies the standard chain rule by considering the Stratonovich SDE, converting to Itô, apply Itô's formula, and then converting back to Stratonovich SDE!
Variations of Brownian motion
Ornstein-Uhlenbeck process
Consider a mean-zero second-order stationary process with correlation function

We will write  , where
, where  .
.
The spectral density of this process is
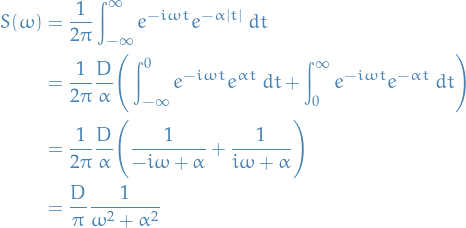
This  is called a Cauchy or Lorentz distribution.
is called a Cauchy or Lorentz distribution.
The correlation time is then
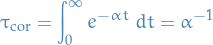
A real-valued Gaussian stationary process defiend on  with correlation function as given above is called a Ornstein-Uhlenbeck process.
with correlation function as given above is called a Ornstein-Uhlenbeck process.
Look here to see the derivation of the Ornstein-Uhlenbeck process from it's Markov semigroup generator.
Fractional Brownian Motion
A (normalized) fractional Brownian motion  ,
,  , with Hurst parameter
, with Hurst parameter  is a centered Gaussian process with continuous sample paths whose covariance is given by
is a centered Gaussian process with continuous sample paths whose covariance is given by
![\begin{equation*}
\mathbb{E} \Big[ W_t^H W_s^H \Big] = \frac{1}{2} \Big( s^{2 H } + t^{2 H} - |t - s|^{2H} \Big)
\end{equation*}](../../assets/latex/stochastic_differential_equations_1969cb5b42b869ff1006e5965ecc49ae84cbd5d4.png)
Hence, the Hurst parameter controls:
- the correlations between the increments of fractional Brownian motion
- the regularity of the paths: they become smoother as
 increases.
increases.
A fractional Brownian motion has the following properties
- When
 , then
, then 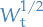 becomes standard Brownian motion.
becomes standard Brownian motion. We have
![\begin{equation*}
W_0^H = 0, \quad \mathbb{E} \Big[ \big(W_t^H\big)^2 \Big] = \left| t \right|^{2H}
\end{equation*}](../../assets/latex/stochastic_differential_equations_8c0d258d833885b8a8bd5c0580c7707f83dd0723.png)
It has stationary increments, and
![\begin{equation*}
\mathbb{E} \Big[ \big( W_t^H - W_s^H \big)^2 \Big] = \left| t- s \right|^{2H}
\end{equation*}](../../assets/latex/stochastic_differential_equations_e26c090c9022cb6663e364431a780f23248c560a.png)
It has the following self-similarity property:

where the equivalence is in law.
Karhunen-Loève Expansion
Notation
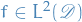 where
where 
 be an orthonormal basis in
be an orthonormal basis in 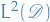
![$T = [0, 1]$](../../assets/latex/stochastic_differential_equations_23dced75d9a6ec5491322216c5886b4140c99f2e.png)
![$R(t, s) = \mathbb{E}[X_t X_s]$](../../assets/latex/stochastic_differential_equations_3b295160c01b3e49f52359d9016cb2bc6e61a130.png)
Stuff
Let ![$\mathscr{D} = [0, 1]$](../../assets/latex/stochastic_differential_equations_97cb4e38325c2c5a34d4a23d5f55de5c5e1b5204.png) .
.
Suppose
![\begin{equation*}
X_t(\omega) = \sum_{n=1}^{\infty} \xi_n(\omega) e_n(t), \quad t \in [0, 1]
\end{equation*}](../../assets/latex/stochastic_differential_equations_4a7cbe71aa0671bbd90019cc71a62e9ccd35b711.png)
We assume  are orthogonal or independent, and
are orthogonal or independent, and
![\begin{equation*}
\mathbb{E} \big[ \xi_n \xi_m \big] = \lambda_n \delta_{nm}
\end{equation*}](../../assets/latex/stochastic_differential_equations_e68b5cfb63a2da7f3d476bab49e1016d2c6ec9c5.png)
for some positive numbers  .
.
Then
![\begin{equation*}
\begin{split}
R(t, s) &= \mathbb{E}[X_t X_s] \\
&= \mathbb{E} \bigg( \sum_{k=1}^{\infty} \sum_{m=1}^{\infty} \xi_k e_k(t) \xi_m e_m(s) \bigg) \\
&= \sum_{k=1}^{\infty} \sum_{m=1}^{\infty} \mathbb{E}[\xi_k \xi_m] e_k(t) e_m(s) \\
&= \sum_{k=1}^{\infty} \lambda_k e_k(t) e_k(s)
\end{split}
\end{equation*}](../../assets/latex/stochastic_differential_equations_0f2c03172dac6146970a8f5b5085a3b654b1f040.png)
due to orthogonality of  and
and  for
for  .
.
Hence, for the expansion of  above, we need
above, we need  to be valid!
to be valid!
The above expression for  also implies
also implies
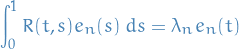
Hence, we also need the set  to be a set of eigenvalues and eigenvectors of the integral operator whose kernel is the correlation function of $Xt, i.e. need to study the operator
to be a set of eigenvalues and eigenvectors of the integral operator whose kernel is the correlation function of $Xt, i.e. need to study the operator
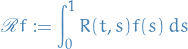
which we will now consider as an operator on ![$L^2 \big( [0, 1] \big)$](../../assets/latex/stochastic_differential_equations_e7126fcdebb9ebf5f71a45cf71db0142844a3b72.png) .
.
It's easy to see that  is self-adjoint and nonnegative in
is self-adjoint and nonnegative in  :
:

Furthermore, it is a compact operator, i.e. if  is a bounded sequence on
is a bounded sequence on  , then
, then  has a convergent subsequence.
has a convergent subsequence.
Spectral theorem for compact self-adjoint operators can be used to deduce that  has a countable sequence of eigenvalues tending to
has a countable sequence of eigenvalues tending to  .
.
Furthermore, for every 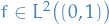 , we can write
, we can write
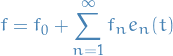
where  and
and  are the eigenfunctions of the operator
are the eigenfunctions of the operator  corresponding to the non-zero eigenvalues and where the convergence is in
corresponding to the non-zero eigenvalues and where the convergence is in  , i.e. we can "project"
, i.e. we can "project"  onto the subspace spanned by eigenfunctions of
onto the subspace spanned by eigenfunctions of  .
.
Let ![$\{ X_t, t \in [0, 1] \}$](../../assets/latex/stochastic_differential_equations_1225f44e89bcd169ffb7b1eb3ed517c6bd62dd9a.png) be an
be an  process with zero mean and continuous correlation function
process with zero mean and continuous correlation function  .
.
Let  be the eigenvalues and eigenfunctions of the operator
be the eigenvalues and eigenfunctions of the operator  defined
defined

Then
![\begin{equation*}
X_t = \sum_{n=1}^{\infty} \xi_n e_n(t), \quad t \in [0, 1]
\end{equation*}](../../assets/latex/stochastic_differential_equations_070cf4e790d3c037f3d71d457cd9e629ce3043c9.png)
where
![\begin{equation*}
\begin{split}
\xi_n &= \int_{0}^{1} X_t e_n(t) \ dt \\
\mathbb{E} \big[ \xi_n \big] &= 0 \\
\mathbb{E} \big[ \xi_n \xi_m \big] &= \lambda \delta_{n m}
\end{split}
\end{equation*}](../../assets/latex/stochastic_differential_equations_7b5cbc1b279426a8986865434401a8231ef5e979.png)
The series converges in  to
to  , uniformly in
, uniformly in  !
!
Karhunen-Loève expansion of Brownian motion
- Correlation function of Brownian motion is
 .
. Eigenvalue problem
 becomes
becomes

- Assume
 (since
(since  would imply ψn(t) = 0$)
would imply ψn(t) = 0$) - Consider intial condition
 which gives
which gives 
Can rewrite eigenvalue problem

Differentiatiate once
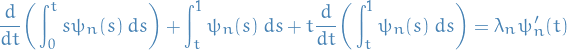
using FTC, we have
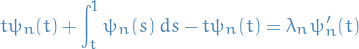
hence
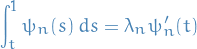
- Obtain second BC by observing
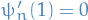 (since LHS in the above is clearly 0)
(since LHS in the above is clearly 0) Second differentiation

Thus, the eigenvalues and eigenfunctions of the integral operator whose kernel is the covariance function of Brownian motion can be obtained as solutions to the Sturm-Lioville problem

Eigenvalues and (normalized) eigenfunctions are then given by
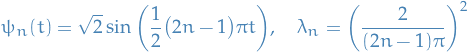
Karhunen-Loève expansion of Brownian motion on
![$[0, 1]$](../../assets/latex/stochastic_differential_equations_68c8fa38d960e53d4308cbf1e65d04c66a554817.png) is then
is then
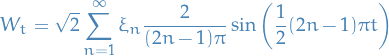
Diffusion Processes
Notation
Markov Processes and the Chapman-Kolmogorov Equation
We define the σ-algebra generated by  , denoted
, denoted  , to be the smallest σ-algebra s.t. the family of mappings
, to be the smallest σ-algebra s.t. the family of mappings  is a stochastic process with
is a stochastic process with
- sample space
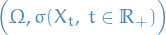
- state space
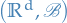
- Idea: encode all past information about a stochastic process into an appropriate collection of σ-algebras
Let 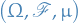 denote a probability space.
denote a probability space.
Consider stochastic process 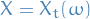 with
with  and state space
and state space 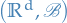 .
.
A filtration on 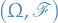 is a nondecreasing family
is a nondecreasing family  of sub-σ-algebras of
of sub-σ-algebras of  :
:

We set
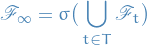
Note that  is a possibility.
is a possibility.
The filtration generated by or natural filtration of the stochastic process  is
is

A filtration  is generated by events of the form
is generated by events of the form

with  and
and  .
.
Let  be a stochastic process defined on a probability space
be a stochastic process defined on a probability space 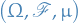 with values in
with values in 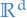 , and let
, and let  be the filtration generated by
be the filtration generated by  .
.
Then  is a Markov process if
is a Markov process if

for all  with
with  , and
, and  .
.
Equivalently, it's a Markov process if
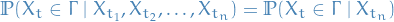
for  and
and  with
with  .
.
Chapman-Kolmogorov Equation
The transition function  for fixed
for fixed  is a probability measure on
is a probability measure on 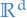 with
with

It is  measurable in
measurable in  , for fixed
, for fixed 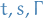 , and satisfies the Chapman-Kolmogorov equation
, and satisfies the Chapman-Kolmogorov equation

for all


 with
with 
Assuming that 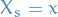 , we can write
, we can write
![\begin{equation*}
P(\Gamma, t \mid x, s ) = \mathbb{P} \big[ X_t \in \Gamma \mid X_s = x \big]
\end{equation*}](../../assets/latex/stochastic_differential_equations_a2caf2b6f9a9de649a064e6bcf54c04f6f39838d.png)
since ![$\mathbb{P} \big[ X_t \in \Gamma \mid \mathscr{F}_s^X \big] = \mathbb{P} \big[ X_t \in \Gamma \mid X_s \big]$](../../assets/latex/stochastic_differential_equations_eac94ebb86be9c955d319e80319525a5e83f2e6c.png) .
.
In words, the Chapman-Kolmogorov equation tells us that for a Markov process, the transition from  at time
at time  to the set
to the set  at time
at time  can be done in two steps:
can be done in two steps:
- System moves from
 to
to  at some intermediate step
at some intermediate step 
- Moves from
 to
to  at time
at time 
Generator of a Markov Process
Chapman-Kolmogorov equation suggests that a time-homogenous Markov process can be described through a semigroup of operators, i.e. a one-parameter family of linear operators with the properties
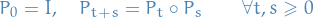
Let  be the transition function of a homogenous Markov process and let
be the transition function of a homogenous Markov process and let  , and define the operator
, and define the operator
![\begin{equation*}
\big( P_t f \big)(x) := \mathbb{E} \Big[ f(X_t) \mid X_0 = x \Big] = \int_{\mathbb{R}^d}^{} f(y) \ P(t, x, dy)
\end{equation*}](../../assets/latex/stochastic_differential_equations_650c4cf9438bd1c8253e889eaba8a58ce2cf59af.png)
Linear operator with
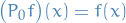
which means that 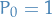 , and
, and

i.e.  .
.
We can study properties of time-homogenous Markov process  by studying properties of the Markov semigroup
by studying properties of the Markov semigroup  .
.
This is an example of a strongly continuous semigroup.
Let 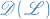 be set of all
be set of all  such that the limit
such that the limit
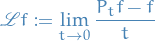
exists.
The operator  is called the (infinitesimal) generator of the operator semigroup
is called the (infinitesimal) generator of the operator semigroup 
- Also referred to as the generator of the Markov process

This is an example of a (infinitesimal) generator of a strongly continuous semigroup.
The semigroup property of the generator of the Markov process implies that we can write
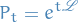
Furthermore, consider function
![\begin{equation*}
u(x, t) = \big( P_t f \big)(x) = \mathbb{E} \Big[ f(X_t) \mid X_0 = x \Big]
\end{equation*}](../../assets/latex/stochastic_differential_equations_f32e574b9643a44a3640f02130ba9d0f43bf51ac.png)
Compute time-derivative
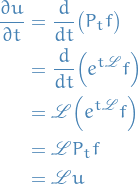
And we also have

Consequently,  satisfies the IVP
satisfies the IVP
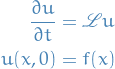
which defines the backward Kolmogorov equation.
This equation governs the evolution of the expectation of an observalbe  .
.
Example: Brownian motion 1D
- Transition function for Brownian motion is given by the fundamental solution to the heat equation in 1D
Corresponding Markov semigroup is the heat semigroup
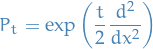
- Generator of the 1D Brownian motion is then the 1D Laplacian
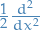
The backward Kolmorogov equation is then the heat equation
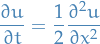
Adjoint semigroup
Let  be a Markov semigroup, which then acts on
be a Markov semigroup, which then acts on  .
.
The adjoint semigroup  acts on probability measures:
acts on probability measures:
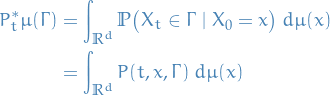
The image of a probability measure  under
under  is again a probability measure.
is again a probability measure.
The operators  and
and  are adjoint in the
are adjoint in the  sense:
sense:
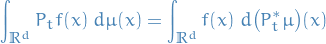
We can write
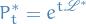
where  is the
is the  adjoint of the generator of the Markov process:
adjoint of the generator of the Markov process:
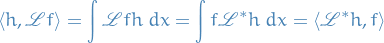
Let  be a Markov process with generator
be a Markov process with generator  with
with  , and let
, and let  denote the adjoint Markov semigroup.
denote the adjoint Markov semigroup.
We define
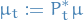
This is the law of the Markov process. This follows the equation
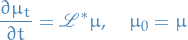
Assuming that the initial distribution  and the law of the process
and the law of the process  each have a density wrt. Lebesgue measure, denoted
each have a density wrt. Lebesgue measure, denoted  and
and  , respectively, the law becomes
, respectively, the law becomes

which defines the forward Kolmorogov equation.
"Simple" forward Kolmogorov equation
Consider SDE

Since
 is Markovian, its evoluation can be characterised by a transition probability
is Markovian, its evoluation can be characterised by a transition probability  :
:
![\begin{equation*}
\mathbb{P} \Big( X(t) \in [x, x + \dd{t}] : X(s) = y \Big) = p(x, t \mid y, s) \dd{x}
\end{equation*}](../../assets/latex/stochastic_differential_equations_df4f6b62ca1e95add6d6557ce08703c3e1d270b6.png)
Consider
 , then
, then
![\begin{equation*}
\dd{\Big( f \big( X(u) \big) \Big)} = \partial_x f \Big( X(u) \Big) \Big[ b \big( X(u), u \big) \dd{u} + \sigma \big( X(u), u \big) \dd{W} \Big] + \frac{1}{2} \partial_{xx} f \Big( X(u) \Big) \sigma^2 \Big( X(u), u \Big) \dd{u}
\end{equation*}](../../assets/latex/stochastic_differential_equations_b96cbc3de78139e9888f72b2385039877196203a.png)
Ergodic Markov Processes
Using the adjoint Markov semigroup, we can define the invariant measure as a probability measure that is invariant under time evolution of  , i.e. a fixed point of the semigroup
, i.e. a fixed point of the semigroup  :
:

A Markov process is said to be ergodic if and only if there exists a unique invariant measure  .
.
We say the process is ergodic wrt. the measure  .
.
Furthermore, if we consider a Markov process  in
in 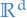 with generator
with generator  and Markov semigroup
and Markov semigroup  , we say that
, we say that  is ergodic provided that
is ergodic provided that  is a simple eigenvalue of
is a simple eigenvalue of  , i.e.
, i.e.

has only constant solutions.
Thus, we can study the ergodic properties of a Markov process  by studying the null space of the its generator.
by studying the null space of the its generator.
We can then obtain an equation for the invariant measure in terms of the adjoint  of the generator.
of the generator.
Assume that  has a density
has a density  wrt. the Lebesgue measure. Then
wrt. the Lebesgue measure. Then
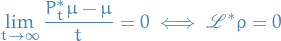
by definition of the generator of the adjoint semigroup.
Furthermore, the long-time average of an observable  converges to the equilibrium expectation wrt. the invariant measure
converges to the equilibrium expectation wrt. the invariant measure

1D Ornstein-Uhlenbeck process and its generator
The 1D Ornstein-Uhlenbeck process is an ergodic Markov process with generator
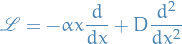
The null-space of  comprises of constants in
comprises of constants in  , hence it is an ergodic Markov process.
, hence it is an ergodic Markov process.
In order to find the invariant measure, we need to solve the stationary Fokker-Planck equation:

Which clearly require that we have an expression for  . We have
. We have  , so
, so
![\begin{equation*}
\begin{split}
\int_{\mathbb{R}}^{} \mathscr{L}f \ h \ dx &= \int_{\mathbb{R}}^{} \bigg[ \bigg( - \alpha x \frac{df}{dx} \bigg) + \bigg( D \frac{d^2 f}{dx^2} \bigg) \bigg] \ dx \\
&= \int_{\mathbb{R}}^{} \Big[ f \partia_x \big( \alpha x h \big) + f \big( D \partial_x^2 h \big) \Big] \ dx \\
&=: \int_{\mathbb{R}}^{} f \mathscr{L}^* h \ dx
\end{split}
\end{equation*}](../../assets/latex/stochastic_differential_equations_e09dc286790d97633168df255296229a360c69b5.png)
Thus,
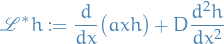
Substituting this expression for  back into the equation above, we get
back into the equation above, we get

which is just a Gaussian measure!
Observe that in the above expression, the stuff on LHS before  corresponds to
corresponds to  in the equation we solved for
in the equation we solved for  .
.
If  (i.e. distributed according to the invariant measure
(i.e. distributed according to the invariant measure  derived above), then
derived above), then  is a mean-zero Gaussian second-order stationary process on
is a mean-zero Gaussian second-order stationary process on  with correlation function
with correlation function
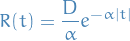
and spectral density
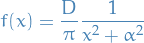
as seen before!
Furthermore, Ornstein-Uhlenbeck process is the only real-valued mean-zero Gaussian second-order stationary Markov process with continuous paths defined on  .
.
Diffusion Processes
Notation
 means depends on terms dominated by linearity in
means depends on terms dominated by linearity in 
Stuff
A Markov process consists of three parts:
- a drift
- a random part
- a jump process
A diffusion process is a Markov process with no jumps.
A Markov process  in
in  with transition function
with transition function  is called a diffusion process if the following conditions are satisfied:
is called a diffusion process if the following conditions are satisfied:
(Continuity) For every
 and
and  ,
,

uniformly over

( Drift coefficient ) There exists a function
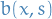 s.t. for every
s.t. for every  and every
and every  ,
,
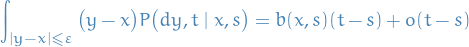
uniformly over
 .
.
( Diffusion coefficient ) There exists a function
 s.t. for every
s.t. for every  and every
and every  ,
,
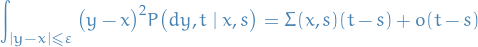
uniformly over
 .
.
Important: above we've truncated the domain of integration, since we do not know whether the first and second moments of  are finite. If we assume that there exists
are finite. If we assume that there exists  such that
such that
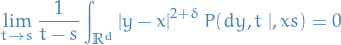
then we can extend integration over all of  and use expectations in the definition of the drift and the diffusion coefficient , i.e. the drift:
and use expectations in the definition of the drift and the diffusion coefficient , i.e. the drift:
![\begin{equation*}
\lim_{t \to s} \mathbb{E} \bigg[ \frac{X_t - X_s}{t - s} \bigg| X_s = x \bigg] = b(x, s)
\end{equation*}](../../assets/latex/stochastic_differential_equations_1a3b70c34987a635cd59988bc20315b883cf348e.png)
and diffusion coefficient:
![\begin{equation*}
\lim_{t \to s} \mathbb{E} \bigg[ \frac{\left| X_t - X_s \right|^2}{t - s} \bigg| X_s = x \bigg] = \Sigma(x, s)
\end{equation*}](../../assets/latex/stochastic_differential_equations_7b7e831fbb6901407e7a79fa490c7e5b5ada2474.png)
Backward Kolmogorov Equation
Let  , and let
, and let
![\begin{equation*}
u(x, s) := \mathbb{E} \Big[ f(X_t) \mid X_s = x \Big] = \int_{}^{} f(y) \ P(dy, t \mid x, s)
\end{equation*}](../../assets/latex/stochastic_differential_equations_3fcabfeb4cba60a7f3d3bc9bcd9c38a8e8afb88c.png)
with fixed  .
.
Assume, furthermore, that the functions 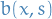 and
and  are smooth in both
are smooth in both  and
and  .
.
Then  solves the final value problem
solves the final value problem

for ![$s \in [0, t]$](../../assets/latex/stochastic_differential_equations_a01cab2a0ca7fa7a95b9372d9031b49f2bd03f76.png) .
.
For a proof, see Thm 2.1 in pavliotis2014stochastic. It's clever usage of the Chapman-Kolmogorov equation and Taylor's theorem.
For a time-homogenous diffusion process, where the drift and the diffusion coefficents are independent of time:

we can rewrite the final value problem defined by the backward Kolmogorov equation as an initial value problem.
Let  , and introduce
, and introduce  . Then,
. Then,
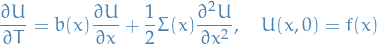
Further, we can let  , therefore
, therefore
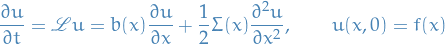
where
![\begin{equation*}
u(x, t) = \mathbb{E} \Big[ f(X_t) \mid X_0 = x \Big]
\end{equation*}](../../assets/latex/stochastic_differential_equations_453e5e2378adb55ddec75660c12a82c4813b1c20.png)
is the solution to the IVP.
Forward Kolmorogov Equation
Assume that the conditions of a diffusion process are satisfied, and that the following are smooth functions of 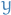 and
and  :
:
Then the transition probability density is the solution to the IVP

For proof, see Thm 2.2 in pavliotis2014stochastic. It's clever usage of Chapman-Kolmogorov equation.
Solving SDEs
This section is meant to give an overview over the calculus of SDEs and tips & tricks for solving them, both analytically and numerically. Therefore this section might be echoing other sections quite a bit, but in a more compact manner most useful for performing actual computations.
Notation
Analytically
"Differential calculus"
 =
= 
 for all
for all 
If multivariate case, typically one will assume white noise to be indep.:

Suppose we have some SDE for
 , i.e. some expression for
, i.e. some expression for  .
Change of variables
.
Change of variables  then from Itô's lemma we have
then from Itô's lemma we have
where
 is computed by straight forward substitution by expression for
is computed by straight forward substitution by expression for 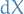 and using the "properties" of
and using the "properties" of 
Letting
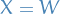 and
and  in Itô's lemma we get
in Itô's lemma we get

Letting
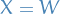 and
and  , then Itô's lemma gets us
, then Itô's lemma gets us
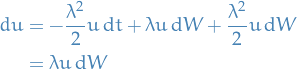
Hence
 satisfies the geometric Brownian motion SDE.
satisfies the geometric Brownian motion SDE.
Numerically
Numerical SDEs
Notation

We willl consider an SDE with the exact solution

Convergence
The strong error is defined
![\begin{equation*}
e_{\Delta t}^{\text{strong}} := \sup_{0 \le t_n \le T} \mathbb{E} \big[ \left| X_n - X(t_n) \right| \big]
\end{equation*}](../../assets/latex/stochastic_differential_equations_68efec6daabf5c6f11a5e4ad62da5dce62abc462.png)
We say a method converges strongly if
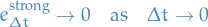
We say the method has strong order  if
if

Basically, this notion of convergence talks about how "accurately" paths are followed.
Error on individual path level
Euler-Maryuama has
![\begin{equation*}
\mathbb{E} \big[ \left| X_n - X(t_n) \right| \big] \le K \Delta t ^{\frac{1}{2}}
\end{equation*}](../../assets/latex/stochastic_differential_equations_44c28c2bdca36e182b6cb2ac704fc867961d9520.png)
Markov inequality says
![\begin{equation*}
\mathbb{P} \big( \left| X \right| > \alpha \big) \le \frac{\mathbb{E} \big[ \left| X \right| \big]}{\alpha}
\end{equation*}](../../assets/latex/stochastic_differential_equations_1d59e14e6a22a2a668a50fd9912b2fbb8d39ea49.png)
for any
 .
.
Let
 gives
gives

i.e.

- That is, along any path the error is small with high probability
Stochastic Taylor Expansion
Deterministic ODEs
Consider
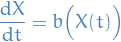
For some function, we then write
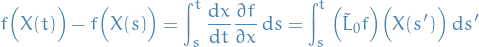
where

and the
 is due to the above
is due to the above
- This looks quite a bit like the numerical quadrature rule, dunnit kid?!
- Because it is!
We can then do the same for
 :
:
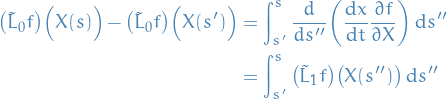
where
![\begin{equation*}
\big( \tilde{L}_1 f \big) \big( X(t) \big) = \dv{}{t} \bigg( \dv{x}{t} \frac{\partial f}{\partial x} \bigg) = \dv[2]{x}{t} \frac{\partial f}{\partial x} + \bigg( \dv{x}{t} \bigg)^2 \pdv[2]{f}{x}
\end{equation*}](../../assets/latex/stochastic_differential_equations_5f1ba462ce108266e939340b4242c04356adf851.png)
- We can then substitute this back into the original integral, and so on, to obtain higher and higher order
- This is basically just performing a Taylor expansion around a point wrt. the stepsize

- For an example of this being used in a "standard" way; see how we proved Euler's method for ODEs
- Reason for using integrals rather than the the "standard" Taylor expansion to motivate the stochastic way of doing this, where we cannot properly talk about taking derivatives
Stochastic
- Idea: extend the "Taylor expansion method" of obtaining higher order numerical methods for ODEs to SDEs
Consider

Satisfies the Itô integral
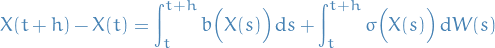
- Can do the same as before for each of the integral terms:
 :
:
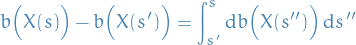
but in this stochastic case, we have to use Itô's formula
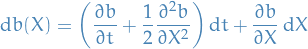
so
![\begin{equation*}
b \Big( X(s) \Big) - b \Big( X(s') \Big) = \frac{1}{2} \int_{s'}^{s} \pdv[2]{b}{X} \dd{s''} + \int_{s'}^{s} \pdv{b}{X} \dd{X(s'')}
\end{equation*}](../../assets/latex/stochastic_differential_equations_9952697df75c5a4e9be4c5932214801fa5c663d1.png)
 :
:
![\begin{equation*}
\sigma \Big( X(s) \Big) - \sigma \Big( X(s') \Big) = \frac{1}{2} \int_{s'}^{s} \pdv[2]{\sigma}{X} \dd{s''} + \int_{s'}^{s} \pdv{\sigma}{X} \dd{X(s'')}
\end{equation*}](../../assets/latex/stochastic_differential_equations_2853365c0d2abf6ff232b39e764a79d466e1ee33.png)
Then we can substitute these expressions into our original expression for
 :
:
![\begin{equation*}
\begin{split}
X(t + h) - X(t) &= \int_{t}^{t + h} \bigg[ b \big( X(s') \big) + \frac{1}{2} \int_{s'}^{s} \pdv[2]{b}{X} \dd{s''} + \int_{s'}^{s} \pdv{b}{X} \dd{X(s'')} \bigg] \dd{s} \\
& \quad + \int_{t}^{t + h} \bigg[ \sigma \Big( X(s') \Big) + \frac{1}{2} \int_{s'}^{s} \pdv[2]{\sigma}{X} \dd{s''} + \int_{s'}^{s} \pdv{\sigma}{X} \dd{X(s'')} \bigg] \dd{W(s)}
\end{split}
\end{equation*}](../../assets/latex/stochastic_differential_equations_50aa343322e20485f21a70fb9ad0a279ad24f093.png)
Observe that we can bring the terms
 and
and  out of the integrals:
out of the integrals:
![\begin{equation*}
\begin{split}
X(t + h) - X(t) &= b \big( X(s') \big) \underbrace{\int_{t}^{t + h} \dd{s}}_{= h} + \int_{t}^{t + h} \bigg[ \frac{1}{2} \int_{s'}^{s} \pdv[2]{b}{x} \dd{s''} + \int_{s'}^{s} \pdv{b}{X} \dd{X(s'')} \bigg] \dd{s} \\
& \quad + \sigma \big( X(s') \big) \underbrace{\int_{t}^{t + h} \dd{W(s)}}_{= W(t + h) - W(t) = \Delta W} \\
& \quad + \int_{t}^{t + h} \bigg[ \frac{1}{2} \int_{s'}^{s} \pdv[2]{\sigma}{X} \dd{s''} + \int_{s'}^{s} \pdv{\sigma}{X} \dd{X(s'')} \bigg] \dd{W(s)} \\
&= b \big( X(s') \big) h + \int_{t}^{t + h} \bigg[ \frac{1}{2} \int_{s'}^{s} \pdv[2]{b}{x} \dd{s''} + \int_{s'}^{s} \pdv{b}{X} \dd{X(s'')} \bigg] \dd{s} \\
& \quad + \sigma \big( X(s') \big) \Delta W + \int_{t}^{t + h} \bigg[ \frac{1}{2} \int_{s'}^{s} \pdv[2]{\sigma}{X} \dd{s''} + \int_{s'}^{s} \pdv{\sigma}{X} \dd{X(s'')} \bigg] \dd{W(s)}
\end{split}
\end{equation*}](../../assets/latex/stochastic_differential_equations_e47f65fbc312ada51b9c299b272a10858dce4176.png)
- Observe that the two terms that we just brought out of the integrals define the Euler-Maruyama method!!
- Bloody dope, ain't it?
Connections between PDEs and SDEs
Suppose we have an SDE of the form

Forward Kolmogorov / Fokker-Plank equation
Then the Fokker-Planck / Forward Kolmogorov equation is given by the following ODE:
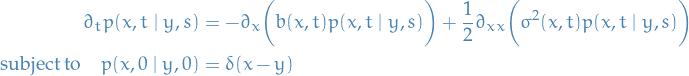
Derivation of Forward Kolmogorov
Suppose we have an SDE of the form

Consider twice differentiable function  , then Itô's formula gives us
, then Itô's formula gives us
![\begin{equation*}
\begin{split}
\dd{f \big( X(t) \big)} &= \partial_t f \big( X(t) \big) \dd{t} + \partial_x f \big( X(t) \big) \dd{X(t)} + \frac{1}{2} \partial_{xx} f \big( X(t) \big) \big( \dd{X(t)} \big)^2 \\
&= \partial_x f \big( X(t) \big) \Big[ b \big( X(t), t \big) \dd{t} + \sigma^2 \big( X(t), t \big) \dd{W(t)} \Big] + \frac{1}{2} \partial_{xx} f \big( X(t) \big) \dd{t}
\end{split}
\end{equation*}](../../assets/latex/stochastic_differential_equations_5c66131e332963d70a943a25bd03efe68d3142d9.png)
which then satisfies the Itô integral
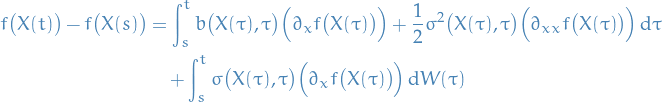
Taking the (conditional) expectation, the last term vanish, so LHS becomes
![\begin{equation*}
\begin{split}
\mathbb{E} \Big[ f \big( X(t) \big) - f \big( X(s) \big) \mid X(s) = x_0 \Big] &= \mathbb{E} \Big[ f \big( X(t) \big) \mid X(s) = x_0 \Big] - f(x_0) \\
&= \bigg( \int_{}^{} f( x ) p(x, t \mid x_0, s) \dd{x} \bigg) - f(x_0)
\end{split}
\end{equation*}](../../assets/latex/stochastic_differential_equations_7af9f83c50a8d955ceaef50bacea3cc649c1d9fd.png)
and RHS
![\begin{equation*}
\begin{split}
& \mathbb{E} \Bigg[ \int_{s}^{t} b \big( X(\tau), \tau \big) \Big( \partial_x f \big( X(\tau) \big) \Big) + \frac{1}{2} \sigma^2 \big( X(\tau), \tau \big) \Big( \partial_{xx} f \big( X(\tau) \big) \Big) \dd{\tau} \ \bigg| \ X(s) = x_0 \Bigg] \\
= \quad & \int_{}^{} \bigg( \int_{s}^{t} p(x, \tau \mid x_0, s) \bigg[ b \big( x, \tau \big) \Big( \partial_x f(x) \Big) + \frac{1}{2} \sigma^2 \big( x, \tau \big) \Big( \partial_{xx} f (x) \Big) \bigg] \dd{\tau} \bigg) \dd{x}
\end{split}
\end{equation*}](../../assets/latex/stochastic_differential_equations_221076c0f59c76cc297abf9cdd940b1dc1c3c055.png)
Taking the derivative wrt.  , LHS becomes
, LHS becomes

and RHS
![\begin{equation*}
\int p(x, t \mid x_0, s) \bigg[ b \big( x, t \big) \Big( \partial_x f(x) \Big) + \frac{1}{2} \sigma^2 \big( x, t \big) \Big( \partial_{xx} f (x) \Big) \bigg] \dd{x}
\end{equation*}](../../assets/latex/stochastic_differential_equations_79869131775111ee7c958dd3802537ac57499d76.png)
The following is actually quite similar to what we do in variational calculus for our variations!
Here we first use the standard "integration by parts to get  rather than derivatives of
rather than derivatives of  ", and then we make use of the Fundamental Lemma of the Calculus of Variations!
", and then we make use of the Fundamental Lemma of the Calculus of Variations!
Using integration by parts in the above equation for RHS, we have
![\begin{equation*}
\int \bigg[ - \partial_x \Big( p(x, t \mid x_0, s) b(x, t) \Big) + \frac{1}{2} \partial_{xx} \Big( p(x, t \mid x_0, s) \sigma^2(x, t) \Big) \bigg] f(x) \dd{x}
\end{equation*}](../../assets/latex/stochastic_differential_equations_33c80d5bb4ce09dc3587f5afdab2ea378df16f48.png)
where we have assumed that we do not pick up any extra terms (i.e. the functions vanish at the boundaries). Hence,
![\begin{equation*}
\int f(x) \Big( \partial_t p(x, t \mid x_0, s) \Big) \dd{x} = \int \bigg[ - \partial_x \Big( p(x, t \mid x_0, s) b(x, t) \Big) + \frac{1}{2} \partial_{xx} \Big( p(x, t \mid x_0, s) \sigma^2(x, t) \Big) \bigg] f(x) \dd{x}
\end{equation*}](../../assets/latex/stochastic_differential_equations_b9c93801fa9da8ed2e26ae06d732730b2a68c597.png)
Since this holds for all  , by the Fundamental Lemma of Calculus of Variations, we need
, by the Fundamental Lemma of Calculus of Variations, we need

which is the Fokker-Planck equation, as wanted!
Assumptions
In the derivation above we assumed that the non-integral terms vanished when we performed integration by parts. This is really assuming one of the following:
- Boundary conditions at
 :
:  as
as 
- Absorbing boundary conditions: where we assume that
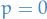 for
for  (the boundary of the domain
(the boundary of the domain  )
) - Reflecting boundary conditions: this really refers to the fact that multidimensional variations vanish has vanishing divergence at the boundary. See multidimensional Euler-Lagrange and the surrounding subjects.
Backward equation
And the Backward Kolmogorov equation:
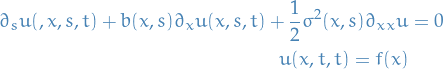
where
![\begin{equation*}
u(x, s, t) = \big( P_t f \big)(x) = \mathbb{E} \Big[ f \big( X(t) \big) \mid X(s) = x \Big], \quad t \ge s
\end{equation*}](../../assets/latex/stochastic_differential_equations_c5f7341f119d84d5d47e34f5b4bc0505f5b7085b.png)
Here we've used  defined as
defined as
![\begin{equation*}
\big( P_t f \big)(x) = \mathbb{E} \Big[ f \big( X(t) \big) \mid X(s) = x \Big]
\end{equation*}](../../assets/latex/stochastic_differential_equations_cb500821636d36ac05c4726b19225eced9685e83.png)
rather than
![\begin{equation*}
\big( P_t f \big)(x) = \mathbb{E} \Big[ f \big( X(t) \big) \mid X(0) = x \Big]
\end{equation*}](../../assets/latex/stochastic_differential_equations_b1926b7478d755d25ab8c049fc27c78953ad4314.png)
as defined before.
I do this to stay somewhat consistent with notes in the course (though there the operator  is not mentioned explicitly), but I think using
is not mentioned explicitly), but I think using  would simplify things without loss of generality (could just define the equations using
would simplify things without loss of generality (could just define the equations using  and
and 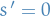 , and substitute back when finished).
, and substitute back when finished).
Furthermore, if  and
and  , i.e. time-independent (autonomous system), then
, i.e. time-independent (autonomous system), then

in which case the Forward Kolmogorov equation becomes
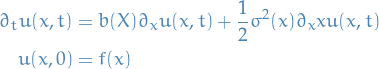
where we've used the fact that in this case 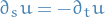 .
.
Notation of generator of the Markov process and its adjoint
In the notation of the generator of the Markov process we have
![\begin{equation*}
\begin{split}
\mathcal{L} u &= b(x, t) \pdv{u}{x} + \frac{1}{2} \sigma^2(x, t) \pdv[2]{u}{t} \\
\mathcal{L}^* \rho &= - \pdv{}{x} \Big( b(x, t) \rho \Big) + \frac{1}{2} \pdv[2]{}{x} \Big( \sigma^2(x, t) \rho \Big)
\end{split}
\end{equation*}](../../assets/latex/stochastic_differential_equations_aad09fdd9f274ca752316028b16d9df7ece8cc8e.png)
TODO Introduction to Stochastic Differential Equations
Notation
 indicates the dependence on the initial condition
indicates the dependence on the initial condition  .
.Stopping time
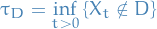
Motivation
We will consider stochastic differential equations of the form

or, equivalently, componentwise,

which is really just notation for

Need to define stochastic integral

for sufficiently large class of functions.
- Since Brownian motion is not of bounded variation → Riemann-Stieltjes integral cannot be defined in a unique way
Itô and Stratonovich Stochastic Integrals
Let
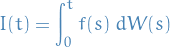
where  is a Brownian motion and
is a Brownian motion and ![$t \in [0, T]$](../../assets/latex/stochastic_differential_equations_a2d5fb401a604a95248d145edaa967973c136562.png) , such that
, such that
![\begin{equation*}
\mathbb{E} \bigg[ \int_{0}^{T} f(s)^2 \ ds \bigg] < \infty
\end{equation*}](../../assets/latex/stochastic_differential_equations_6923cd2757f7af08ca383a9c451640fd55daedc7.png)
Integrand is a stochastic process whose randomness depends on  , and in particular, that is adapted to the filtration
, and in particular, that is adapted to the filtration  generated by the Brownian motion
generated by the Brownian motion  , i.e. that is an
, i.e. that is an  function for all
function for all ![$t \in [0, T]$](../../assets/latex/stochastic_differential_equations_a2d5fb401a604a95248d145edaa967973c136562.png) .
.
Basically means that the integrand depends only on the past history of the Brownian motion wrt. which we are integrating.
We then define the stochastic integral  as the
as the  (
( is the underlying probability space) limit of the Riemann sum approximation
is the underlying probability space) limit of the Riemann sum approximation
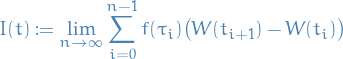
where
 where
where  is s.t.
is s.t. 
![$\lambda \in [0, 1]$](../../assets/latex/stochastic_differential_equations_7cd670af2080b3c73aac2cd9f356000145119694.png)
increments

What we are really saying here is that  (which itself is a random variable, i.e. a measurable function on the probability space
(which itself is a random variable, i.e. a measurable function on the probability space  ) is the limit of the Riemann sum in a mean-square sense, i.e. converges in
) is the limit of the Riemann sum in a mean-square sense, i.e. converges in  !
!
![\begin{equation*}
\begin{split}
& \mathbb{E} \Bigg[ \left| I(t) - \lim_{n \to \infty} \sum_{i=0}^{n - 1} f(\tau_i) \big( W(t_{i + 1}) - W(t_i) \big) \right|^2 \Bigg] \\
& \quad = \int_{\Omega} \left| I(t) - \lim_{n \to \infty} \sum_{i=0}^{n - 1} f(\tau_i) \big( W(t_{i + 1}) - W(t_i) \big) \right|^2 \dd{P} \\
& \quad = 0
\end{split}
\end{equation*}](../../assets/latex/stochastic_differential_equations_5ab3f253cbbe4e45691de5ac5b088d29ad66f5bb.png)
I found this Stackexchange answer to be very informative regarding the use of Riemann sums to define the stochastic integral.
Let  be a stochastic integral.
be a stochastic integral.
The Stratonovich stochastic integral is when  , i.e.
, i.e.
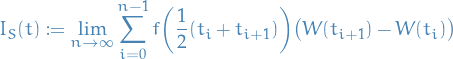
We will often use the notation
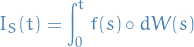
to denote the Stratonovich stochastic integral.
Observe that  does not satisfy the Martingale property, since we are taking the midpoint in
does not satisfy the Martingale property, since we are taking the midpoint in ![$[t_k, t_{k + 1}]$](../../assets/latex/stochastic_differential_equations_cb683a2b95e8f305f3febcbd22819f76e61ab375.png) , therefore
, therefore 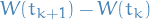 is correlated with
is correlated with  !
!
Itô instead uses the Martingale property by evaluating  at the start point of the integral, and thus there is no auto correlation between the
at the start point of the integral, and thus there is no auto correlation between the  and
and  , making it much easier to work with.
, making it much easier to work with.
Suppose that there exist 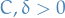 s.t.
s.t.
![\begin{equation*}
\mathbb{E} \Big[ \big( f(t) - f(s) \big)^2 \Big] \le C \left| t - s \right|^{1 + \delta}, \quad 0 \le s, t \le T
\end{equation*}](../../assets/latex/stochastic_differential_equations_4aee2794d002a4533abd2b23d204ba3e05dc398e.png)
Then the Riemann sum approximation for the stochastic integral converges in  to the same value for all
to the same value for all ![$\lambda \in [0, 1]$](../../assets/latex/stochastic_differential_equations_7cd670af2080b3c73aac2cd9f356000145119694.png) .
.
From the definition of a stochastic integral, we can make sense of a "noise differential equation", or a stochastic differential equation

with  being white noise.
being white noise.
The solution  then satisfies the integral equation
then satisfies the integral equation

which motivates the notation

since, in a way,

(sometimes you will actually see the Brownian motion (this definition for example) defined in this manner, e.g. lototsky2017stochastic)
Properties of Itô stochastic integral
Itô isometry
Let  be a Itô stochastic integral, then
be a Itô stochastic integral, then
![\begin{equation*}
\mathbb{E} \bigg[ \bigg( \int_{0}^{T} f(t) \ d W(t) \bigg)^2 \bigg] = \int_{0}^{T} \mathbb{E} \big[ \left| f(t) \right|^2 \big] \ dt
\end{equation*}](../../assets/latex/stochastic_differential_equations_fb938d7ae516ef815408e6ba427edacf5570c4b4.png)
From which it follows that for any square-integrable functions 
![\begin{equation*}
\mathbb{E} \bigg[ \bigg( \int_{0}^{T} h(t) \ d W(t) \int_{0}^{T} g(s) \ d W(s) \bigg) \bigg] = \mathbb{E} \bigg[ \int_{0}^{T} h(t) g(t) \ dt \bigg]
\end{equation*}](../../assets/latex/stochastic_differential_equations_4f628438f07e2d293292d9459a7513d58a6020e0.png)
![\begin{equation*}
\begin{split}
\mathbb{E} \bigg[ \bigg( \int_{0}^{T} f(t) + h(t) \ d W(t) \bigg)^2 \bigg]
&= \mathbb{E} \bigg[ \bigg( \int_{0}^{T} f(t) \ d W(t) \bigg)^2 + \bigg( \int_{0}^{T} h(t) \ d W(t) \bigg)^2 \\
& \qquad \quad + 2 \bigg( \int_{0}^{T} f(t) h(t) \ d W(t) \bigg) \bigg] \\
&= \int_{0}^{T} \mathbb{E} \big[ \left| f(t) \right|^2 \big] \ dt + \int_{0}^{T} \mathbb{E} \big[ \left| h(t) \right|^2 \big] \ d W(t) \\
& \qquad \quad + 2 \ \mathbb{E} \bigg[ \bigg( \int_{0}^{T} f(t) h(t) \ d W(t) \bigg) \bigg]
\end{split}
\end{equation*}](../../assets/latex/stochastic_differential_equations_e91e0d2442c044d62e44b072b27a636058360589.png)
but we also know that
![\begin{equation*}
\begin{split}
\mathbb{E} \bigg[ \bigg( \int_{0}^{T} f(t) + h(t) \ d W(t) \bigg)^2 \bigg] &= \int_{0}^{T} \mathbb{E} \big[ \left| f(t) + h(t) \right|^2 \big] \ dt \\
&= \int_{0}^{T} \mathbb{E} \big[ \left| f(t) \right|^2 \big] \ dt + \int_{0}^{T} \mathbb{E} \big[ \left| h(t) \right|^2 \big] \\
& \qquad + 2 \int_{0}^{T} \mathbb{E} \big[ \left| f(t) h(t) \right| \big] \ dt
\end{split}
\end{equation*}](../../assets/latex/stochastic_differential_equations_9f879b6173fae42516b10510f2ac63847b128e62.png)
Comparing with the equation above, we see that
![\begin{equation*}
\mathbb{E} \bigg[ \bigg( \int_{0}^{T} f(t) h(t) \ d W(t) \bigg) \bigg] = \mathbb{E} \bigg[ \int_{0}^{T} f(t) h(t) \ dt \bigg]
\end{equation*}](../../assets/latex/stochastic_differential_equations_c881fd770e7c6abd5046b9e697d22b2f0fe23aaa.png)
WHAT HAPPENED TO THE ABSOLUTE VALUE MATE?! Well, in the case where we are working with real functions, the Itô isometry is satisfied for  since it's equal to
since it's equal to  , which would give us the above expression.
, which would give us the above expression.
Martingale
For Itô stochastic integral we have
![\begin{equation*}
\mathbb{E} \bigg[ \int_{0}^{t} f(s) \ d W(s) \bigg] = 0
\end{equation*}](../../assets/latex/stochastic_differential_equations_e0b6cca05557ad2516584ec171f972e15a79ddff.png)
and
![\begin{equation*}
\mathbb{E} \bigg[ \int_{0}^{t} f(\ell) \ d W(\ell) \ \bigg| \ \mathscr{F}_s \bigg] = \int_{0}^{s} f(\ell) \ d W(\ell), \quad \forall t \ge s
\end{equation*}](../../assets/latex/stochastic_differential_equations_8fbada2b8f8a2d42a36cf0e9d18f4182125d905d.png)
where  denotes the filtration generated by
denotes the filtration generated by 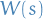 , hence the Itô integral is martingale.
, hence the Itô integral is martingale.
The quadratic variation of this martingale is
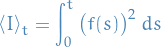
Solutions of SDEs
Consider SDEs of the form

where
A process  with continuous paths defined on the probability space
with continuous paths defined on the probability space 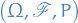 is called a strong solution to the SDE if:
is called a strong solution to the SDE if:
 is a.s. continuous and adapted to the filtration
is a.s. continuous and adapted to the filtration 
 and
and  a.s.
a.s.For every
 , the stochastic integral equation
, the stochastic integral equation
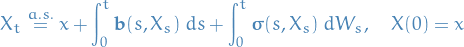
Let
satisfy the following conditions
There exists positive constant
 s.t. for all
s.t. for all  and
and ![$t \in [0, T]$](../../assets/latex/stochastic_differential_equations_a2d5fb401a604a95248d145edaa967973c136562.png)
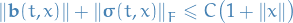
For all
 and
and ![$t \in [0, T]$](../../assets/latex/stochastic_differential_equations_a2d5fb401a604a95248d145edaa967973c136562.png) ,
,
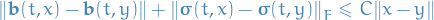
Furthermore, suppose that the initial condition  is a random variable independent of the Brownian motion
is a random variable independent of the Brownian motion  with
with
![\begin{equation*}
\mathbb{E} \big[ \norm{x}^2 \big] < \infty
\end{equation*}](../../assets/latex/stochastic_differential_equations_2d27c751e7fca7eb3452d0a396a0a7389e26a3d0.png)
Then the SDE

has a unique strong solution  with
with
![\begin{equation*}
\mathbb{E} \bigg[ \int_{0}^{t} \norm{X_s}^2 \ ds \bigg] < \infty, \quad \forall t \in [0, T]
\end{equation*}](../../assets/latex/stochastic_differential_equations_808b76e7e8694667082a16a47df91937c9f2dc5b.png)
where by unique we mean
![\begin{equation*}
X_t \overset{a.s.}{=} Y_t, \quad \forall t \in [0, T]
\end{equation*}](../../assets/latex/stochastic_differential_equations_c97999eabdc7c14abb1b33bea29438998a705a25.png)
for all possible solutions  and
and  .
.
Itô's Formula
Notation
Stuff
Consider Itô SDE

 is a diffusion process with drift
is a diffusion process with drift  and diffusion matrix
and diffusion matrix

The generator
 is then defined as
is then defined as
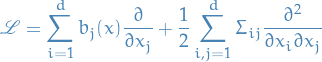
Assume that the conditions used in thm:unique-strong-solution hold.
Let  be the solution of
be the solution of

and let ![$V \in C^{1, 2} \big( [0, T] \times \mathbb{R}^d \big)$](../../assets/latex/stochastic_differential_equations_fed8860d87af42a04708c72ec34b91d85f59a2d5.png) . Then the process
. Then the process  satisfies
satisfies
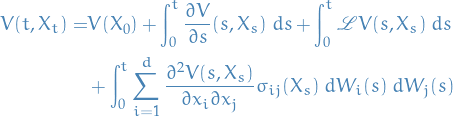
where the generator  is defined
is defined
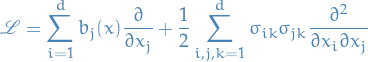
If we further assume that noise in different components are independent, i.e.
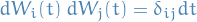
then  simplifies to
simplifies to
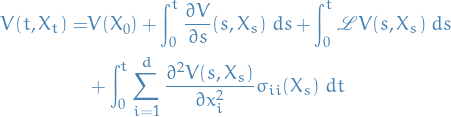
Finally, this can then be written in "differential form":
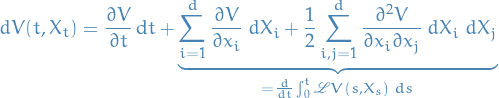
In pavliotis2014stochastic it is stated that the proof is very similar to the proof of the validity of the proof of the validity of the backward Kolmogorov equation for diffusion processes.
Feynman-Kac formula
- Itô's formula can be used to obtain a probabilistic description of solutions ot more general PDEs of parabolic type
Itô's formula can be used to obtain a probabilistic description of solutions of more general PDEs of parabolic type.
Let  be a diffusion process with
be a diffusion process with
- drift

- diffusion

- generator
 with
with 
and let
be bounded from below.
Then the function
![\begin{equation*}
u(x, t) = \mathbb{E} \bigg[ \exp \bigg( - \int_{0}^{t} V(X_s^x) \ ds \bigg) f(X_t^x) \bigg]
\end{equation*}](../../assets/latex/stochastic_differential_equations_9ecca43052b10d3a9f1ff5b0531aa145d13e6322.png)
is the solution to the IVP
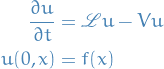
The representation  is then called the Feynman-Kac formula of the solution to the IVP.
is then called the Feynman-Kac formula of the solution to the IVP.
This is useful for theoretical analysis of IVP for parabolic PDEs of the form above, and for their numerical solution using Monte Carlo approaches.
Examples of solvable SDEs
Ornstein-Uhlenbeck process
Properties
- Mean-reverting
- Additive noise
Stuff

We observe that using Itô's formula
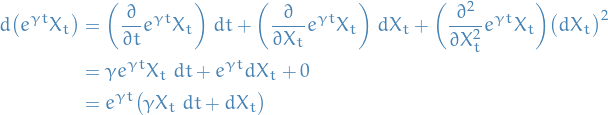
which from the Ornstein-Uhlenbeck equation we see that
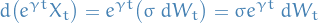
i.e.
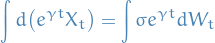
which gives us
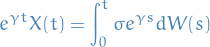
and thus
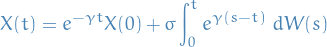
with  assumed to be non-random. This is the solution to the Ornstein-Uhlenbeck process.
assumed to be non-random. This is the solution to the Ornstein-Uhlenbeck process.
Further, we observe the following:
![\begin{equation*}
\mathbb{E} \big[ X(t) \big] = X_0 e^{- \gamma t}
\end{equation*}](../../assets/latex/stochastic_differential_equations_36ffd0487b3958b24eddc2a0dc4a0598723e7152.png)
since this is a Gaussian process. The covariance ew see
![\begin{equation*}
\begin{split}
& \mathbb{E} \big[ \big( X(t) - X_0 e^{- \gamma t} \big) \big( X(s) - X_0 e^{- \gamma t} \big) \big] \\
=\ & \mathbb{E} \bigg[ \bigg( \sigma \int_{0}^{t} e^{\gamma (t' - t)} \ dW(t') \bigg) \bigg( \sigma \int_{0}^{s} e^{\gamma (s' - s)} \ dW(s') \bigg) \bigg] \\
=\ & \sigma^2 \mathbb{E} \bigg[ \bigg( \int_{0}^{s} e^{\gamma (s' - t)} \ dW(s') \bigg) \bigg( \int_{0}^{s} e^{\gamma (s' - s)} \ dW(s') \bigg) \bigg( \int_{s}^{t} e^{\gamma (s' - t)} \ dW(s') \bigg) \bigg] \\
=\ & \sigma^2 \mathbb{E} \bigg[ \bigg( \int_{0}^{s} e^{\gamma (s' - t)} \ dW(s') \bigg) \bigg( \int_{0}^{s} e^{\gamma (s' - s)} \ dW(s') \bigg) \bigg( \int_{s}^{t} e^{\gamma (s' - t)} \ dW(s') \bigg) \bigg]
\end{split}
\end{equation*}](../../assets/latex/stochastic_differential_equations_df6f00842253cdc838d530799f1726b4b9d6bc33.png)
Assuming  , these are independent! Therefore
, these are independent! Therefore
![\begin{equation*}
\begin{split}
& \mathbb{E} \bigg[ \bigg( \int_{0}^{s} e^{\gamma (s' - t)} \ dW(s') \bigg) \bigg( \int_{0}^{s} e^{\gamma (s' - s)} \ dW(s') \bigg) \bigg( \int_{s}^{t} e^{\gamma (s' - t)} \ dW(s') \bigg) \bigg] \\
= \ & \mathbb{E} \bigg[ \bigg( \int_{0}^{s} e^{\gamma (s' - t)} \ dW(s') \bigg) \bigg( \int_{0}^{s} e^{\gamma (s' - s)} \ dW(s') \bigg) \bigg] \mathbb{E} \bigg[ \bigg( \int_{s}^{t} e^{\gamma (s' - t)} \ dW(s') \bigg) \bigg]
\end{split}
\end{equation*}](../../assets/latex/stochastic_differential_equations_9c7d537e76d7f15bbd3983434c708bbaaa0c4d32.png)
Using Itô isometry, the first factor becomes
![\begin{equation*}
\mathbb{E} \bigg[ \int_{0}^{s} e^{\gamma(2s' - t - s)} \ ds' \bigg] = \frac{1}{2 \gamma} \int_{0}^{s} e^{\tau} \ d \tau = \frac{1}{2 \gamma} \big( e^{s} - 1 \big)
\end{equation*}](../../assets/latex/stochastic_differential_equations_eebe9f22129cc8357346c735d42ae7518bf46662.png)
since
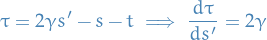
Langevin equation
Notation
 position of particle
position of particle velocity of particle
velocity of particle
Definition

Solution
Observe that the Langevin equation looks very similar to the Ornstein-Uhlenbeck process, but with  instead of
instead of  . We can write this as a system of two SDEs
. We can write this as a system of two SDEs
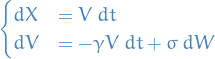
The expression for $d V $ is simply a OU process, and since this does not depend on  , we simply integrate as we did for the OU process giving us
, we simply integrate as we did for the OU process giving us
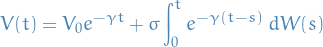
Subsituting into our expression for 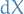 :
:
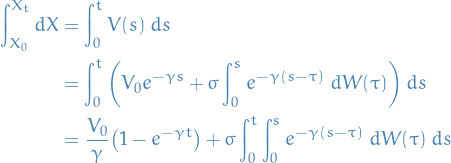
We notice that the integral here is what you call a "triangular" integral; we're integrating from  and integrating
and integrating  . We can therefore interchange the order of integration by integrating
. We can therefore interchange the order of integration by integrating  from
from  and the integrating
and the integrating  from
from  ! In doing so we get:
! In doing so we get:
![\begin{equation*}
\begin{split}
\int_{0}^{t} \int_{0}^{s} e^{- \gamma (s - \tau)} \dd{W(\tau)} \dd{s} &= \int_{0}^{t} \int_{\tau}^{t} e^{- \gamma(s - \tau)} \dd{s} \dd{W(\tau)} \\
&= \int_{0}^{t} - \frac{1}{\gamma} \big( e^{- \gamma (t - \tau)} - 1 \big) \dd{W(\tau)} \\
&= \frac{1}{\gamma} \bigg[ W(t) - \int_{0}^{t} e^{- \gamma (t - \tau)} \dd{W(\tau)} \bigg]
\end{split}
\end{equation*}](../../assets/latex/stochastic_differential_equations_eeff4eee75ee9fa340768570739b462467bd6ef9.png)
Hence the solution is given by
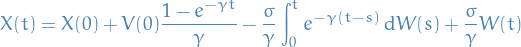
Geometric Brownian motion
The Geometric Brownian motion equation is given by
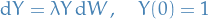
Brownian bridge
Consider the process  which satisfies the SDE
which satisfies the SDE
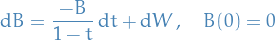
for  .
.
This is the definiting SDE for a Brownian bridge.
Solution
A random oscillator
The harmonic oscillator ODE 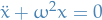 can be written as a system of ODEs:
can be written as a system of ODEs:
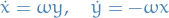
A stochastic version might be

where  is constant and the frequency is a white noise
is constant and the frequency is a white noise 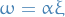 with
with  .
.
Solution
We can solve this by letting
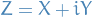
so

Then,

Hence,
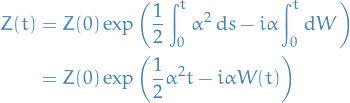
and thus

Stochastic Partial Differential Equations (rigorous)
Overview
This subsection are notes taken mostly from lototsky2017stochastic. This is quite a rigorous book which I find can be quite a useful supplement to the more "applied" descriptions of SDEs you'll find in most places.
I have found some of these more "formal" definitions to be provide insight:
- Brownian motion expressed as a sum over basis-elements multiplied with white noise in each term
- Definition of a "Gaussian process" as it is usually called, instead as a "Guassian field", such that each finite collection of random variables form a Gaussian vector.
Notation


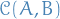 denotes the space of continuous mappings from metric space
denotes the space of continuous mappings from metric space 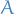 to metric space
to metric space 
- If
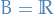 then we write
then we write 
- If
 is the collection of functions with
is the collection of functions with  continuous derivatives
continuous derivatives for
for  and
and  is the collection of functions with
is the collection of functions with  continuous derivatives s.t. derivatives of order
continuous derivatives s.t. derivatives of order  are Hölder continuous of order
are Hölder continuous of order  .
. is the collection of infinitely differentiable functions with compact support
is the collection of infinitely differentiable functions with compact support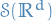 denotes the Schwartz space and
denotes the Schwartz space and  denotes the dual space (i.e. space of linear operators on
denotes the dual space (i.e. space of linear operators on 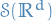 )
) denotes the partial derivatives of every order
denotes the partial derivatives of every order 
Partial derivatives:
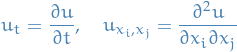
and
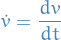
- Laplace operator is denoted by

 means
means
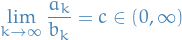
and if
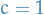 we will write
we will write 
 means
means
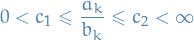
for all sufficiently larger
 .
.
 means that
means that  is a Gaussian rv. with mean
is a Gaussian rv. with mean  and variance
and variance 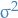
 or
or  are equations driven by Wiener process
are equations driven by Wiener process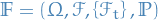
 is the sample space (i.e. underlying space of the measure space)
is the sample space (i.e. underlying space of the measure space) is the sigma-algebra (
is the sigma-algebra ( denotes the power set of
denotes the power set of  )
) is an increasing family of sub-algebras and
is an increasing family of sub-algebras and  is right-continuous (often called a filtration)
is right-continuous (often called a filtration) contains all
contains all  neglible sets, i.e.
neglible sets, i.e.  contains every subset of
contains every subset of  that is a subset of an element from
that is a subset of an element from  with
with  measure zero (i.e.
measure zero (i.e.  is complete)
is complete)
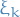 is an indep. std. Gaussian random variable
is an indep. std. Gaussian random variable
Definitions
A filtered probability space is given by

where the sigma-algebra  represents the information available up until time
represents the information available up until time  .
.
Let
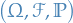 be a probability space
be a probability space be a filtration
be a filtration
A random process  is adapted if
is adapted if  is
is  .
.
This is equivalent to requiring that  for all
for all  .
.
Martingale
A square-integrable Martingale on  is a process
is a process  with values in
with values in 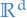 such that
such that
![\begin{equation*}
M(0) = 0, \quad \mathbb{E} \big[ \left| M(t) \right|^2 \big] < \infty
\end{equation*}](../../assets/latex/stochastic_differential_equations_9ffe6a53f3d1dc8249e53599704599571f3bae44.png)
and
![\begin{equation*}
\mathbb{E} \big[ M(t) \mid \mathcal{F}_s \big] = M(s), \quad \forall t \ge s \ge 0
\end{equation*}](../../assets/latex/stochastic_differential_equations_ebd69bb4c02cbe66f321212917ef7726f74fff4c.png)
A quadratic variation of a martingale 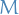 is the continuous non-decreasing real-valued process
is the continuous non-decreasing real-valued process  such that
such that

is a martingale.
A stopping (or Markov) time on  is a non-negative random variable
is a non-negative random variable  such that
such that

Introduction
If  is an orthonormal basis in
is an orthonormal basis in  , then
, then
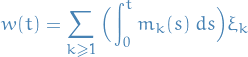
is a standard Brownian motion ; a Gaussian process with zero mean and covariance given by
![\begin{equation*}
\mathbb{E} [ w(t) w(s) ] = \min(t, s)
\end{equation*}](../../assets/latex/stochastic_differential_equations_119ad46a2e268146d2f1986e886b86adeea7cdea.png)
This definition of a standard Brownian motion does make a fair bit of sense.
It basically says that that a Brownian motion can be written as a sum of elements in the basis of the space, with each term being multiplied by some white noise.
The derivative of Brownian motion (though does not exist in the usual sense) is then defined

While the series certainly diverges, id oes define a random generalized function on  according to the rule
according to the rule
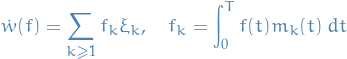
Consider
- a collection
 of indep. std. Brownian motions,
of indep. std. Brownian motions, ![$t \in [0, T]$](../../assets/latex/stochastic_differential_equations_a2d5fb401a604a95248d145edaa967973c136562.png)
orthonormal basis
 in the space
in the space  with
with

a d-dimensional hyper-cube.
For
 define
define
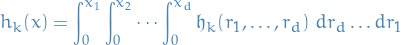
Then the process

is Gaussian,
![\begin{equation*}
\mathbb{E}[W(t,x)] = 0, \ \mathbb{E} \big[ W(t, x) W(s, y) \big] = \min(t, s) \prod_{k = 1}^d \min(x_k, y_k)
\end{equation*}](../../assets/latex/stochastic_differential_equations_ad1687b98946456fa75996d1242e479beb3c59ca.png)
We call this process  the Brownian sheet.
the Brownian sheet.
From Ex. 1.1.3 b) we have

are i.i.d. std. normal. From this we can define
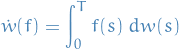
Writing
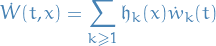
where 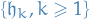 is an orthonormal basis in
is an orthonormal basis in 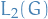 and
and  is an open set.
is an open set.
We call the process  the (Gaussian) space-time white noise. It is a random generalized function
the (Gaussian) space-time white noise. It is a random generalized function  :
:
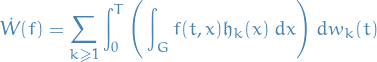
Sometimes, an alternative notation is used for 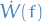 :
:
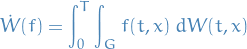
Unlike the Brownian sheet, space-time white noise  is defined on every domain
is defined on every domain  and not just on hyper-cuves
and not just on hyper-cuves 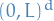 , as log as we can find an orthonormal basis
, as log as we can find an orthonormal basis 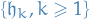 in
in 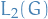 .
.
Integrating over 
Often see something like

e.g. in Ito's lemma, but what does this even mean?
Consider the integral above, which we then define as
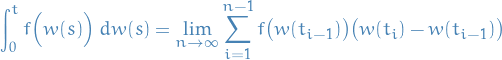
as we would do normally in the case of a Riemann-Stieltjes integral.
Now, observe that in the case of  being Brownian motion, each of these increments are well-defined!
being Brownian motion, each of these increments are well-defined!
Furthermore, considering a partial sum of the RHS in the above equation, we find that the partial sum converges to the infinite sum in the mean-squared sense.
This then means that the stochastic integral is a random variable, the samples of which depend on the individual realizations of the paths  !
!
Alternative description of Gaussian white noise
Zero-mean Gaussian process
 such that
such that
![\begin{equation*}
\mathbb{E} \big[ \dot{w}(t) \dot{w}(s) \big] = \delta(t - s)
\end{equation*}](../../assets/latex/stochastic_differential_equations_7e27abc40c28cc102d844ee3fb209b275cdd1d69.png)
where
 is the Dirac delta function.
is the Dirac delta function.
Similarily, we have
![\begin{equation*}
\mathbb{E} \big[ \dot{W}(t, x) \dot{W}(s, y) \big] = \delta(t - s) \delta(x - y)
\end{equation*}](../../assets/latex/stochastic_differential_equations_5e241f6536606487d8e8b936c3e010b756ea9fdb.png)
To construct noise that is white in time and coloured in space, take a sequence of non-negative numbers
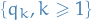 and define
and define
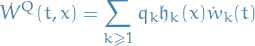
where
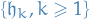 is an orthonormal basis in
is an orthonormal basis in 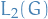 .
.
We say this noise is finite-dimensional if
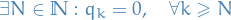
Useful Equalities
If  is a smooth function and
is a smooth function and  is a standard Brownian motion, then
is a standard Brownian motion, then
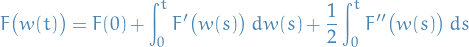
If  is a std. Brownian motion and
is a std. Brownian motion and  , an adapted process, then
, an adapted process, then
![\begin{equation*}
\mathbb{E} \Bigg[ \int_{0}^{T} f(t) \ dw(t) \Bigg]^2 = \int_{0}^{T} \mathbb{E} \big[ f^2(t) \big] \ dt
\end{equation*}](../../assets/latex/stochastic_differential_equations_8b5dd42d82b6de2c1f76d33d35465c776e01effe.png)
The Fourier transform is defined
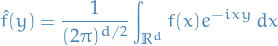
which is defined on the generalized functions from  by
by

for  and
and  . And the inverse Fourier transform is
. And the inverse Fourier transform is
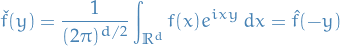
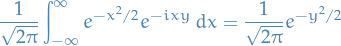
If 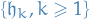 is an orthonormal basis in a Hilbert space
is an orthonormal basis in a Hilbert space  and
and  , then
, then
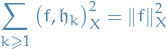
Plancherel's identity (or isometry of the Fourier transform) says that if  is a smooth function with compact support in
is a smooth function with compact support in 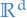 and
and
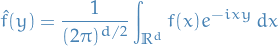
then
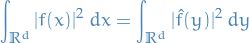
This result is essentially a continuum version of Parseval's identity.
Useful inequalities
Exercises
1.1.1
![\begin{equation*}
\mathbb{E} [w(t)w(s)] = \min(t,s)
\end{equation*}](../../assets/latex/stochastic_differential_equations_591d6076d829b731d7f3179accb14cfb5bea8d29.png)
Observe that
![\begin{equation*}
w(t) w(s) = \sum_{k}^{} \bigg[ \bigg( \int_{0}^{t} m_k(t') \ dt' \bigg) \xi_k \bigg] \bigg[ \bigg( \int_{0}^{s} m_k(s') \ ds' \bigg) \xi_k \bigg]
\end{equation*}](../../assets/latex/stochastic_differential_equations_c232059185a9dbadd873e9758a41f0411537d0a6.png)
since we're taking the product (see notation). Then, from the hint that  is the Fourier coefficient of the indicator function of the interval
is the Fourier coefficient of the indicator function of the interval ![$[0, t]$](../../assets/latex/stochastic_differential_equations_d5bfa804f666bf0df670b0537877972bb84945eb.png) , we make use of the Parseval identity:
, we make use of the Parseval identity:

where  denotes the k-th Fourier coefficient of the indicator function. Then
denotes the k-th Fourier coefficient of the indicator function. Then
![\begin{equation*}
\begin{split}
\mathbb{E}[w(t) w(s)] &= \sum_{k}^{} \big( I_t \big)_k \big( I_s \big)_k \mathbb{E}[\xi_k^2] \\
&= \sum_{k}^{} \big( I_t \big)_k \big( I_s \big)_k \\
&= I_t \ I_s \\
&= \min(t, s)
\end{split}
\end{equation*}](../../assets/latex/stochastic_differential_equations_235f44e5fca8101dfc16f9dcb03e03084a27604c.png)
since 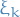 are all standard normal variables, hence
are all standard normal variables, hence ![$\text{Var}(\xi_k) = \mathbb{E}[\xi_k^2] = 1$](../../assets/latex/stochastic_differential_equations_84e9453ac96933dcaa2e36d51232b5e51a12aa37.png) .
.
I'm not entirely sure about that hint though? Are we not then assuming that the  is the basis? I mean, sure that's fine, but not specified anywhere as far as I can tell?
is the basis? I mean, sure that's fine, but not specified anywhere as far as I can tell?
Hooold, is inner-product same in any given basis? It is! (well, at least for finite bases, which this is not, but aight) Then it doesn't matter which basis we're working in, so we might as well use the basis of  and
and  .
.
1.1.2
Same procedure as in 1.1.1., but observing that we can separate  into a time- and position-dependent part, and again using the fact that
into a time- and position-dependent part, and again using the fact that

is just the Fourier coefficient of the indicator function on the range ![$[0, x_i]$](../../assets/latex/stochastic_differential_equations_4b4d7b652458d6943b1c96ba194271bbb7937a3a.png) in the i-th dimension.
in the i-th dimension.
Basic Ideas
Notation
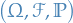 is a probability space
is a probability space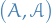 and
and 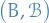 are two measurable spaces
are two measurable spaces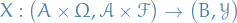 is a random function
is a random function- Random process refers to the case when
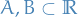
- Random field corresponds to when
 and
and 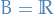 .
.
 and state space
and state space  denotes the
denotes the 
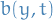


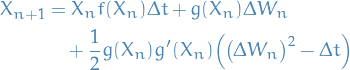
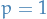 .
.
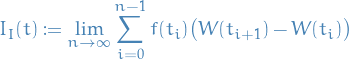
![$\mathbf{b}: [0, T] \times \mathbb{R}^d \to \mathbb{R}^d$](../../assets/latex/stochastic_differential_equations_9bfe6b358b9e1fbfe189485a8a952ec774c9685c.png)
![$\boldsymbol{\sigma}: [0, T] \times \mathbb{R}^{d} \to \mathbb{R}^{d \times m}$](../../assets/latex/stochastic_differential_equations_fd83ecd1f5fc746d9bf2c757c21fa4c09ee5dd6c.png)


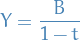
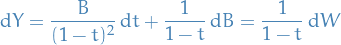
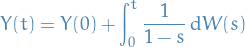
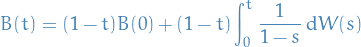
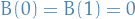 , we have
, we have