Measure theory
Table of Contents
Notation
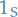 and
and 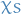 are used to denote the indicator or characteristic function
are used to denote the indicator or characteristic function
Definition
Motivation
The motivation behind defining such a thing is related to the Banach-Tarski paradox, which says that it is possible to decompose the 3-dimensional solid unit ball into finitely many pieces and, using only rotations and translations, reassemble the pieces into two solid balls each with the same volume as the original. The pieces in the decomposition, constructed using the axiom of choice, are non-measurable sets.
Informally, the axiom of choice, says that given a collecions of bins, each containing at least one object, it's possible to make a selection of exactly one object from each bin.
Measure space
If  is a set with the sigma-algebra
is a set with the sigma-algebra  and the measure
and the measure  , then we have a measure space .
, then we have a measure space .
Product measure
Given two measurable spaces and measures on them, one can obtain a product measurable space and a product measure on that space.
A product measure  is defined to be a measure on the measurable space
is defined to be a measure on the measurable space 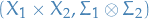 , where we've let
, where we've let  be the algebra on the Cartesian product
be the algebra on the Cartesian product  . This sigma-algebra is called the tensor-product sigma-algebra on the product space, which is defined
. This sigma-algebra is called the tensor-product sigma-algebra on the product space, which is defined
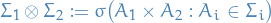
A product measure  is defined to be a measure on the measurable space
is defined to be a measure on the measurable space 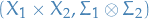 satisfying the property
satisfying the property

 and
and 
Let  be a sequence of extended real numbers.
be a sequence of extended real numbers.
The limit inferior is defined
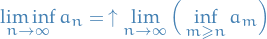
The limit supremum is defined
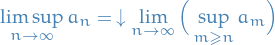
Premeasure
Given a space  , and a collection of sets
, and a collection of sets  is an algebra of sets on
is an algebra of sets on  if
if

- If
 , then
, then 
- If
 and
and  are in
are in  , then
, then 
Thus, a algebra of sets allow only finite unions, unlike σ-algebras where we allow countable unions.
Given a space  and an algebra
and an algebra  , a premeasure is a function
, a premeasure is a function ![$\lambda: \mathcal{A} \to [0, \infty]$](../../assets/latex/measure_theory_e17a0e8668dbd5fd1ed0e08c218ece154e7c2ed7.png) such that
such that

For every finite or countable collection of disjoint sets
 with
with  , if
, if 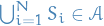 then
then
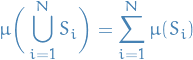
Observe that the last property says that IF this "possibly large" union is in the algebra, THEN that sum exists.
A premeasure space is a triple 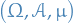 where
where  is a space,
is a space,  is an algebra, and a premeasure
is an algebra, and a premeasure  .
.
Complete measure
A complete measure (or, more precisely, a complete measure space ) is a measure space in which every subset of every null set is measurable (having measure zero).
More formally, 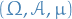 is complete if and only if
is complete if and only if

If 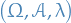 is a premeasure space, then there is a complete measure space
is a premeasure space, then there is a complete measure space 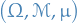 such that
such that

 we have
we have 
If  is σ-finite, then
is σ-finite, then  is the only measure on
is the only measure on  that is equal to
that is equal to  on
on  .
.
Atomic measure
Let  be a measure space.
be a measure space.
Then a set  is called an atom if
is called an atom if
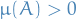
and

A measure  which has no atoms is called non-atomic or diffuse
which has no atoms is called non-atomic or diffuse
In other words, a measure  is non-atomic if for any measurable set
is non-atomic if for any measurable set 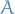 with
with 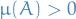 , there exists a measurable subset
, there exists a measurable subset  s.t.
s.t.
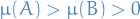
π-system
Let  be any set. A family
be any set. A family  of subsets of
of subsets of  is called a π-system if
is called a π-system if

If
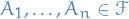 , then
, then

So this is an even weaker notion than being an (Boolean) algebra. We introduce it because it's sufficient to prove uniqueness of measures:
Theorems
Jensen's inequality
Let
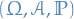 be a probability space
be a probability space be random variable
be random variable![$c: \mathbb{R} \to (-\infty, \infty]$](../../assets/latex/measure_theory_0fbf01fc0b204736d63b072e13cefceee1e07280.png) be a convex function
Then
be a convex function
Then  is the supremum of a sequence of affine functions
is the supremum of a sequence of affine functions
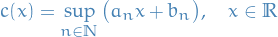
for
 , with
, with  .
.
Then ![$\mathbb{E}[c(X)]$](../../assets/latex/measure_theory_a9eba1896bb741b60c40f7b709c13a7dfdf79cbf.png) is well-defined, and
is well-defined, and
![\begin{equation*}
\mathbb{E}[c(X)] \overset{a.s.}{\ge} a_n \mathbb{E}[X] + b_n
\end{equation*}](../../assets/latex/measure_theory_27722a1c52318e0443a664830effa0bb1a3503a3.png)
Taking the supremum over  in this inequality, we obtain
in this inequality, we obtain
![\begin{equation*}
\mathbb{E}[c(X)] \ge c \big( \mathbb{E}[X] \big)
\end{equation*}](../../assets/latex/measure_theory_8c3280bc7d5e2fce41ec6d17771166c73ae27475.png)
![$c: \mathbb{R} \to (-\infty, \infty]$](../../assets/latex/measure_theory_0fbf01fc0b204736d63b072e13cefceee1e07280.png) be a convex function
Then
be a convex function
Then  is the supremum of a sequence of affine functions
is the supremum of a sequence of affine functions
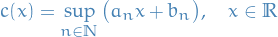
Suppose  is convex, then for each point
is convex, then for each point  there exists an affine function
there exists an affine function  s.t.
s.t.
- the line
 corresponding to
corresponding to  passes through
passes through 
- the graph of
 lies entirely above
lies entirely above 
Let  be the set of all such functions. We have
be the set of all such functions. We have
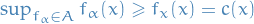 because
because  passes through the point
passes through the point 
 beacuse all
beacuse all  lies below
lies below 
Hence
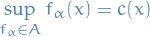
(note this is for each  , i.e. pointwise).
, i.e. pointwise).
Sobolev space
Notation
 is an open subset of
is an open subset of 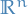
 denotes a infinitively differentiable function
denotes a infinitively differentiable function  with compact support
with compact support is a multi-index of order
is a multi-index of order  , i.e.
, i.e.
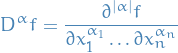
Definition
Vector space of functions equipped with a norm that is a combination of  norms of the function itself and its derivatoves to a given order.
norms of the function itself and its derivatoves to a given order.
Intuitively, a Sobolev space is a space of functions with sufficiently many derivatives for some application domain, e.g. PDEs, and equipped with a norm that measures both size and regularity of a function.
The Sobolev space spaces  combine the concepts of weak differentiability and Lebesgue norms (i.e.
combine the concepts of weak differentiability and Lebesgue norms (i.e.  spaces).
spaces).
For a proper definition for different cases of dimension of the space  , have a look at Wikipedia.
, have a look at Wikipedia.
Motivation
Integration by parst yields that for every  where
where  , and for all infinitively differentiable functions with compact support
, and for all infinitively differentiable functions with compact support  :
:
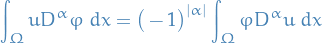
Observe that LHS only makes sense if we assume  to be locally integrable. If there exists a locally integrable function
to be locally integrable. If there exists a locally integrable function  , such that
, such that
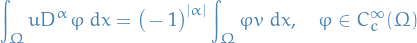
we call  the weak
the weak  -th partial derivative of
-th partial derivative of  . If this exists, then it is uniquely defined almost everywhere, and thus it is uniquely determined as an element of a Lebesgue space (i.e.
. If this exists, then it is uniquely defined almost everywhere, and thus it is uniquely determined as an element of a Lebesgue space (i.e.  function space).
function space).
On the other hand, if  , then the classical and the weak derivative coincide!
, then the classical and the weak derivative coincide!
Thus, if 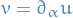 , we may denote it by
, we may denote it by  .
.
Example
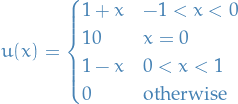
is not continuous at zero, and not differentiable at −1, 0, or 1. Yet the function
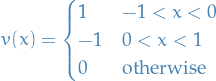
satisfies the definition of being the weak derivative of  , which then qualifies as being in the Sobolev space
, which then qualifies as being in the Sobolev space  (for any allowed
(for any allowed 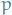 ).
).
Lebesgue measure
Notation
 denotes the collection of all measurable sets
denotes the collection of all measurable sets
Stuff
Given a subset  , with the length of a closed interval
, with the length of a closed interval ![$I = [a,b]$](../../assets/latex/measure_theory_3fdf3f4bf882725c6261a1b413e5bc0b103e1281.png) given by
given by  , the Lebesgue outer measure
, the Lebesgue outer measure  is defined as
is defined as

Lebesgue outer-measure has the following properties:
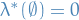 Idea: Cover by
Idea: Cover by 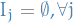 .
.(Monotinicy)
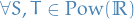 if
if  , then
, then

Idea: a cover of
 is a cover of
is a cover of  .
.
(Countable subadditivity) For every set
 and every sequence of sets
and every sequence of sets  if
if  then
then
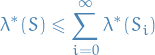
Idea: construct a cover of each
 ,
,  such that
such that  :
:
- Every point in
 is in one of the
is in one of the 
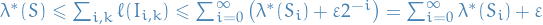
- Every point in
Q: Is it possible for every  to find a cover
to find a cover 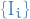 such that
such that  ?
A: No. Consider
?
A: No. Consider  . Given
. Given  , consider
, consider 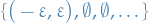 .
This is a cover of
.
This is a cover of  so
so  .
If
.
If 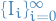 is a cover by open intervals of
is a cover by open intervals of  , then there is at least one
, then there is at least one  such that
such that  is a nonempty open interval, so it has a strictly positive lenght, and
is a nonempty open interval, so it has a strictly positive lenght, and
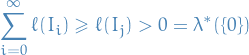
If  , then
, then
![\begin{equation*}
\lambda^* \big( [a, b] \big) = \lambda^*([a, b)) = \lambda^* \big( (a, b] \big) = \lambda^* \big( (a, b) \big)
\end{equation*}](../../assets/latex/measure_theory_e6c6a70aa01d16ddfce344bbaedabbd1746e51f5.png)
Idea: ![$\big( a ,b \big) \subseteq [a, b]$](../../assets/latex/measure_theory_c7ddd35e2c2b0a06fa21ecb3622aa3c7a90f9cd9.png) , so
, so ![$\lambda^* \big( (a, b) \big) \le \lambda^* \big( [a, b] \big)$](../../assets/latex/measure_theory_a246293098d05d0199b421bc104c358809bd3568.png) .
For reverse, cover
.
For reverse, cover 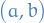 by intervals giving a sum within
by intervals giving a sum within  .
Then cover
.
Then cover  and
and  by intervals of length
by intervals of length  .
Put the 2 new sets at at the start of the sequence, to get a cover of
.
Put the 2 new sets at at the start of the sequence, to get a cover of ![$[a, b]$](../../assets/latex/measure_theory_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) , and sum of the lengths is at most
, and sum of the lengths is at most 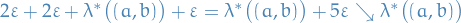 . Hence,
. Hence,
![\begin{equation*}
\lambda^* \big( (a, b) \big) \le \lambda^* \big( [a, b] \big) \text{ and } \lambda^* \big( [a, b] \big) \le \lambda^* \big( (a, b) \big)
\end{equation*}](../../assets/latex/measure_theory_e07a5a74202cf48119137eaee61040e633e6ac87.png)
If  is an open interval, then
is an open interval, then  .
.
Idea: lower bound from  .
Only bounded nonempty intervals are interesting.
Take the closure to get a compact set. Given a countable cover by open intervals, reduce to a finite subcover.
Then arrange a finite collection of intervals in something like increasing order, possibly dropping unnecessary sets.
Call these new intervals
.
Only bounded nonempty intervals are interesting.
Take the closure to get a compact set. Given a countable cover by open intervals, reduce to a finite subcover.
Then arrange a finite collection of intervals in something like increasing order, possibly dropping unnecessary sets.
Call these new intervals  and let
and let 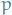 be the number of such intervals, and such that
be the number of such intervals, and such that

i.e. left-most interval cover the starting-point, and right-most interval cover the end-point. Then
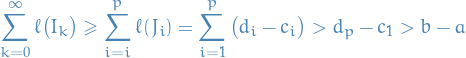
Taking the infimum,

The Lebesgue measure is then defined on the Lebesgue sigma-algebra, which is the collection of all the sets  which satisfy the condition that, for every
which satisfy the condition that, for every 

For any set in the Lebesgue sigma-algrebra, its Lebesgue measure is given by its Lebesgue outer measure  .
.
IMPORTANT!!! This is not necessarily related to the Lebesgue integral! It CAN be be, but the integral is more general than JUST over some Lebesgue measure.
Intuition
- First part of definition states that the subset
 is reduced to its outer measure by coverage by sets of closed intervals
is reduced to its outer measure by coverage by sets of closed intervals - Each set of intervals
 covers
covers  in the sense that when the intervals are combined together by union, they contain
in the sense that when the intervals are combined together by union, they contain 
- Total length of any covering interval set can easily overestimate the measure of
 , because
, because  is a subset of the union of the intervals, and so the intervals include points which are not in
is a subset of the union of the intervals, and so the intervals include points which are not in 
Lebesgue outer measure emerges as the greatest lower bound (infimum) of the lengths from among all possible such sets. Intuitively, it is the total length of those interval sets which fit  most tightly and do not overlap.
most tightly and do not overlap.
In my own words: Lebesgue outer measure is smallest sum of the lengths of subintervals  s.t. the union of these subintervals
s.t. the union of these subintervals  completely "covers" (i.e. are equivalent to)
completely "covers" (i.e. are equivalent to)  .
.
If you take an a real interval ![$I = [a, b]$](../../assets/latex/measure_theory_f5678fa616e44d479ff19a74dbf6956a9abbbf8c.png) , then the Lebesge outer measure is simply
, then the Lebesge outer measure is simply  .
.
Properties
Notation
For
 and
and  , we let
, we let

Stuff
The collection of Lebesgue measurable sets is a sigma-algebra.
Easy to see
 is in this collection:
is in this collection:

Closed under complements is clear: let
 be Lebesgue measurable, then
be Lebesgue measurable, then
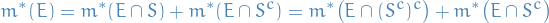
hence this is also true for
 , and so
, and so  is Lebesgue measurable.
is Lebesgue measurable.
- Closed under countable unions:
Finite case:
 .
Consider
.
Consider  both Lebesgue measurable and some set
both Lebesgue measurable and some set  .
Since
.
Since 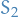 is L. measurable:
is L. measurable:

Since
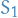 is L. measurable:
is L. measurable:

which allows us to rewrite the above equation for
 :
:

Observe that

By subadditivity:

Hence,

Then this follows for all finite cases by induction.
Countable disjoint case: Let
 , and
, and  . Further, let
. Further, let  .
.

Hence
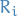 is L. measurable. Thus,
is L. measurable. Thus,

Since the
 are disjoint
are disjoint  and
and  :
:
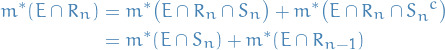
Let
 and note that
and note that  .
Thus, by indiction
.
Thus, by indiction
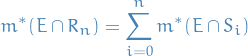
Thus,

Taking
 :
:
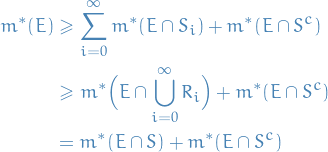
Thus,
 is L. measurable if the
is L. measurable if the  are disjoint and L. measurable!
are disjoint and L. measurable!
- Countable (not-necessarily-disjoint) case:
If
 are not disjoint, let
are not disjoint, let  and let
and let  , which gives a sequence of disjoint sets, hence the above proof applies.
, which gives a sequence of disjoint sets, hence the above proof applies.
Every open interval is Lebesgue measurable, and the Borel sigma-algebra is a subset of the sigma-algebra of Lebesgue measurable sets.
Want to prove measurability of intervals of the form  .
.
Idea:
- split any set
 into the left and right part
into the left and right part - split any cover in the same way
- extend covers by
 to make them open
to make them open
 is a measure space, and for al intervals
is a measure space, and for al intervals  , the measure is the length.
, the measure is the length.
Cantor set
Define
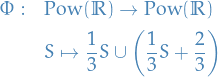
For  , with
, with  being identity, and
being identity, and

Let ![$E_0 = [0, 1]$](../../assets/latex/measure_theory_2841c9b582f2d0607515b04b91c33a1a58903197.png) and
and  . Then the Cantor set is defined
. Then the Cantor set is defined
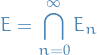
The Cantor set has a Lebesgue measure zero.
We make the following observations:
- Scaled and shifted closed sets are closed
 is a finite union of closed intervals and so is in the Borel sigma-algebra
is a finite union of closed intervals and so is in the Borel sigma-algebra- σ-algebras are closed under countable intersections, hence Cantor set is in the Borel σ-algebra
- Finally, Borel σ-algebra is a subset of Lebesgue measurable sets, hence the Cantor set is Lebesuge measurable!
Since Lebesgue measure satisfy  for any Lebesgue measurable set
for any Lebesgue measurable set  with finite measure and any
with finite measure and any  with
with  . Since Lebesgue measure is subadditive, we have for any
. Since Lebesgue measure is subadditive, we have for any 

Since  , by induction, it follows that
, by induction, it follows that
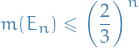
Taking the infimum of over  , we have that the Cantor set has measure zero:
, we have that the Cantor set has measure zero:
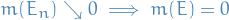
Cardinality of the Cantor set
Let ![$x \in [0, 1]$](../../assets/latex/measure_theory_1abcf6a6ba0996351c652ec55b2a137f25774cfc.png) .
.
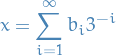
The terniary expansion is a sequence  with
with 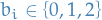 such that
such that
The Cantor set  is uncountable.
is uncountable.
We observe that if the first  elements of the expansion for
elements of the expansion for  are in
are in 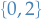 , then
, then  . But importantly, observe that some numbers have more than one terniary expansion, i.e.
. But importantly, observe that some numbers have more than one terniary expansion, i.e.

in the terniary expansion. One can show that a number  if and only if
if and only if  has a terniary expansion with no 1 digits. Hence, the Cantor set
has a terniary expansion with no 1 digits. Hence, the Cantor set  is uncountable!
is uncountable!
One can see that  if and only if terniary expansion with no 1 digits, since such an
if and only if terniary expansion with no 1 digits, since such an  would land in the "gaps" created by the construction of the Cantor set.
would land in the "gaps" created by the construction of the Cantor set.
Uncountable Lebesgue measurable set
There exists uncountable Lebesgue measurable sets.
Menger sponge
- Generalization of Cantor set to

Vitali sets
Let  if and only if
if and only if 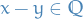 .
.
- There are uncountable many equivalence classes, with each equivalence class being countable (as a set).
- By axiom of choice, we can pick one element from each equivalence class.
- Can assume each representative picked is in
![$[0, 1]$](../../assets/latex/measure_theory_68c8fa38d960e53d4308cbf1e65d04c66a554817.png) , and this set we denote
, and this set we denote 
Suppose, for the sake of contradiction, that  is measurable.
is measurable.
Observe if ![$x \in [0, 1]$](../../assets/latex/measure_theory_1abcf6a6ba0996351c652ec55b2a137f25774cfc.png) , then there is a
, then there is a  and
and  s.t.
s.t. ![$q \in [-1, 1]$](../../assets/latex/measure_theory_e2a141e95f622cba27e76a7586a7befe39020eda.png) , i.e.
, i.e.
![\begin{equation*}
[0, 1] \subseteq \bigcup_{q \in [-1, 1] \cap \mathbb{Q}}^{} \Big( R + q \Big) \subseteq [-1, 2]
\end{equation*}](../../assets/latex/measure_theory_f79853c87366563f923b51372436ae537e0d78ed.png)
Then, by countable additivity
![\begin{equation*}
\begin{split}
m([0, 1]) &\le m \bigg( \bigcup_{q \in [-1, 1] \cap \mathbb{Q}}^{} R + q \bigg) \le m \big( [-1, 2] \big) = 3 \\
m([0, 1]) &\le \sum_{q \in [-1, 1] \cap \mathbb{Q}}^{} m (R + q) \le 3 \\
m([0, 1]) &\le \sum_{q \in [-1, 1] \cap \mathbb{Q}}^{} m (R) \le 3
\end{split}
\end{equation*}](../../assets/latex/measure_theory_10cc4bf4c4028ae61e6bec3e9a6df729d34e627e.png)
where we've used
![\begin{equation*}
m \bigg( \bigcup_{q \in [-1, 1] \cap \mathbb{Q}}^{} R + q \bigg) = \sum_{q \in [-1, 1] \cap \mathbb{Q}}^{} m (R + q) = \sum_{q \in [-1, 1] \cap \mathbb{Q}}^{} m (R)
\end{equation*}](../../assets/latex/measure_theory_4c878026d358487ad76ea895c4e45d05d969e74a.png)
Hence, we have our contradiction and so this set, the Vitali set, is not measurable!
There exists a subset of  that is not measurable wrt. Lebesgue measure.
that is not measurable wrt. Lebesgue measure.
Lebesgue Integral
The Lebesgue integral of a function  over a measure space
over a measure space  is written
is written

which means we're taking the integral wrt. the measure  .
.

Special case: non-negative real-valued function
Suppose that  is a non-negative real-valued function.
is a non-negative real-valued function.
Using the "partitioning of range of  " philosophy, the integral of
" philosophy, the integral of  should be the sum over
should be the sum over  of the elementary area contained in the thin horizontal strip between
of the elementary area contained in the thin horizontal strip between 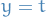 and
and  , which is just
, which is just
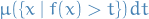
Letting

The Lebesgue integral of  is then defined by
is then defined by
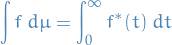
where the integral on the right is an ordinary improper Riemann integral. For the set of measurable functions, this defines the Lebesgue integral.
Radon measure
- Hard to find a good notion of measure on a topological space that is compatible with the topology in some sense
- One way is to define a measure on the Borel set of the topological space
Let  be a measure on the sigma-algebra of Borel sets of a Hausdorff topological space
be a measure on the sigma-algebra of Borel sets of a Hausdorff topological space  .
.
 is called inner regular or tight if, for any Borel set
is called inner regular or tight if, for any Borel set  ,
,  is the supremum of
is the supremum of 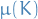 over all compact subsets of
over all compact subsets of  of
of  , i.e.
, i.e.

where
 denotes the compact interior, i.e. union of all compact subsets
denotes the compact interior, i.e. union of all compact subsets  .
.
 is called outer regular if, for any Borel set
is called outer regular if, for any Borel set  ,
,  is the infimum of
is the infimum of  over all open sets
over all open sets  containing
containing  , i.e.
, i.e.

where
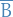 denotes the closure of
denotes the closure of  .
.
 is called locally finite if every point of
is called locally finite if every point of  has a neighborhood
has a neighborhood  for which
for which  is finite (if
is finite (if  is locally finite, then it follows that
is locally finite, then it follows that  is finite on compact sets)
is finite on compact sets)
The measure  is called a Radon measure if it is inner regular and locally finite.
is called a Radon measure if it is inner regular and locally finite.
Suppose  and
and  are two
are two  measures on a measures on a measurable space
measures on a measures on a measurable space 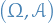 and
and  is absolutely continuous wrt.
is absolutely continuous wrt.  .
.
Then there exists a non-negative, measurable function  on
on  such that
such that

The function  is called the density or Radon-Nikodym derivative of
is called the density or Radon-Nikodym derivative of  wrt.
wrt.  .
.
If a Radon-Nikodym derivative of  wrt.
wrt.  exists, then
exists, then  denotes the equivalence class of measurable functions that are Radon-Nikodym derivatives of
denotes the equivalence class of measurable functions that are Radon-Nikodym derivatives of  wrt.
wrt.  .
.
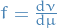 is often used to denote
is often used to denote  , i.e.
, i.e.  is just in the equivalence class of measurable functions such that this is the case.
is just in the equivalence class of measurable functions such that this is the case.
This comes from the fact that we have
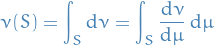
Suppose  and
and 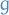 are Radon-Nikodym derivatives of
are Radon-Nikodym derivatives of  wrt.
wrt.  iff
iff  .
.
The δ measure cannot have a Radon-Nikodym derivative since integrating  gives us zero for all measurable functions.
gives us zero for all measurable functions.
Continuity of measure
Suppose  and
and  are two sigma-finite measures on a measure space
are two sigma-finite measures on a measure space 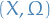 .
.
Then we say that  is absolutely continuous wrt.
is absolutely continuous wrt.  if
if

We say that  and
and  are equivalent if each measure is absolutely continuous wrt. to the other.
are equivalent if each measure is absolutely continuous wrt. to the other.
Density
Suppose  and
and  are two sigma-finite measures on a measure space
are two sigma-finite measures on a measure space 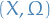 and that
and that  is absolutely continuous wrt.
is absolutely continuous wrt.  . Then there exists a non-negative, measurable function
. Then there exists a non-negative, measurable function  on
on  such that
such that
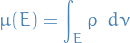
Measure-preserving transformation
 is a measure-preserving transformation is a transformation on the measure-space
is a measure-preserving transformation is a transformation on the measure-space  if
if
Measure
A measure on a set is a systematic way of defining a number to each subset of that set, intuitively interpreted as size.
In this sense, a measure is a generalization of the concepts of length, area, volume, etc.
Formally, let  be a
be a 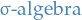 of subsets of
of subsets of  .
.
Suppose ![$\mu: \mathcal{A} \to [0, \infty]$](../../assets/latex/measure_theory_beef385f676dedc4e7697f3bc64effffd9d7d3aa.png) is a function. Then
is a function. Then  is a measure if
is a measure if

Whenever
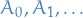 are pairwise disjoint subsets of
are pairwise disjoint subsets of  in
in  , then
, then
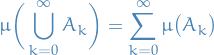
- Called σ-additivity or sub-additivity
Properties
Let 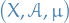 be a measure space, and
be a measure space, and 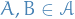 such that
such that  .
.
Then  .
.
Let

Then 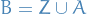 , and by finite additivity property of a measure:
, and by finite additivity property of a measure:

since  by definition of a measure.
by definition of a measure.
If 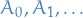 are
are  subsets of
subsets of  , then
, then
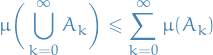
We know for a sequence of disjoint sets  we have
we have
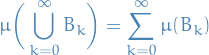
So we just let
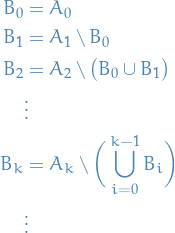
Then,
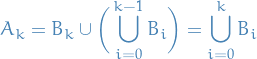
Thus,
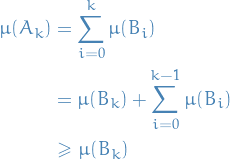
Concluding our proof!
Let 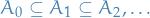 be an increasing sequence of measurable sets.
be an increasing sequence of measurable sets.
Then
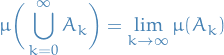
Let  be sets from some
be sets from some 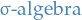
 .
.
If  , then
, then
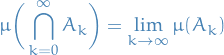
Examples of measures
Let
 be a space
be a space
The δ-measure (at  ) is
) is
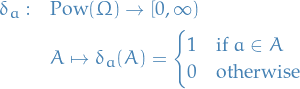
Sigma-algebra
Definition
Let  be some set, and let
be some set, and let 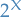 be its power set. Then the subset
be its power set. Then the subset  is a called a σ-algebra on
is a called a σ-algebra on  if it satisfies the following three properties:
if it satisfies the following three properties:

 is closed under complement: if
is closed under complement: if 
 is closed under countable unions: if
is closed under countable unions: if 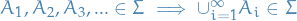
These properties also imply the following:

 is closed under countable intersections: if
is closed under countable intersections: if 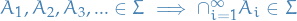
Generated σ-algebras
Given a space  and a collection of subsets
and a collection of subsets 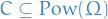 , the σ-algebra generated by
, the σ-algebra generated by  , denoted
, denoted  , is defined to be the intersection of all σ-algebras on
, is defined to be the intersection of all σ-algebras on  that contain
that contain  , i.e.
, i.e.
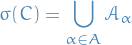
where

Let 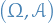 be a measurable space and
be a measurable space and  a function from some space
a function from some space  to
to  .
.
The σ-algebra generated by  is
is
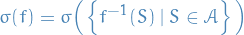
Observe that though this is similar to σ-algebra generated by MEASURABLE function, the definition differs in a sense that the preimage does not have to be measurable. In particular, the σ-algebra generated by a measurable function can be defined as above, where 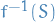 is measurable by definition of
is measurable by definition of  being a measurable function, hence corresponding exactly to the other definition.
being a measurable function, hence corresponding exactly to the other definition.
Let 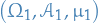 and
and 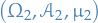 be measure spaces and
be measure spaces and 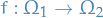 a measurable function.
a measurable function.
The σ-algebra generated by  is
is

Let  be a space.
be a space.
If  is a collection of σ-algebras, then
is a collection of σ-algebras, then  is also a σ-algebra.
is also a σ-algebra.
σ-finite
A measure or premeasure space 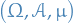 is finite if
is finite if  .
.
A measure  on a measure space
on a measure space 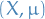 is said to be sigma-finite if
is said to be sigma-finite if  can be written as a countable union of measurable sets of finite measure.
can be written as a countable union of measurable sets of finite measure.
Example: counting measure on uncountable set is not σ-finite
Let  be a space.
be a space.
The counting measure is defined to be 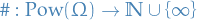 such that
such that

On any uncountable set, the counting measure is not σ-finite, since if a set has finite counting measure it has countably many elements, and a countable union of finite sets is countable.
Properties
Let  be a
be a 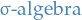 of subsets of a set
of subsets of a set  . Then
. Then
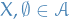
If
 , then
, then

- If
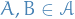 then
then 
Borel sigma-algebra
Any set in a topological space that can be formed from the open sets through the operations of:
- countable union
- countable intersection
- complement
is called a Borel set.
Thus, for some topological space  , the collection of all Borel sets on
, the collection of all Borel sets on  forms a σ-algebra, called the Borel algebra or Borel σ-algebra .
forms a σ-algebra, called the Borel algebra or Borel σ-algebra .
More compactly, the Borel σ-algebra on  is
is

where 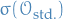 is the σ-algebra generated by the standard topology on
is the σ-algebra generated by the standard topology on  .
.
Borel sets are important in measure theory, since any measure defined on the open sets of a space, or on the closed sets of a space, must also be defined on all Borel sets of that space.
Any measure defined on the Borel sets is called a Borel measure.
Lebesgue sigma-algebra
Basically the same as the Borel sigma-algebra but the Lebesgue sigma-algebra forms a complete measure.
Note to self
Suppose we have a Lebesgue mesaure on the real line, with measure space 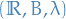 .
.
Suppose that 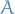 is non-measurable subset of the real line, such as the Vitali set. Then the
is non-measurable subset of the real line, such as the Vitali set. Then the 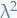 measure of
measure of  is not defined, but
is not defined, but

and this larger set (  ) does have
) does have 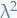 measure zero, i.e. it's not complete !
measure zero, i.e. it's not complete !
Motivation
Suppose we have constructed Lebesgue measure on the real line: denote this measure space by 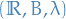 . We now wish to construct some two-dimensional Lebesgue measure
. We now wish to construct some two-dimensional Lebesgue measure 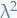 on the plane
on the plane  as a product measure.
as a product measure.
Naïvely, we could take the sigma-algebra on  to be
to be  , the smallest sigma-algebra containing all measureable "rectangles"
, the smallest sigma-algebra containing all measureable "rectangles"  for
for  .
.
While this approach does define a measure space, it has a flaw: since every singleton set has one-dimensional Lebesgue measure zero,

for any subset of  .
.
What follows is the important part!
However, suppose that 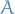 is non-measureable subset of the real line, such as the Vitali set. Then the
is non-measureable subset of the real line, such as the Vitali set. Then the 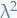 measure of
measure of  is not defined (since we just supposed that
is not defined (since we just supposed that 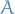 is non-measurable), but
is non-measurable), but

and this larger set (  ) does have
) does have 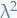 measure zero, i.e. it's not complete !
measure zero, i.e. it's not complete !
Construction
Given a (possible incomplete) measure space  , there is an extension
, there is an extension 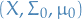 of this measure space that is complete .
of this measure space that is complete .
The smallest such extension (i.e. the smallest sigma-algebra  ) is called the completion of the measure space.
) is called the completion of the measure space.
It can be constructed as follows:
- Let
 be the set of all
be the set of all  measure zero subsets of
measure zero subsets of  (intuitively, those elements of
(intuitively, those elements of  that are not already in
that are not already in  are the ones preventing completeness from holding true)
are the ones preventing completeness from holding true) - Let
 be the sigma-algebra generated by
be the sigma-algebra generated by  and
and  (i.e. the smallest sigma-algreba that contains every element of
(i.e. the smallest sigma-algreba that contains every element of  and of
and of  )
)  has an extension to
has an extension to  (which is unique if
(which is unique if  is sigma-finite), called the outer measure of
is sigma-finite), called the outer measure of  , given by the infimum
, given by the infimum

Then 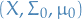 is a complete measure space, and is the completion of
is a complete measure space, and is the completion of  .
.
What we're saying here is:
- For the "multi-dimensional" case we need to take into account the zero-elements in the resulting sigma-algebra due the product between the 1D zero-element and some element NOT in our original sigma-algebra
- The above point means that we do NOT necessarily get completeness, despite the sigma-algebras defined on the sets individually prior to taking the Cartesian product being complete
- To "fix" this, we construct a outer measure
 on the sigma-algebra where we have included all those zero-elements which are "missed" by the naïve approach,
on the sigma-algebra where we have included all those zero-elements which are "missed" by the naïve approach, 
Measurable functions
Let 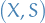 and
and 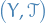 be measurable spaces.
be measurable spaces.
A function  is a measurable function if
is a measurable function if
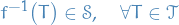
where  denotes the preimage of the
denotes the preimage of the  for the measurable set
for the measurable set  .
.
Let  .
.
We define the indicator function of  to be the function
to be the function 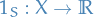 given by
given by
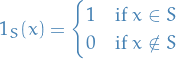
Let  . Then
. Then  is measurable if and only if
is measurable if and only if  .
.
Let 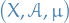 be a measure space or a probability space.
be a measure space or a probability space.
Let 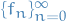 be a sequence of measurable functions.
be a sequence of measurable functions.
- For each
 , the function
, the function  is measurable
is measurable - The function
 is measurable
is measurable - Thus, if
 converge pointwise,
converge pointwise,  is measurable.
is measurable.
Let  be a measurable space, and let
be a measurable space, and let ![$f: X \to \big[ - \infty, \infty \big]$](../../assets/latex/measure_theory_66895ba3da05558127228a3c438c5e8a19adce3c.png) .
.
The following statements are equivalent:
 is measurable.
is measurable. we have
we have ![$f^{-1} \big( (c, \infty] \big) \in \mathcal{A}$](../../assets/latex/measure_theory_a1403a63281df14e6f9406be7d355f985890dd71.png) .
. we have
we have ![$f^{-1} \big( [c, \infty] \big) \in \mathcal{A}$](../../assets/latex/measure_theory_7f928ebba157d8b0e32bf8ad73e9fa2873ab57d7.png) .
.![$\forall c \in (- \infty, \infty]$](../../assets/latex/measure_theory_16961a674cf394a5edb55231552df5ef2387dc61.png) we have
we have 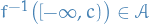 .
. we have
we have ![$f^{-1} \big( [-\infty, c] \big) \in \mathcal{A}$](../../assets/latex/measure_theory_279d8a31d560b94f35569ec9df587984d4a28e58.png) .
.
A function 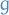 is measurable if
is measurable if
![\begin{equation*}
\forall c \in [- \infty, \infty) : f^{-1} \Big( (c, \infty] \Big) \in \mathcal{A}
\end{equation*}](../../assets/latex/measure_theory_cf13df725bd4ef04ae4396b0f5bcc9e8fdddb4bf.png)
We also observe that by Proposition proposition:equivalent-statements-to-being-a-measurable-function, it's sufficient to prove
![\begin{equation*}
\forall c \in (-\infty, \infty) : f^{-1} \big( [c, \infty] \big) \in \mathcal{A}
\end{equation*}](../../assets/latex/measure_theory_8e5e1bcca38b5b97bece913a91079e5c8dbc7a7d.png)
so that's what we set out to do.
For  and
and  , consider the following equivalent statements:
, consider the following equivalent statements:
![\begin{equation*}
\begin{align*}
& & x &\in \bigg( \inf_{n \ge m} f_n \bigg)^{- 1} \Big( [c, \infty] \Big) \\
& & \inf_{n \ge m} f_n(x) &\in [c, \infty] \\
& & \inf_{n \ge m} f_n(x) &\ge c \\
&\forall n \ge m : & f_n(x) &\ge c \\
& \forall n \ge m : & x & \in f_n^{-1} \big( [c, \infty \big) \\
& & x & \in \bigcap_{n \ge m}^{\infty} f_n^{-1} \big( [c, \infty] \big)
\end{align*}
\end{equation*}](../../assets/latex/measure_theory_94af009dc1af4db3187dfbf9a593271d7e6f84f7.png)
Thus,
![\begin{equation*}
\Big( \inf_{n \ge m} f_n \Big)^{-1} \big( [c, \infty] \big) = \bigcap_{n \ge m}^{} f_n^{-1} \big( [c, \infty] \big)
\end{equation*}](../../assets/latex/measure_theory_50a948d91ff66fee7b9175dd150be89b0439004f.png)
so
![\begin{equation*}
\big( \inf_{n \ge m} f_n \big)^{-1} \big( [c, \infty] \big) \in \mathcal{A}
\end{equation*}](../../assets/latex/measure_theory_e82c9dc08e0706905a550f6f6dcfba1d845ac5bb.png)
Recall that for each  , the sequence
, the sequence  is an increasing sequence in
is an increasing sequence in  . Therefore, similarily, the following are equivalent:
. Therefore, similarily, the following are equivalent:
![\begin{equation*}
\begin{align}
& & x & \in \big( \liminf_{n \to \infty} f_n \big)^{- 1} \big( [c, \infty] \big) \\
& & \liminf_{n \to \infty} f_n(x) & \in [c, \infty] \\
& & \uparrow \lim_{m \to \infty} \inf_{n \ge m} f_n(x) &\ge c \\
& & \sup_m \inf_{n \ge m} f_n(x) &\ge c \\
& \forall N \in \mathbb{Z} : \exist m \in \mathbb{N} & \inf_{n \ge m} f_n(x) &\ge c - \frac{1}{N} \\
& \forall N \in \mathbb{N} : & x &\in \bigcup_{m \in \mathbb{N}}^{} \bigg( \inf_{n \ge m} f_n \bigg)^{-1} \bigg( \bigg[ c - \frac{1}{N}, \infty \bigg] \bigg) \\
& & x & \in \bigcap_{N \in \mathbb{N}}^{} \bigcup_{m \in \mathbb{N}}^{} \bigg( \inf_{n \ge m} f_n \bigg)^{-1} \bigg( \bigg[ c - \frac{1}{N}, \infty \bigg] \bigg)
\end{align}
\end{equation*}](../../assets/latex/measure_theory_caecf37c6ca6765e01f08e6648c9e28ae668ffe0.png)
Thus,
![\begin{equation*}
\big( \liminf f_n \big)^{-1} \big( [c, \infty] \big) = \bigcap_{N \in \mathbb{N}}^{} \bigcup_{m \in \mathbb{N}}^{} \bigg( \inf_{n \ge m} f_n \bigg)^{-1} \bigg( \bigg[ c - \frac{1}{N}, \infty \bigg] \bigg)
\end{equation*}](../../assets/latex/measure_theory_c759a8999f8697bf52bd6d4e35f493d7ca24ec11.png)
Hence,
![\begin{equation*}
\big( \liminf f_n \big)^{-1} \big( [c, \infty] \big) \in \mathcal{A}
\end{equation*}](../../assets/latex/measure_theory_e6028aa99aabfafc829083191d1bf45609989c03.png)
concluding our proof!
Basically says the same as Prop. proposition:limits-of-measurable-functions-are-measurable, but a bit more "concrete".
Let  be a
be a 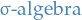 of subsets of a set
of subsets of a set  , and let
, and let  with
with 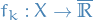 be a sequence of measurable functions.
be a sequence of measurable functions.
Furthermore, let

Then  is a measurable function.
is a measurable function.
Simple functions
Let  be a
be a 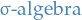 of subsets of a set
of subsets of a set  .
.
A function  is called a simple function if
is called a simple function if
- it is measurable
- only takes a finite number of values
Let  be a
be a 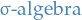 of subsets of a set
of subsets of a set  .
.
Let ![$f : X \to [0, \infty]$](../../assets/latex/measure_theory_79e902dffac5e5c0b65197f8c0b14589c6664f65.png) be a nonnegative measurable function.
be a nonnegative measurable function.
Then there exists a sequence  of simple functions such that
of simple functions such that
 for all
for all 
Converges to
 :
:

Define a function  as follows. Let
as follows. Let
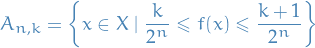
and let

Then the function
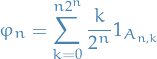
obeys the required properties!
Almost everywhere and almost surely
Let 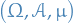 be a measure or probability space.
be a measure or probability space.
Let  be a sequence of measurable functions
be a sequence of measurable functions
- For each
 the function
the function  is measurable
is measurable - The function
 is measurable
is measurable - Thus, if the
 converge pointwise, then
converge pointwise, then  is measurable
is measurable
Let 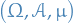 be a measure space. Let
be a measure space. Let  be a condition in oe variable.
be a condition in oe variable.
 holds almost everywhere (a.e.) if
holds almost everywhere (a.e.) if

Let 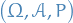 be a probability space and
be a probability space and  be a condition in one variable, then
be a condition in one variable, then  holds almost surely (a.e.) if
holds almost surely (a.e.) if

also denoted
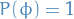
Let 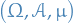 be a complete measure space.
be a complete measure space.
- If
 is measurable and if
is measurable and if  a.e. then
a.e. then 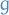 is measurable.
is measurable. - Being equal a.e. is an equivalence relation on measurable functions.
Convergence theorems for nonnegative functions
Problems
Clearly if 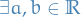 with
with  s.t.
s.t.  , then
, then

hence
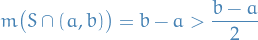
Therefore it's sufficient to prove that if  , then there exists a non-degenerate open interval
, then there exists a non-degenerate open interval 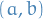 s.t.
s.t.  . (first I said contained in
. (first I said contained in  , but that is a unecessarily strong statement; if contained then what we want would hold, but what we want does not imply containment).
, but that is a unecessarily strong statement; if contained then what we want would hold, but what we want does not imply containment).
As we know, for every  there exists
there exists  such that
such that  and
and

Which implies

which implies
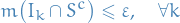
Letting  , this implies that there exists an open cover
, this implies that there exists an open cover  s.t.
s.t.

and

(this fact that this is true can be seen by considering  for all
for all  and see that this would imply
and see that this would imply  not being a cover of
not being a cover of  , and if
, and if 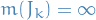 , then since
, then since 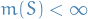 there exists a "smaller" cover).
there exists a "smaller" cover).
Thus,

Hence, letting  be s.t.
be s.t.

we have

as wanted!
 , we have
, we have  for almost every
for almost every  if and only if for almost every
if and only if for almost every  ,
,  for all
for all  .
.
This is equivalent to saying
![\begin{equation*}
m \Big( f_n^{-1} \big( (-\infty, 0] \big) \Big) = 0, \quad \forall n \in \mathbb{N}
\end{equation*}](../../assets/latex/measure_theory_67584d2b69d979eee0f59c423a7e6cfbc7c4b82a.png)
if and only if
![\begin{equation*}
m \bigg( \bigcup_{n = 0}^{\infty} f_n^{-1} \Big( (-\infty, 0] \Big) \bigg) = 0
\end{equation*}](../../assets/latex/measure_theory_4acf342f12fd15b4c6d3b130fe41fb4825810116.png)
i.e.  is a set of measure zero.
is a set of measure zero.
 Then clearly
Then clearly
![\begin{equation*}
m \bigg( \bigcup_{n=0}^{\infty} f_n^{-1} \big( (- \infty, 0] \big) \bigg) = \sum_{n=0}^{\infty} \underbrace{m \Big( f_n^{-1} \big( (- \infty, 0] \big) \Big)}_{= 0} = 0
\end{equation*}](../../assets/latex/measure_theory_b5c3b4a7db26f3d66f1400bc53d458741769e23b.png)
by the assumption.
 Follows by the same logic:
Follows by the same logic:
![\begin{equation*}
\sum_{n=0}^{\infty} m \Big( f_n^{-1} \big( (- \infty, 0] \big) \Big) = \underbrace{m \bigg( \bigcup_{n=0}^{\infty} f_n^{-1} \big( (- \infty, 0] \big) \bigg)}_{= 0} = 0
\end{equation*}](../../assets/latex/measure_theory_6b06dbd7651e8132421b8a66be9d25590a352936.png)
This concludes our proof.
Integration
Notation
We let
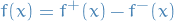
where

Stuff
Let
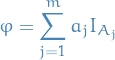
where  are a set of positive values.
are a set of positive values.
Then the integral  of
of  over
over  wrt.
wrt.  is given by
is given by
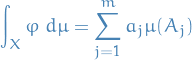
Let  be a sequence of nonnegative measurable functions on
be a sequence of nonnegative measurable functions on  . Assume that
. Assume that
 for each
for each 
 for each
for each  .
.
Then, we write  pointwise.
pointwise.
Then  is measurable, and
is measurable, and

Let  . By Proposition proposition:limit-of-measurable-functions-is-measurable,
. By Proposition proposition:limit-of-measurable-functions-is-measurable,  is measurable.
is measurable.
Since each  satisfies
satisfies  , we know
, we know  .
.
- If
 , then since
, then since  and for all
and for all  we have
we have  , and
, and  .
.
Let 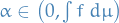 and
and  .
.
Step 1: Approximate  by a simple function.
by a simple function.
Let  be a simple function such that
be a simple function such that  and
and  .
Such an
.
Such an  exists by definition of Lebesgue integral. Thus, there are
exists by definition of Lebesgue integral. Thus, there are  such that
such that  , and disjoint mesurable sets
, and disjoint mesurable sets  such that
such that
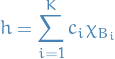
If any  , it doesn't contribute to the integral, so we may ignore it and assume that there are no such sets.
, it doesn't contribute to the integral, so we may ignore it and assume that there are no such sets.
Step 2: Find sets of large measure where the convergence is controlled.
Note that for all  we have
we have

That is, for each  and
and  ,
,

For  and
and  , let
, let
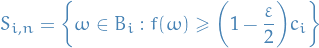
And since it's easier to work with disjoint sets,
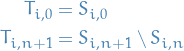
Observe that,

Then,
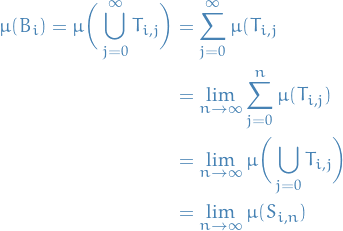
We don't have a "rate of convergence" on 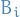 , but on
, but on  we know that we are
we know that we are 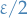 close, and so we can "control" the convergence.
close, and so we can "control" the convergence.
Step 3: Approximate  from below.
from below.
For each  if
if  , then let
, then let  be such that
be such that

and otherwise, let  be such that
be such that
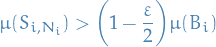
Let 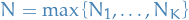 , and let
, and let  .
.
For each  ,
,  and
and  we have
we have
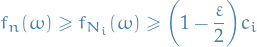
Thus,  , and
, and  ,
,
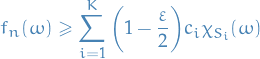
If there is a  such that
such that  , then
, then
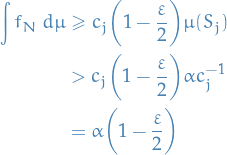
Otherwise (if the integral is finite), then
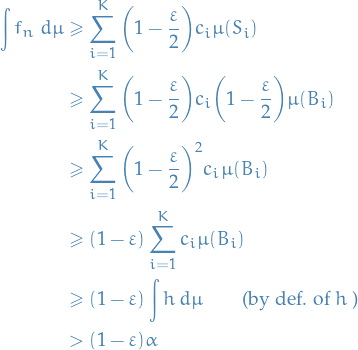
For every 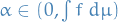 and
and  , there is an
, there is an  such that
such that
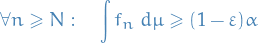
For every 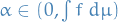 such that
such that
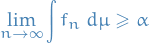
Therefore

Thus,
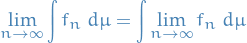
as wanted.
Let  be any nonnegative measurable functions on
be any nonnegative measurable functions on  .
.
Then

Let  and observe
and observe  are pointwise increasing
are pointwise increasing
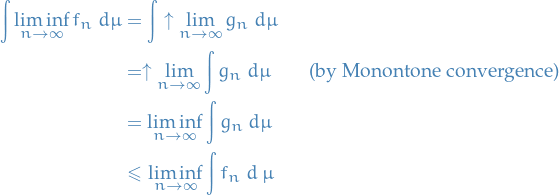
Properties of integrals
Let 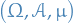 be a measure space.
be a measure space.
If  is a nonnegative measurable function, then there is an increasing sequence of simple functions
is a nonnegative measurable function, then there is an increasing sequence of simple functions  such that
such that
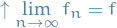
Given  as above and
as above and  for
for  , let
, let
![\begin{equation*}
\begin{split}
S_{n, k} &= f^{-1} \Big( \big[k 2^{-n}, (k + 1) 2^{-n} \big) \Big) \\
S_{n, 4^n} &= f^{-1} \Big( [2^n, \infty] \Big)
\end{split}
\end{equation*}](../../assets/latex/measure_theory_aa6b395505b8bd8701e0668288bf3f46245d7906.png)
and
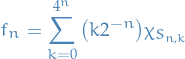
Or a bit more explicit (and maybe a bit clearer),
![\begin{equation*}
f_n = \underbrace{4^n 2^{-n}}_{= 2^n} \chi_{f^{-1} \Big( [2^n, \infty] \Big)} + \sum_{k=0}^{4^n - 1} \big( k 2^{-n} \big) \chi_{f^{-1} \Big( \big[\frac{k}{2^n}, \frac{k + 1}{2^n} \big) \Big)
\end{equation*}](../../assets/latex/measure_theory_bc744558768b4a547f739ded454eaedaafbc4971.png)
For each  ,
,  is a cover of
is a cover of  . On each
. On each  we have
we have  , hence
, hence  on entirety of
on entirety of  .
.
Consider  . If
. If  , then for
, then for 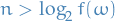 which in turn implies
which in turn implies

Hence  .
.
Finally, if  , then
, then 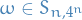 and for all
and for all 
 take on values
take on values

Hence,  for all cases.
for all cases.
Furthermore, for any  and
and  , there is the nesting property
, there is the nesting property

so on  we have
we have  .
.
(This can be seen by observing that what we're really doing here is dividing the values  takes on into a grid, and observing that if we're in
takes on into a grid, and observing that if we're in  then we're either in
then we're either in 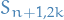 or
or 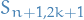 ).
).
For  , then
, then
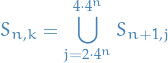
so again  and
and  is pointwise increasing.
is pointwise increasing.
Let 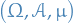 be a measure space.
be a measure space.
Let
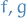 be nonnegative, measurable functions
be nonnegative, measurable functions![$\alpha \in [0, \infty]$](../../assets/latex/measure_theory_37d5fe22c2c90662a9b0b8b33308006a3475d65c.png) s.t.
s.t.

is defined
 be a sequence of nonnegative measurable functions.
be a sequence of nonnegative measurable functions.
Then
Finite sum
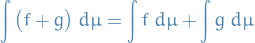
Scalar multiplication
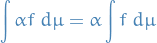
Infinte sums
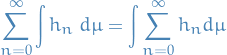
Let  and
and  be increasing sequence of simple functions converging to
be increasing sequence of simple functions converging to  ,
,  , respectively.
, respectively.
Note  is aslo increasing to
is aslo increasing to  .
.
By monotone convergence theorem
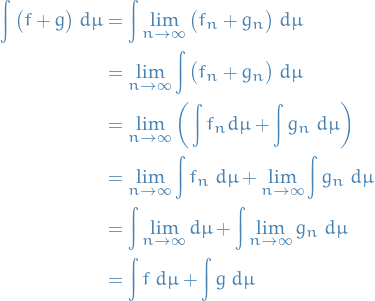
The argument is similar for products.
Finally, 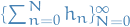 is an increasing sequence of nonnegative measurable functions, since sums of measurable functions is a measurable function.
is an increasing sequence of nonnegative measurable functions, since sums of measurable functions is a measurable function.
Thus, by monotone convergence and the result for finite sums
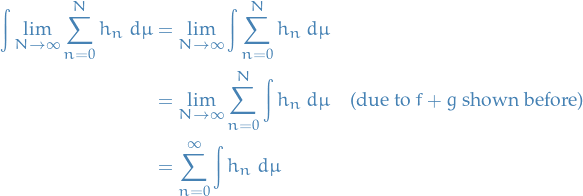
Integrals on sets
Let  be a measure or probability space.
be a measure or probability space.
If  is a sequence of disjoint measurable sets then
is a sequence of disjoint measurable sets then
Let 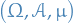 be a measure or probability space.
be a measure or probability space.
If  is a simple function and
is a simple function and  is a measurable set, then
is a measurable set, then 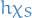 is a simple function.
is a simple function.
Let 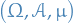 be a measure or probability space.
be a measure or probability space.
Let  be a nonnegative measurable function and
be a nonnegative measurable function and  .
.
The integral of  on
on  is defined to be
is defined to be
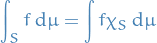
Let 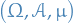 be a measure or probability space.
be a measure or probability space.
Let  be a nonnegative measurable function.
be a nonnegative measurable function.
If
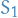 and
and 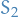 are disjoint measurable sets, then
are disjoint measurable sets, then
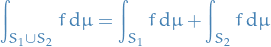
If
 are disjoint measurable sets, then
are disjoint measurable sets, then
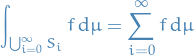
Let 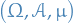 be a measure or probability space.
be a measure or probability space.
If  is a nonnegative measurable function, then
is a nonnegative measurable function, then ![$\mu_f: \mathcal{A} \to [0, \infty]$](../../assets/latex/measure_theory_5431344eb18be9cd48ff98f38d15812bb8f3f3a3.png) defined by
defined by  :
:
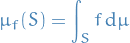
is a measure on  .
.
If  , then
, then ![$P_f: \mathcal{A} \to [0, \infty]$](../../assets/latex/measure_theory_595ab36a9344eed11eb64916b5fa997660643f02.png) defined by
defined by  :
:

The (real) Gaussian measure on  is defined as:
is defined as:
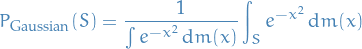
where  denotes the Lebesgue measure.
denotes the Lebesgue measure.
A Gaussian probability measure can also be defined for an arbitrary Banach space  as follows:
as follows:
Then, we say  is a Gaussian probability measure on
is a Gaussian probability measure on  if and only if
if and only if  is a Borel measure, i.e.
is a Borel measure, i.e.

such that  is a real Gaussian probability measure on
is a real Gaussian probability measure on  for every linear functional
for every linear functional  , i.e.
, i.e.  .
.
Here we have used the notation 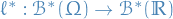 , defined
, defined

where 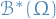 denotes the Borel measures on
denotes the Borel measures on  .
.
Integrals of general functions
Let 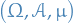 be a measure or probability space.
be a measure or probability space.
If ![$f: \Omega \to [- \infty, \infty]$](../../assets/latex/measure_theory_27db8ee19d1a570b0cf117dd687777fac66160ec.png) is a measurable function, then the positive and negative parts are defined by
is a measurable function, then the positive and negative parts are defined by
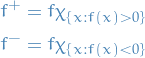
Note:  and
and  are nonnegative.
are nonnegative.
Let 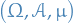 be a measure or probability space.
be a measure or probability space.
If ![$f: \Omega \to [- \infty, \infty]$](../../assets/latex/measure_theory_27db8ee19d1a570b0cf117dd687777fac66160ec.png) is a measurable function, then
is a measurable function, then  and
and  are measurable functions.
are measurable functions.
Let 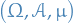 be a measure or probability space.
be a measure or probability space.
- A nonnegative function is defined to be integrable if it is measurable and
 .
. - A function
 is defined to be integrable if it is measurable and
is defined to be integrable if it is measurable and  is integrable.
is integrable.
For an integrable function  , the integral of
, the integral of  is defined to be
is defined to be
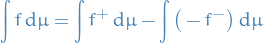
On a set  , the integral is defined to be
, the integral is defined to be
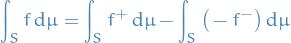
Note that  , but in the actual definition of the integral, we use
, but in the actual definition of the integral, we use  .
.
Let 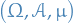 be a measure or probability space.
be a measure or probability space.
If  and
and 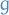 are real-valued integrable functions and
are real-valued integrable functions and  , then
, then
(Scalar multiplication)
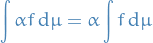
(Additive)
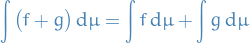
Let 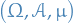 be a measure or probability space.
be a measure or probability space.
Let  and
and 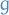 be measurable functions s.t.
be measurable functions s.t.

If 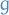 is integrable then
is integrable then  is integrable.
is integrable.
Examples
Consider  with Lebesgue measure. Is
with Lebesgue measure. Is 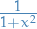 integrable?
integrable?
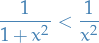
And
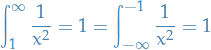
and
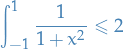
therefore
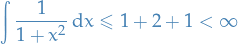
Thus, 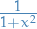 is integrable.
is integrable.
Lebesge dominated convergence theorem
Let 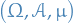 be a measure or probability space.
be a measure or probability space.
Let 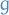 be a nonnegative integrable function and let
be a nonnegative integrable function and let  be a sequence of (not necessarily nonnegative!) measurable functions.
be a sequence of (not necessarily nonnegative!) measurable functions.
Asssume 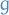 and all
and all  are real-valued.
are real-valued.
If  and
and  such that
such that

and the pointwise limit
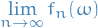
exists.
Then
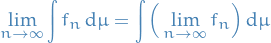
That is, if there exists a "dominating function"  , then we can "move" the limit into the integral.
, then we can "move" the limit into the integral.
Since  and
and  such that
such that  , we find
, we find  that
that 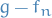 and
and  are nonnegative.
are nonnegative.
Consider 
From Fatou's lemma, we have
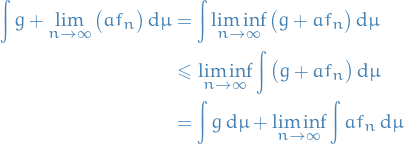
Therefore

Consider 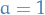 , then
, then

(this looks very much like Fatou's lemma, but it ain't;  does not necessarily have to be nonnegative as in Fatou's lemma)
does not necessarily have to be nonnegative as in Fatou's lemma)
Consider 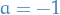
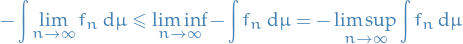
Therefore,

Which implies
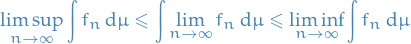
Since  , we then have
, we then have  exists and is equal to
exists and is equal to  .
.
Examples of failure of dominated convergence
Where dominated convergence does not work
On  with Lebesgue measure, consider
with Lebesgue measure, consider
![\begin{equation*}
\begin{split}
f_n &= \chi_{[n, n + \frac{1}{2}]} \\
g_n &= \arctan \big( x - n \big) + \frac{\pi}{2}
\end{split}
\end{equation*}](../../assets/latex/measure_theory_86b9124678b092e327558bdc249245b93ada07c3.png)
such that ![$g_n \in [0, \pi]$](../../assets/latex/measure_theory_1cda4a0be5367504c88a0871f4e46c2cc110f596.png) instead of
instead of ![$[- \frac{\pi}{2}, \frac{\pi}{2}]$](../../assets/latex/measure_theory_4c0845ce4ba68814a80ace45d8f5f56fddfec79f.png) as "usual" with
as "usual" with  .
.
Both of these are nonnegative sequences that converge to  pointwise.
pointwise.
Notice there is no integrable dominating function for either of these sequences:
 would require a dominating function to have infinite integral, therefore no dominating integrable function exists.
would require a dominating function to have infinite integral, therefore no dominating integrable function exists. on the right, and so a dominating function would have to be above
on the right, and so a dominating function would have to be above 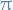 on some interval
on some interval 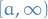 which would lead to infinite integral.
which would lead to infinite integral.
Thus, Lebesgue dominated convergence does not apply
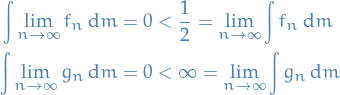
Noncummtative limits: simple case

Noncommutative limits: another one
Consider  with Lebesgue measure and
with Lebesgue measure and
![\begin{equation*}
f(x) = \frac{1}{x} \chi_{[1, \infty)} - \frac{1}{\left| x \right|} \chi_{(-\infty, -1]}
\end{equation*}](../../assets/latex/measure_theory_14635fa0f57a58ce700b3856836b8bcda95d51e0.png)
Consider  and $ b > 1$ and
and $ b > 1$ and
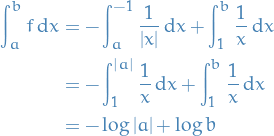
Note that  , so
, so  is not integrable.
is not integrable.
Consider
![\begin{equation*}
\begin{split}
\lim_{N \to \infty} \int \chi_{[-N, N]} f \dd{x} &= \lim_{N \to \infty} \Big( - \log \left| - N \right| + \log N \Big) = \lim_{N \to \infty} 0 = 0 \\
\lim_{N \to \infty} \int \chi_{[-N, 2N]} f \dd{x} &= \lim_{N \to \infty} \Big( - \log N + \log 2N \Big) = \lim_{N \to \infty} \log 2 = \log 2
\end{split}
\end{equation*}](../../assets/latex/measure_theory_7503b43d535ab9bfd060eaa19b94e17bd2de244e.png)
Commutative limits
Consider
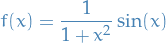
![\begin{equation*}
\lim_{N \to \infty} \lim_{M \to \infty} \int \chi_{[-M, N]} f \dd{x} = \lim_{M \to \infty} \lim_{N \to \infty} \int \chi_{[- M, N]} f \dd{x}
\end{equation*}](../../assets/latex/measure_theory_1591ddcfb29c1faa905731373db01dfdb888bb3e.png)
We know that 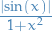 is integrable and for all
is integrable and for all  and
and  ,
,

By multiple applications of LDCT
![\begin{equation*}
\begin{split}
\lim_{N \to \infty} \lim_{M \to \infty \to \infty} \int \chi_{[-M, N]} f \dd{x} &= \lim_{N \to \infty} \int \chi_{(-\infty, N]} f \dd{x} \\
&= \int \chi_{(-\infty, \infty)} f \dd{x} \\
&= \int f \dd{x} \\
&= \int \chi_{(-\infty, \infty)} f \dd{x} \\
&= \lim_{M \to \infty} \int \chi_{[-M, \infty)} f \dd{x} \\
&= \lim_{M \to \infty} \lim_{N \to \infty} \int \chi_{[-M, N]} f \dd{x}
\end{split}
\end{equation*}](../../assets/latex/measure_theory_dbd2a8cecbc43b92c2b5adc3837df5b30a770f80.png)
Showing that in this case the limits do in fact commute.
Riemann integrable functions are measurable
All Riemann integrable functions are measurable.
For any Riemann integrable function, the Riemann integral and the Lebesgue integral are equal.
Almost everywhere and Lp spaces
If  is a nonnegative, measurable function, and
is a nonnegative, measurable function, and  , then
, then  .
.
For  , let
, let
![\begin{equation*}
\begin{split}
T_0 &= f^{-1} \Big( (1, \infty] \Big) \\
T_n &= f^{-1} \bigg( \bigg( \frac{1}{n + 1}, \frac{1}{n} \bigg] \bigg), \quad n \in \mathbb{Z}^+
\end{split}
\end{equation*}](../../assets/latex/measure_theory_2ceab74592bc736a2823d5c8f0aa92dafd661f57.png)
Observe the  are disjoint and
are disjoint and
![\begin{equation*}
\bigcup_{i = 1}^{\infty} T_i = f^{-1} \bigg( (0, \infty] \bigg)
\end{equation*}](../../assets/latex/measure_theory_93b55f6349b02c3782503473a25b3f7b47350719.png)
Suppose that  . This implies that
. This implies that  on a set of positive measure, i.e.
on a set of positive measure, i.e.
![\begin{equation*}
\mu \bigg( f^{-1} \Big( (0, \infty] \Big) \bigg) > 0
\end{equation*}](../../assets/latex/measure_theory_e85507015506242700deeda1834343a94f438944.png)
but this implies that
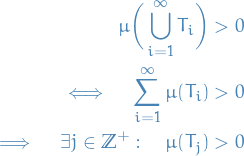
Thus,
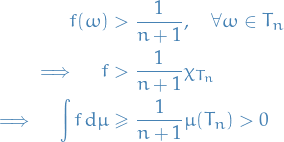
which is a contradiction, hence  .
.
Let  and
and 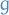 be integrable.
be integrable.
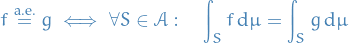
 is the set of all equivalence classes of integrable functions wrt. the equivalence relation given by a.e. equality, i.e.
is the set of all equivalence classes of integrable functions wrt. the equivalence relation given by a.e. equality, i.e.

If  is an integrable function, the
is an integrable function, the  norm is
norm is
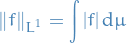
If ![$[f] \in L^1(\dd{\mu})$](../../assets/latex/measure_theory_febf1d9c9d9fc46e4fc2d9e79dd425642660a25e.png) and
and ![$g \in [f]$](../../assets/latex/measure_theory_0674799b02ef974d9bce66406bc2481c9c7bb951.png) , the integral and norm are defined to be
, the integral and norm are defined to be
![\begin{equation*}
\begin{split}
\int [f] \dd{\mu} &= \int g \dd{\mu} \\
\norm{[f]}_{L^1} &= \norm{g}_{L^1}
\end{split}
\end{equation*}](../../assets/latex/measure_theory_6917d223cd066748131b36bb5557b619ee598345.png)
If ![$[f], [g], [h] \in L^1$](../../assets/latex/measure_theory_e32b14a7500cc43f20c1a1657905bfee0ed6d43e.png) , then
, then ![$[f + g] \in L^1$](../../assets/latex/measure_theory_9ee9da136403a0f769d8056adb9124c5934f6f3f.png) , and
, and
![\begin{equation*}
\norm{[f - g]}_{L^1} \le \norm{f - g}_{L^1} + \norm{[h - g]}_{L^1}
\end{equation*}](../../assets/latex/measure_theory_280aa5fd4f0f61951e29cf2fba4c67eb4af32159.png)
 is a real vector space with addition and scalar multiplication given pointwise almost everywhere.
is a real vector space with addition and scalar multiplication given pointwise almost everywhere.
Functions taking on  on a set of zero measure are fine!
on a set of zero measure are fine!
These functions are still the almost everywhere equal to some integrable function (even those these infinite-valued functions are integrable), hence these are in  .
.
Let ![$\left\{ [f_k] \right\}$](../../assets/latex/measure_theory_adf0c6a74e755c8ef23b722bb511497982e81a93.png) be a Cauchy sequence. Since the
be a Cauchy sequence. Since the  are integrable, we may assume we choose
are integrable, we may assume we choose  valued representatives.
valued representatives.
For  , let
, let  be such that for
be such that for  ,
,

and 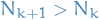 .
.
Thus,
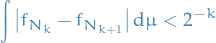
and
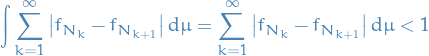
Thus,  is finite almost everywhere. Thus, this series is infinite on a set of measure zero, so we may assume the representatives
is finite almost everywhere. Thus, this series is infinite on a set of measure zero, so we may assume the representatives  are zero there and the sum is finite at each
are zero there and the sum is finite at each  .
.
Thus,  converges everywhere.
converges everywhere.
Let
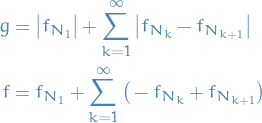
(observe that the last part is just rewriting the 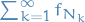 ).
).
By monotone convergence theorem
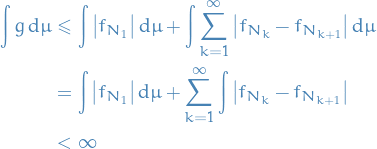
Observe that pointwise
Applications to Probability
Notation
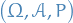 is a probability space
is a probability space- Random variable
 is a measurable function
is a measurable function 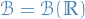 denotes the Borel sigma-algebra on
denotes the Borel sigma-algebra on 
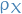 denotes the probability distribution measure for
denotes the probability distribution measure for 
 be a sequence of random events
be a sequence of random events be a sequence of finitely many random events
be a sequence of finitely many random events
Probability and cumulative distributions
An elementary event is an element of  .
.
A random event is an element of 
A random variable is a measurable function from 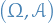 to
to ![$\Big( [- \infty, \infty], \mathcal{B} \big( [- \infty, \infty] \big) \Big)$](../../assets/latex/measure_theory_71661c6fca4577bd7a8dc72d729db6c0c7455aef.png) .
.
Let
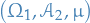 be a measure space and
be a measure space and 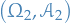 be a measurable space
be a measurable space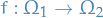 be a measurable function
be a measurable function
Then we say that the push-forward of  by
by  is defined
is defined

The probability distribution measure of  , denoted
, denoted ![$\rho_X: \mathcal{B}(\mathbb{R}) \to [0, 1]$](../../assets/latex/measure_theory_a5c7220fd4e2a7451ed9120399b51f8339ac82f6.png) , is defined
, is defined
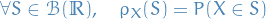
Equivalently, it's the push-forward of  by
by  :
:

In certain circles not including measure-theorists (existence of such circles is trivial), you might hear talks about "probability distributions". Usually what is meant by this is 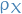 for some random variable
for some random variable  .
.
That is, a "distribution of  " usually means that there is some probability space
" usually means that there is some probability space  in which
in which  is a random variable, i.e.
is a random variable, i.e.  and the "distribution of
and the "distribution of  " is the corresponding probability distribution measure!
" is the corresponding probability distribution measure!
Confusingly enough, they will often talk about " distribution of
distribution of  ", in which case
", in which case  is NOT a probability measure, but denotes a probability distribution measure of the random variable.
is NOT a probability measure, but denotes a probability distribution measure of the random variable.
The cumulative distribution function of  , denoted
, denoted ![$F_X: \mathbb{R} \to [0, 1]$](../../assets/latex/measure_theory_857de4732cc5895e72b48743bb1ed0b6c6ef9120.png) , is defined by
, is defined by
![\begin{equation*}
\forall x \in \mathbb{R}, \quad F_X(x) = P(X \le x) = \rho_X \big( (- \infty, x] \big)
\end{equation*}](../../assets/latex/measure_theory_1135df16d8d98e78eda428fdded8af11029fc26f.png)
where 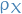 is the probability distribution measure of
is the probability distribution measure of  .
.
The probability distribution measure 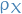 is a probability measure on the Borel sets
is a probability measure on the Borel sets  .
.

If  is a disjoint sequence of sets in
is a disjoint sequence of sets in  , then
, then
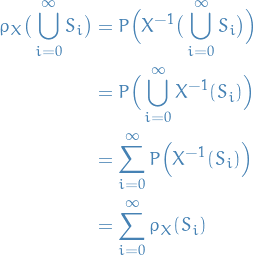
so 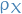 satisfies countable additivity and is a measure.
satisfies countable additivity and is a measure.
Finally,

so 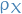 is a probability measure.
is a probability measure.
 is increasing
is increasing and
and 
 is right continuous (i.e. continuous from the right)
is right continuous (i.e. continuous from the right)
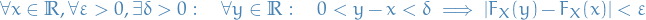
If
 , then
, then
![\begin{equation*}
\begin{split}
F_X(x) &= P(X \le x) \\
&= P \Big( X^{-1} \big( (- \infty, x] \big) \Big) \\
& \le P \Big( X^{-1} \big( ( -\infty, x] \big) \Big) + P \Big( X^{-1} \big( (x, y] \big) \Big) \\
&= P \Big( X^{-1} \big( (-\infty, x] \cup (x, y] \big) \Big) \\
&= P \Big( X^{-1} \big( (- \infty, y] \big) \Big) \\
&= F_X(y)
\end{split}
\end{equation*}](../../assets/latex/measure_theory_02e5898fb6b34b5dbd3e516b4c58fb5d27ddfe1b.png)
Consider the limit as
 . Let
. Let
![\begin{equation*}
\begin{split}
T_0 &= X^{-1} \big( (- \infty, 0] \big) \\
T_n &= X^{-1} \big( (n - 1, n] \big), \quad \forall n \in \mathbb{Z}^+
\end{split}
\end{equation*}](../../assets/latex/measure_theory_822502b5a0806137387a045422e41a8d00ed4b6e.png)
so
Then,
![\begin{equation*}
\begin{split}
1 &= P (\Omega) = P \bigg( \bigcup_{i=0}^{\infty} T_i \bigg) \\
&= \lim_{n \to infty} \sum_{i=0}^{n} P(S_i) \\
&= \lim_{n \to \infty} \bigg( P \Big( X^{-1} \big( (- \infty, 0] \big) \Big) \bigg) + \sum_{i=1}^{n} P \bigg( X^{-1} \Big( (n - 1, n] \Big) \bigg) \\
&= \lim_{n \to \infty} P \bigg( X^{-1} \Big( (- \infty, n] \Big) \bigg) \\
&= \lim_{n \to \infty} F_X(n)
\end{split}
\end{equation*}](../../assets/latex/measure_theory_c85daac3994fefdf28c3cd1e69dd2a502d02db52.png)
which, since
 is increasing implies
is increasing implies

Let
 and
and  . Let
. Let
![\begin{equation*}
S_n = \bigg( x, x + \frac{1}{n} \bigg]
\end{equation*}](../../assets/latex/measure_theory_71877cd7b7156217e1f928f060006ff74416c33a.png)
The
 are nested, and similarily
are nested, and similarily 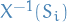 are nested.
are nested.
![\begin{equation*}
\begin{split}
0 &= P (\emptyset) = P \bigg( x^{-1} \bigg( \bigcup_{i=0}^{\infty} S_i \bigg) \bigg) \\
&= \lim_{n \to \infty} P \Big( X^{-1}(S_n) \Big) \\
&= \lim_{n \to \infty} P \bigg( X^{-1} \bigg( \bigg(x, x + \frac{1}{n} \bigg] \bigg) \bigg) \\
&= \lim_{n \to \infty} P \bigg( X^{-1} \bigg( \bigg( - \infty, x + \frac{1}{n} \bigg] \bigg) \bigg) - P \bigg( X^{-1} \bigg( \bigg(-\infty, x \bigg] \bigg) \bigg) \\
&= \lim_{n \to \infty} \bigg[ F_X \bigg( x + \frac{1}{n} \bigg) - F_X(x) \bigg]
\end{split}
\end{equation*}](../../assets/latex/measure_theory_3f72b108040e545c8a2dbe673817e5955c4dd7a7.png)
Thus, given
 , there exists
, there exists  such that
such that

Let
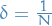 so
so

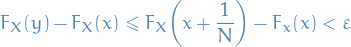
Radon-Nikodym derivatives and expectations
Let
 be a rv.
be a rv. its probability distribution measure
its probability distribution measure its cumulative distribution function
its cumulative distribution function a Borel measureable function
a Borel measureable function
The following are equivalent:
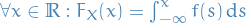
 is a Radon-Nikodym derivative for
is a Radon-Nikodym derivative for 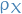 wrt.
wrt.  (the Lebesgue measure but restricted to Borel measurable sets)
(the Lebesgue measure but restricted to Borel measurable sets)
(2) and (3) are immediately equivalent:
![\begin{equation*}
\rho_X \Big( (- \infty, x] \Big) = F_X(x) = \int_{-\infty}^{x} f(s) \dd{s} = \int_{-\infty}^{x} f \dd{m}
\end{equation*}](../../assets/latex/measure_theory_6826f1b8d841609a361882c3b6b70bc5ea1174ef.png)
iff (2) or (3) holds when considering only sets of the form ![$(- \infty, x]$](../../assets/latex/measure_theory_e122470acfe9dda86dc876d6b068fadc47cc17be.png) .
.
This statement is also equivalent to (1).
Thus (1) is equivalent to (2) or (3) restricted to sets of the form ![$(-\infty, x]$](../../assets/latex/measure_theory_4da7df6ea37290e01a6b13bd339c125dc9d812cd.png) .
.
However, sets of the form ![$(-\infty, x]$](../../assets/latex/measure_theory_4da7df6ea37290e01a6b13bd339c125dc9d812cd.png) generate
generate  , so from the Carathéodory extension theorem this gives
, so from the Carathéodory extension theorem this gives  .
.
To prove  more rigorously, let
more rigorously, let

for ![$c_i, d_i \in [-\infty, \infty]$](../../assets/latex/measure_theory_879949f8d7167858f9f8cf9fe0fb70cc850702cf.png) s.t.
s.t.  and none of these intervals overlap. That is all finite unions of left-closed, right-open, disjoint intervals.
and none of these intervals overlap. That is all finite unions of left-closed, right-open, disjoint intervals.
Also let
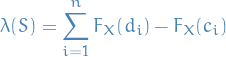
Observe that
![\begin{equation*}
\lambda(S) = \sum_{i=1}^{n} \bigg[ \int_{-\infty}^{d_i} f(x) \dd{x} - \int_{-\infty}^{c_i} f(x) \dd{x} \bigg] = \sum_{i=1}^{n} \int_{c_i}^{d_i} f(x) \dd{x} = \int_S f \dd{m}
\end{equation*}](../../assets/latex/measure_theory_a1afc8f6f2c8e420ab88be7447f2e38b913fb942.png)
and that
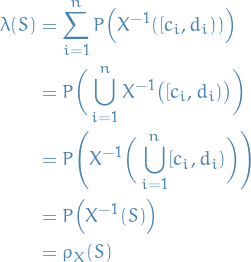
One can show that  is a premeasure space. Therefore, by the Carathéodory extension theorem, there is a measure
is a premeasure space. Therefore, by the Carathéodory extension theorem, there is a measure  on
on  s.t.
s.t.

Furthermore, since 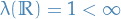 ,
,  is unique! But both the measures
is unique! But both the measures  and
and 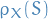 satisfy these properties, thus
satisfy these properties, thus

which is the definition of  being a Radon-Nikodym derivative of
being a Radon-Nikodym derivative of 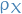 wrt. Lebesgue measure restricted to the Borel σ-algebra, as wanted.
wrt. Lebesgue measure restricted to the Borel σ-algebra, as wanted.
A function  is a probability density function for
is a probability density function for  if
if  is a Radon-Nikodym derivative of the probability distribution measure
is a Radon-Nikodym derivative of the probability distribution measure 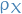 , wrt. Lebesgue measure restricted to Borel sets, i.e.
, wrt. Lebesgue measure restricted to Borel sets, i.e.

Expectation via distributions
Expectation of a random variable is
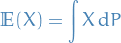
If  is a nonnegative function that is
is a nonnegative function that is  measurable, then
measurable, then
![\begin{equation*}
\mathbb{E} \big[ g(X) \big] = \int g(s) \dd{\rho_X(s)}
\end{equation*}](../../assets/latex/measure_theory_58b872956e73f042002d8b23eb8c33aa0d3cde55.png)
If 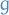 is the characterstic function, then, if
is the characterstic function, then, if 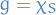 ,
,
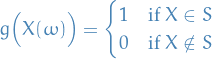
so

Multiplying by constants and summing over different characteristic functions, we get the result to be true for any simple function.
Given a nonnegative function 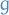 , let
, let  be an increasing sequence of simple functions converging pointwise to
be an increasing sequence of simple functions converging pointwise to  .
.
Note  is the increasing limit of
is the increasing limit of  . By two applications of Monotone Convergence
. By two applications of Monotone Convergence
![\begin{equation*}
\begin{split}
\mathbb{E} \big[ g(X) \big] &= \int g(X) \dd{P}\\
&= \int \lim_{n \to \infty} g_n(X) \dd{P} \quad\\
&= \lim_{n \to \infty} \int g_n(X) \dd{P} \quad \text{(by MC)} \\
&= \lim_{n \to \infty} \int g_n \dd{\rho_X} \quad \text{(by above)}\\
&= \int g \dd{\rho_X} \quad \text{(by MC)}
\end{split}
\end{equation*}](../../assets/latex/measure_theory_011ad9343b3c73146cd5357e27623d0048277ef0.png)
This techinque, of going from characterstic function → simple functions → general functions, is used heavily, not just in probability theory.
Independent events & Borel-Cantelli theorem
A collection of random events  are independent events if for every finite collection of distinct indices
are independent events if for every finite collection of distinct indices  ,
,
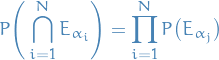
A random event  occurs at
occurs at  if
if  .
.
The probability that the event occurs is  .
.
If  are independent then
are independent then  are also independent.
are also independent.
Prove that  are independent.
are independent.
Consider  , we want to prove
, we want to prove
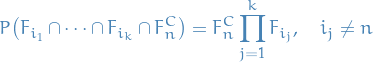
RHS can be written
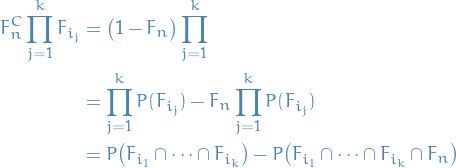
which is equal to LHS above, and implies that the complement is indeed independent.
The condition that infinitively many of the events occurs at  is
is
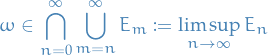
This is equivalent to

where we have converted the  and
and  .
.
Furthermore,  is itself a random event.
is itself a random event.
If
 then probability of infinitely many of the events occuring is 0, i.e.
then probability of infinitely many of the events occuring is 0, i.e.

If the
 are independent and
are independent and  , then probability of infinitely many of the events occuring is 1, i.e.
, then probability of infinitely many of the events occuring is 1, i.e.

Suppose
 .
.
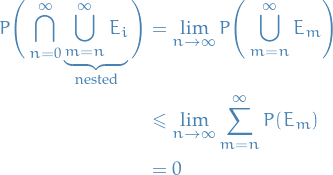
Suppose
 are now independent and that
are now independent and that  .
Fix
.
Fix  . Then
. Then
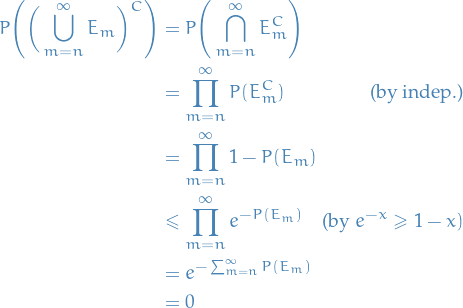
Chebyshev's inequality
Let 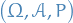 be a probability space.
be a probability space.
If  is a random variable with mean
is a random variable with mean  and variance
and variance 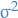 , then
, then

Let
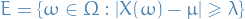
Then 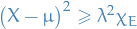 everywhere, so
everywhere, so
![\begin{equation*}
\sigma^2 = \mathbb{E} \big[ \big( X - \mu \big)^2 \big] \ge \lambda^2 \mathbb{E} \big[ \chi_E \big] = \lambda^2 P(E)
\end{equation*}](../../assets/latex/measure_theory_afe5a26fe68a2dc369c6842791542f5d9f5bcae3.png)
Hence,

Independent random variables
Let
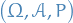 be a probability space.
be a probability space.
A collection of σ-algebras  , where
, where  for all
for all  , is independent if for every collection of events
, is independent if for every collection of events  s.t
s.t  for all
for all  , then
, then  is a set of independent events.
is a set of independent events.
A collection of random variables  is independent if the collection of σ-algebras they generate is independent.
is independent if the collection of σ-algebras they generate is independent.
A sequence of random variables  is independent and identically distributed (i.i.d) if they are independent variables and for
is independent and identically distributed (i.i.d) if they are independent variables and for  we have
we have
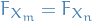
where  is the cumulative distribution function for
is the cumulative distribution function for 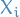 .
.
Let  and
and  be independent.
be independent.
- We have
- If
![$\mathbb{E} \big[ \left| X \right| \big] = 0$](../../assets/latex/measure_theory_f4839615bca9740a070cd50282abcd49b624299c.png) or
or ![$\mathbb{E} \big[ \left| Y \right| \big] = 0$](../../assets/latex/measure_theory_9c2a3e0176324c0303d6e99d95778d8ad8444e90.png) then
then ![$\mathbb{E} \big[ \left| XY \right| \big] = 0$](../../assets/latex/measure_theory_761e7445761b7eb7decf7480a3f579dde5590770.png)
If
![$\mathbb{E} \big[ \left| X \right| \big] > 0$](../../assets/latex/measure_theory_cbb7cd0c3b3a0b7ec2194b26ea2f9c64511309c2.png) and
and ![$\mathbb{E} \big[ \left| Y \right| \big] > 0$](../../assets/latex/measure_theory_d49dbff5ad4b491ca50fc08dbce0112bd500a9ae.png) , then
, then
![\begin{equation*}
\mathbb{E} \big[ \left| XY \right| \big] = \mathbb{E} \big[ \left| X \right| \big] \mathbb{E} \big[ \left| Y \right| \big]
\end{equation*}](../../assets/latex/measure_theory_8da658297f17540bbbc9cb6726bb1d2bbebbc692.png)
- If
Furthermore, if
![$\mathbb{E} \big[ \left| X \right| \big] < \infty$](../../assets/latex/measure_theory_a7ed308ceeb09933497e2a2acc8b07d915339ef8.png) and
and ![$\mathbb{E} \big[ \left| Y \right| \big] < \infty$](../../assets/latex/measure_theory_10ed410a5b735e421f331da4aa674c32c022cda7.png) , then
, then
![\begin{equation*}
\mathbb{E} \big[ XY \big] = \mathbb{E} \big[ X \big] \mathbb{E} \big[ Y \big]
\end{equation*}](../../assets/latex/measure_theory_127c9fbe3926cc0ee673512d405f56dccef62e67.png)
Consider
- first nonnegative functions
- subcase
![$\mathbb{E} \big[ X \big] = 0$](../../assets/latex/measure_theory_384ab7ec94ace068cc33f7a3b4036e557945d4e1.png)
Since  is nonnegative
is nonnegative
![\begin{equation*}
0 = \mathbb{E} \big[ X \big] = \int X \dd{P} \implies X \overset{\text{a.s.}}{=} 0
\end{equation*}](../../assets/latex/measure_theory_3adfb341d10c51cb63db312ac51f907340ca7087.png)
Thus,  so
so ![$\mathbb{E} \big[ XY \big] = 0$](../../assets/latex/measure_theory_ef0626a72b6e48ffbef4e690927fe3ebe3289d4d.png) .
.
Now consider the subcase where ![$\mathbb{E} \big[ X \big] > 0$](../../assets/latex/measure_theory_10c6cdf7c0ab3ad30df17078595f922f9f87633c.png) and
and ![$\mathbb{E} \big[ Y \big] > 0$](../../assets/latex/measure_theory_c59194d819989aa539ba17b5ee03462e949ce8fe.png) .
.
Let 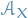 and
and 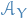 be the σ-algebras generated by
be the σ-algebras generated by  and
and  .
.
Observe that  and
and  are measure spaces. Let
are measure spaces. Let  be an increasing sequence of simple functions that are measurable wrt.
be an increasing sequence of simple functions that are measurable wrt. 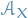 and similarily
and similarily  simple increasing to
simple increasing to  and
and 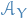 measurable.
measurable.
As simple functions, these can be written as
Then,
![\begin{equation*}
\begin{split}
\mathbb{E} \big[ X_n Y_n \big] &= \int \sum_{i=1}^{M_n} \sum_{j=1}^{N_n} c_{n, i} d_{n, j} \chi_{S_{n, i}} \chi_{T_{n, j}} \dd{P} \\
&= \sum_{i=1}^{M_n} \sum_{j=1}^{N_n} c_{n, i} d_{n, j} P \Big( S_{n, i} \cap T_{n, j} \Big) \\
&= \sum_{i=1}^{M_n} \sum_{j=1}^{N_n} c_{n, i} d_{n, j} P \big( S_{n, i} \big) P \big( T_{n, j} \big) \\
&= \bigg( \sum_{i=1}^{M_n} c_{n, i} P \big( S_{n, i} \big) \bigg) \bigg( \sum_{j=1}^{N_n} d_{n, j} P\big(T_{n, j} \big) \bigg) \\
&= \mathbb{E} \big[ X_n \big] \mathbb{E} \big[ Y_n \big]
\end{split}
\end{equation*}](../../assets/latex/measure_theory_a8103249f0b23d4dc0542716a5f5c9d173d60a25.png)
Since  increases to
increases to  , by MCT
, by MCT
![\begin{equation*}
\mathbb{E} \big[ XY \big] = \mathbb{E} \big[ X \big] \mathbb{E} \big[ Y \big]
\end{equation*}](../../assets/latex/measure_theory_127c9fbe3926cc0ee673512d405f56dccef62e67.png)
Dividing into positive & negative parts & summing gives  .
.
Strong Law of Large numbers
Notation
 are i.i.d. random variables, and we will assume
are i.i.d. random variables, and we will assume
![\begin{equation*}
\mathbb{E}[X_i] < \infty \quad \text{and} \quad \text{Var}(X_i) < \infty
\end{equation*}](../../assets/latex/measure_theory_ce80998071f168839f18af296b335d9ed4193f3a.png)
Stuff
Let 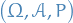 be a probability space and
be a probability space and  be a sequence of i.i.d. random variables with
be a sequence of i.i.d. random variables with
![\begin{equation*}
\mu := \mathbb{E}[X_i] < \infty \quad \text{and} \quad \sigma^2 := \text{Var}(X_i) < \infty
\end{equation*}](../../assets/latex/measure_theory_b5a2be16754e0eac4426741ec560e711c0165643.png)
Then the sequence of random variables 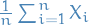 converges almost surely to
converges almost surely to  , i.e.
, i.e.
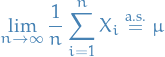
This is equivalent to  occuring with probability 0, and this is the approach we will take.
occuring with probability 0, and this is the approach we will take.
First consider  .
.
For  and
and  , let
, let
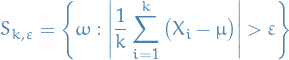
and
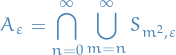
Since  are i.i.d. we have
are i.i.d. we have
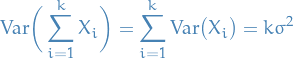
and since variance rescales quadratically,
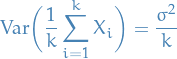
Using Chebyshev's inequality
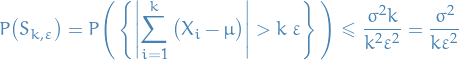
Observe then that with  , we have
, we have
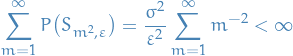
And so by Borel-Cantelli, since this is a sequence of independent random variables, we have

In particular, for any  , there are almost surely only finitely many
, there are almost surely only finitely many  with
with
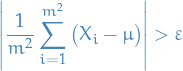
Step: showing that we can do this for any  .
.
Consider  . Observe that by countable subadditivity,
. Observe that by countable subadditivity,

Now let  , which occurs almost surely from the above. For any
, which occurs almost surely from the above. For any  , let
, let

Since  , there are only finitely many
, there are only finitely many  s.t.
s.t.
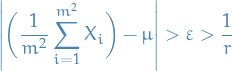
as found earlier (the parenthesis are indeed different here, compared to before). Therefore
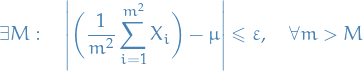
 is arbitrary, so this is true for all
is arbitrary, so this is true for all  . Hence,
. Hence,
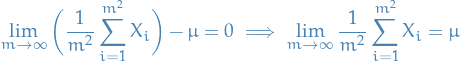
This proves that there is a subsequential limit almost surely.
Step: subsequential limit to "sequential" limit.
Given  , let
, let  be such that
be such that  . Since
. Since 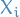 are nonnegative
are nonnegative
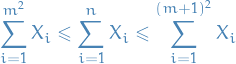
and therefore
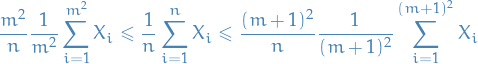
and since  ,
,
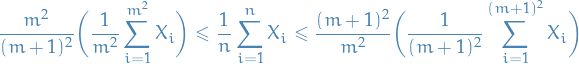
Since the first and the last expressions converge to  ,t by the squeeze theorem we have
,t by the squeeze theorem we have
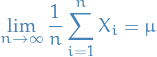
Step: Relaxing nonnegativity assumption on  .
.
Suppose  is not necessarily nonnegative. Since, by assumption,
is not necessarily nonnegative. Since, by assumption,  has finite expectation,
has finite expectation,  is integrable. Therefore we know that the positive and negative parts of
is integrable. Therefore we know that the positive and negative parts of 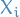 , denoted
, denoted  , are also integrable. Therefore we can compute the expectations
, are also integrable. Therefore we can compute the expectations

Similarily, we have that the variance of  is finite, which allows us to the apply the result we found for
is finite, which allows us to the apply the result we found for  being nonnegative to both
being nonnegative to both  and
and 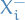 :
:
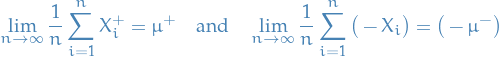
Let  be the set where the mean of the positive / negative part converges. Since
be the set where the mean of the positive / negative part converges. Since
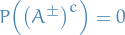
(since otherwise the limit would not converge almost surely). We then have
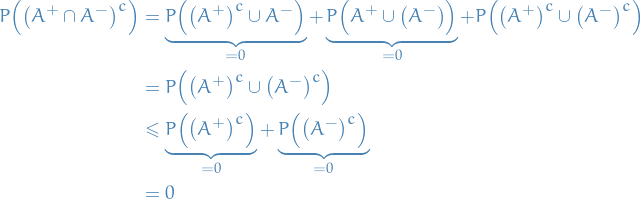
Thus, almost surely,  , and on this we have convergence, so
, and on this we have convergence, so
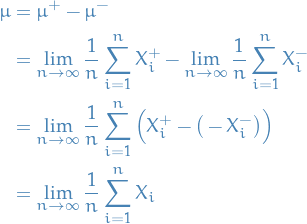
Concluding our proof.
Ergodic Theory
Let  be a measure-preserving transformation on a measure space
be a measure-preserving transformation on a measure space  with
with 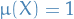 , i.e. it's a probability space.
, i.e. it's a probability space.
Then  is ergodic if for every
is ergodic if for every  we have
we have

Bochner integrable
The Bochner integral is a notion of integrability on Banach spaces, and is defined in very much the same way as integrability wrt. Lebesgue-measure.
Let  be a measure space and
be a measure space and 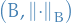 a Banach space.
a Banach space.
A simple function is defined similarily as before, but now taking values on a Banach space instead. That is,
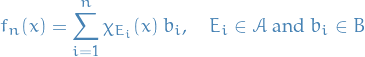
with the integral
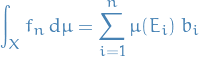
A measurable function  is said to be Bochner integrable if there exists a sequence of integrable simple functions
is said to be Bochner integrable if there exists a sequence of integrable simple functions  such that
such that
where the integral on the LHS is an ordinary Lebesgue integral.
If this is the case, then the Bochner integral is defined
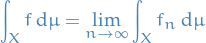
It can indeed be shown that a function  is Bochner integrable if and only if
is Bochner integrable if and only if  , the
, the  Bochner space, defined similarily as L1-space for functions but with the absolute value replaced by the
Bochner space, defined similarily as L1-space for functions but with the absolute value replaced by the  .
.
Concentration inequalities
Stochastic processes
Let
 be a filtration
be a filtration be an
be an  martingale
martingale be an
be an  stopping time
stopping time
such that one of the following holds:
 such that
such that 
![$\mathbb{E}[\tau] < \infty$](../../assets/latex/measure_theory_8df09c95f86cc43dc18e05643b092bcf5c0ed750.png) and there exists a constatn
and there exists a constatn 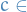 s.t. for all
s.t. for all  ,
,
![\begin{equation*}
\mathbb{E} \big[ \left| X_{t + 1} - X_t \right| \mid \mathcal{F}_t \big] \le c
\end{equation*}](../../assets/latex/measure_theory_f5e02bae54ba58678204010c90aae14d2be4ffb5.png)
almost surely on the even that
 .
.
 such that
such that  almost surely for all
almost surely for all 
Then  is a.s. well-defined and
is a.s. well-defined and ![$\mathbb{E}[X_{\tau}] = \mathbb{E}[X_0]$](../../assets/latex/measure_theory_82948a934352eea2952f8bfe47753bc0c9a3f810.png) .
.
Furthermore, when  is supersub-martingale rather than a martingale, then equality is replaced with lessgreather-than, respectively.
is supersub-martingale rather than a martingale, then equality is replaced with lessgreather-than, respectively.
Let  be a supermartingale with
be a supermartingale with  a.s. for all
a.s. for all  .
.
Then for any 
![\begin{equation*}
\mathbb{P} \bigg( \sup_{t \in \mathbb{N}} X_t \ge \varepsilon \bigg) \le \frac{\mathbb{E}[X_0]}{\varepsilon}
\end{equation*}](../../assets/latex/measure_theory_84492b275ebda66c6570d1bd84ca669f463b7733.png)
Let  be the event that
be the event that  and
and  , where we assume
, where we assume  so that
so that  if
if  for all
for all  .
.
Clearly  is a stopping time and
is a stopping time and  . Then by Doob's optional stopping theorem and an elementary calculation
. Then by Doob's optional stopping theorem and an elementary calculation
![\begin{equation*}
\begin{split}
\mathbb{E} [X_0] & \ge \mathbb{E}[X_{\tau}] \\
&\ge \mathbb{E} \big[ X_{\tau} \1 \left\{ \tau \le n \right\} \big] \\
&\ge \mathbb{E} \big[ \varepsilon \1 \left\{ \tau \le n \right\} \big] \\
&= \varepsilon \mathbb{P} (\tau \le n) = \varepsilon \mathbb{P} (A_n)
\end{split}
\end{equation*}](../../assets/latex/measure_theory_94b8b81bf7fe44c285cfefc52fe78eb1118bd0f2.png)
Course: Advanced Probability
Notation
 is used as a binary operation which takes minimum of the two arguments
is used as a binary operation which takes minimum of the two arguments is used as a binary operation which takes maxmium of the two arguments
is used as a binary operation which takes maxmium of the two arguments
Lecture 1
Notation
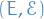 denotes a measurable space (with a measure
denotes a measurable space (with a measure  it becomes a measure space)
it becomes a measure space) denotes the set of measurable functions wrt.
denotes the set of measurable functions wrt. 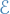

and non-negative measurable functions
![\begin{equation*}
m \mathcal{E}^{ + } := \left\{ f: E \to [0, \infty], f \text{ measurable wrt. } \mathcal{B}(\mathbb{R}) \right\}
\end{equation*}](../../assets/latex/measure_theory_e754d49931a63df28e637dfcfb5d3a5e0caebcb5.png)
We write

Stuff
Let  be a measure space.
be a measure space.
Then there exists a unique ![$\tilde{\mu}: m \mathcal{E}^{ + } \to [0, \infty]$](../../assets/latex/measure_theory_b2e4fdbc02f89d88c2fc919c414c6e74699f8a39.png) s.t.
s.t.
 for all
for all 
Linearity
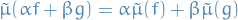
for all
 with
with  .
.
-

for
 pointwise.
pointwise.
There exists a unique measure  on
on  called the product measure
called the product measure
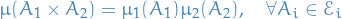
Let  . For
. For  define
define
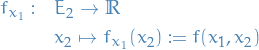
Then  is
is 
 . Hence, we can define
. Hence, we can define
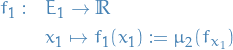
Then  is
is  and
and

where  is the product measure.
is the product measure.
Applying the above in both directions, we have

with
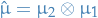
and
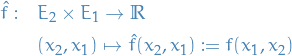
Conclusion:
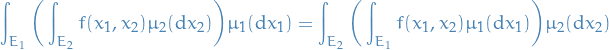
Lecture 2: conditional expectation
Notation
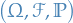 a probability space, i.e.
a probability space, i.e. 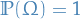
 denotes rv, i.e.
denotes rv, i.e.  is
is  and integrable, with expectation
and integrable, with expectation
![\begin{equation*}
\mathbb{E} \big[ X \big] = \int X \dd{\mathbb{P}}
\end{equation*}](../../assets/latex/measure_theory_fb7b4bd20f047add86c081e6fac8f3cccaf18f89.png)
Also write
![\begin{equation*}
\mathbb{E} \big[ X 1_A \big] = \int_A X \dd{\mathbb{P}}, \quad \forall A \in \mathcal{F}
\end{equation*}](../../assets/latex/measure_theory_96acdb1cce8a64aebc57cb78f7401b63d20fe140.png)
or, as we're used to,
 instead of
instead of 
Stuff
Let  with
with 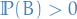 .
.
Then
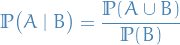
is called the conditional probability of 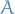 given
given  .
.
Similarily, we define
![\begin{equation*}
\mathbb{E} \big[ X \mid B \big] = \frac{\mathbb{E}[X 1_B]}{\mathbb{P}(B)}
\end{equation*}](../../assets/latex/measure_theory_1e9e33511ea4e04d0d2b93b6e59baf140240ac27.png)
to be the conditional expectation of  given
given  .
.
- Quite restrictive since we require probability of
 to be non-zero
to be non-zero - Goal: improve prediction for
 if additional "information" is available
if additional "information" is available
- "Information" is modelled by a sigma-algebra

- "Information" is modelled by a sigma-algebra
Let  be a sequence of disjoint events, whose union is
be a sequence of disjoint events, whose union is  . Set
. Set

For any integrable random variable  , we can define
, we can define
![\begin{equation*}
Y = \sum_{n \in \mathbb{N}}^{} \mathbb{E} \big[ X \mid B_n \big] 1_{B_n}
\end{equation*}](../../assets/latex/measure_theory_df0b9f2767d97d3a5e3b87e10ea91d7c6a6b2dfa.png)
where we set
![\begin{equation*}
\mathbb{E} \big[ X \mid B_n \big] =
\begin{cases}
\frac{\mathbb{E} [ X 1_{B_n}]}{\mathbb{P}(B_n)} & \text{if } \mathbb{P}(B_n) > 0 \\
0 & \text{if } \mathbb{P}(B_n) = 0
\end{cases}
\end{equation*}](../../assets/latex/measure_theory_cb9ab6ebd3778592daaf856ee81c1ce9ae052dd8.png)
Notice that
 in (discrete) definition of conditional expectation is
in (discrete) definition of conditional expectation is 
![\begin{equation*}
Y(\omega) = \sum_{n \in \mathbb{N}}^{} \mathbb{E} \big[ X \mid B_n \big] 1_{B_n}(\omega)
\end{equation*}](../../assets/latex/measure_theory_de58a386a26a73adfa6a4af4e31476f647bd063e.png)
Let
![$A \in \mathcal{B}([-\infty, \infty])$](../../assets/latex/measure_theory_80ea66eaeaaf042e5dc2c64f20a6b901294f66b1.png) , then
, then
![\begin{equation*}
\begin{split}
Y^{-1}(A) &= \left\{ \omega \in \Omega \mid Y(\omega) \in A \right\} \\
&= \left\{ \omega \in \Omega \mid \sum_{n \in \mathbb{N}}^{} \mathbb{E}[X \mid B_n] 1_{B_n}(\omega) \in A \right\} \\
&= \bigcup_{n \in \mathbb{N}}^{} \left\{ \omega \in B_n \mid \mathbb{E} [X \mid B_n] 1_{B_n}(\omega) \in A \right\}
\end{split}
\end{equation*}](../../assets/latex/measure_theory_ae441ad10a694990770aa1023a1c91c6f5f09304.png)
because
 , and each of these sets are measurable
Notice that this is simply the union of intersections
, and each of these sets are measurable
Notice that this is simply the union of intersections
![\begin{equation*}
B_n \cap \bigcup_{m \in \mathbb{M}: \mathbb{E}[X \mid B_m] = \mathbb{E}[X \mid B_n]}^{} \big( 1_{B_m} \big)^{-1} \big( \left\{ \mathbb{E}[x \mid B_m] \right\} \big)
\end{equation*}](../../assets/latex/measure_theory_a1b0f0540a9b646a48533f484508951c6c830ff5.png)
which is just
![\begin{equation*}
B_n \cap \bigcup_{m \in \mathbb{N}: \mathbb{E}[X \mid B_m] = \mathbb{E}[X \mid B_n]}^{} B_m
\end{equation*}](../../assets/latex/measure_theory_2693613be68d22d64d95c5bbb7a9c8866568fb73.png)
But this is just
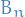 since
since  ! That is,
! That is,
![\begin{equation*}
B_n \cap \bigcup_{m \in \mathbb{N}: \mathbb{E}[X \mid B_m] = \mathbb{E}[X \mid B_n]}^{} B_m = B_n
\end{equation*}](../../assets/latex/measure_theory_04665406f264cd513e186a5c37f64c85b115f355.png)
Which means we end up with
![\begin{equation*}
Y^{-1}(A) = \bigcup_{n \in \mathbb{N} : \mathbb{E}[X \mid B_n] \in A}^{} B_n
\end{equation*}](../../assets/latex/measure_theory_df38087f0a75797fa14a22a0777a5a48f3ebfd04.png)
which is union of
 sets and so
sets and so  is
is  random variable.
random variable.
 is integrable and
is integrable and
![\begin{equation*}
\mathbb{E} \big[ X 1_G \big] = \mathbb{E} \big[ Y 1_G \big], \quad \forall G \in \mathcal{G}
\end{equation*}](../../assets/latex/measure_theory_5ffa11f20c0745066246431ea053cb46f2e0fb28.png)
This is easily seen from
![\begin{equation*}
\begin{split}
\mathbb{E} \big[ \sum_{n \in \mathbb{N}}^{} \mathbb{E}[X \mid B_n] 1_{B_n} 1_G \big] &= \sum_{n \in \mathbb{N}}^{} \mathbb{E}[X \mid B_n] \mathbb{E} \big[ 1_{B_n} 1_G \big] \\
&= \sum_{n \in \mathbb{N}}^{} \mathbb{E}[X \mid B_n] \mathbb{P}(B_n \cap G) \\
&\le \sum_{n \in \mathbb{N}}^{} \mathbb{E}[X \mid B_n] \\
&< \infty
\end{split}
\end{equation*}](../../assets/latex/measure_theory_edb19c0a7d26d19df4af59b92b7e337194286918.png)
since
 and
and  is integrable.
is integrable.
There's an issue with the (discrete) definition of conditional expectation though. Example:
![$\Omega = (0, 1]$](../../assets/latex/measure_theory_9f127db903a6185b432e0d796de91a2244c74c0c.png) ,
, 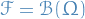 and
and  be the Lebesgue measure
be the Lebesgue measureConsider the case
![\begin{equation*}
\mathcal{G} = \sigma \Bigg( \bigg( \frac{k}{m}, \frac{k + 1}{m} \bigg], k = 0, \dots, m - 1 \Bigg)
\end{equation*}](../../assets/latex/measure_theory_d87a874a937988e58865bc74988ff2fb04317fab.png)
- Then consider
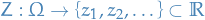 is a rv.
is a rv. Then let

Then
![\begin{equation*}
\begin{split}
\mathbb{E} \big[ X \mid Z \big] &:= \mathbb{E} \big[ X \mid \sigma(Z) \big] \\
&= \sum_{i : \mathbb{P}(\left\{ Z = z_i \right\} > 0)}^{} \mathbb{E} \big[ X \mid \left\{ Z = z_i \right\} \big] 1_{\left\{ Z = z_i \right\}}
\end{split}
\end{equation*}](../../assets/latex/measure_theory_8afa65ef5b58e61621382cd947e6dd378880711e.png)
Issue: if
 has an absolutely continuous distribution, e.g.
has an absolutely continuous distribution, e.g.  , i.e.
, i.e.

then the set we're summing over
 is the empty set!
is the empty set!
- This motivates the more general defintion which comes next!
Let  with
with  is a σ-algebra.
is a σ-algebra.
A random variable  is called (a version of) the conditional expectation of
is called (a version of) the conditional expectation of  given by
given by  if
if
 is
is 
And
![\begin{equation*}
\mathbb{E} \big[ X 1_A \big] = \mathbb{E} \big[ Y 1_A \big], \quad \forall A \in \mathcal{G}
\end{equation*}](../../assets/latex/measure_theory_58c12ca12579b4bd31fc6ed6b90b39bfad1cabf3.png)
So we write ![$Y = \mathbb{E}[X \mid \mathcal{G}]$](../../assets/latex/measure_theory_67ae070910ce75ccb40ed652c8044d459db93777.png)
 can be replaced by
can be replaced by  throughout
throughout- If
 with
with  it suffices to check for all
it suffices to check for all 
If
 with
with  a rv., then
a rv., then ![$\mathbb{E}[X \mid Z] = \mathbb{E}[X \mid \sigma(Z)]$](../../assets/latex/measure_theory_514ce14936cfe3c0331b68c84e6c3b3d678ebab8.png) is
is  by condition (1) in def of conditional expectation, so it's of the form
by condition (1) in def of conditional expectation, so it's of the form  for some function
for some function  ; therefore it's common to define
; therefore it's common to define
![\begin{equation*}
\mathbb{E} \big[ X \mid Z = z \big] = f(z)
\end{equation*}](../../assets/latex/measure_theory_b151b8273ce43f8c7fa2aa4d6f3ec82da4fe9ec7.png)
Let  with
with  a sigma-algebra.
a sigma-algebra.
Then
![$Y = \mathbb{E} \big[ X \mid \mathcal{G} \big]$](../../assets/latex/measure_theory_3e5794f7578c56898b6081c3ba5cc885761cf4dc.png) exists
exists- Any two versions of
![$\mathbb{E} \big[ X \mid \mathcal{G} \big]$](../../assets/latex/measure_theory_3d911aeab828448697fecf48b6239be6ac92d329.png) coincide
coincide 
- Let
 be as in conditional expectation and let
be as in conditional expectation and let  satisfy the conditions in the same def for some
satisfy the conditions in the same def for some  with
with  almost surely.
almost surely.
- Let
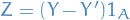 with
with  (in
(in  because both
because both 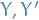 are
are  )
) Then
![\begin{equation*}
\mathbb{E} \big[ Y 1_A \big] = \mathbb{E} \big[ X 1_A \big] \le \mathbb{E} \big[ X' 1_A \big] = \mathbb{E} \big[ Y' 1_A \big] < \infty
\end{equation*}](../../assets/latex/measure_theory_bdd19a2fd99bc9f7d1eb391263eda9b82d22c584.png)
since
 . The first equality is due to condition (2) in def of cond. expectation.
. The first equality is due to condition (2) in def of cond. expectation.
![$\mathbb{E}[Y 1_A] \le \mathbb{E}[Y' 1_A]$](../../assets/latex/measure_theory_b315a1d55ff5a027493a39778b793685622776c3.png) implies, by def of
implies, by def of  , that
, that
![\begin{equation*}
\mathbb{E}[Z] \le 0 \underset{Z \ge 0 \text{ a.s.}}{\implies} Z \overset{\text{a.s.}}{=} 0 \implies Y \overset{\text{a.s.}}{\le} Y'
\end{equation*}](../../assets/latex/measure_theory_af8b973713687db73bedfd09e96d3a22b4559b9c.png)
- If
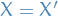 , a similar argument shows that
, a similar argument shows that  (using
(using  and
and  )
)
- The reason why we did the inequality first is because we'll need that later on.
- Let
- We're going to do this by orthogonal projection in
 .
.
Assume
 . Since
. Since 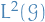 is a complete subspace of
is a complete subspace of  , so such
, so such  has an orthogonal projection
has an orthogonal projection  on
on 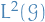 , i.e.
, i.e.
![\begin{equation*}
\exists Y \in L^2(\mathcal{G}) : \quad \mathbb{E} \big[ (X - Y) Z \big] = 0, \quad \forall Z \in L^2(\mathcal{G})
\end{equation*}](../../assets/latex/measure_theory_8896d0ec72f659bf0a0f14d71b74456a31c017a7.png)
Choosing
 for some
for some  , we get
, we get
![\begin{equation*}
\mathbb{E} \big[ X 1_A \big] = \mathbb{E} \big[ Y 1_A \big]
\end{equation*}](../../assets/latex/measure_theory_46d7f25fcb31d3bf5d380e63d35b0ded13de68d2.png)
so
 satisfies (1) and (2) in def of cond expectation, from equation above.
But this is assuming
satisfies (1) and (2) in def of cond expectation, from equation above.
But this is assuming  which is not strict enough for the case when
which is not strict enough for the case when  ! So we gotta do some more work.
! So we gotta do some more work.
Assume
 . Then
. Then  and
and  for some
for some  . By Step 1, we know that
. By Step 1, we know that
![\begin{equation*}
\exists Y_m \in L^2(\mathcal{G}): \quad \mathbb{E} \big[ X_m 1_A \big] = \mathbb{E} \big[ Y_m 1_A \big], \quad \forall A \in \mathcal{G}
\end{equation*}](../../assets/latex/measure_theory_4fe85557d766dbc30be33d7b0fca148e7633f038.png)
and
 a.s. (by proof of (2) above).
Further, let
a.s. (by proof of (2) above).
Further, let

with

which is just the set where the sequence is increasing. Then
 is
is  and by MCT we get
and by MCT we get
![\begin{equation*}
\mathbb{E} \big[ X 1_A \big] = \mathbb{E} \big[ Y_{\infty} 1_A \big]
\end{equation*}](../../assets/latex/measure_theory_4c9e6258d1ec98924d1b8cf00378d4e89ef6bf10.png)
Then, letting
 ,
,
![\begin{equation*}
\underset{A = \Omega}{\implies} \mathbb{E}[Y_{\infty}] = \mathbb{E}[X] \underset{X \in L^1}{<} \infty
\end{equation*}](../../assets/latex/measure_theory_aa5c1ebe8c9a47a0a14822f65863937bc9156ad0.png)
so
 a.s. (and thus
a.s. (and thus  ) and
) and

satisfies the condtions in def of cond expectation
For general
 , apply Step 2 on
, apply Step 2 on  and
and  to obtain
to obtain  and
and  . Then
. Then

satisfies the condtions in def of cond expectation.
Let  , i.e. integrable random variable, and let
, i.e. integrable random variable, and let  be a σ-algebra.
be a σ-algebra.
We have the following properties:
![$\mathbb{E} \big[ \mathbb{E}[X \mid \mathcal{G}] \big] = \mathbb{E}[X]$](../../assets/latex/measure_theory_b14b07e854cdd765efad83ceb2d2280e02ec899d.png)
- If
 is
is  , then
, then ![$\mathbb{E}[X \mid \mathcal{G}] \overset{\text{a.s.}}{=} X$](../../assets/latex/measure_theory_fa97a9f2f107a062bb6f5e4c0e65d02bb208342c.png)
- If
 is independent of
is independent of  , then
, then ![$\mathbb{E}[X \mid \mathcal{G}] \overset{\text{a.s.}}{=} \mathbb{E}[X]$](../../assets/latex/measure_theory_1a492266028a6b7630c03206584471cd5c07473d.png)
- If
 , then
, then ![$\mathbb{E}[X \mid \mathcal{G}] \overset{a.s.}{\ge} 0$](../../assets/latex/measure_theory_5c0c761d80d5e2d00e61dc56b7d32faec224c43e.png) .
. For
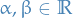 and any integrable random variable
and any integrable random variable  , we have
, we have
![\begin{equation*}
\mathbb{E} \big[ \alpha X + \beta Y \mid \mathcal{G} \big] \overset{\text{a.s.}}{=} \alpha \mathbb{E} [X \mid \mathcal{G}] + \beta \mathbb{E}[Y \mid \mathcal{G}]
\end{equation*}](../../assets/latex/measure_theory_0ceb320fe1a686e88594a6b185caef5f514c147b.png)
Let  be a sequence of random variables. Suppose further
be a sequence of random variables. Suppose further  a.s., then
a.s., then ![$\mathbb{E}[X_n \mid \mathcal{G}] \uparrow Y$](../../assets/latex/measure_theory_ebd7e1e3f48913ca0c2cb384d82d2be903011ff4.png) a.s., for some
a.s., for some  random variable
random variable  .
.
(conditional MCT) By MCT, we therefore have
![\begin{equation*}
\mathbb{E} [X 1_A] = \lim_{n \to \infty} \mathbb{E}[X_n 1_A] = \lim_{n \to \infty} \mathbb{E} \big[ \mathbb{E}[X_n \mid \mathcal{G}] 1_A \big] = \mathbb{E}[Y 1_A], \quad \forall A \in \mathcal{G}
\end{equation*}](../../assets/latex/measure_theory_da5eb05e97e04778ae58b3f8a5a3b2ad7646f58c.png)
which implies that
![\begin{equation*}
Y \overset{\text{a.s.}}{=} \mathbb{E}[X \mid \mathcal{G}]
\end{equation*}](../../assets/latex/measure_theory_4c4a483287139468645db3e20117474247c63466.png)
This is basically the conditional MCT:
![\begin{equation*}
0 \le X_n \uparrow X \text{ a.s. } \quad \implies \quad \mathbb{E}[X_n \mid \mathcal{G}] \uparrow \mathbb{E}[X \mid \mathcal{G}] \text{ a.s.}
\end{equation*}](../../assets/latex/measure_theory_e2781911c713583c13dd91a8dc8a07c2313efb6d.png)
(conditional Fatou's lemma)
![\begin{equation*}
X_n \ge 0, \quad \forall n \in \mathbb{N} \quad \implies \quad \mathbb{E} [\liminf_{n \to \infty} X_n \mid \mathcal{G}] \overset{a.s.}{\le} \liminf_{n \to \infty} \mathbb{E}[X_n \mid \mathcal{G}]
\end{equation*}](../../assets/latex/measure_theory_7170c8c44f645d75511e7f60a290595e826dee78.png)
(conditional Dominated convergence) If
 and
and  for all
for all  , almost surely, for some integrable variable
, almost surely, for some integrable variable  , then
, then
![\begin{equation*}
\mathbb{E}[X_n \mid \mathcal{G}] \overset{a.s.}{\to} \mathbb{E}[X \mid \mathcal{G}]
\end{equation*}](../../assets/latex/measure_theory_2299cb2a8c7408334e50c537874a058800f25354.png)
(conditional Jensen's inequality) If
![$c: \mathbb{R} \to (-\infty, \infty]$](../../assets/latex/measure_theory_0fbf01fc0b204736d63b072e13cefceee1e07280.png) is convex, then
is convex, then
![\begin{equation*}
\mathbb{E} \big[ c(X) \mid \mathcal{G} \big] \overset{a.s.}{\ge} c \big( \mathbb{E}[X \mid \mathcal{G}] \big)
\end{equation*}](../../assets/latex/measure_theory_8e771661f8b3add562a74e9c7dfcd7ecb6d7b37d.png)
In particular, for
 , we have
, we have
![\begin{equation*}
\norm{\mathbb{E}[X \mid \mathcal{G}]_p^p} = \mathbb{E} \big[ \left| \mathbb{E}[X \mid \mathcal{G}] \right|^p \big] \le \mathbb{E} \big[ \mathbb{E}[\left| X \right|^p \mid \mathcal{G}] \big] = \mathbb{E} \big[ \left| X \right|^p \big] = \norm{X}_p^p
\end{equation*}](../../assets/latex/measure_theory_92588444125acc4be617da160afc554841828f69.png)
where we used Jensen's inequality for the inequality. Thus we have
![\begin{equation*}
\norm{\mathbb{E}[X \mid \mathcal{G}]}_p \le \norm{X}_p, \quad \forall \ 1 \le p < \infty
\end{equation*}](../../assets/latex/measure_theory_464b507208c6365b57576104255b55018d0b18f0.png)
For any σ-algebra  , the rv.
, the rv. ![$Y = \mathbb{E} \big[ \mathbb{E}[X \mid \mathcal{G}] \mid \mathcal{H} \big]$](../../assets/latex/measure_theory_a332812e3fce8c10c80fa3a9f640001016705f8e.png) is
is  and satisfies, for all
and satisfies, for all  ,
,
![\begin{equation*}
\mathbb{E} \big[ Y 1_A \big] = \mathbb{E} \big[ \mathbb{E}[X \mid \mathcal{G}] 1_A \big] = \mathbb{E}[X 1_A]
\end{equation*}](../../assets/latex/measure_theory_6144fe4dcd295a073ccaab093d7bd52be3094166.png)
(Tower property)
![\begin{equation*}
\mathcal{H} \subseteq \mathcal{G} \quad \implies \quad \mathbb{E} \big[ \mathbb{E}[X \mid \mathcal{G}] \mid \mathcal{H} \big] \overset{\text{a.s.}}{=} \mathbb{E}[X \mid \mathcal{H}]
\end{equation*}](../../assets/latex/measure_theory_edb1f9de8eca8a64e3a7c3a4b2aefc6f83eb02d2.png)
"Take out what is known": if
 is bounded and
is bounded and  , then
, then
![\begin{equation*}
\mathbb{E}[Y X \mid \mathcal{G}] = Y \mathbb{E}[X \mid \mathcal{G}]
\end{equation*}](../../assets/latex/measure_theory_2eda6d4883938a3ab1adc25c5ada1a67c3ed2e9b.png)
since
 is then
is then  and
and
![\begin{equation*}
\mathbb{E} \big[ 1_A \mathbb{E}[YX \mid \mathcal{G}] \big] \overset{\text{a.s.}}{=} \mathbb{E} [ 1_A YX ] = Y \mathbb{E}[1_A X] \overset{\text{a.s.}}{=} Y \mathbb{E} \big[ 1_A \mathbb{E}[X \mid \mathcal{G}] \big], \quad \forall A \in \mathcal{G}
\end{equation*}](../../assets/latex/measure_theory_2409ce4aed93c643b2b12d4ec929ab363456c509.png)
(actually, you need to first consider
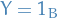 for some
for some  , and then extend to all measurable functions
, and then extend to all measurable functions  using simple functions as usual)
using simple functions as usual)
If
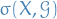 is independent of
is independent of  , then
, then
![\begin{equation*}
\mathbb{E} \big[ X \mid \sigma(\mathcal{G}, \mathcal{H}) \big] \overset{\text{a.s.}}{=} \mathbb{E}[X \mid \mathcal{G}]
\end{equation*}](../../assets/latex/measure_theory_cb1b131dc838e7664f386d4a40506116e0e856e7.png)
Because suppose
 and
and  , then
, then
![\begin{equation*}
\begin{split}
\mathbb{E} \big[ \mathbb{E}[X \mid \sigma(\mathcal{G}, \mathcal{H})] 1_{A \cap B} \big] & =\mathbb{E} \big[ X 1_{A \cap B} \big] \\
&= \mathbb{E} \big[ \mathbb{E}[X \mid \mathcal{G}] 1_A \big] \mathbb{P}(B) \\
&= \mathbb{E} \big[ \mathbb{E}[X \mid \mathcal{G}] 1_{A \cap B} \big]
\end{split}
\end{equation*}](../../assets/latex/measure_theory_7c77cadd4c42d62a0074e23b8ff73783f10ff4fe.png)
The set of such intersections
 is a π-system generating
is a π-system generating  , so the desired formula follows from [SOME PROPOSITION].
, so the desired formula follows from [SOME PROPOSITION].
From defintion of conditional expectation we know that
![\begin{equation*}
\mathbb{E} \big[ \mathbb{E}[X \mid \mathcal{G}] 1_A \big] = \mathbb{E} \big[ X 1_A \big], \quad \forall A \in \mathcal{G}
\end{equation*}](../../assets/latex/measure_theory_6ea29c82e9cfd3d9a9a645324f6660cf63cd30a1.png)
And since
 , we must also have
, we must also have
![\begin{equation*}
\mathbb{E} \big[ \mathbb{E}[X \mid \mathcal{G}] \big] = \mathbb{E} \big[ X \big]
\end{equation*}](../../assets/latex/measure_theory_9abb966b72e1aaabc2e61079b08982090e5072d7.png)
Let
 \ne X(\omega) \right\}$](../../assets/latex/measure_theory_9ce9d3c336faa7b1fa476906d57785e8dd952128.png) . Observe that
. Observe that  since
since
}_{\in \mathcal{B}([-\infty, \infty])} \cap \underbrace{X(\Omega)}_{\in \mathcal{B}([-\infty, \infty])} \Big)^c \in \mathcal{B}([-\infty, \infty])
\end{equation*}](../../assets/latex/measure_theory_1832da8a41b8df322966732d09685d18b5e10671.png)
and both
![$\mathbb{E}[X \mid \mathcal{G}]$](../../assets/latex/measure_theory_85a350ffd2a11f2402d03fa9f54e98334381e887.png) and
and  are
are  , thus the their preimages must be in
, thus the their preimages must be in  and
and
![\begin{equation*}
A = \big( \mathbb{E}[X \mid \mathcal{G}] \big)^{-1}(E) \cup X^{-1}(E) \in \mathcal{G}
\end{equation*}](../../assets/latex/measure_theory_0589da513b10f2233deb717cec68e7d8c708bca8.png)
Moreover, from the definition of
![$\mathbb{E}[X \mid \mathcal{G}]$](../../assets/latex/measure_theory_85a350ffd2a11f2402d03fa9f54e98334381e887.png) , we know that
, we know that
![\begin{equation*}
\mathbb{E} \big[ X 1_A \big] = \mathbb{E} \big[ \mathbb{E}[X \mid \mathcal{G}] 1_A \big]
\end{equation*}](../../assets/latex/measure_theory_e90422e1c07cac278afc6c0ed44fb6452a724385.png)
which implies

i.e.
![\begin{equation*}
X \overset{\text{a.s.}}{=} \mathbb{E}[X \mid \mathcal{G}]
\end{equation*}](../../assets/latex/measure_theory_04c7dc35cf6013f0e6d40fa962bd6baef54c3263.png)
[TODO]
 being independent of
being independent of  means that
means that
![\begin{equation*}
\mathbb{P}(X^{-1}(E) \cap A) = \mathbb{P}\big(X^{-1}(E)\big) \mathbb{P}(A), \quad \forall E \in \mathcal{B}([-\infty, \infty]), \quad \forall A \in \mathcal{G}
\end{equation*}](../../assets/latex/measure_theory_eae1f8d893e0c25b56497d482665aa36ce55d54f.png)
Let
![\begin{equation*}
B := \left\{ \omega \in \Omega \mid \mathbb{E}[X \mid \mathcal{G}] \ne \mathbb{E}[X] \right\} = \mathbb{E}[X \mid \mathcal{G}]^{-1} \big( \left\{ \mathbb{E}[X] \right\} \big) \in \mathcal{G}
\end{equation*}](../../assets/latex/measure_theory_865bf533a8d2179c2955604041a8b99262ce6161.png)
since
![$\mathbb{E}[X \mid \mathcal{G}]$](../../assets/latex/measure_theory_85a350ffd2a11f2402d03fa9f54e98334381e887.png) is
is  .
Then
.
Then
![\begin{equation*}
\mathbb{E} \big[ \mathbb{E}[X \mid \mathcal{G}] 1_B \big] = \mathbb{E} [X 1_B]
\end{equation*}](../../assets/latex/measure_theory_f39a289ad323b303d5b1fa220d55982474ee36d0.png)
by def of expectation. But
![\begin{equation*}
\mathbb{E}[X 1_B] = \int_{X^{-1}(\mathbb{R}) \cap B} X(\omega) \mathbb{P}(\dd{\omega}) \le \Big( \sup_{\omega \in X^{-1}(\mathbb{R}) \cap B} X(\omega) \Big) \mathbb{P}\big(X^{-1}(\mathbb{R}) \cap B \big) = \Big( \sup_{\omega \in X^{-1}(\mathbb{R}) \cap B} X(\omega) \Big) \underbrace{\mathbb{P}\big(X^{-1}(\mathbb{R})\big)}_{= 1} \mathbb{P}(B)
\end{equation*}](../../assets/latex/measure_theory_6aff46543c33e833bda5deac7c7d402181e28434.png)
- Proven in proof:1.4.-lec-existence-and-uniqueness-of-conditional-expectation
If we can show that properties (1) and (2) from def:conditional-expectation is satisfied by
![$\alpha \mathbb{E}[X \mid \mathcal{G}] + \beta \mathbb{E}[Y \mid \mathcal{G}]$](../../assets/latex/measure_theory_e39ca8370a30f8f2b88e574cda1152d47b0ab06c.png) , then by (2) we get LHS immediately.
Measurability follows from linear combination of measurables being measurable. And observe that for all
, then by (2) we get LHS immediately.
Measurability follows from linear combination of measurables being measurable. And observe that for all 
![\begin{equation*}
\begin{split}
\mathbb{E} \big[ (\alpha \mathbb{E}[X \mid \mathcal{G}] + \beta \mathbb{E}[Y \mid \mathcal{G}]) 1_A \big] &= \mathbb{E} \big[ \alpha \mathbb{E}[X \mid \mathcal{G}] 1_A + \beta \mathbb{E}[Y \mid \mathcal{G}] 1_A \big] \\
&= \alpha \mathbb{E} \big[ \mathbb{E}[X \mid \mathcal{G}] 1_A \big] + \beta \mathbb{E} \big[ \mathbb{E}[Y \mid \mathcal{G}] 1_A \big] \\
&= \alpha \mathbb{E} [X 1_A] + \beta \mathbb{E}[Y 1_A] \\
&= \mathbb{E}[(\alpha X + \beta Y) 1_A]
\end{split}
\end{equation*}](../../assets/latex/measure_theory_027e40ced772a4eb9a585f101a78ecc62bffc4fb.png)
by the fact that
![$\mathbb{E}[X \mid \mathcal{G}]$](../../assets/latex/measure_theory_85a350ffd2a11f2402d03fa9f54e98334381e887.png) and
and ![$\mathbb{E}[Y \mid \mathcal{G}]$](../../assets/latex/measure_theory_aabed24a4510e30389ec9bc8f19f3a9f3509c809.png) are both
are both  .
.
Let  . Then the set of random variables
. Then the set of random variables  of the form
of the form
![\begin{equation*}
Y = \mathbb{E}[ X \mid \mathcal{G}]
\end{equation*}](../../assets/latex/measure_theory_934170d3276903877c58696d9c5f1d6786180970.png)
where  is a σ-algebra is uniformly integrable.
is a σ-algebra is uniformly integrable.
Given  , we can find
, we can find  so that
so that
![\begin{equation*}
A \in \mathcal{F} : \mathbb{P}(A) \le \delta \quad \implies \quad \mathbb{E} [ \left| X \right| 1_A ] \le \varepsilon
\end{equation*}](../../assets/latex/measure_theory_c63034d14d67202fc9f811fdf605ed168a34abd2.png)
Then choose  so that
so that
![\begin{equation*}
\mathbb{E}[|X|] \le \lambda \delta
\end{equation*}](../../assets/latex/measure_theory_f82abdc8f13a080efa56b7c9d0d4a8bc4fa42285.png)
Suppose ![$Y = \mathbb{E}[X \mid \mathcal{G}]$](../../assets/latex/measure_theory_67ae070910ce75ccb40ed652c8044d459db93777.png) , then
, then ![$|Y| \le \mathbb{E}[\left| X \right| \mid \mathcal{G}]$](../../assets/latex/measure_theory_1f4784a176b008fc1210a8e7e6a543754b0f9532.png) . In particular,
. In particular,
![\begin{equation*}
\mathbb{E}[\left| Y \right|] \le \mathbb{E}[\left| X \right|]
\end{equation*}](../../assets/latex/measure_theory_fc6c3f166386273284e03ff2da803ef06fc4712a.png)
so, by Markov's inequality, we have
![\begin{equation*}
\mathbb{P} \big( \left| Y \right| \ge \lambda \big) \le \frac{\mathbb{E}[\left| Y \right|]}{\lambda} \le \delta
\end{equation*}](../../assets/latex/measure_theory_02028dcf4735fc5a1563da8067bfa3872f190eb5.png)
Then
![\begin{equation*}
\mathbb{E} \big[ \left| Y \right| 1_{\left| Y \right| \ge \lambda} \big] \le \mathbb{E} \big[ \left| X \right| 1_{\left| Y \right| \ge \lambda} \big] \le \varepsilon
\end{equation*}](../../assets/latex/measure_theory_cd993aa8c7e21c90a3b5b49436029e37bfe715a3.png)
Since our choice of  was independent of
was independent of  , we have our proof for any σ-algebra
, we have our proof for any σ-algebra  .
.
Martingales in discrete time
Let 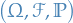 be a probability space.
be a probability space.
A filtration on this space is a sequence  of σ-algebras such that,
of σ-algebras such that,

We also define

Then  .
.
A random process (in discrete time) is a sequence of random variables  .
.
Let  be a random process (discrete time).
be a random process (discrete time).
Then we define the natural filtration of  to be
to be  , given by
, given by

Then  models what we know about
models what we know about  by time
by time  .
.
We say  is adapted to
is adapted to  if
if  is
is  for all
for all  .
.
This is equivalent to requiring that  for all
for all  .
.
Let
 be a filtration
be a filtration
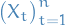 is
is  if
if  is
is  for each
for each ![$t \in [n]$](../../assets/latex/measure_theory_77df7d259c970698dfceec77a36c5d52eec43d96.png) .
.
We say a random process is integrable if  is an integrable random variable for all
is an integrable random variable for all  .
.
A martingale is an adapted random process (discrete time)  such that
such that
![\begin{equation*}
\mathbb{E} \big[ X_{n + 1} \mid \mathcal{F}_n \big] \overset{\text{a.s.}}{=} X_n, \quad \forall n \ge 0
\end{equation*}](../../assets/latex/measure_theory_deae7c487620e3d5e90aa8c282b77d7c9adadbc7.png)
If instead
![\begin{equation*}
\mathbb{E} \big[ X_{n + 1} \mid \mathcal{F}_n \big] \overset{\text{a.s.}}{\le} X_n, \quad \forall n \ge 0
\end{equation*}](../../assets/latex/measure_theory_374dfc453829912cf00bb05259cacf1e7025120c.png)
we say  is a supermartingale.
is a supermartingale.
And if instead
![\begin{equation*}
\mathbb{E} \big[ X_{n + 1} \mid \mathcal{F}_n \big] \overset{\text{a.s.}}{\ge} X_n, \quad \forall n \ge 0
\end{equation*}](../../assets/latex/measure_theory_a53395fc7afac54371a797ed90d1f62ca8abf65a.png)
we say  is a submartingale.
is a submartingale.
Every process which is martingale wrt. a given filtration  is also martingale wrt. its natural filtration.
is also martingale wrt. its natural filtration.
We say a random variable
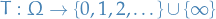
is a stopping time if  for all
for all  .
.
For a stopping time  , we set
, we set

Let  and
and  be stopping times and let
be stopping times and let  be an adapted process. Then
be an adapted process. Then
 is a stopping time
is a stopping time is a σ-algebra
is a σ-algebra- If
 , then
, then 
 is an
is an  random variable
random variable is adapted
is adapted- If
 is integrable, then
is integrable, then  is integrable.
is integrable.
Let
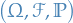 denote a probability space
denote a probability space be a filtration
be a filtration adapted to
adapted to 
Note that
![\begin{equation*}
\left\{ \omega \in \Omega \mid (S \land T)(\omega) \le n \right\} = \Big( S^{-1}\big((-\infty, n]\big) \cap T^{-1} \big( (n, \infty] \big) \Big) \cup \Big( T^{-1}\big((-\infty, n]\big) \cap S^{-1} \big( (n, \infty] \big) \Big)
\end{equation*}](../../assets/latex/measure_theory_9f0b5e61bb3ca6acb613f229b4a5003d08806944.png)
And, since
 and
and  are a stopping times,
are a stopping times,
![$S^{-1} \big( (-\infty, n] \big) \in \mathcal{F}_n$](../../assets/latex/measure_theory_876e244ffc995994312f43b51096e5495b265d11.png) which also implies
which also implies ![$S^{-1} \big( (n, \infty] \big) = \Big( S^{-1} \big( (-\infty, n) \big) \Big)^c$](../../assets/latex/measure_theory_02daa8da8fc73fa0c6c71ac0d20c41806804af30.png) , since a σ-algebra is closed under complements
, since a σ-algebra is closed under complements- Similarily for

- σ-algebra is closed under finite intersections and unions
Hence
![\begin{equation*}
\big( S \land T \big)^{-1} \big( (-\infty, n] \big) \in \mathcal{F}_n
\end{equation*}](../../assets/latex/measure_theory_5619794420586a69c155172af4a10773046bc802.png)
Importantly this holds for all
 , and so
, and so
![\begin{equation*}
(S \land T)^{-1} \big( (-\infty, n] \big) \in \mathcal{F}_n, \quad \forall n \ge 0
\end{equation*}](../../assets/latex/measure_theory_16f3008db5ecd0dae8ddb6199ebbe9ea96890cf4.png)
i.e.
 is a stopping time.
is a stopping time.
Recall

which can equivalently be written
Problem sheets
PS1
1.1
Let  and let
and let  be a σ-algebra. Then
be a σ-algebra. Then
![\begin{equation*}
\mathbb{E}[X + Y \mid \mathcal{G}] \overset{\text{a.s.}}{=} \mathbb{E}[X \mid \mathcal{G}] + \mathbb{E}[Y \mid \mathcal{G}]
\end{equation*}](../../assets/latex/measure_theory_8cf470a61f13927948574342066439e7948c7ba2.png)
First of, ![$\mathbb{E}[X \mid \mathcal{G}] + \mathbb{E}[Y \mid \mathcal{G}]$](../../assets/latex/measure_theory_7620e1fc716c532d2af8cce582694fcae42d78c1.png) is
is  because each
because each ![$\mathbb{E}[X \mid \mathcal{G}]$](../../assets/latex/measure_theory_85a350ffd2a11f2402d03fa9f54e98334381e887.png) and
and ![$\mathbb{E}[Y \mid \mathcal{G}]$](../../assets/latex/measure_theory_aabed24a4510e30389ec9bc8f19f3a9f3509c809.png) are
are  and we know that linear combinations of measurables are measurable.
Second,
and we know that linear combinations of measurables are measurable.
Second,
![\begin{equation*}
\begin{split}
\mathbb{E} \big[ (\mathbb{E}[X \mid \mathcal{G}] + \mathbb{E}[X \mid \mathcal{G}]) 1_A \big] &= \mathbb{E} \big[ \mathbb{E}[X \mid \mathcal{G}] 1_A + \mathbb{E}[Y \mid \mathcal{G}] 1_A \big] \\
&= \mathbb{E} \big[ \mathbb{E}[X \mid \mathcal{G}] 1_A \big] + \mathbb{E} \big[ \mathbb{E}[Y \mid \mathcal{G}] 1_A \big] \\
& \overset{\text{a.s.}}{=} \mathbb{E} [X 1_A] + \mathbb{E}[Y 1_A] \\
&= \mathbb{E} \big[ X 1_A + Y 1_A \big] \\
&= \mathbb{E} \big[ (X + Y) 1_A \big]
\end{split}
\end{equation*}](../../assets/latex/measure_theory_75db366a205975b526e4b88cb86638110241baf9.png)
1.2
Let
 be a non-negative rv.
be a non-negative rv. be a version of
be a version of ![$\mathbb{E}[X \mid \mathcal{G}]$](../../assets/latex/measure_theory_85a350ffd2a11f2402d03fa9f54e98334381e887.png)
Then

i.e.

Further,
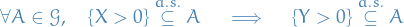
Course: Advanced Financial Models
Notation
Lecture 2
If  is
is  , then
, then 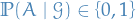 a.s.
a.s.
Conversely, if 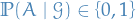 a.s. then
a.s. then 
 s.t
s.t

i.e. everything "interesting" happens in the intersection of 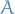 and
and 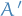
If  then
then
![\begin{equation*}
\begin{split}
\mathbb{P}(A \mid \mathcal{G}) &= \mathbb{E} \big[ 1_A \mid \mathcal{G} \big] \\
&= 1_A \in \left\{ 0, 1 \right\}
\end{split}
\end{equation*}](../../assets/latex/measure_theory_4ee4b85118a52b5e2ac8e67f3c90e080b7396d2e.png)
since  is
is  .
.
Suppose 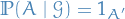 where
where  .
.
Note tthat
![\begin{equation*}
\begin{split}
\mathbb{E} \big[ (1_A - 1_{A'})^2 \big] &= \mathbb{P}(A) + \mathbb{P}(A') - 2 \mathbb{P}(A \cup A') \\
&= 2 \big( \mathbb{P}(A) - \mathbb{P}(A \cap A') \big) \\
&= 0
\end{split}
\end{equation*}](../../assets/latex/measure_theory_399fc3424aa36443a24a97e2ce82bb6edd7dae0a.png)
where in the last equality we've used
![\begin{equation*}
\begin{split}
\mathbb{P}(A \cap A') &= \mathbb{E} \Big[ \mathbb{E} \big[ 1_A - 1_{A'} \mid \mathcal{G} \big] \Big] \\
&= \mathbb{E} \big[ 1_{A'} \mathbb{P}(A \mid \mathcal{G}) \big] \\
&= \mathbb{P}(A') \\
&= \mathbb{P}(A)
\end{split}
\end{equation*}](../../assets/latex/measure_theory_a9c8baa9226f515ae88d9255c4fcf3e574d1228a.png)
 be two finite measures on
be two finite measures on 

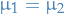


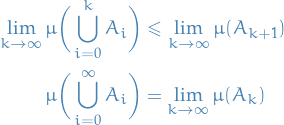
![\begin{equation*}
\sigma \Big( \left\{ A \in \mathcal{A} \mid \exists c \in [- \infty, \infty): X^{-1} \big( (c, \infty] \big) = A \right\} \Big)
\end{equation*}](../../assets/latex/measure_theory_9164c3a0963daefb123e5c34ab8b2b62dc1220b5.png)

![$f: X \to [0, \infty]$](../../assets/latex/measure_theory_975f6cbaae79dc80eb579507ef8e3c7de71d28a6.png) be a nonnegative
be a nonnegative  of
of 
![\begin{equation*}
d \big( [f], [g] \big) = \norm{[f - g]}_{L^1}
\end{equation*}](../../assets/latex/measure_theory_a16835d39d8c52702508e6531de8f45a43dbceb7.png)
 and
and  be finite or
be finite or 
 .
.

 defined by
defined by

![$\mathbb{P}(A \mid \mathcal{G}) = \mathbb{E} \big[ 1_A \mid \mathcal{G} \big]$](../../assets/latex/measure_theory_c23d0999542f850256cae9f7b064df7c745c3fca.png)