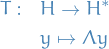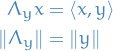Analysis
Table of Contents
Defintions
General
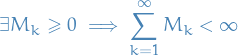
The support of a real-valued function  is given by
is given by

Lp space
 spaces are function spaces defined using a generalization of the p-norm for a finite-dimensional vector space.
spaces are function spaces defined using a generalization of the p-norm for a finite-dimensional vector space.
p-norm
Let  be a real number. Then p-norm (also called the
be a real number. Then p-norm (also called the 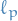 -norm) of vectors
-norm) of vectors 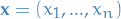 , i.e. over a finite-dimensional vector space, is
, i.e. over a finite-dimensional vector space, is
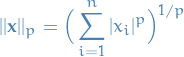
Banach space
A Banach space is a vector space with a metric that:
- Allows computation of vector length and distance between vectors (due to the metric imposed)
- Is complete in the sense that a Cauchy sequence of vectors always converge to a well-defined limit that is within the space
Sequences
Sequences of real numbers
Definition of a convergent sequence

 such that
such that 
 such that
such that 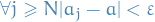
Bounded sequences
A bounded sequence  such that
such that

Cauchy Sequence
A sequence of points  is said to be Cauchy (in
is said to be Cauchy (in  ) if and only if for every
) if and only if for every  there is an
there is an  such that
such that

For a real sequence this is equivalent of convergence.
TODO Uniform convergence
Series of functions
Pointwise convergence
Let  be a nonempty subset of
be a nonempty subset of  . A sequence of functions
. A sequence of functions  is said to converge pointwise on
is said to converge pointwise on  if and only if
if and only if  exists for each
exists for each  .
.
We use the following notation to express pointwise convergence :

Remarks
- The pointwise limit of continuous (respectively, differentiable) functions is not necessarily continuous (respectively, differentiable).
- The pointwise limit of integrable functions is not necessarily integrable.
- There exist differentiable functions
 and
and  such that
such that  pointwise on $[0, 1], but
pointwise on $[0, 1], but
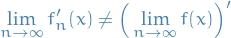
- There exist continuous functions
 and
and  such that
such that  pointwise on $[0, 1] but
pointwise on $[0, 1] but
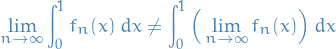
Uniform convergence
Let  be a nonempty subset of
be a nonempty subset of  . A sequence of functions
. A sequence of functions  is said to converge uniformly on
is said to converge uniformly on  to a function
to a function  if and only if for every
if and only if for every  .
.
Continuity
Lipschitz continuity
Given two metric spaces 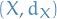 and
and 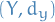 , where
, where 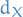 denotes the metric on
denotes the metric on  , and same for
, and same for 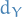 and
and  , a function
, a function  is called Lipschitz continuous if there exists a real constant
is called Lipschitz continuous if there exists a real constant  such that
such that

Where the constant  is referred to as the Lipschitz constant for the function
is referred to as the Lipschitz constant for the function  .
.
If the Lipschitz constant equals one, 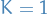 , we say
, we say  is a short-map.
is a short-map.
If the Lipschitz constant  is
is
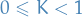
we call the map  a contraction or contraction mapping.
a contraction or contraction mapping.
A fixed point (or invariant point )  of a function
of a function  is an element of the function's domain which is mapped onto itself, i.e.
is an element of the function's domain which is mapped onto itself, i.e.

Observe that if a function  crosses the line
crosses the line 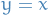 , then it does indeed have a fixed point.
, then it does indeed have a fixed point.
The mean-value theorem can be incredibly useful for checking if a mapping is a contraction mapping, since it states that

for some  .
.
Therefore, if there exists  such that
such that  for all
for all 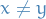 then we clearly know that
then we clearly know that

hence it's a contraction.
Hölder continuity
A real- or complex-valued function  on a d-dimensional Euclidean space is said to satisfy a Hölder condition or is Hölder continuous if there exists non-negative
on a d-dimensional Euclidean space is said to satisfy a Hölder condition or is Hölder continuous if there exists non-negative  and
and  such that
such that

for all  in the domain of
in the domain of  .
.
This definition can easily be generalized to mappings between two different metric spaces.
Observe that if 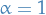 , we have Lipschitz continuity.
, we have Lipschitz continuity.
Càdlàg function
Let 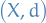 be a metric space, and let
be a metric space, and let  .
.
A function 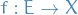 is called a càdlàg function if, for very
is called a càdlàg function if, for very  :
:
The left limit
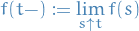
exists.
The right limit
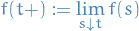
exists and equals

That is,  is right-continuous with left limits.
is right-continuous with left limits.
Affine space
An affine space generalizes the properties of Euclidean spaces in such a way that these are independent of concepts of distance and measure of angles, keeping only properties related to parallelism and ratio of lengths for parallel line segments.
In an affine space, there is no distinguished point that serves as an origin. Hence, no vector has a fixed origin and no vector can be uniquely associated to a point. We instead work with displacement vectors, also called translation vectors or simply translations, between two points of the space.
More formally, it's a set  to which is associated a vector space
to which is associated a vector space  and a transistive and free action
and a transistive and free action  of the additive group of
of the additive group of  . Explicitly, the definition above means that there is a map, generally denoted as an addition
. Explicitly, the definition above means that there is a map, generally denoted as an addition

which has the following properties:
- Right identity: $∀ a ∈ A, a + 0 = 0 $
Associativity:

- Free and transistive action: for every
 , the restriction of the group action to
, the restriction of the group action to  , the induced mapping
, the induced mapping  is a bijection.
is a bijection. - Existence of one-to-one translations: For all
 , the restriction of the group action to
, the restriction of the group action to  , the induced mapping
, the induced mapping  is a bijection.
is a bijection.
This very rigorous definition might seem very confusing, especially I remember finding

to be quite confusing.
"How can you map from some set  to itself when clearly the LHS contains an element from the vector space
to itself when clearly the LHS contains an element from the vector space  !?"
!?"
I think it all becomes apparent by considering the following example:  and
and  . Then, the map
. Then, the map

Simply means that we're using the structure of the vector space 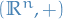 to map an element from
to map an element from 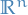 to
to 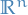 !
!
Could have written

to make it a bit more apparent (but of course, a set does not have any inherit struct, e.g. addition).
Schwartz space
The Schwartz space  is the space of all
is the space of all  functions
functions 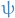 on
on 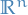 s.t.
s.t.

for all  .
.
Here if 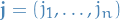 then
then 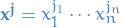 and
and
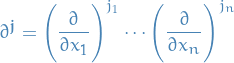
An element of the Schwartz space is called a Schwartz function.
Covering and packing
Let
 be a normed space
be a normed space
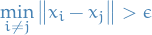
We say a set of points  is an
is an  of
of  if
if
or, equivalently,
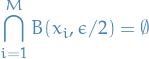
The packing number of  as
as

Theorems
Cauchy's Theorem
This theorem gives us another way of telling if a sequence of real numbers is Cauchy.
Let  be a sequence of real numbers. Then
be a sequence of real numbers. Then  is Cauchy if and only if
is Cauchy if and only if  converges (to some point
converges (to some point  in
in  ).
).
Suppose that  is Cauchy. Given
is Cauchy. Given 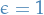 , choose
, choose  such that
such that

By the Triangle Inequality,

Therefore,  is bounded by
is bounded by 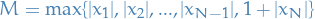 .
.
By the Bolzano-Weierstrass Theorem
Telescoping series

Bolzano-Weierstrass Theorem
A sequence  of sets is said to be nested if
of sets is said to be nested if

If  is a nested subsequence of nonempty bounded intervals, then
is a nested subsequence of nonempty bounded intervals, then

is non-empty (i.e. contains at least one number).
Moreover, if  then
then  contains exactly one number (by non-emptiness of
contains exactly one number (by non-emptiness of  ).
).
Each bounded sequence in 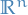 has a convergent subsequence.
has a convergent subsequence.
Assume that  is the lower and
is the lower and  the upper bound of the given sequence. Let
the upper bound of the given sequence. Let ![$I_0 = [a, b]$](../../assets/latex/analysis_16e730a333aaf5ac1faa3b4cef202874f95554ac.png) .
.
Divide  into two halves,
into two halves,  and
and  :
:
![\begin{equation*}
I' = \Bigg[a, \frac{a + b}{2} \Bigg], \quad I'' = \Bigg[ \frac{a + b}{2}, b \Bigg]
\end{equation*}](../../assets/latex/analysis_285aef4cb0f4dc7ec2c3fd6fb02cc01eb8f95f0c.png)
Since  at least one of these intervals contain
at least one of these intervals contain  for infinitively many values of
for infinitively many values of  . We denote the interval with this property
. We denote the interval with this property 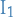 . Let
. Let 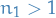 be such that
be such that  .
.
We proceed by induction. Divide the interval  into two halves (like we did with
into two halves (like we did with  ). At least one of the two halves will contain infinitively many
). At least one of the two halves will contain infinitively many  , which we denote
, which we denote  . We choose
. We choose  such that
such that  .
.
Observe that  is a nested subsequence of boudned and closed intervals, hence there exists
is a nested subsequence of boudned and closed intervals, hence there exists  that belongs to every interval
that belongs to every interval  .
.
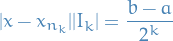
By the Squeeze Theorem  as
as  .
.
Triangle Inequality

Mean Value Theorem
If a function  is continuous on the closed interval
is continuous on the closed interval ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) , and differentiable on the open interval
, and differentiable on the open interval 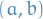 , then there exists a point
, then there exists a point  in
in 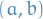 such that:
such that:
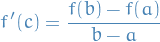
Rolle's Theorem
Suppose  with
with  . If
. If  is continuous on
is continuous on ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) , differentiable on
, differentiable on 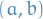 and
and  then
then  for some
for some 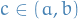 .
.
Intermediate Value Theorem
Consider an interval ![$I = [a, b]$](../../assets/latex/analysis_f5678fa616e44d479ff19a74dbf6956a9abbbf8c.png) on
on  and a continuous function
and a continuous function  . If
. If  is a number between
is a number between  and
and  , then
, then
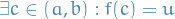
M-test
Let  be a nonempty subset of
be a nonempty subset of  and
and

and suppose
(i.e. series is bounded ).
If  for
for  , then
, then
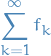
converges absolutely and uniformly on  .
.
Fixed Point Theory
Banach Fixed Point Theorem
Let 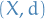 be a be non-empty complete metric space with a contraction mapping
be a be non-empty complete metric space with a contraction mapping  . Then
. Then  admits a unique fixed-point
admits a unique fixed-point  in
in  .
.
Furthermore,  can be found as follows:
can be found as follows:
Start with an arbitrary element  in
in  and define a sequence
and define a sequence  by
by  , then
, then 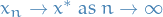
When using this theorem in practice, apparently the most difficult part is to define the domain  such that
such that  .
.
Fundamental Contraction Inequality
By the triangle inequality we have
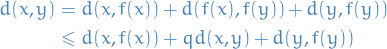
Where we're just using the fact that for any two different  and
and 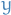 ,
,  is at least less than
is at least less than  by assumption of
by assumption of  being a contraction mapping.
being a contraction mapping.
Solving for  we get
we get
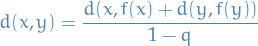
Measure
Definition
A measure on a set is a systematic way of defining a number to each subset of that set, intuitively interpreted as size.
In this sense, a measure is a generalization of the concepts of length, area, volume, etc.
Motivation
The motivation behind defining such a thing is related to the Banach-Tarski paradox, which says that it is possible to decompose the 3-dimensional solid unit ball into finitely many pieces and, using only rotations and translations, reassemble the pieces into two solid balls each with the same volume as the original. The pieces in the decomposition, constructed using the axiom of choice, are non-measurable sets.
Informally, the axiom of choice, says that given a collecions of bins, each containing at least one object, it's possible to make a selection of exactly one object from each bin.
Measure space
If  is a set with the sigma-algebra
is a set with the sigma-algebra  and the measure
and the measure  , then we have a measure space .
, then we have a measure space .
Sigma-algebra
Let  be some set, and let
be some set, and let 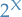 be its power set. Then the subset
be its power set. Then the subset  is a called a σ-algebra on
is a called a σ-algebra on  if it satisfies the following three properties:
if it satisfies the following three properties:

 is closed under complement: if
is closed under complement: if 
 is closed under countable unions: if
is closed under countable unions: if 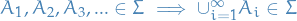
These properties also imply the following:

 is closed under countable intersections: if
is closed under countable intersections: if 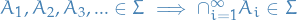
A measure  on a measure space
on a measure space 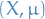 is said to be sigma-finite if
is said to be sigma-finite if  can be written as a countable union of measurable sets of finite measure.
can be written as a countable union of measurable sets of finite measure.
Borel sigma-algebra
Any set in a topological space that can be formed from the open sets through the operations of:
- countable union
- countable intersection
- complement
is called a Borel set.
Thus, for some topological space  , the collection of all Borel sets on
, the collection of all Borel sets on  forms a σ-algebra, called the Borel algebra or Borel σ-algebra .
forms a σ-algebra, called the Borel algebra or Borel σ-algebra .
Borel sets are important in measure theory, since any measure defined on the open sets of a space, or on the closed sets of a space, must also be defined on all Borel sets of that space. Any measure defined on the Borel sets is called a Borel measure.
Lebesgue sigma-algebra
Basically the same as the Borel sigma-algebra but the Lebesgue sigma-algebra forms a complete measure.
- Note to self
Suppose we have a Lebesgue mesaure on the real line, with measure space
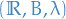 .
.
Suppose that
 is non-measurable subset of the real line, such as the Vitali set. Then the
is non-measurable subset of the real line, such as the Vitali set. Then the 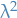 measure of
measure of  is not defined, but
is not defined, but

and this larger set (
 ) does have
) does have 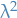 measure zero, i.e. it's not complete !
measure zero, i.e. it's not complete !
- Motivation
Suppose we have constructed Lebesgue measure on the real line: denote this measure space by
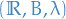 . We now wish to construct some two-dimensional Lebesgue measure
. We now wish to construct some two-dimensional Lebesgue measure 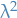 on the plane
on the plane  as a product measure.
as a product measure.
Naïvely, we could take the sigma-algebra on
 to be
to be  , the smallest sigma-algebra containing all measureable "rectangles"
, the smallest sigma-algebra containing all measureable "rectangles"  for
for  .
.
While this approach does define a measure space, it has a flaw: since every singleton set has one-dimensional Lebesgue measure zero,

for any subset of
 .
.
What follows is the important part!
However, suppose that
 is non-measureable subset of the real line, such as the Vitali set. Then the
is non-measureable subset of the real line, such as the Vitali set. Then the 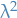 measure of
measure of  is not defined (since we just supposed that
is not defined (since we just supposed that  is non-measurable), but
is non-measurable), but

and this larger set (
 ) does have
) does have 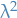 measure zero, i.e. it's not complete !
measure zero, i.e. it's not complete !
- Construction
Given a (possible incomplete) measure space
 , there is an extension
, there is an extension 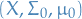 of this measure space that is complete .
of this measure space that is complete .
The smallest such extension (i.e. the smallest sigma-algebra
 ) is called the completion of the measure space.
) is called the completion of the measure space.
It can be constructed as follows:
- Let
 be the set of all
be the set of all  measure zero subsets of
measure zero subsets of  (intuitively, those elements of
(intuitively, those elements of  that are not already in
that are not already in  are the ones preventing completeness from holding true)
are the ones preventing completeness from holding true) - Let
 be the sigma-algebra generated by
be the sigma-algebra generated by  and
and  (i.e. the smallest sigma-algreba that contains every element of
(i.e. the smallest sigma-algreba that contains every element of  and of
and of  )
)  has an extension to
has an extension to  (which is unique if
(which is unique if  is sigma-finite), called the outer measure of
is sigma-finite), called the outer measure of  , given by the infimum
, given by the infimum

Then
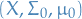 is a complete measure space, and is the completion of
is a complete measure space, and is the completion of  .
.
What we're saying here is:
- For the "multi-dimensional" case we need to take into account the zero-elements in the resulting sigma-algebra due the product between the 1D zero-element and some element NOT in our original sigma-algebra
- The above point means that we do NOT necessarily get completeness, despite the sigma-algebras defined on the sets individually prior to taking the Cartesian product being complete
- To "fix" this, we construct a outer measure
 on the sigma-algebra where we have included all those zero-elements which are "missed" by the naïve approach,
on the sigma-algebra where we have included all those zero-elements which are "missed" by the naïve approach, 
- Let
Product measure
Given two measurable spaces and measures on them, one can obtain a product measurable space and a product measure on that space.
A product measure  is defined to be a measure on the measurable space
is defined to be a measure on the measurable space 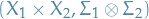 , where we've let
, where we've let  be the algebra on the Cartesian product
be the algebra on the Cartesian product  . This sigma-algebra is called the tensor-product sigma-algebra on the product space.
. This sigma-algebra is called the tensor-product sigma-algebra on the product space.
A product measure  is defined to be a measure on the measurable space
is defined to be a measure on the measurable space 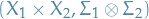 satisfying the property
satisfying the property

Complete measure
A complete measure (or, more precisely, a complete measure space ) is a measure space in which every subset of every null set is measurable (having measure zero).
More formally,  is complete if and only if
is complete if and only if

Lebesgue measure
Given a subset  , with the length of a closed interval
, with the length of a closed interval ![$I = [a,b]$](../../assets/latex/analysis_3fdf3f4bf882725c6261a1b413e5bc0b103e1281.png) given by
given by  , the Lebesgue outer measure
, the Lebesgue outer measure  is defined as
is defined as

The Lebesgue measure is then defined on the Lebesgue sigma-algebra, which is the collection of all the sets  which satisfy the condition that, for every
which satisfy the condition that, for every 

For any set in the Lebesgue sigma-algrebra, its Lebesgue measure is given by its Lebesgue outer measure  .
.
IMPORTANT!!! This is not necessarily related to the Lebesgue integral! It CAN be be, but the integral is more general than JUST over some Lesgue measure.
Intuition
- First part of definition states that the subset
 is reduced to its outer measure by coverage by sets of closed intervals
is reduced to its outer measure by coverage by sets of closed intervals - Each set of intervals
 covers
covers  in the sense that when the intervals are combined together by union, they contain
in the sense that when the intervals are combined together by union, they contain 
- Total length of any covering interval set can easily overestimate the measure of
 , because
, because  is a subset of the union of the intervals, and so the intervals include points which are not in
is a subset of the union of the intervals, and so the intervals include points which are not in 
Lebesgue outer measure emerges as the greatest lower bound (infimum) of the lengths from among all possible such sets. Intuitively, it is the total length of those interval sets which fit  most tightly and do not overlap.
most tightly and do not overlap.
In my own words: Lebesgue outer measure is smallest sum of the lengths of subintervals  s.t. the union of these subintervals
s.t. the union of these subintervals  completely "covers" (i.e. are equivalent to)
completely "covers" (i.e. are equivalent to)  .
.
If you take an a real interval ![$I = [a, b]$](../../assets/latex/analysis_f5678fa616e44d479ff19a74dbf6956a9abbbf8c.png) , then the Lebesge outer measure is simply
, then the Lebesge outer measure is simply  .
.
Lebesgue Integral
The Lebesgue integral of a function  over a measure space
over a measure space  is written
is written

which means we're taking the integral wrt. the measure  .
.

Special case: non-negative real-valued function
Suppose that  is a non-negative real-valued function.
is a non-negative real-valued function.
Using the "partitioning of range of  " philosophy, the integral of
" philosophy, the integral of  should be the sum over
should be the sum over  of the elementary area contained in the thin horizontal strip between
of the elementary area contained in the thin horizontal strip between 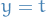 and
and  , which is just
, which is just
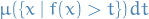
Letting

The Lebesgue integral of  is then defined by
is then defined by
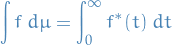
where the integral on the right is an ordinary improper Riemann integral. For the set of measurable functions, this defines the Lebesgue integral.
Measurable function
Let  and
and 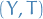 be measurable spaces.
be measurable spaces.
A function  is said to be measurable if the preimage of
is said to be measurable if the preimage of  under
under  is in
is in  for every
for every  , i.e.
, i.e.

Radon measure
- Hard to find a good notion of measure on a topological space that is compatible with the topology in some sense
- One way is to define a measure on the Borel set of the topological space
Let  be a measure on the sigma-algebra of Borel sets of a Hausdorff topological space
be a measure on the sigma-algebra of Borel sets of a Hausdorff topological space  .
.
 is called inner regular or tight if, for any Borel set
is called inner regular or tight if, for any Borel set  ,
,  is the supremum of
is the supremum of 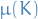 over all compact subsets of
over all compact subsets of  of
of 
 is called outer regular if, for any Borel set
is called outer regular if, for any Borel set  ,
,  is the infimum of
is the infimum of  over all open sets
over all open sets  containing
containing 
 is called locally finite if every point of
is called locally finite if every point of  has a neighborhood
has a neighborhood  for which
for which  is finite (if
is finite (if  is locally finite, then it follows that
is locally finite, then it follows that  is finite on compact sets)
is finite on compact sets)
The measure  is called a Radon measure if it is inner regular and locally finite.
is called a Radon measure if it is inner regular and locally finite.
Suppose  and
and  are two
are two  measures on a measures space
measures on a measures space 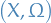 and that
and that  is absolutely continuous wrt.
is absolutely continuous wrt.  .
.
Then there exists a non-negative, measurable function  on
on  such that
such that

The function  is called the density or Radon-Nikodym derivative of
is called the density or Radon-Nikodym derivative of  wrt.
wrt.  .
.
Continuity of measure
Suppose  and
and  are two sigma-finite measures on a measure space
are two sigma-finite measures on a measure space 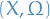 .
.
Then we say that  is absolutely continuous wrt.
is absolutely continuous wrt.  if
if

We say that  and
and  are equivalent if each measure is absolutely continuous wrt. to the other.
are equivalent if each measure is absolutely continuous wrt. to the other.
Density
Suppose  and
and  are two sigma-finite measures on a measure space
are two sigma-finite measures on a measure space 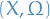 and that
and that  is absolutely continuous wrt.
is absolutely continuous wrt.  . Then there exists a non-negative, measurable function
. Then there exists a non-negative, measurable function  on
on  such that
such that
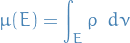
Measure-preserving transformation
 is a measure-preserving transformation is a transformation on the measure-space
is a measure-preserving transformation is a transformation on the measure-space  if
if
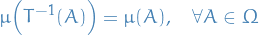
Sobolev space
Notation
 is an open subset of
is an open subset of 
 denotes a infinitively differentiable function
denotes a infinitively differentiable function  with compact support
with compact support is a multi-index of order
is a multi-index of order  , i.e.
, i.e.
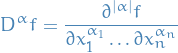
Definition
Vector space of functions equipped with a norm that is a combination of  norms of the function itself and its derivatives to a given order.
norms of the function itself and its derivatives to a given order.
Intuitively, a Sobolev space is a space of functions with sufficiently many derivatives for some application domain, e.g. PDEs, and equipped with a norm that measures both size and regularity of a function.
The Sobolev space spaces  combine the concepts of weak differentiability and Lebesgue norms (i.e.
combine the concepts of weak differentiability and Lebesgue norms (i.e.  spaces).
spaces).
For a proper definition for different cases of dimension of the space  , have a look at Wikipedia.
, have a look at Wikipedia.
Motivation
Integration by parst yields that for every  where
where  , and for all infinitively differentiable functions with compact support
, and for all infinitively differentiable functions with compact support  :
:
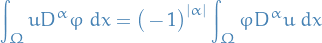
Observe that LHS only makes sense if we assume  to be locally integrable. If there exists a locally integrable function
to be locally integrable. If there exists a locally integrable function  , such that
, such that
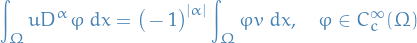
we call  the weak
the weak  -th partial derivative of
-th partial derivative of  . If this exists, then it is uniquely defined almost everywhere, and thus it is uniquely determined as an element of a Lebesgue space (i.e.
. If this exists, then it is uniquely defined almost everywhere, and thus it is uniquely determined as an element of a Lebesgue space (i.e.  function space).
function space).
On the other hand, if  , then the classical and the weak derivative coincide!
, then the classical and the weak derivative coincide!
Thus, if 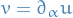 , we may denote it by
, we may denote it by  .
.
Example
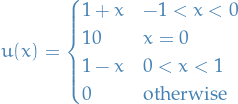
is not continuous at zero, and not differentiable at −1, 0, or 1. Yet the function
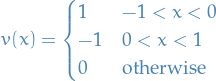
satisfies the definition of being the weak derivative of  , which then qualifies as being in the Sobolev space
, which then qualifies as being in the Sobolev space  (for any allowed
(for any allowed 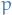 ).
).
Ergodic Theory
Let  be a measure-preserving transformation on a measure space
be a measure-preserving transformation on a measure space  with
with 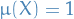 , i.e. it's a probability space.
, i.e. it's a probability space.
Then  is ergodic if for every
is ergodic if for every  we have
we have

Limits of sequences
Infinite Series of Real Numbers
Theorems
Abel's formula
Let  and
and  be real sequences, and for each pair of integers
be real sequences, and for each pair of integers  set
set
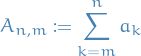
Then
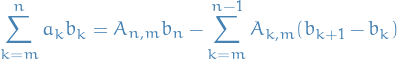
for all integeres  .
.
Since  for
for  and
and  , we have
, we have
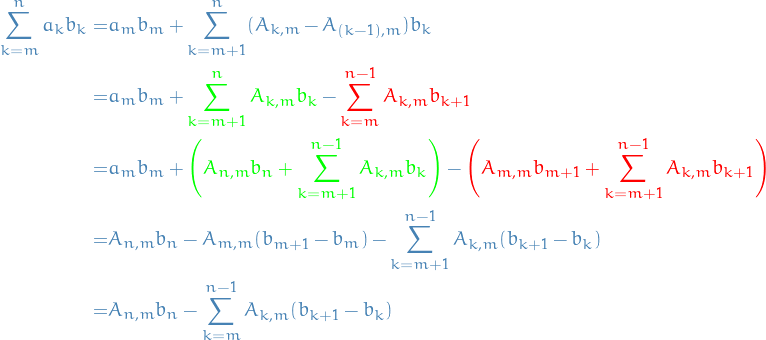
Infinite Series of Functions
Uniform Convergence
Theorems
Cauchy criterion
Let  be a nonempty subset of
be a nonempty subset of  , and let
, and let  be a sequence of functions.
be a sequence of functions.
Then  converges uniformly on
converges uniformly on  if and only if for every
if and only if for every  there is an
there is an  such that
such that

for all  .
.
Generally about uniform convergence
Let  be a nonempty subset of
be a nonempty subset of  and let
and let  be a sequence of real functions defined on
be a sequence of real functions defined on 
i) Suppose that  and that each
and that each  is continuous at
is continuous at  . If
. If  converges uniformly on
converges uniformly on  , then
, then  is continuous at
is continuous at 
ii) [Term-by-term integration] Suppose that ![$E = [a, b]$](../../assets/latex/analysis_b2cd9898000992bba39f8c5b726ba5372034ca64.png) and that each
and that each  is integrable on
is integrable on ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) . If
. If  converges uniformly on
converges uniformly on ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) , then
, then  is integrable on
is integrable on ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) and
and
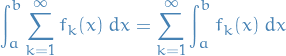
iii) [Term-by-term differentiation] Suppose that  is a bounded, open interval and that each
is a bounded, open interval and that each  is differentiable on
is differentiable on  . If
. If  converges at some
converges at some  , and
, and  converges uniformly on
converges uniformly on  , then
, then  converges uniformly on
converges uniformly on  ,
,  is differentiable on
is differentiable on  , and
, and
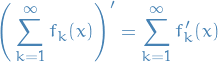
Suppose that  uniformly on a closed interval
uniformly on a closed interval ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) . If each
. If each  is integrable on
is integrable on ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) , then so is
, then so is  and
and
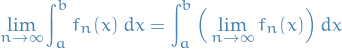
In fact,
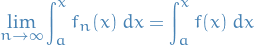
uniformly on ![$x \in [a, b]$](../../assets/latex/analysis_2d517a1540844b320724f283341b89b5a9c92577.png) .
.
Problems
7.2.4
Let
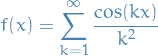

- Show that the series converges on
![$[0, \frac{\pi}{2}]$](../../assets/latex/analysis_2ab3b0e0ae3632b24a23b25b4ec68039f3ab2cad.png)
- We can integrate series term by term
Start by bounding the terms in the sum:
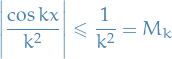
And since the series  converges, the series in question converges.
converges, the series in question converges.
Further,
![\begin{equation*}
\begin{align}
\int_0^{\pi / 2} f(x) dx &= \sum_{k=1}^\infty \int_0^{\pi / 2} \frac{\cos kx}{k^2} \ dx \\
&= \sum_{k=1}^\infty \Big[ \frac{\sin kx}{k^3} \Big]_0^{\pi / 2} \\
&= \sum_{k=1}^\infty \frac{\sin (k \pi / 2)}{k^3}
\end{align}
\end{equation*}](../../assets/latex/analysis_0e8acf3f08bd65d77e0a4a7b036002bf65bb6c6c.png)
Here we note that the numerator will only take on the values 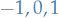 , and in the non-zero cases the denominator will be as in the claim.
, and in the non-zero cases the denominator will be as in the claim.
TODO 7.2.5

converges pointwise on  and uniformly on each bounded interval in
and uniformly on each bounded interval in  to a differentiable function
to a differentiable function  which satisfies
which satisfies

for all 
- Pointwise convergence on

- Uniform convergence
![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) with
with 
For 1. we observe that
![\begin{equation*}
\mathbb{R} = \underset{m \ge 1}{\cup} [ -m, m]
\end{equation*}](../../assets/latex/analysis_6f5476a8bdb9d58f0ea2313913f8e88aaaaa6263.png)
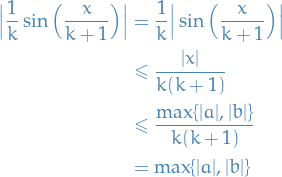
where the last step is due to the sum being a Telescoping series, which equals 1.
We then use the M-test, hence we get convergence in uniform on ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) .
.
Now that we know that the series converges, we need to establish that the function satisfies the boundaries.
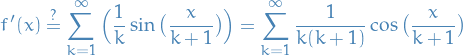
Where  becomes
becomes  if we can prove that RHS converges.
if we can prove that RHS converges.
TODO 7.2.6

- Look at the more general case
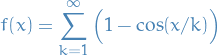
- Look also at

Workshop 2
- 6
- Question
Let
 for
for ![$x \in [0, 1]$](../../assets/latex/analysis_1abcf6a6ba0996351c652ec55b2a137f25774cfc.png) . Prove that
. Prove that  converges pointwise on
converges pointwise on ![$[0, 1]$](../../assets/latex/analysis_68c8fa38d960e53d4308cbf1e65d04c66a554817.png) and find the limit function.
Is the convergence uniform on
and find the limit function.
Is the convergence uniform on ![$[0, 1]$](../../assets/latex/analysis_68c8fa38d960e53d4308cbf1e65d04c66a554817.png) ? Is the convergence uniform on
? Is the convergence uniform on ![$[a, 1]$](../../assets/latex/analysis_cb441010393ff7a0abf0e50800c1ad385443f0ba.png) with
with  ?
?
- Answer
First observe that for
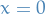 and
and 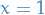 we have
we have

And for
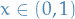

Therefore the limiting function is

Is the convergence uniform on
![$[0, 1]$](../../assets/latex/analysis_68c8fa38d960e53d4308cbf1e65d04c66a554817.png) ? No!
By Thm. 7.10 in introduction_to_analysis we know that if
? No!
By Thm. 7.10 in introduction_to_analysis we know that if  uniformly then
uniformly then
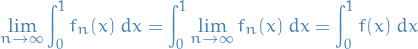
but in this case
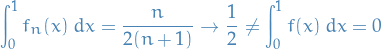
Hence we have a proof by contradiction.
Is the convergence uniform on
![$[a, 1]$](../../assets/latex/analysis_cb441010393ff7a0abf0e50800c1ad385443f0ba.png) ? Yes!
? Yes!
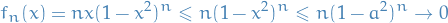
and

hence
 uniformly on
uniformly on ![$[a, 1]$](../../assets/latex/analysis_cb441010393ff7a0abf0e50800c1ad385443f0ba.png) for
for  .
.
- Question
- 7
- Question
Let
 be a sequence of continuous functions which converge uniformly to a function
be a sequence of continuous functions which converge uniformly to a function  . Let
. Let  be a sequence of real numbers which converges to
be a sequence of real numbers which converges to  . Show that
. Show that  .
.
- Answer
Observe that
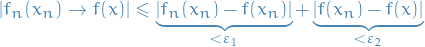
for some
 and
and  . We know
. We know

and for all

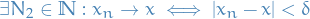
Further, by Theorem 7.10 introduction_to_analysis,

which implies

Therefore, for
 , let
, let
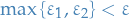
and

then
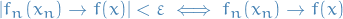
as wanted.
- Question
Uniform Continuity
Theorems
Suppose ![$f: [a, b] \to \mathbb{R}$](../../assets/latex/analysis_ad16c0aff3aa355602aa32a69863fed8f987a882.png) is continuous. Then it is uniformly continuous.
is continuous. Then it is uniformly continuous.
Problems
Workshop 3
- 5
- Question
Let
 be an open interval in
be an open interval in  . Suppose
. Suppose  is differentiable and its derivative
is differentiable and its derivative  is bounded on
is bounded on  . Prove that
. Prove that  is uniformly continuous on
is uniformly continuous on  .
.
- Answer
Suppose
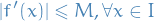
for
 . Then by Mean Value theorem we have
. Then by Mean Value theorem we have

Therefore,
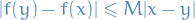
Thus, let
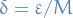
Then

Hence
 is uniformly continuous.
is uniformly continuous.
- Question
Power series
Definitions
Let  be a sequence of real numbers, and
be a sequence of real numbers, and  . A power series is a series of the form
. A power series is a series of the form
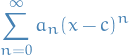
The numbers  are called coefficients and the constant
are called coefficients and the constant  is called the center.
is called the center.
Suppose we have the power series
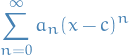
then the radius of convergence  is given by
is given by

unless  is bounded for all
is bounded for all  , in which case we declare
, in which case we declare 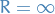
I.e.  is the smallest number such that all series with
is the smallest number such that all series with  is bounded.
is bounded.
Analytic functions
We say a function is analytic if it can be expressed as a power-series .
More precisely,  is analytic on
is analytic on  if there is a power series which converges to
if there is a power series which converges to  on
on  .
.
Theorems

This holds in general , thus is basically another way of defining the radius of convergence .

provided this limit exists.
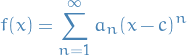
Converges to a continous function
Assume that  . Suppose that
. Suppose that  . Then the power series converges uniformly and absolutely on
. Then the power series converges uniformly and absolutely on  to a continuous function
to a continuous function  . That is,
. That is,
Taylor's Theorem
Suppose the radius of convergence is  . Then the function
. Then the function
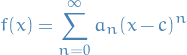
is infinitely differentiable on  , and for such x,
, and for such x,

and the series converges absolutely, and also uniformly on ![$[r - c, r + c]$](../../assets/latex/analysis_153f574aa8dc8898ab42019326f68c167645a08d.png) for any $ r < R$. Moreover
for any $ r < R$. Moreover
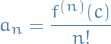
Consider the series
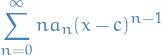
which has radius of convergence  and so converges uniformly on
and so converges uniformly on ![$[r - c, r + c]$](../../assets/latex/analysis_153f574aa8dc8898ab42019326f68c167645a08d.png) for any
for any  .
.
Since
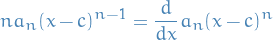
and  at least converges at one point, then by Theorem 7.14 in Wade's we know that
at least converges at one point, then by Theorem 7.14 in Wade's we know that

Further, we have  and
and  , which we can keep on doing and end up with
, which we can keep on doing and end up with

Problems
Finding radius of convergence
The power series
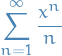
has a radius of convergence 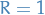 , and converges absolutely on the interval
, and converges absolutely on the interval  .
.
One can easily see that the series convergences on the the interval  , and so we consider the endpoints of this interval.
, and so we consider the endpoints of this interval.
 convergences
convergences , which is known as the harmonic series and is known to diverge
, which is known as the harmonic series and is known to diverge
7.3.1
a)
The series
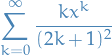
converges on the interval  , and has radius of convergence
, and has radius of convergence 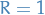 .
.
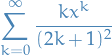
Letting  we write
we write

Using the Ratio test, gives us
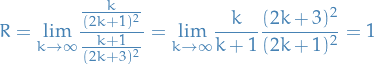
Thus we have the endpoints  and
and  .
.
For 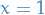 we get the series
we get the series
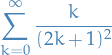
which converges.
For 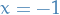 we get the series
we get the series
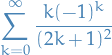
for which we can use the alternating series test to show that it converges.
Thus, we have the series converging on the interval  .
.
b)
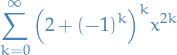
We observe that
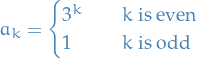
and let  , writing the series as
, writing the series as

and using the root test, we get
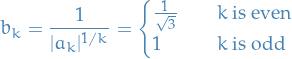
where we let the above equal  for the sake of convenience.
for the sake of convenience.
Then we use the lim-inf definition of radius of convergence
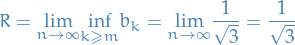
c)
7.3.2
a)
Look at solution to 7.3.1. a)
b)
c)
Integrability on R
Definitions
Partition
Let  with
with 
i) A partition of the interval ![$[a,b]$](../../assets/latex/analysis_bf64a90d032efdc91fa5aab3916a535ed7759bfd.png) is a set of points
is a set of points 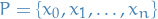 such that
such that

ii) The norm of a partition 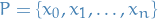 is the number
is the number
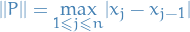
iii) A refinement of a partition 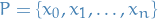 is a partition
is a partition  of
of ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) which satisfies
which satisfies  . In this case we say that
. In this case we say that  is finer than
is finer than  .
.
Riemann sum
Let  with
with  , let
, let  be a partition of the interval
be a partition of the interval ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) , set
, set 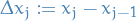 for
for 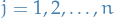 and suppose that
and suppose that ![$f : [a, b] \to \mathbb{R}$](../../assets/latex/analysis_7ae547159e883a60c88d3c5ad37403c18e8f1e01.png) is bounded.
is bounded.
i) The upper Riemann/Darboux sum of  over
over  is the number
is the number
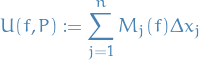
where
![\begin{equation*}
M_j(f) := \sup f([x_{j-1}, x_j]) := \underset{t \in [x_{j-1}, x_j]}{\sup} f
\end{equation*}](../../assets/latex/analysis_a72eb6f326a231e085d67916ecec318f7befc1ec.png)
ii) The lower Riemann/Darboux sum of  over
over  is the number
is the number
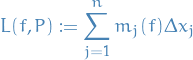
where
![\begin{equation*}
m_j(f) := \inf f([x_{j-1}, x_j]) := \underset{t \in [x_{j-1}, x_j]}{\inf} f
\end{equation*}](../../assets/latex/analysis_87c1f17848cd3a70860929b3794100e042510f95.png)
Since we assumed  to be bounded, the numbers
to be bounded, the numbers  and
and  exist and are finite.
exist and are finite.
Riemann integrable
Let  with
with  . A function
. A function ![$f: [a, b] \to \mathbb{R}$](../../assets/latex/analysis_ad16c0aff3aa355602aa32a69863fed8f987a882.png) is said to be Riemann integrable on
is said to be Riemann integrable on ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) if and only if
if and only if  is bounded on
is bounded on ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) , and for every
, and for every 
![\begin{equation*}
\exists P = \{ x_0, x_1, \dots, x_n \} \text{ of } [a, b] \implies U(f, P) - L(f, P) < \varepsilon
\end{equation*}](../../assets/latex/analysis_9a7a40f41811be0c7486f2ca8192d6274395a41c.png)
I.e. the upper and lower Riemann / Darboux sums has to converge to the same value.
Riemann integral
Let  with
with  , and
, and ![$f : [a, b] \to \mathbb{R}$](../../assets/latex/analysis_7ae547159e883a60c88d3c5ad37403c18e8f1e01.png) be bounded.
be bounded.
i) The upper integral of  on
on ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) is the number
is the number
![\begin{equation*}
(U) \int_a^b f(x) \ dx := \inf \Big\{ U(f, P) : P \text{ is a partition of } [a,b] \Big\}
\end{equation*}](../../assets/latex/analysis_9ca9f18de6839e93d2f409f7705f20e06356e4ab.png)
ii) The lower integral of  on
on ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) is the number
is the number
![\begin{equation*}
(L) \int_a^b f(x) \ dx := \sup \Big\{ L(f, P) : P \text{ is a partition of } [a,b] \Big\}
\end{equation*}](../../assets/latex/analysis_f0eb8f312a92f72970d221f0d051499b877009c0.png)
iii) If the upper and lower integral are equal, we define the integral to be this number
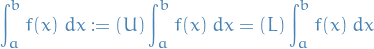
The following definition of the Riemann sum can be proven to be equivalent of the upper and lower integrals using introduction_to_analysis.
Let ![$f : [a, b] \to \mathbb{R}$](../../assets/latex/analysis_7ae547159e883a60c88d3c5ad37403c18e8f1e01.png)
i) A Riemann sum of  wrt. a partition
wrt. a partition 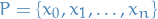 of
of ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) generated by samples
generated by samples ![$t_j \in [x_{j - 1}, x_j]$](../../assets/latex/analysis_4978dc4bc85c39e47478ad104789549be52dc5f5.png) is a sum
is a sum
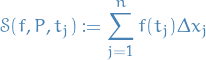
ii) The Riemann sums of  are said to converge to
are said to converge to  as
as  if and only if given
if and only if given  there is a partition
there is a partition  of
of ![$[a ,b]$](../../assets/latex/analysis_565d83a42343e19c30eb852a9ff2cada768b98cb.png) such that
such that

for all choices of ![$t_j \in [x_{j-1}, x_j], j = 1, 2, \dots, n$](../../assets/latex/analysis_a630f0dbcaa3a7c9e0784f856adce66fc9b14c65.png) . In this case we shall use the notation
. In this case we shall use the notation
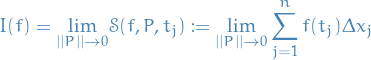 1
1
 is just some arbitrary number in the given interval, e.g. one could set
is just some arbitrary number in the given interval, e.g. one could set  .
.
Theorems
Suppose  with
with  . If
. If  is continuous on the interval
is continuous on the interval ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) , then
, then  is integrable on
is integrable on ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) .
.
Telescoping
If  , then
, then
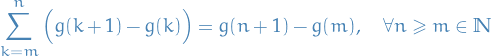
This is more of a remark which is very useful for proofs involving Riemann sums, since we can write
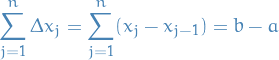
This allows us to write the following inequality for the upper and lower Riemann / Darbaux:

in which case all we need to prove for  to be Riemann integrable is that this goes to zero as
to be Riemann integrable is that this goes to zero as  , or equiv. as we get a finer partition.
, or equiv. as we get a finer partition.
Mean Value Theorem for Integrals
Suppose that  and
and  are integrable on
are integrable on ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) with
with  for all
for all ![$x \in [a, b]$](../../assets/latex/analysis_2d517a1540844b320724f283341b89b5a9c92577.png) . If
. If
![\begin{equation*}
m = \inf f[a, b] \quad \text{and} \quad M = \sup f[a,b]
\end{equation*}](../../assets/latex/analysis_ac26bf0958bb44a3e51160d6c25975bf09116cbc.png)
then
![\begin{equation*}
\exists c \in [a, b] \implies \int_a^b f(x) g(x) \ dx = c \int_a^b g(x) \ dx
\end{equation*}](../../assets/latex/analysis_c5bf5abaf45c5f3d269f0b7cb2da45a15e1cf849.png)
In particular, if  is continuous on
is continuous on ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) , then
, then
![\begin{equation*}
\exists x_0 \in [a,b] \implies \int_a^b f(x) g(x) \ dx = f(x_0) \int_a^b g(x) \ dx
\end{equation*}](../../assets/latex/analysis_b4b547dcefe1725421be04d4d582850664ff7aaa.png)
Suppose that 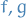 are integrable on
are integrable on ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) , that
, that 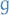 is nonnegative on
is nonnegative on ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) , and that
, and that
![\begin{equation*}
m, M \in \mathbb{R} : m \le \inf f([a, b]) \text{ and } M \ge \sup f([a, b])
\end{equation*}](../../assets/latex/analysis_db75e06669e29f4e9f7940e72c91354c66632f4a.png)
Then there is an ![$c \in [a, b]$](../../assets/latex/analysis_1b6684a4bf25d39ac19401f8f0498e64c814c7db.png) s.t.
s.t.
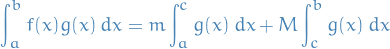
In particular, if  is also nonnegative on
is also nonnegative on ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) , then there is an
, then there is an ![$c \in [a, b]$](../../assets/latex/analysis_1b6684a4bf25d39ac19401f8f0498e64c814c7db.png) which satisifies
which satisifies
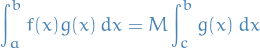
Let  be a real-valued function which is continuous on the closed interval
be a real-valued function which is continuous on the closed interval ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) ,
,  must attain its maximum and minimum at least once. That is,
must attain its maximum and minimum at least once. That is,
![\begin{equation*}
\exists c, d \in [a, b] : f(c) \le f(x) \le f(d), \quad \forall x \in [a, b]
\end{equation*}](../../assets/latex/analysis_9dd84e773a9b779356517ead54f523ee826c7529.png)
Fundamental Theorem of Calculus
Let ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) be non-degenerate and suppose that
be non-degenerate and suppose that ![$f : [a, b] \to \mathbb{R}$](../../assets/latex/analysis_7ae547159e883a60c88d3c5ad37403c18e8f1e01.png) .
.
i) If  is continuous on
is continuous on ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) and
and  , then
, then ![$F \in \mathcal{C}^1 [a, b]$](../../assets/latex/analysis_db8015f30250dd42407ec202a9670eabe00ef24b.png) and
and
![\begin{equation*}
\frac{d}{dx} \int_a^x f(t) \ dt := F'(x) = f(x), \quad \forall x \in [a, b]
\end{equation*}](../../assets/latex/analysis_61fe2abdf6951585784bbe7561466d92248e6c1f.png)
ii) If  is differentiable on
is differentiable on ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) and
and  is integrable on
is integrable on ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) then
then
![\begin{equation*}
\int_a^x f'(t) \ dt = f(x) - f(a), \quad \forall x \in [a,b]
\end{equation*}](../../assets/latex/analysis_00b1ac6ee7d2a71e25da6bbc96aeeb9586e73f6e.png)
Non-degenerate interval means that  .
.
Integrability on R (alternative)
Let  . Then we define the characteristic function
. Then we define the characteristic function
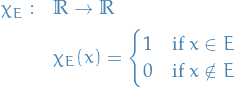
Let  be a bounded interval, then we define the integral of
be a bounded interval, then we define the integral of  as
as
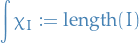
Reminds you about Lebesgue-integral, dunnit?
We say  is a step function if there exist real numbers
is a step function if there exist real numbers

such that
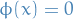 for
for  and
and 
 is constant on
is constant on 
We will use the phrase " is a step function wrt.
is a step function wrt.  " to describe this situation.
" to describe this situation.
In other words,  is step function wrt.
is step function wrt.  iff there exists
iff there exists 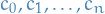 such that
such that
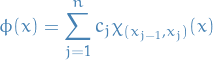
for  .
.
If  is a step function wrt.
is a step function wrt.  which takes the value
which takes the value  on
on  , then
, then
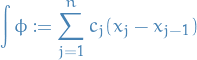
Notice that the values  have no effect on the value of
have no effect on the value of  , as one would expect.
, as one would expect.
Let  . We say that
. We say that  is Riemann integrable if for every
is Riemann integrable if for every  there exist step functions
there exist step functions  and
and  such that
such that

and
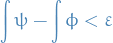
A function  is Riemann integrable if and only if
is Riemann integrable if and only if
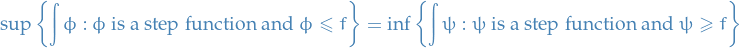
A function  is Riemann integrable if and only if there exist sequences of step functions
is Riemann integrable if and only if there exist sequences of step functions  and
and  such that
such that

and
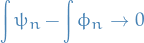
If  and
and  are any sequences of step functions satisfying the above, then
are any sequences of step functions satisfying the above, then

as  .
.
Suppose  and
and 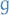 are Riemann integrable, and
are Riemann integrable, and 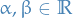 . Then
. Then
 is Riemann-integrable and
is Riemann-integrable and
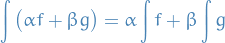
If
 then
then  . Further,
. Further,

 is Riemann integrable and
is Riemann integrable and

 and
and  are Riemann integrable
are Riemann integrable is Riemann integrable
is Riemann integrable
Integrals and uniform limits of sequences and series of functions
Suppose  is a sequence of Riemann integrable functions which
is a sequence of Riemann integrable functions which
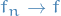
uniformly.
Suppose that  and
and  are zero outside some common interval
are zero outside some common interval ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) . Then
. Then  is Riemann integrable and
is Riemann integrable and
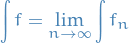
Suppose 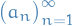 is a non-negative sequence of numbers and
is a non-negative sequence of numbers and  is a function that
is a function that
For some
 and
and 

For
 we have
we have

Then
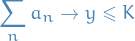
for some  .
.
Problems
Workshop 5
5
- Question
- Answer
 is Riemann integrable, then there exists step-functions
is Riemann integrable, then there exists step-functions  and
and 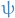 such that
such that

Or rather, for all
 , there exists
, there exists  such that
such that
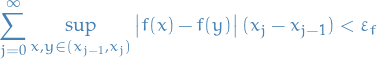
Since
 is integrable on a bounded and closed interval, then
is integrable on a bounded and closed interval, then  is bounded and has bounded support. That is
is bounded and has bounded support. That is
![\begin{equation*}
\sup_{x \in [a, b]} f(x) \le M
\end{equation*}](../../assets/latex/analysis_6c0719e3cc514f0ab23b33fcc394f47c9ab3a7cd.png)
Therefore, by the Mean Value theorem, we have
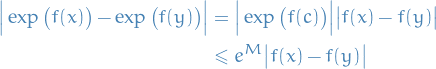
Therefore the "integral sum" for
![$\exp(f) \chi_{[a, b]}$](../../assets/latex/analysis_f4b888411df0037a7c7a441b14f369ad28eab071.png) satisfy the following inequality
satisfy the following inequality
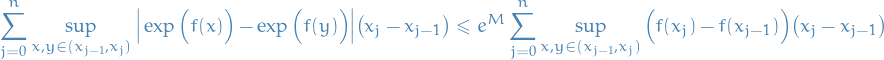
Therefore, for
 , we choose
, we choose
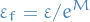
which gives us
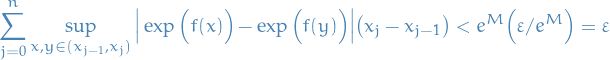
That is,
 is Riemann integrable implies
is Riemann integrable implies ![$\exp(f) \chi_{[a, b]}$](../../assets/latex/analysis_f4b888411df0037a7c7a441b14f369ad28eab071.png) is Riemann integrable.
is Riemann integrable.
We've left out the
![$\chi_{[a, b]}$](../../assets/latex/analysis_bd5a94be38efcaba769bf7a0cc41cb99d3f72501.png) in all the expressions above for brevity, but they ought to be included in a proper treatment.
in all the expressions above for brevity, but they ought to be included in a proper treatment.
Metric spaces
Definitions
Metric
A metric space is a set  together with a function
together with a function  (called the metric of
(called the metric of  ) which satisfies the following properties for all
) which satisfies the following properties for all 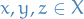 :
:
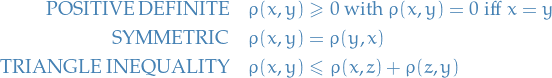 2
2
Metric space
A metric space is a set  together with a function
together with a function  (called the metric of
(called the metric of  ) which satisfies the following properties for all
) which satisfies the following properties for all 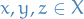 :
:
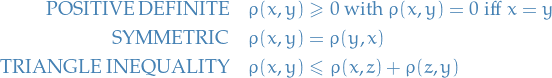 3
3
Balls
Let  and
and  . The open ball (in
. The open ball (in  ) with center
) with center  and radius
and radius  is the set
is the set
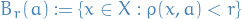
Let  and
and  . The closed ball (in
. The closed ball (in  ) with center
) with center  and radius
and radius  is the set
is the set
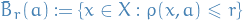
Equivalence of metrics
We say two metrics  and
and  on a set
on a set  are strongly equivalent if and only if
are strongly equivalent if and only if

We say two metrics  and
and  on a set
on a set  are equivalent if and only if for every
are equivalent if and only if for every  and every
and every  there exists
there exists  such that
such that
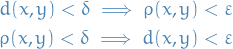
Closedness and openness
Closure and interior
For 
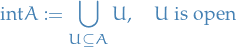
is the interior of  ; it is the largest subset of
; it is the largest subset of  which is open.
which is open.
Or equivalently, the interior of a subset  of points of a topological space
of points of a topological space  consists of all points of
consists of all points of  that do not belong to the boundary of
that do not belong to the boundary of  .
.
A point that is in the interior of  is an interior point of
is an interior point of  .
.
For 
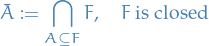
is the closure of  ; it is the smallest set containing
; it is the smallest set containing  which is closed .
which is closed .
Or, equivalently, the closure of  is the union of
is the union of  and all its limit points (points "arbitrarily close to
and all its limit points (points "arbitrarily close to  "):
"):

For 

is the boundary of  .
.
Convergence, Cauchy sequences and completeness
Most theorems and definitions used for sequences are readily generalized to metric spaces.
We say a metric space is complete if and only if every Cauchy sequence in  converges.
converges.
In a metric space  , a sequence
, a sequence  with
with  is bounded if there exists some ball
is bounded if there exists some ball  such that
such that 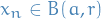 for all
for all  .
.
In a metric space 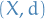 , a sequence
, a sequence  with
with  is a Cauchy sequence iff for every
is a Cauchy sequence iff for every  ,
,

Let 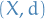 be a metric space, then
be a metric space, then 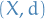 is said to satisfy the Bolzano-Weierstrass Property iff every bounded sequence
is said to satisfy the Bolzano-Weierstrass Property iff every bounded sequence  has a convergent subsequence .
has a convergent subsequence .
Closedness, limit points, cluster points and completeness
 is a limit point for
is a limit point for  if and only if there is a sequence
if and only if there is a sequence 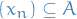 such that
such that  as
as  .
.
 is a cluster point for
is a cluster point for  if and only if every open ball centred at
if and only if every open ball centred at  contains infinitely many points of
contains infinitely many points of  .
.
The following statements are equivalent:
 s a cluster point for
s a cluster point for 
- for all
 ,
,  contains a point of
contains a point of 
 , with
, with  for all
for all  , s.t.
, s.t.  as
as 
Every cluster point for  is a limit point for
is a limit point for  . But
. But  can be a limit point for
can be a limit point for  without being a cluster point .
without being a cluster point .
A closed subset of a complete metric space is complete
A complete subset of any metric space is closed.
Every convergent sequence is Cauchy, but the opposite is not necessarily true.
Compactness
Let 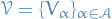 be a collection of subsets of a metric space
be a collection of subsets of a metric space  and suppose that
and suppose that  is a subset of
is a subset of  .
.
 is said to cover
is said to cover  if and only if
if and only if

 is said to be an open covering of
is said to be an open covering of  iff
iff  covers
covers  and each
and each 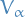 is open.
is open.
Let  be a covering of
be a covering of  .
.
 is said to a finite (respectively, countable ) subcovering iff there is a finite (respectively, countable) subset
is said to a finite (respectively, countable ) subcovering iff there is a finite (respectively, countable) subset  of
of  s.t.
s.t.  covers
covers  .
.
Let 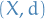 be a metric space.
be a metric space.
A subset  is compact iff for every open cover
is compact iff for every open cover  of
of  , there is a finite subcover
, there is a finite subcover  of
of  .
.
I often find myself wondering "what's so cool about this compactness?! It shows up everywhere, but why?"
Well, mainly it's just a smallest-denominator of a lot of nice properties we can deduce about a metric space. Also, one could imagine compactness being important since the basis building blocks of Topology is in fact open sets, and so by saying that any open cover has a finite open subcover, we're saying it can be described using "finite topological constructs". But honestly, I'm still not sure about all of this :)
One very interesting theorem which relies on compactness is Stone-Weierstrass theorem, which allows us to show that for example polynomials are dense in the space of continous functions! Suuuuper-important when we want to create an approximating function.
Let 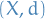 be a metric space and let
be a metric space and let  . Then
. Then  is said to be dense in
is said to be dense in  if for every
if for every  and for every
and for every  we have that
we have that 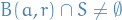 i.e., every open ball in
i.e., every open ball in 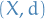 contains a point of
contains a point of  .
.
Or, alternatively, as described in thm:dense-iff-closure-eq-superset:
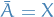
A metric space  is said to be separable iff it contains a countable dense subset.
is said to be separable iff it contains a countable dense subset.
Where with countable dense subset we simply mean a dense subset which is countable.
We say the metric space 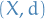 is a precompact metric space if for every
is a precompact metric space if for every  there is a cover of
there is a cover of  by finitely many closed balls of the form
by finitely many closed balls of the form
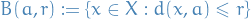
Let  be a complete metric space and precompact, then
be a complete metric space and precompact, then  is compact.
is compact.
Let  be a metric space. Then
be a metric space. Then  is said to be sequentially compact if and only if every sequence in
is said to be sequentially compact if and only if every sequence in  has a convergent subsequence.
has a convergent subsequence.
Let  be a topological space, and
be a topological space, and  a subspace.
a subspace.
Then  is compact (as a topological space with subspace topology) if and only if every cover of
is compact (as a topological space with subspace topology) if and only if every cover of  by open subsets of
by open subsets of  has a finite subcover.
has a finite subcover.
If  for
for  open in
open in  (subspace topology), then
(subspace topology), then 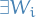 open in
open in  s.t.
s.t.  .
.
Therefore

 : Choose finite subcover
: Choose finite subcover  . Then
. Then  is a finite subcover of
is a finite subcover of  .
.
 : Let
: Let  , then
, then 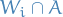 open in
open in  . So we let
. So we let

so there exists finite  with
with

Every space with cofinite topology is compact.
Let  . Take some
. Take some 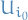 so that
so that 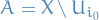 is finite.
is finite.
Then  , there exists
, there exists 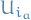 in cover with
in cover with  . Therefore
. Therefore

is a finite cover.
Idea: take away one cover → left with finitely many points → we good.
Motivation
Let  . For which
. For which  must
must  be bounded?
be bounded?
 finite
finite- If
 of opens with
of opens with  bounded then
bounded then  is bounded.
is bounded. Any continuous
 is locally bounded
is locally bounded

with
 bounded, e.g.
bounded, e.g.
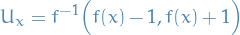
If there exists finitely many
 as above, with
as above, with
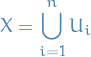
then
 is bounded.
is bounded.
Compactness NOT equivalent to:
 is a cover of
is a cover of 
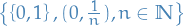 covers
covers ![$[0, 1]$](../../assets/latex/analysis_68c8fa38d960e53d4308cbf1e65d04c66a554817.png) but not finite.
but not finite.
 cover
cover ![$[0, 1]$](../../assets/latex/analysis_68c8fa38d960e53d4308cbf1e65d04c66a554817.png) → clearly not finite mate
→ clearly not finite mate
- Same as 2, but take finitely many

- Follows from 2 by taking subcover to be the whole cover.
 always covers
always covers  and has finite subcover (e.g.
and has finite subcover (e.g. 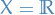 )
)
Examples
- Non-compact
 , so
, so  has no finite subcover, so
has no finite subcover, so  not compact
not compact- Infinite discrete space is not compact. Consider
 which is an open cover, but has no finite subcover.
which is an open cover, but has no finite subcover.
- Compact
 indiscrete so
indiscrete so  . Only open covers are
. Only open covers are  and
and  , and
, and  is a finite subcover, hence
is a finite subcover, hence  is compact.
is compact.- Any finite space is compact (for any topology)
Some specific spaces
Banach space
See Banach space
Hilbert space
A Hilbert space  is a vector space equipped by an inner product such that the norm induced by the inner product
is a vector space equipped by an inner product such that the norm induced by the inner product
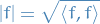
turns  into a complete metric space.
into a complete metric space.
A Hilbert space is thus an instance of a Banach space where we specifically define the metric as the square-root of the inner product.
Reproducing Kernel Hilbert Space
Here we only discuss the construction of Reproducing Kernel Hilbert Spaces on the reals, but the results can easily be extended to complex-valued too.
Let  be an arbitrary set and
be an arbitrary set and  a Hilbert space of real-valued functions on
a Hilbert space of real-valued functions on  . The evaluation functional over the Hilbert space of functions
. The evaluation functional over the Hilbert space of functions  is a linear functional that evaluates each function at a point
is a linear functional that evaluates each function at a point  ,
,

We say that  is reproducing kernel Hilbert space if, for all
is reproducing kernel Hilbert space if, for all  in
in  ,
,  is continuous at any
is continuous at any  in
in  , or, equiavelently, if
, or, equiavelently, if  is a bounded operator on
is a bounded operator on  , i.e. there exists some
, i.e. there exists some  such that
such that
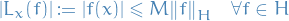
While this property for  ensure both the existence of an inner product and the evaluation of every function in
ensure both the existence of an inner product and the evaluation of every function in  at every point in the domain. It does not lend itself to easy application in practice.
at every point in the domain. It does not lend itself to easy application in practice.
A more intuitive definition of the RKHS can be obtained by observing that this property guarantees that the evaluation functional  can be represented by taking the inner product of
can be represented by taking the inner product of  with a function
with a function  in
in  . This function is the so-called reproducing kernel of the Hilbert space
. This function is the so-called reproducing kernel of the Hilbert space  from which the RKHS takes its name.
from which the RKHS takes its name.
The Riesz representation theorem implies that for all  there exists a unique element
there exists a unique element  of
of  with the reproducing property
with the reproducing property

Since  is itself a function in
is itself a function in  , it holds that for every
, it holds that for every  in
in  there exists a
there exists a  s.t.
s.t.
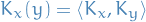
This allows us to define the reproducing kernel of  as a function
as a function  by
by

From this definition it is easy to see that  is both symmetric and positive definite, i.e.
is both symmetric and positive definite, i.e.
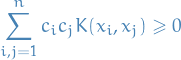
for any  ,
,  and some
and some  .
.
- RKHS in statistcal learning theory
The representer theorem states that every function in an RKHS that minimizes an empirical risk function can be written as a linear combination of the kernel function evaluated at the training points.
Let
 be a nonempty set and
be a nonempty set and  a postive-definite real-valued kernel on
a postive-definite real-valued kernel on  with corresponding RKHS
with corresponding RKHS  .
.
Given a training sample
 , a strictly monotonically increasing real-valued fuction
, a strictly monotonically increasing real-valued fuction  , and a arbitrary emipirical risk function
, and a arbitrary emipirical risk function  , then for any
, then for any  satisfying
satisfying
 admits a representation of the form
admits a representation of the form
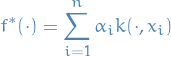
where
 for all
for all  and, as stated before,
and, as stated before,  is the kernel on the RKHS
is the kernel on the RKHS  .
.
Let
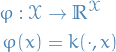
(so that
 is itself a map
is itself a map  )
)
Since
 is a reproducing kernel, then
is a reproducing kernel, then

where
 is the inner product on
is the inner product on  .
.
Given any
 , one can use the orthogonal projection to decompose any
, one can use the orthogonal projection to decompose any  into a sum of two functions, one lying in the
into a sum of two functions, one lying in the  and the other lying in the orthogonal complement:
and the other lying in the orthogonal complement:
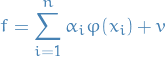
where
 for all
for all  .
.
The above orthogonal decomposition and the reproducing property of
 show that applying
show that applying  to any training point
to any training point  produces
produces
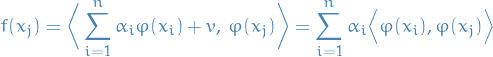
which we observe is independent of
 . Consequently, the value of the empirical risk
. Consequently, the value of the empirical risk  in defined in the representer theorem above is likewise independent of
in defined in the representer theorem above is likewise independent of  .
.
For the second term (the regularization term), since
 is orthogonal to summand-term and
is orthogonal to summand-term and 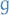 is strictly monotonic, we have
is strictly monotonic, we have
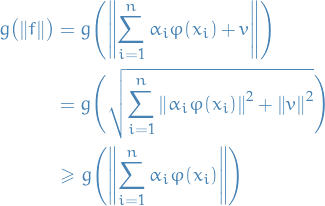
Therefore setting
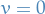 does not affect the first term of the empirical risk minimization, while it strictly decreasing the second term.
does not affect the first term of the empirical risk minimization, while it strictly decreasing the second term.
Consequently, any minimizer
 of the empirical risk must have
of the empirical risk must have 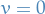 , i.e., it must be of the form
, i.e., it must be of the form
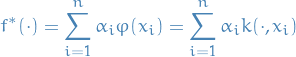
which is the desired result.
This dramatically simplifies the regularized empirical risk minimization problem. Usually the search domain
 for the minimization function will be an infinte-dimensional subspace of
for the minimization function will be an infinte-dimensional subspace of  (square-integrable functions).
(square-integrable functions).
But, by the representer theorem, we know that the representation of
 reduces the original (infinite-dimensional) minimization problem to a search for the optimal n-dimensional vector of coefficients
reduces the original (infinite-dimensional) minimization problem to a search for the optimal n-dimensional vector of coefficients  for the kernel for each data-point.
for the kernel for each data-point.
Theorems
Let  , then
, then
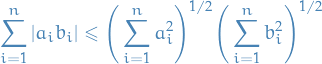
Let  . Consider the following polynomial
. Consider the following polynomial
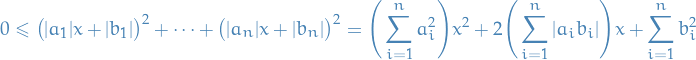
where we've used the fact that  for
for 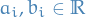 .
.
Since it's nonnegative, it has at most one real root for  , hence its discrimant is less than or equal to zero. That is,
, hence its discrimant is less than or equal to zero. That is,

Hence,
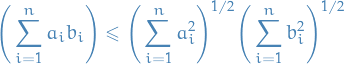
as claimed.
Let  be a metric space.
be a metric space.
- A sequence in
 can have at most one limit.
can have at most one limit. - If
 converges to
converges to  and
and  is any subsequence of
is any subsequence of  , then
, then  converges to
converges to  as
as 
- Every convergence sequence in
 is bounded
is bounded - Every convergence sequence in
 is Cauchy
is Cauchy
Let  . Then
. Then  as
as  if and only if
if and only if

Let  . Then
. Then  is closed if and only if the limit of every convergent sequence
is closed if and only if the limit of every convergent sequence  satisfies
satisfies

A set is open iff it equals its interior ; a set is closed iff it equals its closure .
Let 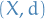 be a metric space and let
be a metric space and let  . Then,
. Then,  is dense if and only if
is dense if and only if 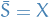 .
.
Any compact set must be closed and bounded.
The converse is not necessarily true (Heine-Borel Theorem addresses when this is true).
Bounded:
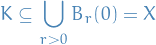
 is compact implies that
is compact implies that  s.t.
s.t.
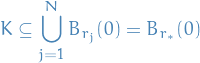
where
 .
.
Let 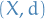 be a separable metric space which satisfies the Bolzano-Weierstrass Property and
be a separable metric space which satisfies the Bolzano-Weierstrass Property and  . Then
. Then  is compact if and only if it is closed and bounded.
is compact if and only if it is closed and bounded.
Observe that

is closed and bounded.
 is compact if and only if
is compact if and only if 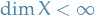 .
.
Suppose 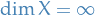 . Idea is cto construct
. Idea is cto construct  of unit vectors s.t.
of unit vectors s.t.

Example: continuous functions
![$\big( C([0, 1]), \norm{\cdot}_{L^\infty} \big)$](../../assets/latex/analysis_f10d5d78c04b9ac1817e46272c1ff549f3bac865.png) is a Banach space.
is a Banach space.
What are the compact sets ![$K \subseteq C([0, 1])$](../../assets/latex/analysis_2e16dc359c627731048e8518b88cef2cb0f48f17.png) ?:
?:
 is compact if and only if
is compact if and only if  is closed, bounded AND "something something" (what is it?)
is closed, bounded AND "something something" (what is it?)
Continuity and limits of functions
Let  where
where 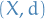 and
and 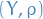 are metric spaces.
are metric spaces.
Then  if and only if for every
if and only if for every  we have
we have
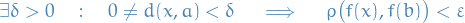
Or equivalently, if  is continuous on
is continuous on  ,
,

Connected sets
Let  be a metric space.
be a metric space.
- A pair of nonempty open sets
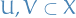 is said to separate
is said to separate  if and only if
if and only if  and
and 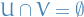
 is said to be connected if and only if
is said to be connected if and only if  cannot be separated by any pair of open sets
cannot be separated by any pair of open sets 
Loosely speaking, a connected space cannot be broken into smaller, nonempty, open pieces which do not share any common points.
Let  be a metric space, and
be a metric space, and 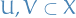 .
.
 are said to separate
are said to separate  if and only if:
if and only if:
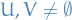 (non-empty)
(non-empty)
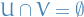
 is connected if and only if it cannot be separated by any
is connected if and only if it cannot be separated by any  .
.
A subset  is connected if and only if
is connected if and only if  is an interval
is an interval
A subset  of a metric space
of a metric space  is path-connected if for every
is path-connected if for every  there is a continuous function (path)
there is a continuous function (path) ![$\phi: [0, 1] \to E$](../../assets/latex/analysis_6184738782cb70109b33fdf41748761949272ac4.png) such that
such that

Let  be a metric space, and
be a metric space, and  .
.
If  is path-connected , then
is path-connected , then  is connected.
is connected.
Stone-Weierstrass Theorem
Notation
 is a metric space
is a metric space denotes a algebra in
denotes a algebra in 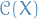


Goal
The goal of this section is to answer the following question:
Can one use polynomials to approximate continuous functions on an interval ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) ?
?
Stuff
Let  be a metric space.
be a metric space.
A set  is a said to be a (real function) algebra in
is a said to be a (real function) algebra in 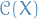 if and only if
if and only if

- If
 , then
, then  and
and  both belong to
both belong to 
- If
 and
and  , then
, then 
A subset  of
of 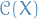 is said to be (uniformly) closed if and only if for each sequence
is said to be (uniformly) closed if and only if for each sequence  that satisfies
that satisfies  as
as  , the limit function
, the limit function  belongs to
belongs to  .
.
A subset  of
of 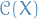 is said to be uniformly dense in
is said to be uniformly dense in 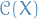 if and only if given
if and only if given  and
and  there is a function
there is a function  such that
such that  .
.
A subset  of
of 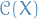 separates points of
separates points of  if and only if given
if and only if given  with
with 

Stone-Weierstrass Theorem
Suppose that  is a compact metric space.
is a compact metric space.
If  is an algebra in
is an algebra in 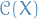 that separates points of
that separates points of  and contains the constant functions, then
and contains the constant functions, then  is uniformly dense in
is uniformly dense in 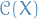 .
.
This is HUGE. It basically says that on any compact metric space, we can approximate any continuous function arbitrarily well using only the constants functions and some functions which separates points in the metric space!
You know what space satisfies this? Space of all polynomials!
Q & A
DONE Alternative definition of compact; consequences?
What's the difference between the definition of compactness and the following:
A set  is compact if for every subset
is compact if for every subset  there exists a finite covering
there exists a finite covering  .
.
Is there any difference; and if so, what are the consequences?
Answer
Yes, there is a difference.
In our new definition we're only saying that the EXISTS some finite covering, while the proper definition is sort of saying that all coverings of  does in fact contain a finite covering, a sort of "the lowest common denominator covering has to be finite, and each of these coverings do in fact have this".
does in fact contain a finite covering, a sort of "the lowest common denominator covering has to be finite, and each of these coverings do in fact have this".
Fixed Point Theory
Differential Equations
Notation
Stuff
In this section we're considering the large class of ODEs of the form
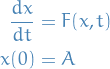
there will exists a unique solution  for
for  sufficiently small.
sufficiently small.
To ensure the existence of a unique solution, we need to consider the following:
Suppose  and
and  . Also suppose
. Also suppose  and
and  and
and
![\begin{equation*}
F: [A - \rho, A + \rho] \times [-r, r] \to \mathbb{R}
\end{equation*}](../../assets/latex/analysis_c9ddc35a4b00aa728286a03ed85db37856e4c4a5.png)
is continuous.
Further, suppose that for all ![$x, y \in [A - \rho, A + \rho]$](../../assets/latex/analysis_175d5c1c72ff749ff44e2ce3e0131678303ec09c.png) and
and ![$t \in [-r, r]$](../../assets/latex/analysis_3adcafac40b791f1895983b733f8e2180cc1de2e.png) there exists
there exists  such that
such that

Due to Mean Value Theorem, if  exists and is continuous on
exists and is continuous on ![$[A - \rho, A + \rho] \times [-r, r]$](../../assets/latex/analysis_65edd9aed40242497d2e71bf8dc765b9fc2019fe.png) then the above is satisfied.
then the above is satisfied.
Suppose  satisfies a Lipschitz condition as above. Then there exists an
satisfies a Lipschitz condition as above. Then there exists an  such that the ODE
such that the ODE
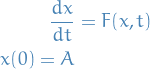
has a unique solution  for
for  .
.
Exercises
From the notes
A contraction is continuous
A contraction  is continuous.
is continuous.
Let  , and let
, and let  be a contraction. Now, for the sake of contradiction, suppose
be a contraction. Now, for the sake of contradiction, suppose  is discontinuous at some point
is discontinuous at some point  .
.
Due to  being a contraction, then for any two points
being a contraction, then for any two points  we have
we have

where  . Since
. Since  is arbitrary we can let
is arbitrary we can let  be such that
be such that

Clearly,

Thus,
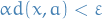
Which implies,

But this is only true if and only if  is continuous; hence we have our contradiction.
is continuous; hence we have our contradiction.
TODO Exercise 1
Suppose  is a contraction mapping.
is a contraction mapping.
If
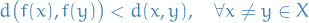
then any fixed point will be unique, whether or not  is complete.
is complete.
Further, show that if  is not complete, then a fixed-point does not necessarily exist.
is not complete, then a fixed-point does not necessarily exist.
Let  be a metric space.
be a metric space.
For the first part of our claim, suppose the mapping  satisfies
satisfies

Then clearly  is a contraction, since we can always choose
is a contraction, since we can always choose  such that
such that

due to the interval  being dense in
being dense in ![$[0, 1]$](../../assets/latex/analysis_68c8fa38d960e53d4308cbf1e65d04c66a554817.png) .
.
Now, for the sake of contradiction suppose there exists two different fixed-points,  . Then, from the property above of
. Then, from the property above of  , we have
, we have
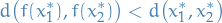
But, since  and
and  are fixed-points, we have
are fixed-points, we have

Hence, the above inequality implies

Which clearly is a contraction, hence if there exists a fixed-point of  , then that is a unique fixed-point.
, then that is a unique fixed-point.
Now, for the second part of the claim,
PROBABLY EXIST SOME COUNTER-EXAMPLE THAT I CAN'T THINK OF. SOME  SUCH THAT THIS IS NOT THE CASE.
SUCH THAT THIS IS NOT THE CASE.
TODO Exercise 2
Let  be a metric space which is not complete. Then there exists contractions with no fixed point.
be a metric space which is not complete. Then there exists contractions with no fixed point.
Probably some counter-example I can't think of.
TODO Exercise 3
Note taken on
Regarding the previous note, could we not have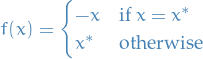
which for even
 we would still have
we would still have  be a contraction mapping, but for odd
be a contraction mapping, but for odd  it would not be! Therefore I believe it's reasonable to assume that they mean for any
it would not be! Therefore I believe it's reasonable to assume that they mean for any  .
.
- Note taken on
But alone does not imply that
alone does not imply that  since
since  , could be
, could be  , hence there needs to be something else which ensures this implication. That is, if the claim is supposed to be true for any
, hence there needs to be something else which ensures this implication. That is, if the claim is supposed to be true for any  , then yeah, this implication would definitively hold, but I'm not sure that is what they mean
, then yeah, this implication would definitively hold, but I'm not sure that is what they mean - Note taken on
 being a contraction in a complete metric space =>
being a contraction in a complete metric space =>  is a contraction in a complete metric space =>
is a contraction in a complete metric space =>  has a unique fixed point in this space: NOPE! We can have fixed points without the function
has a unique fixed point in this space: NOPE! We can have fixed points without the function  being a contraction, also
being a contraction, also  being a contraction does not in fact imply that
being a contraction does not in fact imply that  is a contraction! See Exercise 4 for a counter-example.
is a contraction! See Exercise 4 for a counter-example.
Let  be a complete metric space, and suppose
be a complete metric space, and suppose  is such that
is such that

is a contraction. Then  has a unique fixed point.
has a unique fixed point.
As proven in the first part of Exercise 1 we know that any contraction  has a unique fixed point when
has a unique fixed point when  is a complete metric space. Thus, we know that there exists some
is a complete metric space. Thus, we know that there exists some  such that
such that

If we assume the claim is supposed to hold for any  , and not a specific arbitrary
, and not a specific arbitrary  , then the above implies
, then the above implies

Further, if  was not unique, then
was not unique, then

for some  , but this implies that
, but this implies that  has another fixed point, which we know cannot be.
has another fixed point, which we know cannot be.
Hence, if  is a contraction, then
is a contraction, then  has a unique fixed point.
has a unique fixed point.
TODO Exercise 4
Note taken on
Maaaybe you can build some argument by creating two linear functions and
and 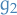 which intersect
which intersect  at a single point
at a single point 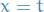 , and such that
, and such that
![\begin{equation*}
g_1(t) = g_2(t) = \cos t, \quad g_1(x) \le \cos x, \quad g_2(x) \ge \cos x, \quad x \in [0, t]
\end{equation*}](../../assets/latex/analysis_8bd7d58244fdab167992a15c695ddb8a35aa2571.png)
Basically, consider two functions for which we can easily compute the effect of
 for two points
for two points  and
and  on the distance between them
on the distance between them  which we can clearly tell has the property that
which we can clearly tell has the property that  , buuut I'm not going to bother spending time on this now.
, buuut I'm not going to bother spending time on this now.
Note taken on
But, if we can show that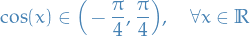
and then

we're good!
Note taken on
I was wondering if we can use some function on the interval
on the interval  which is defined such that
which is defined such that

which also has the property that
 for
for  , and then we potentially compute the distance of the difference between these functions to obtain some upper-bound on
, and then we potentially compute the distance of the difference between these functions to obtain some upper-bound on  which related to
which related to  .
.

Doesn't seem to work very well though
- Note taken on
Technically we only need to prove that is a contraction mapping on the open interval
is a contraction mapping on the open interval  , since for
, since for  not in this interval,
not in this interval,  will lie in the interval specified before.
will lie in the interval specified before.
 is not a contraction, but
is not a contraction, but  is a contraction.
is a contraction.
Further, this implies that there is a unique solution in  to the equation
to the equation

Clearly  is not a contraction, since
is not a contraction, since
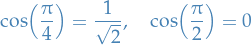
which implies

and
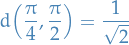
Hence,
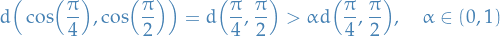
NOW PROVE THAT  IS A CONTRACTION MAPPING YAH FOOL
IS A CONTRACTION MAPPING YAH FOOL
Fourier Series
Notation
Definition
Let  be integrable on
be integrable on ![$[- \pi, \pi]$](../../assets/latex/analysis_8ccfa4861271a40956d9a5fddb99884ce26ce0c6.png) .
.
The Fourier coefficients of  are numbers
are numbers

and

Let  be integrable on
be integrable on ![$[- \pi, \pi]$](../../assets/latex/analysis_8ccfa4861271a40956d9a5fddb99884ce26ce0c6.png) and let
and let  be a nonnegative integer.
be a nonnegative integer.
We define the Fourier series of  as the trigonometric series
as the trigonometric series

and the partial sum of  of order
of order  to be the trigonometric polynomial defined
to be the trigonometric polynomial defined

Kernels
Dirichlet kernel
Let  be nonnegative integer.
be nonnegative integer.
The Dirichlet kernel of order  is the function defined
is the function defined
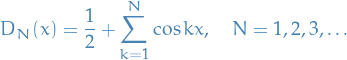
with the special case of 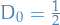 .
.
It turns out it can also be written as
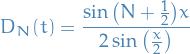
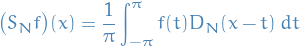
for all ![$x \in [-\pi, \pi]$](../../assets/latex/analysis_b6623df41ea8c5cec3380cab5139b04d7c35813a.png) and
and  .
.
That is, we can write the N-th order Fourier partial sum as a convolution between  and the Dirichlet kernel.
and the Dirichlet kernel.
![\begin{equation*}
\begin{split}
\big( S_N f \big) (x) &= \frac{1}{2 \pi} \int_{-\pi}^{\pi} f(t) \ dt + \frac{1}{\pi} \sum_{k=1}^{N} \int_{-\pi}^{\pi} f(t) \Big( \cos kt \cos kx + \sin kt \sin kx \Big) \ dt \\
&= \frac{1}{\pi} \Bigg[ \int_{-\pi}^{\pi} \Bigg( \frac{1}{2} + \sum_{k=1}^{N} \cos \Big( k (x - t) \Big) \Bigg) f(t) \ dt \Bigg]
\end{split}
\end{equation*}](../../assets/latex/analysis_0e6754c427298fb24ff98648707806eab0cc0fc3.png)
where we've brought the intergrals together and used the trigonometric identity

Finally remembering that
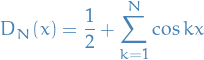
We see that the above expression is simply
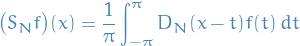
as claimed.
Suppose that ![$f_N: [-\pi, \pi] \to \mathbb{R}$](../../assets/latex/analysis_9bb56fef7a0123394a78936fbe764d04b2c81711.png) is integrable and that
is integrable and that 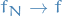 uniformly on
uniformly on ![$[- \pi, \pi]$](../../assets/latex/analysis_8ccfa4861271a40956d9a5fddb99884ce26ce0c6.png) . Then,
. Then,

as  uniformly in
uniformly in  .
.
We know that  such that
such that
![\begin{equation*}
\forall N \ge N_0 \quad \implies \quad |f_N - f| < \varepsilon, \quad \forall x \in [-\pi, \pi]
\end{equation*}](../../assets/latex/analysis_e2183e22e7f2ea8b02cf5266ede72113418c7763.png)
Then we have,
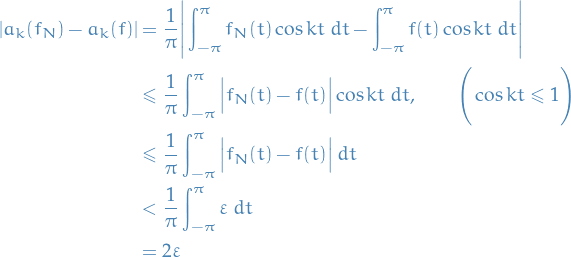
I.e. we can make the difference between the coefficients as small as we'd like, hence

The very same argument holds for  .
.
Fejér kernel
The Fejér kernel of order  is the function defined
is the function defined
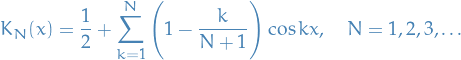
with the special case of 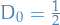 .
.
Functional Analysis
Notation
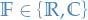 is the fields we'll be using
is the fields we'll be using
"Small Lp" space:
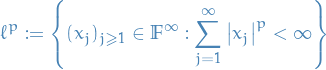
Let
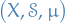 be a measure space and
be a measure space and  , then
, then

denotes the set of all measurable functions
 on
on  such that
such that  and the values of
and the values of  are real numbers, except possibly on a set of measure
are real numbers, except possibly on a set of measure  .
.
Lp space:
![\begin{equation*}
L^p = \left\{ f: [0, 1] \to \mathbb{R} : \norm{f}_{L^p} < \infty \right\}
\end{equation*}](../../assets/latex/analysis_07d28570438667e9ce005288e62357a7bbad4cde.png)
where
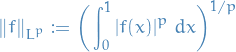
Or more accurately,

where
 denotes the equivalence classes of the equivalence relation
denotes the equivalence classes of the equivalence relation

- NLS means normed linear spaces
Theorems
Inequalities
Let 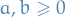 such that
such that  . Then
. Then
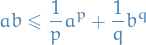
For any two sequences  and
and  of nonnegative numbers, we have
of nonnegative numbers, we have
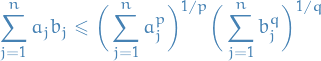
for any  where
where  is the conjugate exponent of
is the conjugate exponent of 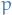 , i.e.
, i.e.

Observe that this aslo includes 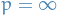 and
and  !
!
For 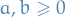 and
and  :
:
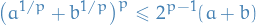
From Hölders inequality we have
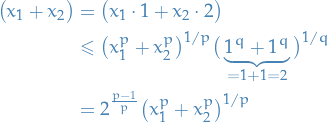
where  . Finally, letting
. Finally, letting 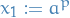 and
and 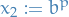 , we get
, we get
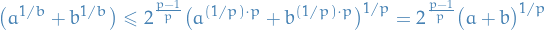
And taking both sides to the power of 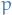 :
:
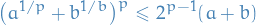
as wanted.
For any two elements 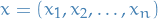 and
and 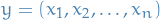 of
of  , we have
, we have
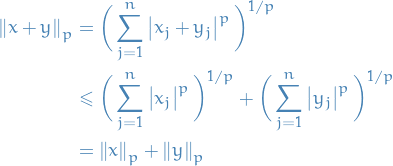
for any  .
.
Mercer's theorem
Let ![$K: [a, b]^2 \to \mathbb{R}$](../../assets/latex/analysis_9094fa2e92b0f7404e1360129684d05a5019f3c5.png) be a symmetric continuous function, often called a kernel.
be a symmetric continuous function, often called a kernel.
 is said to be non-negative definite (or positive semi-definite) if and only if
is said to be non-negative definite (or positive semi-definite) if and only if
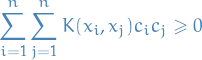
for all fininte sequences of points ![$x_1, \dots, x_n \in [a, b]$](../../assets/latex/analysis_df408ebd5b590a92452fc6df4e55a0f880cc7ffc.png) and all choices of real numbers
and all choices of real numbers  .
.
We associate with  a linear operator
a linear operator ![$T_K: L^2([a, b]) \to L^2([a, b])$](../../assets/latex/analysis_5f9dfc4f9e9bcce9ac9d7c164cb268f6a8bc8c39.png) by
by
![\begin{equation*}
\big( T_K \varphi \big) (x) = \int_{a}^{b} K(x, s) \varphi(s) \ ds, \quad \varphi \in L^2([a, b])
\end{equation*}](../../assets/latex/analysis_e0221b304336728d74b7277973b37066aeef26fc.png)
The theorem then states that there is an orthonormal basis  of
of ![$L^2([a, b])$](../../assets/latex/analysis_46dd0ac7af731cb49a65fdba69a9f752782dd5f8.png) consisting for eigenfunctions of
consisting for eigenfunctions of  such that the corresponding sequence of eigenvalues
such that the corresponding sequence of eigenvalues  is nonnegative.
is nonnegative.
The eigenfunctions corresponding to non-zero eigenvalues are continuous on ![$[a, b]$](../../assets/latex/analysis_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) and
and  has the representation
has the representation

where the convergence is absolute and uniform.
There are also more general versions of Mercer's thm which establishes the same result for measurable kernels, i.e.  on any compact Hausdorff space
on any compact Hausdorff space  .
.
Banach spaces
A norm on a vector space  over
over  (
(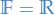 or
or  ) is a map
) is a map
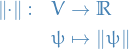
with the following properties:
- For all
 ,
,  , with equality if and only if
, with equality if and only if 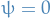
- For all
 and
and  , we have
, we have 
For all
 , we have
, we have

If  is a norm on
is a norm on  , then we can define a metric
, then we can define a metric  on
on  by setting
by setting  .
.
A normed vector space is said to be a Banach space if it is complete wrt. the associated metric.
A Banach space is said to be separable if it contains a countable dense subset.
Let  be a normed space and
be a normed space and  a Banach space.
a Banach space.
Suppose 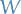 is a dense subset of
is a dense subset of  and that
and that  is a bounded linear operator.
is a bounded linear operator.
Then there exists a unique bounded linear map  such that
such that

where  denotes the restriction of
denotes the restriction of  to the subspace
to the subspace  .
.
Furthermore, the norm of  equals the norm of
equals the norm of  .
.
Suppose that  is a Banach space and
is a Banach space and  a normed vector space.
a normed vector space.
For any linear map 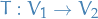 , let
, let  denote the set of pairs
denote the set of pairs  in
in  such that
such that  .
.
If the graph of  is a closed subset of
is a closed subset of  , then
, then  is bounded.
is bounded.
Examples
Equip ![$C \big( [0, 1] \big)$](../../assets/latex/analysis_8a6793132a8063104c20b7b52560ffd95a9ff44f.png) with the norm
with the norm
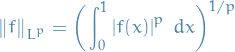
Then,
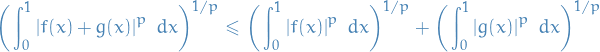
Metric space structure on NLS
Let 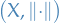 is a NLS of
is a NLS of  is a subspace.
is a subspace.
If  is open, then
is open, then 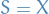 .
.
Clearly  , hence
, hence  there exists
there exists
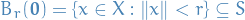
Observe that  if and only if
if and only if  for some
for some  .
.  by definition of a subspace, and reverse is
by definition of a subspace, and reverse is  which implies that
which implies that  .
.
Cosnider  since
since  . Then,
. Then,
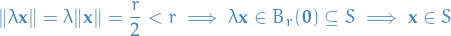
So basically, since a linear space is closed under scalar multiplication, any open subspace  must contain any scaling of
must contain any scaling of  , hence it must contain the entire space.
, hence it must contain the entire space.
Let  be a NLS with
be a NLS with 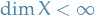 .
.
Then  is closed.
is closed.
Completion of NLS
Notation
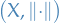 denotes a NLS which is not necessarily complete
denotes a NLS which is not necessarily complete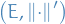 denotes the completion of
denotes the completion of 
Set of Cauchy sequences in
 :
:
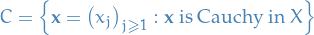
Stuff
- Formal procedure to "fill holes" in an NLS, i.e. making non-complete NLS (NLS for which Cauchy sequences does not necessarily converge), well, complete!
- Observe that
 is dense in the completion of
is dense in the completion of  , i.e.
, i.e. 
- Let
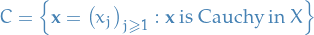 .
.
Let
 on
on  be the equivalence relation such that
be the equivalence relation such that

Let  be a Banach space, and let
be a Banach space, and let  be a subspace.
be a subspace.
Then  is a Banach space if and only if
is a Banach space if and only if  is closed.
is closed.
 Suppose
Suppose  is closed. Let
is closed. Let  be Cauchy. Then
be Cauchy. Then  is Cauchy in
is Cauchy in  .
And since
.
And since  is closed,
is closed,  contains all its limit points, hence all convergent sequences in
contains all its limit points, hence all convergent sequences in  converges to a point in
converges to a point in  , i.e.
, i.e.  is Banach.
is Banach.
 . Suppose
. Suppose  is a Banach space.
Let
is a Banach space.
Let  s.t.
s.t.  for some
for some  .
Note that
.
Note that  is Cauchy, and since
is Cauchy, and since  is Banach, there exists an
is Banach, there exists an  s.t.
s.t.  as
as  . Then
. Then

Hence,  , and
, and  is closed.
is closed.
Let  and
and  be two normal linear spaces.
be two normal linear spaces.
- A linear map
 is said to be an isometry if
is said to be an isometry if 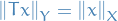 for all
for all  .
. - We say
 and
and  are isometrically isomorphic if there exists an isometry
are isometrically isomorphic if there exists an isometry  from
from  to
to  .
.
- Note that
 is automatically a surjective isometry.
is automatically a surjective isometry.
- Note that
- The Banach space completion of
 is a pair, consisting of a Banach space
is a pair, consisting of a Banach space  and an isometry
and an isometry  s.t.
s.t.  is a dense subspace of
is a dense subspace of  .
.
Let 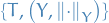 and
and 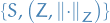 be two completions of
be two completions of  .
.
Then  and
and  are isometrically isomorphic.
are isometrically isomorphic.
Let  be an NLS.
be an NLS.
Then there exists a unique a Banach space completion of  .
.
Let
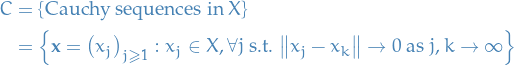
Equivalence relation
 on
on 

Let
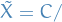 , and define
, and define
![\begin{equation*}
\begin{split}
T: \quad & X \to \tilde{X} \\
& x \mapsto Tx = [\mathbf{x}]
\end{split}
\end{equation*}](../../assets/latex/analysis_a8126eee401a3f468abb9bf8297f2188f0603fdd.png)
Observe that
![\begin{equation*}
\mathbf{y} \in [\mathbf{x}] \iff \norm{y_j - x} \to 0
\end{equation*}](../../assets/latex/analysis_ec1a86a40c65eac83c10217f78c6202c0a211e9e.png)
i.e. all sequences which converges to
 .
.
Equip
 a vector space structure, i.e. addition
a vector space structure, i.e. addition
![\begin{equation*}
[\mathbf{x}] + [ \mathbf{y}] = [\mathbf{z}], \quad \mathbf{z} = \big( x_j + y_j \big)_{j \ge 1} \in C
\end{equation*}](../../assets/latex/analysis_a501bd7d7765d7b68308d5a782b2aa6aa7fb5140.png)
and scalar multiplication
![\begin{equation*}
\lambda [\mathbf{x}] = [\lambda \mathbf{x}]
\end{equation*}](../../assets/latex/analysis_568bc53761573745d90260e1166e155ce83cb382.png)
Equip
 with a norm
with a norm 
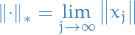
Observe that

By completion of the underlying field
 ,
,  is Cauchy and thus converges. Hence the above norm is defined
is Cauchy and thus converges. Hence the above norm is defined
Need to check that this is well-defined:
![\begin{equation*}
y \in [\mathbf{x}] \iff \norm{y_j - x_j} \to 0 \iff \lim_{j \to \infty} \norm{y_j} = \lim_{j \to \infty} \norm{x_j}
\end{equation*}](../../assets/latex/analysis_56e45eaa2511a52884243f13f496b6056c05c22e.png)
 is a Banach space
is a Banach spaceThen
 is a linear map, then
is a linear map, then
![\begin{equation*}
\norm{T \mathbf{x}}_{*} = \norm{[\mathbf{x}]}_{*} = \lim_{j\to \infty} \norm{x_j} = \norm{x}
\end{equation*}](../../assets/latex/analysis_9e9812f841499e9885f9ae2068f73891d2ce5f09.png)
Finally, one can show that
 is dense in
is dense in  , hence we have our Banach space completion.
, hence we have our Banach space completion.
Example
Let  be a subspace.
be a subspace.
 , i.e.
, i.e.  is closed in
is closed in  .
.
Let  , thus
, thus  . Then
. Then

for some  .
.
We then need to show that  or
or  as
as  . or
. or

Given  . Then
. Then  s.t.
s.t.  .
But
.
But  implies
implies

So for  ,
,

So basically, show that a sequence of sequences  converge to some sequence
converge to some sequence  , thus
, thus  contains all it's limit points, hence
contains all it's limit points, hence  is closed.
is closed.
Consider the NLS ![$\big( C([0, 1]), \norm{\cdot}_{L^p} \big)$](../../assets/latex/analysis_0beb12faa8264445971d8af40206cf4e849a84ad.png) for
for  .
.
Let
![\begin{equation*}
S = \left\{ f \in C([0, 1]) : f(0) = 0 \right\}
\end{equation*}](../../assets/latex/analysis_a058cbfca87a98d53838bdd80011bcdcc53f6576.png)
Then  is not closed, but
is not closed, but  is dense in
is dense in ![$C([0, 1])$](../../assets/latex/analysis_d0a786318a6f7e61dfb7af9b501295ff0c1a81b9.png) , i.e.
, i.e.
![\begin{equation*}
\overline{S} = C([0, 1])
\end{equation*}](../../assets/latex/analysis_1e17bfffa65218879509d202ecbf5f47d6153b12.png)
Let
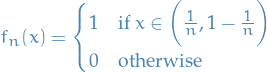
Then  , therefore
, therefore  .
But
.
But 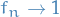 , but
, but 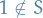 , hence
, hence  does not contain all of its limit points, i.e. is not closed, proving our first claim.
does not contain all of its limit points, i.e. is not closed, proving our first claim.
Now suppose that ![$f \in C([0, 1])$](../../assets/latex/analysis_795511f38a674f2eca972b1e89f37e957086b05e.png) . We now want to show that
. We now want to show that  such that
such that  and
and  .
.
TO THIS.
Equivalence of norms
- We'll be referring to norms as equivalent if the induced norms are strongly equivalent metrics
Two norms  and
and  on
on  are said to be equivalent if there is a constant
are said to be equivalent if there is a constant  s.t.
s.t.

This does in fact define an equivalence relation on norms.
Hilbert spaces
Let  be a
be a  and
and  its dual space.
Then the map
its dual space.
Then the map

Then  is isometric isomorphism.
is isometric isomorphism.
If  is a bounded linear functional, then there exists a unique
is a bounded linear functional, then there exists a unique  such that
such that

Furthermore, the operator norm of  as a linear functional is equal to the norm of
as a linear functional is equal to the norm of  as an element of
as an element of  .
.
 and
and  s.t.
s.t. 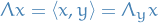
Assume
 and consider
and consider

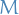 is closed (
is closed ( cont.) and subspace (
cont.) and subspace ( linear) of
linear) of  . Then
. Then

since
 .
.
- But
 implies there exists nonzero
implies there exists nonzero  .
. Take

and check
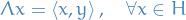
Basis in Hilbert spaces
Orthogonal decomposition
If  , then
, then

For any seminorm  defined by a semi-inner product and any
defined by a semi-inner product and any  ,
,
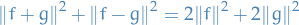
For any inner product space 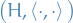 , and any Hilbert subspace
, and any Hilbert subspace  , and
, and  there is a unique representation
there is a unique representation
with  and
and  .
.
Idea:
- Prove existence of orthogonal decomposition
- Proof by contradiction
- Consider a lower-bound on the distance between
 for
for  , and then show that this is violated if
, and then show that this is violated if  , i.e. the "rest" of
, i.e. the "rest" of  is not in
is not in  .
.
- Prove uniqueness
Let

Then let  such that
such that  and
and  .
.
Then, by lemma:parallelogram-law we have

thus,
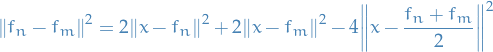
By completeness of  , we know that
, we know that  . Further, observe that
. Further, observe that  , thus by def. of
, thus by def. of  ,
,
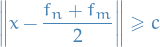
Thus, as  , we have
, we have 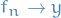 for some
for some  .
.
Now let 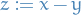 . Then
. Then

by continuity of  and the fact that
and the fact that  and
and 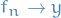 .
.
Further, suppose that  for some
for some  . Let
. Let
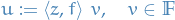
and  .
.
Then we observe that
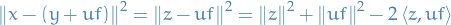
Substituting back in our epxression for  :
:
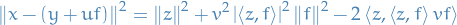
The last term is simply  , thus
, thus

For sufficiently small  , the
, the  term dominates which implies that
term dominates which implies that

for  .
.
This clearly contradicts our definition of  , hence we have the proof of decomposition existence by contradiction.
, hence we have the proof of decomposition existence by contradiction.
For uniqueness of the decomposition, we simply observe that if also  for some
for some  and
and  , then
, then

thus

which implies 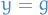 and
and 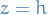 .
.
Many functions in 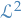 of Lebesgue measure, being unbounded, cannot be integrated with the classical Riemann integral. Therefore spaces of Riemann integrable functions would not be complete in the
of Lebesgue measure, being unbounded, cannot be integrated with the classical Riemann integral. Therefore spaces of Riemann integrable functions would not be complete in the 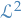 norm, and the orthogonal decomposition would not apply to them.
norm, and the orthogonal decomposition would not apply to them.
Another victory for good ole' Lebesgue!
Orthonormal sets and bases
A set  in a semi-inner product space
in a semi-inner product space  is called orthonormal if and only if
is called orthonormal if and only if

For any orthonormal set  and
and  ,
,

If 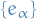 is an orthonormal set in
is an orthonormal set in  , and
, and  , where
, where
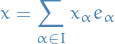
and

Then 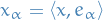 and
and  for all
for all  .
.
Furthermore,

For any Hilbert space  , any orthonormal set
, any orthonormal set 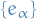 and any
and any  , then
, then

 : Follows from Bessel's inequality and Parseval-Bessel equality, since we have
: Follows from Bessel's inequality and Parseval-Bessel equality, since we have
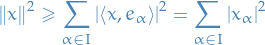
where the first equality is from Bessel's inequality and the second from Parseval-Bessel equality.
 : For each
: For each  choose a finite set
choose a finite set  such that
such that  increases with
increases with  and
and
Then
is a Cauchy sequence, hence converges to some  since
since  is complete.
is complete.
Then the net of all partial sums converges to the same limit, concluding our proof.
Let  be any inner product space and
be any inner product space and  be any linearly independent sequenec in
be any linearly independent sequenec in  .
.
Then there is an orthonormal sequence  in
in  s.t. for each
s.t. for each  ,
,  and
and  have the same linear span.
have the same linear span.
- Side-note on why Hilbert space > Banach space when talking about bases
In any vector space
 , a Hamel basis is a set
, a Hamel basis is a set  such that every
such that every  can be written uniquely as
can be written uniquely as

with only finitely many
 .
.
So, Hamel basis is an algebraic notion, which does not relate to any topology on
 .
.
In a separable Banach space
 , a Schauder basis is a sequence
, a Schauder basis is a sequence  such that for every
such that for every  ,
,
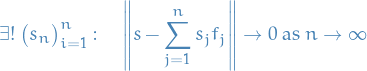
It is possible to find a Schauder basis in the "most useful" separable Banach spaces, but Schauder bases may not be conditional bases, and in general it may be very hard to find unconditional bases.
- Orthonormal basis for Hilbert space
Coming up with a basis for an infinite-dimensional space comes down to constructing a sequence of orthonormal vectors
 by taking some vector for which the projection
by taking some vector for which the projection  , i.e. all of
, i.e. all of  does not lie in
does not lie in 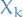 .
.
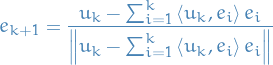
Then we prove that this gives us a space which is dense in the "parent" space.
More concretely, let
 and
and  be defined by choosing some
be defined by choosing some  such that
such that  , i.e.
, i.e.  , and
, and
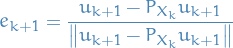
Every Hilbert space has an orthonormal basis.
If a collection of orthonormal sets is linearly ordered by inclusion (a chain), then their union is clearly an orthonormal set.
Thus by Zorn's lemma, let
 be the maximal orthonormal set.
be the maximal orthonormal set.
Take any
 . Let
. Let

where the sum converges by Bessel's inequality and Riesz-Ficher theorem.
If
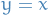 , we are done. Otherwise, then
, we are done. Otherwise, then  for all
for all  , so we can adjoin a new element
, so we can adjoin a new element
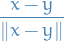
contradicting the maximality of the orthonormal set.
Every Hilbert space is isometric to a space
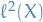 for some set
for some set  .
.
Let
 be an orthonormal basis for
be an orthonormal basis for  .
.
Then
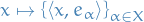 takes
takes  into
into 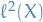 by Bessel's inequality.
by Bessel's inequality.
This function preserves inner products by the Parseval-Bessel equality. It is onto
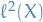 by the Riesz-Fischer theorem, concluding our proof.
by the Riesz-Fischer theorem, concluding our proof.
For any inner product space
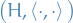 , an orthonormal set
, an orthonormal set  is an orthonormal basis of
is an orthonormal basis of  if and only if its linear span
if and only if its linear span  is dense in
is dense in  .
.
Let
 be a orthonormal sequence in a Hilbert space
be a orthonormal sequence in a Hilbert space  .
.
The following are equivalent:
If
 s.t.
s.t.  for all
for all  , then
, then
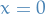
In other words, the sequence
 is a maximal orthonormal family of vectors.
is a maximal orthonormal family of vectors.
Span of
 is dense in
is dense in 

Unique convergence
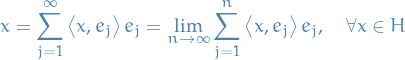
then
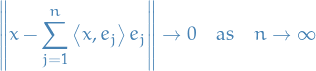
Inner product on basis
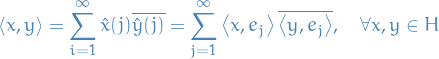
The norm
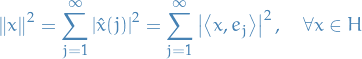
If one of these statements hold (and thus all of them hold), we say
 is an orthonormal basis of
is an orthonormal basis of  .
.
 : Idea is that
: Idea is that  implies
implies  as a subspace is simply
as a subspace is simply  , hence the closure is dense in
, hence the closure is dense in  .
.
Suppose
 .
.
Then since
 , we have
, we have  and so
and so  s.t.
s.t.  and
and  for all
for all  . But this is a contradiction wrt.
. But this is a contradiction wrt.  , hence we have our proof.
, hence we have our proof.
 : Let
: Let  and since
and since  .
.
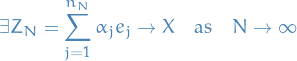
Set
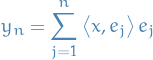
We make the following observations:
 and
and  .
. as
as  which tells us that a particular subsequence converges.
which tells us that a particular subsequence converges. we have
we have  ,
,
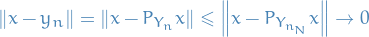
as
 , since
, since  . Which tells us that all possible subsequences converge.
. Which tells us that all possible subsequences converge.
Therefore
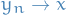 .
.
 :
:
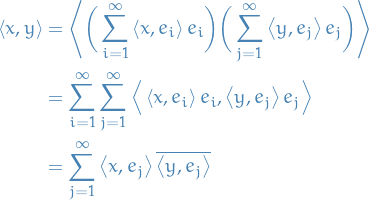
were we have used the interchanging of limits on multiple occasions, and in the final equality used the orthogonality of the
 .
.
 : Apply 4 with
: Apply 4 with 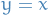 .
.
 : Otherwise we would have extra terms for the norm, rather than just the "Fourier" coefficients → contradiction.
: Otherwise we would have extra terms for the norm, rather than just the "Fourier" coefficients → contradiction.
Bounded Linear Operators
Notation
 be linear operator and
be linear operator and  and
and  are normed linear spaces
are normed linear spaces be vector space of bounded linear operators from
be vector space of bounded linear operators from  to
to  .
.- $T ∈
Stuff
Let  be linear operator and
be linear operator and  and
and  are normed linear spaces.
are normed linear spaces.
Then the following are equivalent
 is continuous on all of
is continuous on all of 
 is continuous at
is continuous at 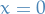
 is bounded
is bounded
 is seen by observing that for a sequence
is seen by observing that for a sequence  we have
we have

and so  and
and  are equivalent.
are equivalent.
 : Suppose
: Suppose  is continuous at
is continuous at 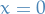 . Thus
. Thus 
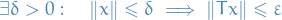
Let  , and let
, and let 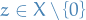 and
and

So

which gives us

If 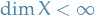 , then all linear maps
, then all linear maps  are continuous.
are continuous.
Hence  .
.
T is onto: let

Then 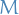 is a closed subspace of
is a closed subspace of  .
.
Suppose  , then we can decompose
, then we can decompose  , then this implies there exists some nonzero
, then this implies there exists some nonzero  .
.
Let  and consider
and consider

Then observe that

which implies that
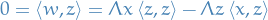
which implies
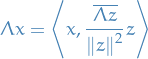
So for

Therefore,
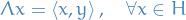
or equiv,
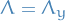
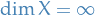 and
and 
Let

is the subspace of finite rank operators.
Then for  and
and  , there exists
, there exists  , i.e. constants which depend on
, i.e. constants which depend on  (functions yo!) s.t.
(functions yo!) s.t.

Then:
 is linear
is linear 
 are linear for all
are linear for all 
 bounded / cont.
bounded / cont. 
 are bounded / cont. for all
are bounded / cont. for all 
If  then
then 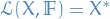 , i.e. the dual space of
, i.e. the dual space of  !
!
If  is a Banach space, then
is a Banach space, then  is a Banach space.
is a Banach space.
Examples with  , i.e.
, i.e. 
 for
for 
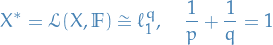
Fix  and define
and define
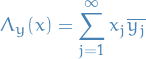
Then
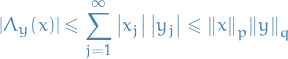
by Hölder's inequality. So 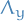 is bounded,
is bounded,

(remember we fixed 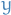 ).
).
Hence  and
and  .
.
Letting
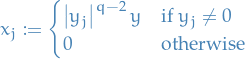
Then we attain the UB, and so we have equality.
We can then isometrically embed 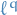 into
into  . That is, we can show that for any
. That is, we can show that for any  , there exists
, there exists  s.t.
s.t.
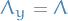
Hilbert-Schmidt operators
Let  where
where  are separable Hilbert spaces.
are separable Hilbert spaces.
We say that  is a Hilbert-Schmidt operator if
is a Hilbert-Schmidt operator if
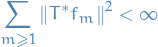
The space of all such operators are denoted  with the norm defined
with the norm defined

 is a vector space and
is a vector space and

but  is not a closed subspace of
is not a closed subspace of  since
since

- Suppose
 be a ONB for
be a ONB for  and
and  ONB for
ONB for  .
. Let
 then
then
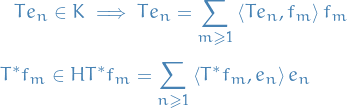
and
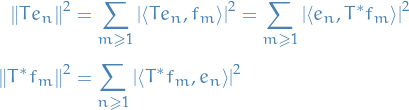
Thus,
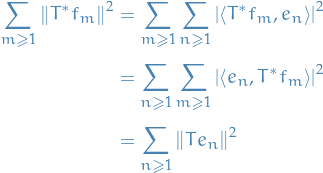
(switching sums we can always when all the terms are nonnegative).
- Hence, the definition of a Hilbert-Schmidt operator (also the norm
 ) is independent of the choice of ONB
) is independent of the choice of ONB
Let
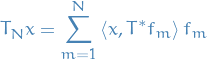
Then  is a FR operator.
is a FR operator.
 as
as  then
then

since then  which would imply that
which would imply that  contain the limit points of
contain the limit points of  .
.
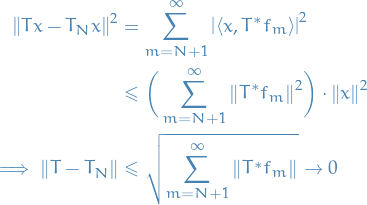
since  i.e.
i.e.
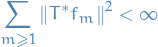
Example: kernel operators on ![$X = C([0, 1])$](../../assets/latex/analysis_8fe674cfb6c700fd8b70de8404a7c4713bc0d852.png)
Let ![$K \in C \big( [0, 1] \times [0, 1] \big)$](../../assets/latex/analysis_75b1515e39d70fb6460af8c4ac8706dc60ef8021.png) be what's called a kernel on
be what's called a kernel on ![$C([0, 1])$](../../assets/latex/analysis_d0a786318a6f7e61dfb7af9b501295ff0c1a81b9.png) and let
and let
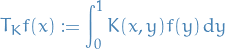
called a integral operator of  .
.
Then
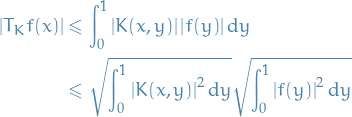
which implies that

That is,

So  is bounded and
is bounded and  .
.
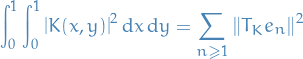
Let ![$H = L^2([0 , 1])$](../../assets/latex/analysis_afd7879552e1e7d31d0443706916f151a99a722f.png) be the completion of
be the completion of ![$\big( C([0, 1]), \left\langle \cdot, \cdot \right\rangle \big)$](../../assets/latex/analysis_e0d8221cd60c2ff589c97c3554435a7f82568a95.png) .
.
Consider the ONB defined by the Fourier coefficients  .
.
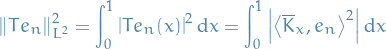
where
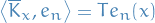
Summing over 
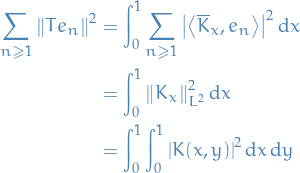
Compact operators
Notation
 denotes the space of compact operators
denotes the space of compact operators , i.e. denotes the set of all convergent sequences
, i.e. denotes the set of all convergent sequences
Stuff
Let  and
and  be normed spaces and let
be normed spaces and let  .
.
Then  is said to be a compact operator if
is said to be a compact operator if  is a compact subset of
is a compact subset of  .
.
That is,  is compact if the image of the unit closed ball is compact.
is compact if the image of the unit closed ball is compact.
Recall that in finite-dimensional space, by Heine Borel, closed and bounded subsets are compact.
Hence finite-rank operators are always compact!
Suppose that  is a normed space,
is a normed space,  is a Banach space and that
is a Banach space and that  is a compact operator.
is a compact operator.
Suppose there is a 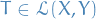 s.t.
s.t.  as
as  . Then
. Then  is compact.
is compact.
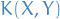 is a subspace of
is a subspace of 
- If
 is a Banach space, then
is a Banach space, then 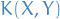 is closed (i.e. Theorem thm:limit-of-compact-operators-is-compact since it contains all its limit points)
is closed (i.e. Theorem thm:limit-of-compact-operators-is-compact since it contains all its limit points)
- Supose
 are separable Hilbert spaces (thus there exist bases)
are separable Hilbert spaces (thus there exist bases) We have

- Though we will only prove

- Though we will only prove
- Let
 linear and
linear and 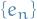 be a ONB in
be a ONB in  , and assume
, and assume  since otherwise "containments" would be equality for all in the above.
since otherwise "containments" would be equality for all in the above. Furthermore, suppose
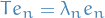
 iff
iff  and
and  , since
, since
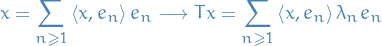
 iff
iff  and
and 
 iff
iff 
 iff
iff 
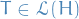 iff
iff 
From this we get the above sequence of containments, since

Spectral Theorem for Bounded Self-Adjoint Operators
Notation
 is the separable complex Hilbert space
is the separable complex Hilbert spaceOperator norm of
 on
on  is
is

is finite.
- Banach space of bounded operators on
 , wrt. operator norm is denoted
, wrt. operator norm is denoted  .
.  denotes the resolvent set of
denotes the resolvent set of 
 denotes the spectrum of
denotes the spectrum of 
 denotes the projection-valued measure associated with the operator self-adjoint
denotes the projection-valued measure associated with the operator self-adjoint 
For any projection-vauled measure
 and
and  , we have an ordinary (positive) real-valued measure
, we have an ordinary (positive) real-valued measure  given by
given by

 is a map defined by
is a map defined by
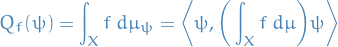
Spectral subspace for each Borel set


of

 defines a simultanouesly orthonormal basis for a family
defines a simultanouesly orthonormal basis for a family 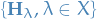 of separable Hilbert spaces
of separable Hilbert spaces
Properties of Bounded Operators
Linear operator
 on
on  is said to be bounded if the operator norm of
is said to be bounded if the operator norm of 

is finite.
Space of bounded operators on
 forms a Banach space under the operator norm, and we have the inequality
forms a Banach space under the operator norm, and we have the inequality

for all bounded operators on
 and
and  .
.
For 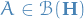 , the resolvent set of
, the resolvent set of  , denoted
, denoted  is the set of all
is the set of all  such that the operator
such that the operator 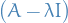 has a bounded inverse.
has a bounded inverse.
The spectrum of  , denoted by
, denoted by  , is the complement in
, is the complement in  of the resolvent set.
of the resolvent set.
For  in the resolvent set of
in the resolvent set of  , the operator
, the operator  is called the resolvent of
is called the resolvent of  at
at  .
.
Alternatively, the resolvent set of  can be described as the set of
can be described as the set of  for which
for which 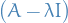 is one-to-one and onto.
is one-to-one and onto.
For all 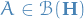 , the following results hold.
, the following results hold.
- The spectrum
 of
of  is closed, bounded and nonempty subset of
is closed, bounded and nonempty subset of  .
. - If
 , then
, then  is in the resolvent set of
is in the resolvent set of 
Point 2 in proposition:hall13-quant-7.5 establishes that  is bounded if
is bounded if  is bounded.
is bounded.
Suppose 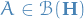 satisfies
satisfies  .
.
Then the operator 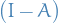 is invertible, with the inverse given by the following convergent series in
is invertible, with the inverse given by the following convergent series in  :
:

For all 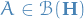 , we have
, we have
![\begin{equation*}
\big[ \text{Range}(A) \big]^{\perp} = \text{ker}(A^*)
\end{equation*}](../../assets/latex/analysis_041fde8f7e956e923e6e23df6a01ead0a29b2641.png)
Spectral Theorem for Bounded Self-Adjoint Operators
Given a bounded self-adjoint operator  , we hope to associate with each Borel set
, we hope to associate with each Borel set 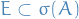 a closed subspace
a closed subspace  of
of  , where we think intuitively that
, where we think intuitively that  is the closed span of the generalized eigenvectors for
is the closed span of the generalized eigenvectors for  with eigenvalues in
with eigenvalues in  .
.
We would expect the following properties of these subspaces:
 and
and 
- Captures idea that generalized eigenvectors should span

- Captures idea that generalized eigenvectors should span
- If
 and
and  are disjoint, then
are disjoint, then 
- Generalized eigenvectors ought to have some sort of orthogonality for distinct eigenvalues (even if not actually in
 )
)
- Generalized eigenvectors ought to have some sort of orthogonality for distinct eigenvalues (even if not actually in
- For any
 and
and  ,
, 
If
 are disjoint and
are disjoint and  , then
, then
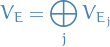
- For any
 ,
,  is invariant under
is invariant under  .
. If
![$E \subset [\lambda_0 - \varepsilon, \lambda_0 + \varepsilon]$](../../assets/latex/analysis_bec5a95e47e8417fb8c1111121dd55490ad968ee.png) and
and  , then
, then

Projection-Valued measures
For any closed subspace  , there exists a unique bounded operator
, there exists a unique bounded operator  such that
such that

where  is the orthogonal complement.
is the orthogonal complement.
This operator is called the orthogonal projection onto  and it satisfies
and it satisfies

i.e. it's self-adjoint.
One also has the properties

or equivalently,
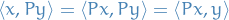
Conversely, if  is any bounded operator on
is any bounded operator on  satisfying
satisfying 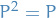 and
and 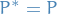 , then
, then  is the orthogonal projection onto a closed subspace
is the orthogonal projection onto a closed subspace  , where
, where

- Convenient ot describe closed subspaces of
 in terms of associated orthogonal projection operators
in terms of associated orthogonal projection operators - Projection operator expresses the first four properties of the spectral subspaces; those properties are similar to those of a measures, so we use the term projection-valued measure
Let  be a set and
be a set and  an
an 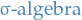 in
in  .
.
A map  is called a projection-valued measure if the following properties are satisfied:
is called a projection-valued measure if the following properties are satisfied:
- For each
 ,
,  is an orthogonal projection
is an orthogonal projection  and
and 
If
 are disjoint, then for all
are disjoint, then for all  , we have
, we have
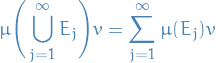
where the convergence of the sum is in the norm-topology on
 .
.
- For all
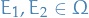 , we have
, we have 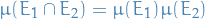
Properties 2 and 4 in of a projection-valued measure tells us that if  and
and  are disjoint, then
are disjoint, then

from which it follows that the range of  and the range of
and the range of  are perpendicular.
are perpendicular.
Let  be a
be a  in a set
in a set  and let
and let  be a projection-valued measure.
be a projection-valued measure.
Then there exists a unique linear map, denoted
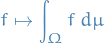
from the space of bounded, measurable, complex-valued functions on  into
into  with the property that
with the property that

for all  and all
and all  .
.
This integral has the following properties:
For all
 , we have
, we have
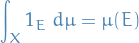
In particular, the integral of the constant function
 is
is  .
.
For all
 , we have
, we have

Integration is multiplicative: For all
 and
and 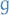 , we have
, we have
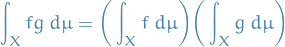
For all
 , we have
, we have
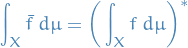
In particular, if
 is real-valued, then
is real-valued, then  is self-adjoint.
is self-adjoint.
By Property 1 and linearity, integration wrt.  has the expected behavior on simple functions. It then follows from Property 2 that the integral of an arbitrary bounded measurable function
has the expected behavior on simple functions. It then follows from Property 2 that the integral of an arbitrary bounded measurable function  can be comptued as follows:
can be comptued as follows:
- Take sequence
 of simple functions converging uniformly to
of simple functions converging uniformly to 
- The integral of
 is then the limit, in the norm-topology, of the integral of the
is then the limit, in the norm-topology, of the integral of the  .
.
A quadratic form on a Hilbert space  is a map
is a map  with the following properties:
with the following properties:
 for all
for all  and
and 
the map
 defined by
defined by
![\begin{equation*}
\begin{split}
L(\phi, \psi) =& \frac{1}{2} \big[ Q(\phi + \psi) - Q(\phi) - Q(\psi) \big] \\
& - \frac{i}{2} \big[ Q(\phi + i \psi) - Q(\phi) - Q(i \psi) \big]
\end{split}
\end{equation*}](../../assets/latex/analysis_6085b0f14f4edf2b5f0f23825c97cba9ce1cc8de.png)
is a sesquilinear form.
A quadratic form  is bounded if there eixsts a constant
is bounded if there eixsts a constant  such that
such that

The smallest such constant  is the norm of
is the norm of  .
.
If  is a bounded quadratic form on
is a bounded quadratic form on  , there is a unique
, there is a unique 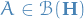 such that
such that

If  belongs to
belongs to  for all
for all  , then the operator
, then the operator  is self-adjoint.
is self-adjoint.
Spectral Theorem for Bounded Self-Adjoint Operators: direct integral approach
Notation
 is a
is a  measure on a
measure on a 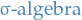
 of sets in
of sets in 
- For each
 we have a separable Hilbert space
we have a separable Hilbert space  with inner product
with inner product 
- Elements of the direct integral are called sections

Stuff
There are several benefits to this approach compared to the simpler "multiplication operator" approach.
- The set
 and the function
and the function  become canonical:
become canonical:
- The direct integral carries with it a notion of generalized eigenvectors / kets, since the space
 can be thought of as the space of generalized eigenvectors with eigenvalue
can be thought of as the space of generalized eigenvectors with eigenvalue  .
. - A simple way to classify self-adjoint operators up to unitary equivalence: two self-adjoint operators are unitarily equivalent if and only if their direct integral representations are equivalent in a natural sense.
Elements of the direct integral are called sections  , which are functions on
, which are functions on  with values in the union of the
with values in the union of the  , with property
, with property
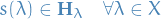
We define the norm of a section  by the formula
by the formula

provided that the integral on the RHS is finite.
The inner product between two sections 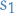 and
and  (with finite norm) should then be given by the formula
(with finite norm) should then be given by the formula
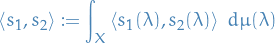
Seems very much like the differential geometry section we know of.
 is the fibre at each point
is the fibre at each point  in the mfd.
in the mfd. is the mfd.
is the mfd.
First we slightly alter the concept of an orthonormal basis. We say a family  of vectors is an orthonormal basis for a Hilbert space
of vectors is an orthonormal basis for a Hilbert space  if
if

and

This just means that we allow some of the vectors in our basis to be zero.
We define a simultanouesly orthonormal basis for a family  of separable Hilbert spaces to be a collection
of separable Hilbert spaces to be a collection  of sections with the property that
of sections with the property that

Provided that the function  is a measurable function from
is a measurable function from  into
into ![$[0, \infty]$](../../assets/latex/analysis_7c43cf12221cf82ea0f3550c49639ade5528d224.png) , it is possible to choose a simultaneous orthonormal basis
, it is possible to choose a simultaneous orthonormal basis  such that
such that

is measurable for all  and
and  .
.
Choosing a simultaneous orthonormal basis with the property that the function

is a measurable function from  into
into ![$[0, \infty]$](../../assets/latex/analysis_7c43cf12221cf82ea0f3550c49639ade5528d224.png) , we can define a section to be measurable if the function
, we can define a section to be measurable if the function

is a measurable complex-valued function for each  . This also means that the
. This also means that the  are also measurable sections.
are also measurable sections.
We refer to such a choice of simultaneous orthonormal basis as a measurability structure on the collection  .
.
Given two measurable sections 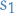 and
and  , the function
, the function
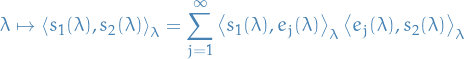
is also measurable.
Suppose the following structures are given:
- a
 measure space
measure space 
- a collection
 of separable Hilbert spaces for which the dimension function is measurable
of separable Hilbert spaces for which the dimension function is measurable - a measurability structure on

Then the direct integral of  wrt.
wrt.  , denoted
, denoted

is the space of equivalence classes of almost-everywhere-equal measurable sections  for which
for which

The inner product 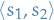 of two sections
of two sections 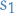 and
and  is given by the formula
is given by the formula

If 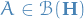 is self-adjoint, then there exists a σ-finite measure
is self-adjoint, then there exists a σ-finite measure  on
on  , a direct integral
, a direct integral

and a unitary map  between
between  and the direct integral such that
and the direct integral such that

for all sections  .
.
Proofs
Notation
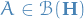 with spectral radius
with spectral radius
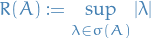
Stage 1: Continuous Functional Calculus
Stage 2: An Operator-Valued Riesz Representation Theorem
Let  be a compact metric space and let
be a compact metric space and let  denote the space of continuous, real-valued functions on
denote the space of continuous, real-valued functions on  .
.
Suppose 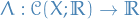 is a linear functional with the property that
is a linear functional with the property that  is non-negative if
is non-negative if  is non-negative.
is non-negative.
Then there exists a unique (real-valued, positive) measure  on the Borel sigma-algebra in
on the Borel sigma-algebra in  for which
for which
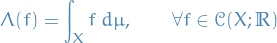
Observe that  is a finite measure, with
is a finite measure, with

where  is the constant function.
is the constant function.
Continuous one-parameter groups
 semigroup or strongly continuous one-parameter semigroup
semigroup or strongly continuous one-parameter semigroup
A strongly continuous one-parameter semigroup on a Banach space  is a map
is a map  such that
such that
 (i.e.
(i.e.  identity operator on
identity operator on 
 we have
we have

 we have
we have

The first two axioms are algebraic, and state  is a representation of a semigroup
is a representation of a semigroup  , and the last axiom is topological and states that
, and the last axiom is topological and states that  is continuous in the strong operator topology.
is continuous in the strong operator topology.
Infinitesimal generator
The infinitesimal generator  of a strongly continuous semigroup
of a strongly continuous semigroup  defined by
defined by

whenever the limit exists.
The domain of  , denoted
, denoted  , is the set of
, is the set of  for which the limit does exist;
for which the limit does exist;  is a linera subspace and
is a linera subspace and  is linear on this domain.
is linear on this domain.
The operator  is closed, although not necessarily bounded, and the domain
is closed, although not necessarily bounded, and the domain  is dense in
is dense in  .
.
The storngly continuous semigroup  with generator
with generator  is often denoted by the symbol
is often denoted by the symbol  , which is compatible with the notation for matrix exponentials.
, which is compatible with the notation for matrix exponentials.
Reproducing Kernel Hilbert Spaces (RKHSs)
Definitions
Let  be a non-empty set, sometimes reffered to as the index set.
be a non-empty set, sometimes reffered to as the index set.
A symmetric function  is called a positive-definite kernel of
is called a positive-definite kernel of  if
if

holds for any  ,
, 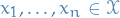 ,
,  .
.
Or more generally, for some field real or complex field  , a function
, a function  is called a kernel on
is called a kernel on  if there exists a
if there exists a  and a map
and a map  such that for all
such that for all  we have
we have

In machine learning context, you'll often see  be called a feature map and
be called a feature map and  a feature space of
a feature space of  .
.
The definition of a positive-definite kernel is equivalent to the following: A symmetric function  is positive-definite if the matrix
is positive-definite if the matrix  with elements
with elements
![\begin{equation*}
\big[ k_{X X} \big]_{ij} = k(x_i, x_j)
\end{equation*}](../../assets/latex/analysis_552698d082ca0fca2447a0726f58904d0e84c322.png)
is positive semi-definite for any finite set  of any size
of any size  .
.
This matrix  is often referred to as the kernel matrix or Gram matrix.
is often referred to as the kernel matrix or Gram matrix.
Note the swapping of order in the kernel and inner product above; this is only necessary in the case of a complex Hilbert space, where the inner product is sesquilinear:
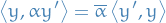
Examples of kernels
Let
Then a Gaussian RBF kernel or square exponential kernel is defined
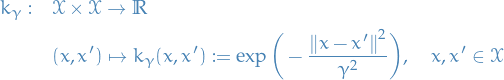
Let
The Matérn kernel is defined
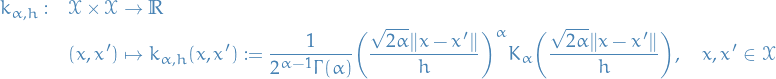
where
 is the gamma-function
is the gamma-function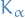 is the modified Bessel function of the second kind of order
is the modified Bessel function of the second kind of order 
 determines the scale
determines the scale determines the smoothness of the functions in the associated RKHS
determines the smoothness of the functions in the associated RKHS
- As
 increases, the functions get smoother
increases, the functions get smoother
- As
If  can be written as
can be written as
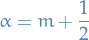
for  , then the expression for the Matérn kernel reduces to a product of the exponentiated function and a polynomial of degree
, then the expression for the Matérn kernel reduces to a product of the exponentiated function and a polynomial of degree  , which can be computed easily rasmussen2006gaussian:
, which can be computed easily rasmussen2006gaussian:
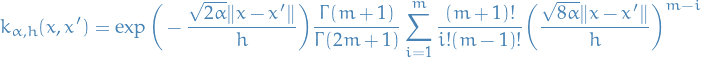
For example 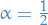 results in whats know as the Laplace or exponentiated kernel:
results in whats know as the Laplace or exponentiated kernel:
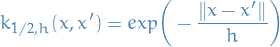
Gaussian RBF kernels can be obtained as limits of Matérn kernels for  , i.e. for a Matérn kernel
, i.e. for a Matérn kernel  with
with  being fixed, we have
being fixed, we have
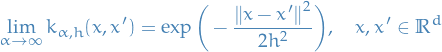
Let
Then a polynomial kernel is defined
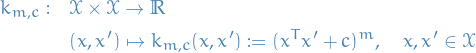
TODO Kernel embeddings
Exam prep
May 2017
1
c
If  uniformly continuous, and
uniformly continuous, and  uniformly then
uniformly then  is also uniformly continuous.
is also uniformly continuous.
Given  , find
, find  such that
such that
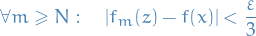
In particular 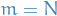 ,
,

 is uniformly continuous, implies
is uniformly continuous, implies


Compactness
 ,
,  is closed and
is closed and  is compact, then
is compact, then  is also compact.
is also compact.
Let  be any open cover of
be any open cover of  .
.
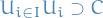
 might not cover whole
might not cover whole  .
.  is open, therefore
is open, therefore

is an open cover of  . Thus, due to
. Thus, due to  being compact, there exists a finite subcover of the above cover,
being compact, there exists a finite subcover of the above cover,

covers  , then clearly
, then clearly 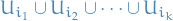 is a finite cover of
is a finite cover of  , hence
, hence  is compact, as claimed.
is compact, as claimed.
Proving connectedness of a set
- Best way to prove a set
 is connected is to check if it's path connected
is connected is to check if it's path connected - Best way to prove a set
 is not connected (disconnected), we use the definition of connectedness:
is not connected (disconnected), we use the definition of connectedness:
Find 2 open sets
 such that
such that

i.e. two sets such that the union covers
 but they share no elements.
but they share no elements.

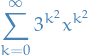
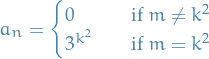
 as the common value
as the common value


 outside of
outside of ![\begin{equation*}
\big( \exp f \big) \chi_{[a, b]}
\end{equation*}](../../assets/latex/analysis_e375644fca83d837ca4ae811adda2aceb0c8a29f.png)
 is said to be open if and only if for every
is said to be open if and only if for every  there is an
there is an  is contained in
is contained in  is
is 

 .
.
 .
.