Algebra
Table of Contents
Notation
 denotes a group
denotes a group- CANI stands for:
- Commutative
- Associative
- Neutral element (e.g. 0 for addition)
- Inverse
Terminology
- almost all
- is an abbreviation meaning "all but finitely many"
Definitions
Homomorphisms
A homomorphism  is a structure-preserving map between the groups
is a structure-preserving map between the groups  and
and  , i.e.
, i.e.

A endomorphism is a homomorphism from the group  to itself, i.e.
to itself, i.e. 
Linear isomorphism
Two vector spaces  and
and 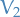 are said to be isomorphic if and only if there exists a linear bijection
are said to be isomorphic if and only if there exists a linear bijection 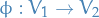 .
.
Field
An (algebraic) field  is a set
is a set  and the maps
and the maps
that satisfy

Vector space
A vector space  over a field
over a field  is a pair consisting of an abelian group
is a pair consisting of an abelian group  and a mapping
and a mapping

such that for all  and
and 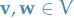 we have A D D U:
we have A D D U:
- Associativity:

- Distributivity over field-addition:
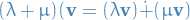
- Distributivity over field-multiplication:

- Uint:

Ring
Equivalence relations
A equivalence relation on some set is defined as some relation betweeen  and
and  , denoted
, denoted  , such that the relation is:
, such that the relation is:
- reflexive:

- symmetric:
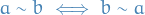
- transistive

Why do we care about these?
- Partitions the set it's defined on into unique and disjoint subsets
Unitary transformations
A unitary transformation is a transformation which preserves the inner product.
More precisely, a unitary transformation is an isomorphism between two Hilbert spaces.
Groups
Notation
![$[G : H]$](../../assets/latex/algebra_113a390f333ef98f5d83a6bd467913647b2d6881.png) or
or  denotes the number of left cosets of a subgroupd
denotes the number of left cosets of a subgroupd  of
of  , and is called the index
, and is called the index
Definitions
The symmetric group  of a finite set of
of a finite set of  symbols is the group whose elements are all the permutation operations that can be performed on the
symbols is the group whose elements are all the permutation operations that can be performed on the  distinct symbols, and whose group operation is the composition of such permutation operations, which are defined as bijective functions from the set of symbols to itself.
distinct symbols, and whose group operation is the composition of such permutation operations, which are defined as bijective functions from the set of symbols to itself.
An action of a group is a formal way of interpreting the manner in which the elements of the group correspond to transformations of some space in a way that preserves the structure of the space.
If  is a group and
is a group and  is a set, then a (left) group action
is a set, then a (left) group action  of
of  on
on  is a function
is a function
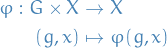
that satisfies the following two axioms (where we denote  as
as  ):
):
- identity:
 for all
for all  (
( denotes the identity element of
denotes the identity element of  )
) - compatibility:
 for all
for all  and all
and all 
where  denotes the result of first applying
denotes the result of first applying  to
to  and then applying
and then applying 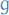 to the result.
to the result.
From these two axioms, it follows that for every  , the function
, the function  which maps
which maps  to
to  is a bijective map from
is a bijective map from  to
to  . Therefore, one may alternatively define a group action of
. Therefore, one may alternatively define a group action of  on
on  as a group homomorphism from
as a group homomorphism from  into the symmetric group
into the symmetric group 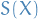 of all bijections from
of all bijections from  to
to  .
.
The action of  on
on  is called transistive if
is called transistive if  is non-empty and if:
is non-empty and if:
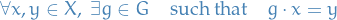
Faithful (or effective ) if

That is, in a faithful group action, different elements of  induce different permutations of
induce different permutations of  .
.
In algebraic terms, a group  acts faithfully on
acts faithfully on  if and only if the corresponding homomorphism to the symmetric group,
if and only if the corresponding homomorphism to the symmetric group,  , has a trivial kernel.
, has a trivial kernel.
If  does not act faithfully on
does not act faithfully on  , one can easily modify the group to obtain a faithful action. If we define:
, one can easily modify the group to obtain a faithful action. If we define:

then  is the normal subgroup of
is the normal subgroup of  ; indeed, it is the kernel of the homomorphism
; indeed, it is the kernel of the homomorphism  . The factor group
. The factor group 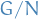 acts faithfully on
acts faithfully on  by setting
by setting 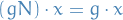 .
.
We say a group action is free (or semiregular or fixed point free ) if, given  ,
,

We say a group action is regular if and only if it's both transitive and free; that is equivalent to saying that for every two  there exists precisely one
there exists precisely one  s.t.
s.t. 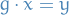 .
.
Consider a group  acting on a set
acting on a set  . The orbit of an element
. The orbit of an element  in
in  is the set of elements in
is the set of elements in  to which
to which  can be moved by the elements of
can be moved by the elements of  . The orbit of
. The orbit of  is denoted by
is denoted by 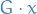 :
:
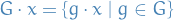
An abelian group, or commutative group, is simply a group where the group operation is commutative!
A monoid is an algebraic structure with a single associative binary operation and an identity element, i.e. it's a semi-group with a binary operation.
Cosets
Let  be a group and
be a group and  be a subgroup of
be a subgroup of  . Let
. Let  . The set
. The set

of products of 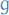 with elements of
with elements of  , with
, with 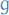 on the left is called a left coset of
on the left is called a left coset of  in
in  .
.
The number of left cosets of a subgroup  of
of  is the index of
is the index of  in
in  and is denoted by
and is denoted by 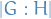 or
or ![$[G : H]$](../../assets/latex/algebra_113a390f333ef98f5d83a6bd467913647b2d6881.png) . That is,
. That is,
![\begin{equation*}
[G : H] = \left| G / H \right|
\end{equation*}](../../assets/latex/algebra_b04fe081606903544e6cfd4f4c4eda2f4b142fe8.png)
Center
Given a group  , the center of
, the center of  , denoted
, denoted  is defined as the set of elements which commute with every element of the group, i.e.
is defined as the set of elements which commute with every element of the group, i.e.

We say that a subgroup  of
of  is central if it lies inside
is central if it lies inside  , i.e.
, i.e. 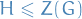 .
.
Abelianisation
Given a group  , define a abelianisation of
, define a abelianisation of  to be the quotient group
to be the quotient group

with  is the normal subgroup generated by the commutators
is the normal subgroup generated by the commutators 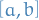 for
for  , i.e.
, i.e.
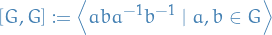
Theorems
Let  be a group of order
be a group of order  and let
and let 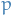 be a prime divison of
be a prime divison of  .
.
Then  has an element of order
has an element of order 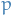 .
.
Fermat's Little Theorem
Let 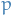 be a prime number.
be a prime number.
Then for  , the number
, the number 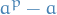 is an integer multiple of
is an integer multiple of 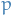 . That is
. That is

Isomorphism theorems
Let
 be a group homomorphism
be a group homomorphism
Then 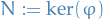 is a normal subgroup of
is a normal subgroup of  , and
, and  . Furthermore, there is an isomorphim
. Furthermore, there is an isomorphim

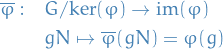
In particular, if  is surjective, then
is surjective, then

Le  be a group,
be a group,  and
and  .
.
First
 so clearly
so clearly  .
Let
.
Let 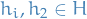 and
and 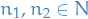 . We then want to show that
. We then want to show that  .
Observe that
.
Observe that
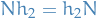
since
 .
So
.
So 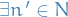 so that
so that  ,
,

And now we check that the
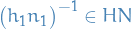

Let
 ,
,  . Wan to show that
. Wan to show that  .
.

- Let
 ,
,  . Then
. Then  since
since  , so
, so  , for all
, for all  .
. Want to show that
 .
First Isomorphism Theorem tells us that
.
First Isomorphism Theorem tells us that
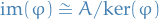
Therefore, letting

where we simply factor out the
 from every element in
from every element in  .
.

So
 maps into
maps into 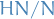 , but we need it to be surjective, i.e.
, but we need it to be surjective, i.e.

An element of
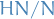 is a coset
is a coset  for
for  , which is clearly
, which is clearly  . And finally,
. And finally,
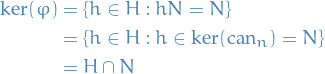
Hence, by the First Isomorphism Theorem,

Notice  . In fact,
. In fact,  .
.
As an example, 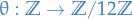 . Then
. Then

by the First Isomorphism Theorem and since  .
And, we can also write
.
And, we can also write
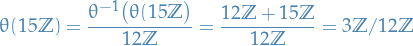
since  .
.
Want to show that both are isom. to 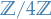 . We do this by constructing map:
. We do this by constructing map:
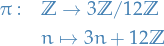
and just take the coset. And,
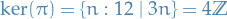
Hence by 1st Isom. Thm.
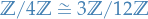
Kernels and Normal subgroups
Arising from an action  of a group
of a group  on a set
on a set  , is the homomorphism
, is the homomorphism
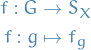
the permutation of  corresponding to
corresponding to 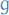 .
.
The kernel of this homomorphism is also called the kernel of the action  and is denoted
and is denoted  .
.
Remember,

is the permutation 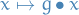 . Therefore,
. Therefore,  if and only if
if and only if  for all
for all  , and so
, and so
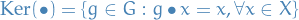
consists of those elements which stabilize every element of  .
.
Let  be a subgroup of a group
be a subgroup of a group  , and let
, and let  .
.
The conjugate of  by
by  , written
, written  , is the set
, is the set

of all conjugate of elements of  by
by  .
.
This is the image  of
of  under the conjugation homomorphism
under the conjugation homomorphism  where
where  .
.
Hence,  is a subgroup of
is a subgroup of  .
.
Let  be a subgroup of
be a subgroup of  .
.
If  for all
for all  , then
, then

A subgroup  of a group,
of a group,  , is called a normal subgroup if it is invariant under conjugation; that is, the conjugation of an element of
, is called a normal subgroup if it is invariant under conjugation; that is, the conjugation of an element of  by an element of
by an element of  is still in
is still in  :
:

 . Then
. Then  if and only if
if and only if  for all
for all  .
.
Let  and
and  be groups.
be groups.
The kernel of any homomorphism 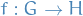 is normal in
is normal in  .
.
Hence, the kernel of any group action of  is normal in
is normal in  .
.
Let  be a group acting on the set
be a group acting on the set  of left cosets of a subgroup
of left cosets of a subgroup  of
of  .
.
- The stabilizer of each left coset
 is the conjugate
is the conjugate 
- If
 for all
for all  then
then 
Factor / Quotient groups
Let  be a group acting on a set
be a group acting on a set  and
and  be the kernel of the action.
be the kernel of the action.
The set of cosets of  in
in  is a group with binary operation
is a group with binary operation

which defines the factor group or quotient group of  by
by  and is denoted
and is denoted
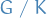
But I find the following way of defining a quotient group more "understandable":
Let  be a group homomorphism such that
be a group homomorphism such that
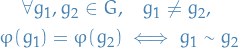
That is,  maps all distinct
maps all distinct  which are equivalent under
which are equivalent under  to the same element in
to the same element in  , but still preserves the group structure by being a homomorphism of groups.
, but still preserves the group structure by being a homomorphism of groups.
There is a function  with
with

For  we have that
we have that

thus  is a homomorphism.
is a homomorphism.
Then, clearly

 is called the natural homomorphism from
is called the natural homomorphism from  to
to 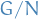 .
.
Group presentations
Notation
 or
or  refers to the group generated by
refers to the group generated by  such that
such that 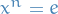
 denote is the free group as generated by
denote is the free group as generated by 
In general:
 , e.g.
, e.g.
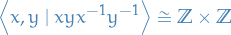
where the "unit-condition" simply specifies that the group is commutative
Free groups
 is the free group generated by
is the free group generated by  .
.
Elements are symbols in  , subject to
, subject to
- group axioms
- " and all logical consequences :) "
Let  .
.
The group with presentation
is the group generated by  subject to
subject to
- group axioms

- " and all logical consequences :) "
There's no algorithm for deciding whether  is the trivial group.
is the trivial group.
Let  and let
and let  , where
, where  is a group.
is a group.
Then there is a unique homomorphism:

And the image of  is the subgroup of
is the subgroup of  generated by
generated by  .
.
Central Extensions of Groups
Let
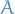 be an abelian group
be an abelian group be an arbitrary group
be an arbitrary group
An extension of  by the group
by the group 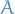 is given an exact sequence of group homomorphisms
is given an exact sequence of group homomorphisms

The extension is called central if 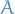 is abelian and its image
is abelian and its image  , where
, where  denotes the center of
denotes the center of  , i.e.
, i.e.

For a group  acting on another group
acting on another group  by a homomorphism
by a homomorphism  , the semi-direct product group
, the semi-direct product group  is the set
is the set  with the multiplication given by the formula
with the multiplication given by the formula

This is a special case of a group extension with  and
and  :
:

Exact sequence
An exact sequence of groups is given by

of groups and group homomorphisms, where exact refers to the fact that
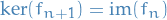
Linear Algebra
Notation
 denotes the set of all matrices on the field
denotes the set of all matrices on the field 
![$M_\mathcal{B}^\mathcal{A} = {}_\mathcal{B}[f]_\mathcal{A}$](../../assets/latex/algebra_1a3e01cd9b152a4a99ee466373fc7699987ae513.png) denotes the representing matrix of the mapping
denotes the representing matrix of the mapping  wrt. bases
wrt. bases  and
and  , where
, where  is ordered basis for
is ordered basis for  and
and  ordered basis for
ordered basis for 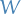 :
:
![\begin{equation*}
{}_\mathcal{B}[f]_\mathcal{A} = {}_\mathcal{B}[f]_{\mathcal{B}} \circ {}_{\mathcal{B}}\text{id}_{\mathcal{A}} \circ {}_\mathcal{A}[f]_\mathcal{A}
\end{equation*}](../../assets/latex/algebra_4e130107b602d6cee146ac936051ccb2fb027981.png)
![${}_\mathcal{B}[f] = {}_{\mathcal{B}}\text{id} [f]$](../../assets/latex/algebra_0523db315c405d3dbc83dcb0ab9de97b988670c7.png) and
and ![$[f]_{\mathcal{B}} = [f] \text{id}_{\mathcal{B}}$](../../assets/latex/algebra_9b4615d88f6ccbc4460b13a1862bb2f7f32c8e1f.png) where
where  denotes the "identity-mapping" from elements represented in the basis
denotes the "identity-mapping" from elements represented in the basis  to the representation in
to the representation in  .
. denotes the n-dimensional standard basis
denotes the n-dimensional standard basis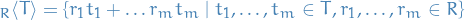
 , i.e. the set of non-zero elements of
, i.e. the set of non-zero elements of 
Vector Spaces
Notation
 is a set
is a set is a field
is a field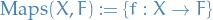

Basis
A subset of a vector space is called a generating set of the vector space if its span is all of the vector space.
A vector space that has a finite generating set is said to be finitely generated.
 is called linearly independent if for all pairwise different vectors
is called linearly independent if for all pairwise different vectors 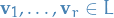 and arbitrary scalars
and arbitrary scalars 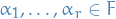 ,
,
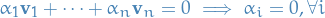
A basis of a vector space  is a linearly independent generating set in
is a linearly independent generating set in  .
.
The following are equivalent for a subset of  for a bector space
for a bector space  :
:
 is a basis, i.e. linearly independent generating set
is a basis, i.e. linearly independent generating set is minimal among all generating sets, i.e.
is minimal among all generating sets, i.e.  does not generate
does not generate  for any
for any 
 is maximal among all linearly independent subsets, i.e.
is maximal among all linearly independent subsets, i.e.  is not lineraly independent for any
is not lineraly independent for any  .
.
"Minimal" and "maximal" refers to the inclusion and exclusion.
Let  be a vector space containing vector subspaces
be a vector space containing vector subspaces 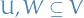 . Then
. Then

Linear mappings
Let 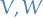 be vector spaces over a field
be vector spaces over a field  . A mapping
. A mapping  is called linear or more precisely
is called linear or more precisely  linear if
linear if
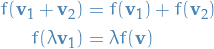
This is also a homomorphism of vector spaces.
Let  be a linear mapping between vector spaces. Then,
be a linear mapping between vector spaces. Then,

where usually we use the terminology:
- rank of
 is
is 
- nullity of
 is
is 
Linear Mappings and Matrices
Let  be a field and let
be a field and let  .
.
There exists a bijection  and set of matrices with
and set of matrices with  rows and
rows and  columns:
columns:
![\begin{equation*}
\begin{split}
M: \text{Hom}_F(F^M, F^n) & \overset{\sim}{\to} \text{Mat}(n \times m; F) \\
f &\mapsto [f]
\end{split}
\end{equation*}](../../assets/latex/algebra_39c17a263e9fbcb91b2cb228766db36df4a26d2f.png)
Which attaches to each linear mapping  , its representing matrix
, its representing matrix ![$M(f) := [f]$](../../assets/latex/algebra_65a75e0c78a4b206d062ea3b411f7a65611f94bf.png) , defined
, defined
![\begin{equation*}
[f] :=
\begin{pmatrix}
f(\mathbf{e}_1) & f(\mathbf{e}_2) & \dots & f(\mathbf{e}_m)
\end{pmatrix}
\end{equation*}](../../assets/latex/algebra_75ed773544a3456b1521a482b8b595409106e096.png)
i.e. the matrix-representation of  is a defined by how
is a defined by how  maps the basis of the target space.
maps the basis of the target space.
Observe that the matrix product between two matrices ![$A = [f]$](../../assets/latex/algebra_ce6900a7bef6f5274e33532d2609a40e826a1c13.png) and
and ![$B = [g]$](../../assets/latex/algebra_b68a095d4020c81ac65f4ffc446e4db613c4e15e.png) ,
,
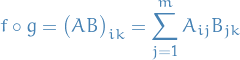
An elementary matrix is any square matrix which differs from the identity matrix in at most one entry.
Any matrix whose only non-zero entries lie on the diagonal, and which has the first 1's along the diagonal and then 0's elsewhere, is said to be in Smith Normal Form
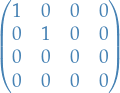
 there exists invertible matrices
there exists invertible matrices  and
and  s.t.
s.t.  is a matrix in Smith Normal Form.
is a matrix in Smith Normal Form.
A linear mapping  is injective if and only if
is injective if and only if

Let 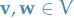 , then
, then

Hence, if

as claimed.
Let  be square matrices over some commutative ring
be square matrices over some commutative ring  are conjugate if
are conjugate if

for an invertible P ∈ (n; R).
Further, conjugacy is an equivalence relation on  .
.
Trace of linear map
The trace of a matrix 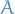 is defined
is defined
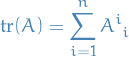
The trace of a finite product of matrices  is independent of the order of the product (given that the products are valid). In other words, trace is invariant under cyclic permutations.
is independent of the order of the product (given that the products are valid). In other words, trace is invariant under cyclic permutations.
To see that trace is a invariant under cyclic permutations, we observe
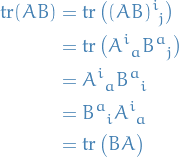
This case of two matrices can easily be generalized to case of products of multiple matrices.
Rings and modules
A ring is a set with two operatiors  that satisfy:
that satisfy:
 is an abelian group
is an abelian group is a monoid
is a monoidThe distributive laws hold, meaning that
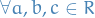 :
:
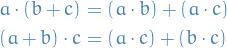
Important: in some places, e.g. earlier in your notes, they use a slightly less restrictive definition of a ring, and in that case we'd call this definition a unitary ring.
Polynomials
A field  is algebraically closed if each non-constant polynomial
is algebraically closed if each non-constant polynomial ![$P \in F[X] \backslash F$](../../assets/latex/algebra_fb886a90b71fbee70f2c8ae6dea3e988584ec0e2.png) with coefficients in
with coefficients in  has a root in
has a root in  .
.
E.g. ![$\mathbb{C}[X]$](../../assets/latex/algebra_e100daaa67a09ac455356a0f05a0572c25ef539d.png) is algebraically closed, while
is algebraically closed, while ![$\mathbb{R}[X]$](../../assets/latex/algebra_40f5f5cfda8e63d360d33282a3238071a3d9e8e4.png) is not.
is not.
If a field  is algebraically closed, then every non-zero polynomial
is algebraically closed, then every non-zero polynomial ![$P \in F[X] \backslash \left\{ 0 \right\}$](../../assets/latex/algebra_41818dd26b791500efbe667651d828fb425a590d.png) decomposes into linear factors
decomposes into linear factors
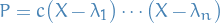
with  ,
,  and
and 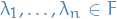 .
.
This decomposition is unique up to reordering of the factors.
Ideals and Subrings
Let  and
and  be rings. A linear map
be rings. A linear map  is a ring homomorphism if the following hold for all
is a ring homomorphism if the following hold for all  :
:
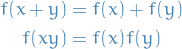
A subset  of a ring
of a ring  is an ideal, written
is an ideal, written  , if the following hold:
, if the following hold:

 is closed under subtraction
is closed under subtraction for all
for all  and
and  , i.e.
, i.e.  closed under multiplication by elements of
closed under multiplication by elements of 
- I.e. we stay in
 even when multiplied by elements from outside of
even when multiplied by elements from outside of 
- I.e. we stay in
Ideals are sort of like normal subgroups for rings!
Let  be a commutative ring and let
be a commutative ring and let  .
.
Then the ideal of  generated by
generated by  is the set
is the set
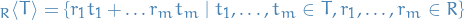
together with the zero element in the case 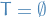 .
.
If  , a finite set, we will often write
, a finite set, we will often write

Let  be a subset of a ring
be a subset of a ring  . Then
. Then  is a subring if and only if
is a subring if and only if
 has a multiplicative identity
has a multiplicative identity is closed under subtraction:
is closed under subtraction: 
 is closed under multiplication
is closed under multiplication
It's important to note that  and
and  does not necessarily have the same identity element, even though
does not necessarily have the same identity element, even though  is a subring of
is a subring of  !
!
Let  be a ring. An element
be a ring. An element  is a called a unit if it's invertible in
is a called a unit if it's invertible in  or in other words has a multiplicative inverse in
or in other words has a multiplicative inverse in  , i.e.
, i.e.
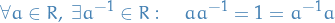
We will use the notation 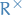 for the group of units of a ring
for the group of units of a ring  .
.
In a ring  a non-zero element
a non-zero element  is called a zero-divisor or divisor of zero if
is called a zero-divisor or divisor of zero if
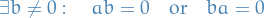
An integral domain is a non-zero commutative ring that has no zero-divisors, i.e.
- If
 then
then 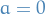 or
or 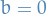
 and
and  then
then 
Factor Rings
Let  be a ring and
be a ring and  and ideal of
and ideal of  .
.
The mapping
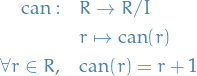
Has the following properties:
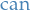 is surjective
is surjectiveIf
 is a ring homomorphism with
is a ring homomorphism with  so that
so that

then there is a unique ring homomorphism:

Where the second point states that  factorizes uniquely through the canonical mapping to the factor whenever the ideal
factorizes uniquely through the canonical mapping to the factor whenever the ideal  is sent to zero.
is sent to zero.
Modules
We say  is a R-module,
is a R-module,  being a ring, if
being a ring, if
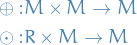
satisfying

Thus, we can view it as a "vector space" over a ring, but because it behaves wildly different from a vector space over a field, we give this space a special name: module.
Important:  denotes a module here, NOT manifold as usual.
denotes a module here, NOT manifold as usual.
A unitary module is in the case where we also have  , i.e. the ring is a unitary ring and contains a multiplicative identity-element.
, i.e. the ring is a unitary ring and contains a multiplicative identity-element.
Let  be a ring and let
be a ring and let  be an R-module. A subset
be an R-module. A subset 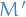 of
of  is a submodule if and only if
is a submodule if and only if
Let  be a ring, let
be a ring, let  and
and  be R-modules and let
be R-modules and let 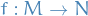 be an R-homomorphism.
be an R-homomorphism.
Then  is injective if and only if
is injective if and only if

Let  . Then
. Then 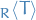 is the smallest submoduel of
is the smallest submoduel of  that contains
that contains  .
.
The intersection of any collection of submodules of  is a submodule of
is a submodule of  .
.
Let  and
and 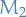 be submodules of
be submodules of  . Then
. Then

is a submodule of  .
.
Let  be a ring,
be a ring,  and R-module and
and R-module and  submodule of
submodule of  .
.
For ever  the coset of
the coset of  wrt.
wrt.  in
in  is
is

It is a coset of  in the abelian group
in the abelian group  and so is an equivalence class for the equivalence relation
and so is an equivalence class for the equivalence relation

The factor of  by
by  or quotient of
or quotient of  by
by  is the set
is the set
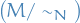
of all cosests of  in
in  .
.
Equipped with addition and s-multiplication
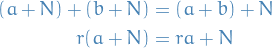
for all  and
and  .
.
The R-module 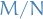 is the factor module of
is the factor module of  by submodule
by submodule  .
.
Let  be a ring, let
be a ring, let  and
and  be R-modules, and
be R-modules, and  a submodule of
a submodule of  .
.
The mapping
 defined by
defined by

is surjective.
If
 is an R-homomorphism with
is an R-homomorphism with

so that
 , then there is a unique homomorphism
, then there is a unique homomorphism  such that
such that  .
.
Let  be a ring and let
be a ring and let  and
and  be R-module. Then every R-homomorphism
be R-module. Then every R-homomorphism 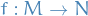 induces an R-isomorphism
induces an R-isomorphism

Let 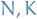 be submodules of a R-module
be submodules of a R-module  .
.
Then  is a submodule of
is a submodule of  and
and  is a submodule of
is a submodule of  .
.
Also,

Let 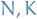 be submodules of an R-module
be submodules of an R-module  , where
, where  .
.
Then 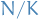 is a submodule of
is a submodule of 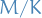 .
.
Also,

Determinants and Eigenvalue Reduction
Definitions
An inversion of a permutation  is a pair
is a pair  such that
such that  and
and  .
.
The number of inversions of the permutation  is called the length of
is called the length of  and writtein
and writtein  .
.
The sign of a permutation  is defined to be the parity of the number of inversions of
is defined to be the parity of the number of inversions of  :
:

where  is the length of the permutation.
is the length of the permutation.
For  , the set of even permutations in
, the set of even permutations in  forms a subgroup of
forms a subgroup of  because it is the kernel of the group homomorphism
because it is the kernel of the group homomorphism 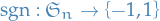 .
.
This group is the alternating group and is denoted  .
.
(X̃ / ker(p))
Let  be a ring.
be a ring.
The determinant is a mapping  given by
given by

Let  be a commutative ring, then
be a commutative ring, then

Let  for some ring
for some ring  , and let
, and let  be the
be the  defined by removing the i-th row and j-th column of
defined by removing the i-th row and j-th column of 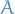 .
.
Then the cofactor matrix  of
of 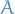 is defined (component-wise)
is defined (component-wise)

The adjugate matrix of 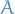 is defined
is defined

where  is the cofactor matrix.
is the cofactor matrix.
The reason for this definition is so that we have the following identity

To see this, recall the "standard" approach to computing the determinant of a matrix 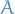 , where we do so by choosing some row
, where we do so by choosing some row  and some column
and some column  , cut out the rest of the matrix, and write the determinant as a expansion in these coefficients. The cofactor matrix has exactly the determinant of that
, cut out the rest of the matrix, and write the determinant as a expansion in these coefficients. The cofactor matrix has exactly the determinant of that  matrix as a entries, hence the above expression is simply going to give us the same expression as the "expansion-method" for computing the determinant.
matrix as a entries, hence the above expression is simply going to give us the same expression as the "expansion-method" for computing the determinant.
Let 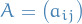 be an
be an  matrix with entries from a commutative ring
matrix with entries from a commutative ring  .
.
For a fixed  the i-th row expansion of the determinant is
the i-th row expansion of the determinant is
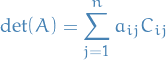
and for a fixed  the j-th column expansion of the determinant is
the j-th column expansion of the determinant is
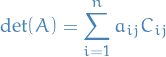
where  is the
is the  cofactor of
cofactor of 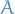
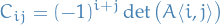
where  is the matrix obtained from deleting the i-th row and j-th column.
is the matrix obtained from deleting the i-th row and j-th column.
Cayley-Hamilton Theorem
Let  be a square matrix with entries in a commutative ring
be a square matrix with entries in a commutative ring  .
.
Then evaluating its characteristic polynomial ![$\chi_A(x) \in R[x]$](../../assets/latex/algebra_92f22474b9af5baaae581bd27764aefbe2b62aff.png) at the matrix
at the matrix 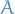 gives zero.
gives zero.
Let

where  denotes the adjugate matrix of
denotes the adjugate matrix of  and
and  .
.
Observe then that

by the propoerty of the adjugate matrix.
Since  is a matrix whose entries are a polynomial, we can write
is a matrix whose entries are a polynomial, we can write  as
as
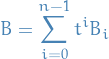
for some matrices  .
.
Therefore,
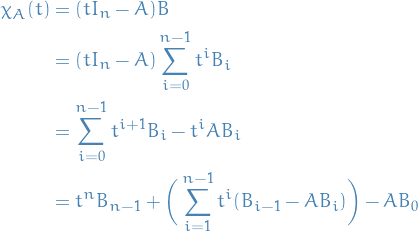
Now, letting

we obtain the following relations
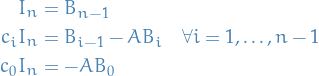
Multiplying the above relations by 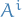 for each
for each  we get the following
we get the following
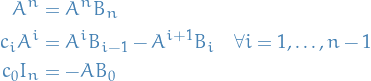
Substituting back into the above series, we have
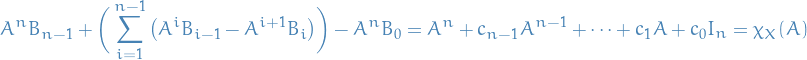
we observe that the LHS vanishes, since we can group terms which cancel! Hence
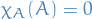
Eigenvalues and Eigenvectors
Theorems
Each endomorphism of non-zero finite dimensional vector space over an algebraically closed field has an eigenvalue.
Inner Product Spaces
Definitions
Inner product
An inner product is a (anti-)bilinear map 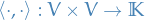 which is
which is
- Symmetric
- Non-degenerate
- Positive-definite
Forms
Let 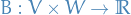 . We say
. We say  is a bilinear form if
is a bilinear form if
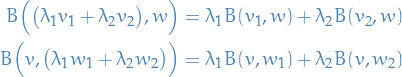
for  ,
,  and
and  .
.
A symmetric bilinear form on  is a bilinear map
is a bilinear map  such that
such that  .
.
Given two 1-forms  at
at  define a symmtric bilinear form
define a symmtric bilinear form  on
on  by
by

where  .
.
Note that  and we denote
and we denote 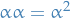 .
.
REDEFINE WITHOUT THE ADDED TANGENT-SPACE STRUCTURE, BUT ONLY USING VECTOR SPACE STRUCTURE.
A symmetric tensor on  is a map which assigns to each
is a map which assigns to each  a symmetric bilinear form on
a symmetric bilinear form on  ; it can be written as
; it can be written as

where 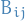 are smooth functions on
are smooth functions on  .
.
Remember, we're using Einstein notation.
Skew-linear and sesquilinear form
We say the mapping  between complex vector spaces is skew-linear if
between complex vector spaces is skew-linear if
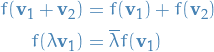
Let  be a vector space over
be a vector space over  equipped with the inner product
equipped with the inner product
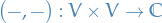
Since this mapping is skew-linear in the second argument, i.e.

we say this is a sesquilinear form.
Hermitian
Theorems
Let  be a vectors in an inner product space. Then
be a vectors in an inner product space. Then

with equailty if and only if  and
and  are linearly dependent.
are linearly dependent.
Adjoints and Self-adjoints
Let  be an inner product space. then two endomorphism
be an inner product space. then two endomorphism  are called adjoint to if the following holds:
are called adjoint to if the following holds:

Let 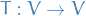 and
and  be the adjoint of
be the adjoint of  . We say
. We say  is self-adjoint if and only if
is self-adjoint if and only if
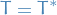
Let  be a finite-dimensional inner product space and let
be a finite-dimensional inner product space and let 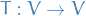 be a self-adjoint linear mapping.
be a self-adjoint linear mapping.
Then  has an orthonormal basis consisting of eigenvectors of
has an orthonormal basis consisting of eigenvectors of  .
.
We'll prove this using induction on  . Let
. Let 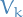 denote the an inner product space with
denote the an inner product space with 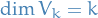 with the self-adjoint linear mapping
with the self-adjoint linear mapping  .
.
Base case: 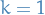 .
Let
.
Let  denote an eigenvector of
denote an eigenvector of  , i.e.
, i.e.
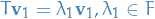
where  is the underlying field of the vector space
is the underlying field of the vector space  . Then clearly
. Then clearly  spans
spans  .
.
General case: Assume the hypothesis holds for  , then
, then

where

Further, let  and
and  with
with  be an eigenvector of
be an eigenvector of  . Then
. Then

since  is self-adjoint. This implies that
is self-adjoint. This implies that
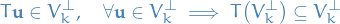
Therefore, restricting  to
to  we have the mapping
we have the mapping

Where  is also self-adjoint, since
is also self-adjoint, since  is self-adjoint on the entirety of
is self-adjoint on the entirety of  . Thus, by assumption, we know that there exists a basis of
. Thus, by assumption, we know that there exists a basis of  consisting of eigenvectors of
consisting of eigenvectors of  , which are therefore orthogonal to the eigenvectors of
, which are therefore orthogonal to the eigenvectors of  in
in 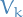 . Hence, existence of basis of eigenvectors for
. Hence, existence of basis of eigenvectors for 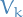 implies existence of basis of eigenvectors of
implies existence of basis of eigenvectors of  .
.
Thus, by the induction hypothesis, if  is a self-adjoint operator on the inner product space
is a self-adjoint operator on the inner product space  with
with  ,
,  , then there exists a basis of eigenvectors of
, then there exists a basis of eigenvectors of  for
for  , as claimed.
, as claimed.
Jordan Normal Form
Notation
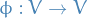 is an endomorphism of the finite dimensional F-vector space
is an endomorphism of the finite dimensional F-vector space  .
.Characteristic equation of
 :
:
![\begin{equation*}
\chi_{\phi}(x) = \big( \lambda_1 - x \big)^{a_1} \big( \lambda_2 - x \big)^{a_2} \cdots \big( \lambda_s - x \big)^{a_s} \in F[x]
\end{equation*}](../../assets/latex/algebra_a6e0c2cd5b6fc3f9ed9dcf6ca50f1e6ef5a8da83.png)

Polynomials
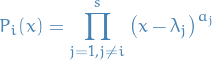
Generalized eigenspace of
 wrt. eigenvalue
wrt. eigenvalue 
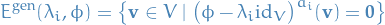
 denotes the dimension of
denotes the dimension of 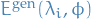
Basis
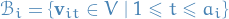
Restriction of


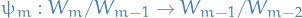 defined
defined

is well-defined and injective.
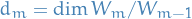
Definitions
An endomorphism  of an F-vector space is called nilpotent if and only if
of an F-vector space is called nilpotent if and only if  such that
such that
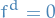
Motivation
 be a finite dimensional vector space
be a finite dimensional vector space an endomorphism
an endomorphism
- a choice of ordered basis
 for
for  determines a matrix
determines a matrix ![$~_{\mathcal{B}} [f]_{\mathcal{B}}$](../../assets/latex/algebra_a0841be11b162a5f21684e66cd4bbb4945c870dc.png) representing
representing  wrt. basis
wrt. basis 
- a choice of ordered basis
- Another choice of basis leads to a different representation; would like to find the simplest possible matrix that is conjugate to a given matrix
Theorem
Given an integer  , we define the
, we define the  matrix
matrix 

or equivalently,
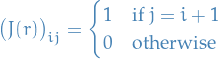
which we call the nilpotent Jordan block of size  .
.
Given an integer  and a scalar
and a scalar  define an
define an  matrix
matrix  as
as
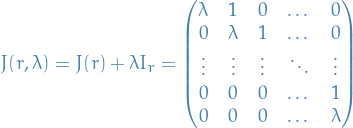
which we is called the Jordan block of size  and eigenvalue
and eigenvalue  .
.
Let  be an algebraically closed field, and
be an algebraically closed field, and  be a finite dimensional vector space and
be a finite dimensional vector space and 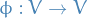 be an endomorphism of
be an endomorphism of  with characteristic polynomial
with characteristic polynomial
![\begin{equation*}
\chi_{\phi}(x) = \big( \lambda_i - x \big)^{a_1} \big( \lambda_2 - x \big)^{a_2} \cdots \big( \lambda_s - x \big)^{a_s} \in F[x]
\end{equation*}](../../assets/latex/algebra_e1a53a69bbd5627923568c535b83662d5601988c.png)
where  and
and  , for distinct
, for distinct  .
.
Then there exists an ordered basis  of
of  s.t.
s.t.
![\begin{equation*}
~_{\mathcal{B}}[\phi]_{\mathcal{B}} = \text{diag} \Big( J(r_{11}, \lambda_1), \dots, J(r_{1 m_1}, \lambda_1), J(r_{21}, \lambda_2), \dots, J(r_{s m_s}, \lambda_s) \Big)
\end{equation*}](../../assets/latex/algebra_05ed2912f98e30105137f8a206da16019fc0403a.png)
with  such that
such that
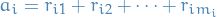
with  .
.
That is,  in the basis
in the basis  is block diagonal with Jordan blocks on the diagonal!
is block diagonal with Jordan blocks on the diagonal!
Proof of Jordan Normal Form
- Outline
We will prove the Jordan Normal form in three main steps:
Decompose the vector space
 into a direct sum
into a direct sum
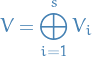
according to the factorization of the characteristic polynomial as a product of linear factors:
![\begin{equation*}
\chi_{\phi}(x) = \big( \lambda_1 - x \big)^{a_1} \big( \lambda_2 - x \big)^{a_2} \cdots \big( \lambda_s - x \big)^{a_s} \in F[x]
\end{equation*}](../../assets/latex/algebra_b54120af1b855bb5c6cd87af6b184bc83bfbdf6c.png)
for distinct scalars
 , where for each
, where for each  :
:
- Focus attention on each of the
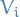 to obtain the nilpotent Jordan blocks.
to obtain the nilpotent Jordan blocks. - Combine Step 2 and 3
- Step 1: Decompose
Rewriting
 as
as
![\begin{equation*}
\chi_{\phi}(x) = (-1)^n \prod_{j = 1}^s \big( x - \lambda_j \big)^{a_j} \in F[x]
\end{equation*}](../../assets/latex/algebra_c4013d57b73134bd93174af5478306011fe6127a.png)
where
 are the eigenvalues of
are the eigenvalues of  .
.
For
 define
define
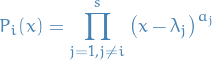
There exists polynomials
![$Q_i(x) \in F[x]$](../../assets/latex/algebra_32c1fc31e99cf3fb193b232e2facf657e1b59eab.png) such that
such that
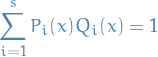
For each
 , let
, let
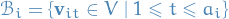
be a basis of
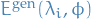 , where
, where  is the algebraic multiplicity of
is the algebraic multiplicity of  with eigenvalue
with eigenvalue  .
.
- Each
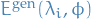 is stable under
is stable under  , i.e.
, i.e. 
For each
 ,
,  such that
such that
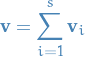
In other words, there is a direct sum decomposition
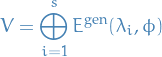
Then

is a basis of
 , so in particular
, so in particular  .
The matrix of the endomorphism
.
The matrix of the endomorphism  wrt. to basis
wrt. to basis  is given by the block diagonal matrix
is given by the block diagonal matrix
![\begin{equation*}
~_{\mathcal{B}}[\phi]_{\mathcal{B}} =
\left(
\begin{array}{c|c|c|c}
B_1 & 0 & 0 & 0 \\
\hline
0 & B_2 & 0 & 0 \\
\hline
0 & 0 & \ddots & 0 \\
\hline
0 & 0 & 0 & B_s
\end{array}
\right)
\in \text{Mat}(n; F)
\end{equation*}](../../assets/latex/algebra_c02066ebcd6aed4e5ad9ad676c504f6743b1c78d.png)
with
![$B_i = ~_{\mathcal{B}}[\phi_i]_{\mathcal{B}} \in \text{Mat}(a_i; F)$](../../assets/latex/algebra_4e8e2a19c239252a2bec5dc9c2e4dd64341dc9da.png) .
.
Let
 is that
is that

Then
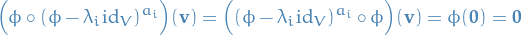
Hence
 , i.e.
, i.e. 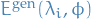 is stable under
is stable under  .
.
By Lemma 6.3.1 we have
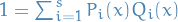 and so evaluating this at
and so evaluating this at  , we get
, we get
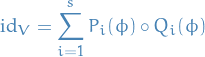
Therefore,
 , we have
, we have

Observe that
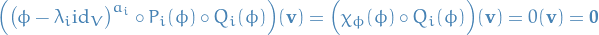
where we've used Cailey-Hamilton Theorem for the second equality. Let

then
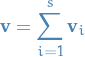
hence all
 can be written as a sum of
can be written as a sum of  , or equivalently,
, or equivalently,
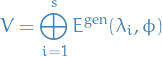
as claimed.
Since
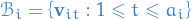 is a basis of
is a basis of 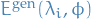 for each
for each  , and since
, and since

we have
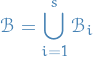
form a basis of
 .
Consider the ordered basis
.
Consider the ordered basis 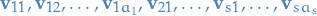 , then the
, then the  can be expressed as a linear combination of the vectors
can be expressed as a linear combination of the vectors  with
with  . Therefore the matrix is block diagonal with i-th block having size
. Therefore the matrix is block diagonal with i-th block having size  .
.
From this, one can prove that any matrix
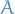 can be written as a Jordan decomposition:
can be written as a Jordan decomposition:
Let
 , then there exists a diagonalisable (NOT diagonal) matrix
, then there exists a diagonalisable (NOT diagonal) matrix  and nilpotent matrix
and nilpotent matrix  such that
such that
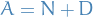
In fact, this decomposition is unique and is called the Jordan decomposition.
- Each
- Step 2: Nilpotent endomorphisms
Let
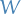 be a finite dimensional vector space and
be a finite dimensional vector space and  such that
such that

for some
 , i.e.
, i.e.  is nilpotent. Further, let
is nilpotent. Further, let  be minimal, i.e.
be minimal, i.e.  but
but 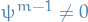 .
.
For
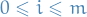 define
define

If
 then
then

i.e.
 , hence
, hence

Moreover, since
 and
and  , we have
, we have 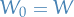 and
and  . Therefore we get the chain of subspaces
. Therefore we get the chain of subspaces

We can now develop an algorithm for constructing a basis!
- Constructing a basis
- Choose arbitrary basis
 for
for 
- Choose basis of
 of
of 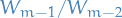 by mapping
by mapping  using
using  and choosing vectors linearly independent of
and choosing vectors linearly independent of  .
. - Repeat!
Or more accurately:
Choose arbitrary basis for
 :
:

Since
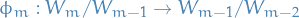 is injective, by the fact that the image of a set of linear independent vectors is a linearly independent set if the map is injective, then
is injective, by the fact that the image of a set of linear independent vectors is a linearly independent set if the map is injective, then

is linearly independent.
Choose vectors
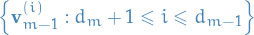
such that
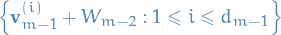
is a basis of
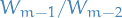 .
.
- Repeat!
Now, the interesting part is this:
Let
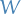 be a finite dimensional vector space and
be a finite dimensional vector space and  such that
such that

for some
 , i.e.
, i.e.  is nilpotent.
is nilpotent.
Let
 be the ordered basis of
be the ordered basis of 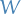 constructed as above
constructed as above

Then
![\begin{equation*}
~_{\mathcal{B}}[\psi]_{\mathcal{B}} = \diag \Big( \underbrace{J(m), \dots, J(m)}_{d_m \text{ times}}, \underbrace{J(m - 1), \dots, J(m - 1)}_{d_{m - 1} - d_m \text{ times}}, \dots, \underbrace{J(1), \dots, J(1)}_{d_1 - d_2 \text{ times}} \Big)
\end{equation*}](../../assets/latex/algebra_4edc751c9e7702a08963fb883685d09e5fca763a.png)
where
 denotes the nilpotent Jordan block of size
denotes the nilpotent Jordan block of size  .
.
It follows from the explicit construction of the basis
 that
that
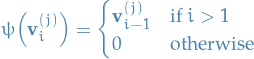
Since
![$~_{\mathcal{B}}[\psi]_{\mathcal{B}}$](../../assets/latex/algebra_709e9b66cf9d42445a73e4468667cefc6dbd2bda.png) is defined by how it maps the basis vectors in
is defined by how it maps the basis vectors in  , and in the basis
, and in the basis 
 becomes a vector of all zeros except the entry corresponding to the j-th basis-vector chosen for
becomes a vector of all zeros except the entry corresponding to the j-th basis-vector chosen for  , where it is a 1.
, where it is a 1.
Hence
![$~_{\mathcal{B}}[\psi]_{\mathcal{B}}$](../../assets/latex/algebra_709e9b66cf9d42445a73e4468667cefc6dbd2bda.png) is a nilpotent Jordan block as claimed.
is a nilpotent Jordan block as claimed.
Concluding step 2; for all nilpotent endomorphisms there exists a basis such that the representing matrix can be written as a block diagonal matrix with nilpotent Jordan blocks along the diagonal.
- Choose arbitrary basis
- Constructing a basis
- Step 3: Bringing it together
Again considering the endomorphisms
 restricted to
restricted to 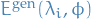 , we can apply Proposition 6.3.9 to see that this endomorphism can be written as a block diagon matrix of the form stated for a suitable choice of basis.
, we can apply Proposition 6.3.9 to see that this endomorphism can be written as a block diagon matrix of the form stated for a suitable choice of basis.
The endomorphism
 restricted to
restricted to 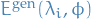 is of course
is of course  , thus the matrix wrt. the chosen basis is just
, thus the matrix wrt. the chosen basis is just  . Therefore the matrix for
. Therefore the matrix for  (when restricted to
(when restricted to 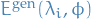 ) is just
) is just  plus
plus  , i.e.
, i.e.  .
.
Thus, each
 appearing in this theorem is exactly of the form we stated in Jordan Normal form.
appearing in this theorem is exactly of the form we stated in Jordan Normal form.
Algorithm
Calculate the eigenvalues,
 of
of 
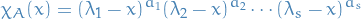
For each
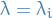 and
and 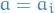 , let
, let

Compute
 and
and
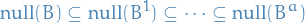
Let

Set
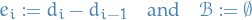
i.e. the difference in dimension between each of the nullspaces.
- Let
 be the largest integer such that
be the largest integer such that  .
. - If
 does not exist, stop.
Otherwise, goto step 3.
does not exist, stop.
Otherwise, goto step 3. - Let
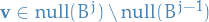 and
and 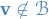 .
. - Let

- Change
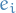 to
to  for
for 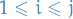 .
.
- Let
- Let the full basis be the union of all the
 , i.e.
, i.e.  .
.
Tensor spaces
The tensor product  between two vector spaces
between two vector spaces 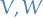 is a vector space with the properties:
is a vector space with the properties:
- if
 and
and  , there is a "product"
, there is a "product" 
This product
 is bilinear:
is bilinear:
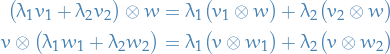
for
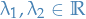 ,
,  and
and  .
.
I find the following instructive to consider.
In the case of a Cartesian product, the vector spaces are still "independent" in the sense that any element can be expressed in the basis
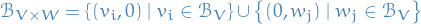
which means

Now, in the case of a tensor product, we in some sense "intertwine" the spaces, making it so that we cannot express elements as "one part from  and one part from
and one part from 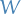 ". And so we need the basis
". And so we need the basis

Therefore
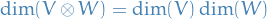
By universal property of tensor products we can instead define the tensor product between two vector spaces 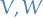 as the dual vector space of bilinear forms on
as the dual vector space of bilinear forms on  .
.
If  ,
,  , then
, then  is defined as the map
is defined as the map

for every bilinear form  .
.
That is,

and

by
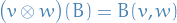
Observe that this satisfies the universal property of tensor product since if we are given some  , for every
, for every  , i.e.
, i.e.  , we have
, we have  , i.e.
, i.e.  is a bilinear form on
is a bilinear form on  . Furthermore, this dual of bilinear forms on
. Furthermore, this dual of bilinear forms on  is then
is then  (since we are working with finite-dimensional vector spaces).
(since we are working with finite-dimensional vector spaces).

From universal property of tensor product, for any  , there exists a unique
, there exists a unique 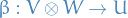 such that
such that

Letting the map

be defined by

where  is defined by
is defined by  . By the uniqueness of
. By the uniqueness of  , and linearity of the maps under consideration, this defines an isomorphism between the spaces.
, and linearity of the maps under consideration, this defines an isomorphism between the spaces.
Suppose
 is a basis for
is a basis for 
 is a basis for
is a basis for 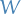
Then a bilinear form 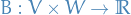 is fully defined by
is fully defined by  (upper-indices since these are the coefficients of the co-vectors). Therefore,
(upper-indices since these are the coefficients of the co-vectors). Therefore,

Since we are in finite dimensional vector spaces, the dual space  then has dimension
then has dimension

as well.
Furthermore,  form a basis for
form a basis for  . Therefore we can write the elements in
. Therefore we can write the elements in  as
as


First observe that if  , then
, then  is fully defined by how it maps the basis elements
is fully defined by how it maps the basis elements  , and
, and

Then observe that if  , then
, then
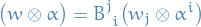
Hence, we have a natural homomorphism which simply takes  , with coefficients
, with coefficients  to the corresponding element
to the corresponding element  with the same coefficients! That is, the isomorphism is given by
with the same coefficients! That is, the isomorphism is given by

Tensor algebra
Now we'll consider letting 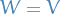 . We define tensor powers as
. We define tensor powers as

with  ,
,  , etc.
We can think of
, etc.
We can think of  as the dual vector space of k-multilinear forms on
as the dual vector space of k-multilinear forms on  .
.
Combining all tensor powers using the direct sum we have define the tensor algebra
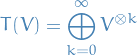
whose elements are finite sums
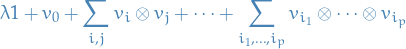
of tensor products of vectors  .
.
The "multiplication" in  is defined by extending linearly the basic product
is defined by extending linearly the basic product

The resulting algebra  is associative, but not commutative.
is associative, but not commutative.
Two viewpoints
There are mainly due two useful ways of looking at tensors:
Using Lemma lemma:homomorphisms-isomorphic-to-1-1-tensor-product, we may view
 tensors as linear maps
tensors as linear maps  . In other words,
. In other words,

- Furthermore, we can view
 as the dual of
as the dual of  , i.e. consider a
, i.e. consider a 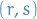 tensor as a "multilinear machine" which takes in
tensor as a "multilinear machine" which takes in  vectors and
vectors and  co-vectors, and spits out a real number!
co-vectors, and spits out a real number!
- Furthermore, we can view
- By explicitly considering bases
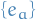 of
of  and
and  of
of  , the
, the 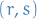 tensors are fully defined by how they map each combination of the basis elements. Therefore we can view tensors as multi-dimensional arrays!
tensors are fully defined by how they map each combination of the basis elements. Therefore we can view tensors as multi-dimensional arrays!
Tensors (mainly as multidimensional arrays)
Let  be a vector space
be a vector space  where
where  is some field,
is some field,  is addition in the vector space and
is addition in the vector space and  is scalar-multiplication.
is scalar-multiplication.
Then a tensor  is simply a linear map from some q-th Cartesian product of the dual space
is simply a linear map from some q-th Cartesian product of the dual space  and some p-th Cartesian product of the vector space
and some p-th Cartesian product of the vector space  to the reals
to the reals  . In short:
. In short:
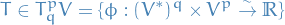
where 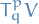 denotes the (p, q) tensor-space on the vector space
denotes the (p, q) tensor-space on the vector space  , i.e. linear maps from Cartesian products of the vector space and it's dual space to a real number.
, i.e. linear maps from Cartesian products of the vector space and it's dual space to a real number.
Tensors are geometric objects which describe linear relations between geometric vectors, scalars, and other tensors.
A tensor of type 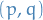 is an assignment of a multidimensional array
is an assignment of a multidimensional array
![\begin{equation*}
T_{j_1, \dots, j_q}^{i_1, \dots, i_p} [ \mathbf{f} ]
\end{equation*}](../../assets/latex/algebra_4636b2bb9b5133c787efc5f0063b4b8d040bc734.png)
to each basis 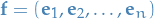 of an n-dimensional vector space such that, if we apply the change of basis
of an n-dimensional vector space such that, if we apply the change of basis

Then the multi-dimensional array obeys the transformation law
![\begin{equation*}
T_{j'_1 \dots, j'_p}^{i'_1, \dots, i'_q} [\mathbf{f} \cdot R] = \big( R^{-1} \big)_{i_1}^{i'_1} \dots \big( R^{-1} \big)_{i_p}^{i'_p} \
T_{j_1, \dots, j_q}^{i_1, \dots, i_p} [ \mathbf{f} ] \
R_{j'_1}^{j_1} \dots R_{j'_q}^{j_q}
\end{equation*}](../../assets/latex/algebra_db97bd8ea12841f1c2aac31a4c97d6146d2cfe89.png)
We say the order of a tensor is  if we require an n-dimensional array to describe the relation the tensor defines between the vector spaces.
if we require an n-dimensional array to describe the relation the tensor defines between the vector spaces.
Tensors are classified according to the number of contra-variant and co-variant indices, using the notation 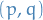 , where
, where
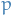 is # of contra-variant indices
is # of contra-variant indices is # of co-variant indices
is # of co-variant indices
Examples:
- Scalar :
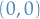
- Vector :
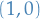
- Matrix :
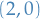
- 1-form:
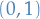
- Symmetric bilinear form:
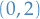
The tensor product takes two tensors,  and
and  , and produces a new tensor,
, and produces a new tensor,  , whose order is the sum of the orders of the original tensors.
, whose order is the sum of the orders of the original tensors.
When described as multilinear maps, the tensor product simply multiplies the two tensors, i.e.
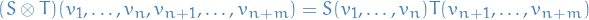
which again produces a map that is linear in its arguments.
On the components, this corresponds to multply the components of the two input tensors pairwise, i.e.
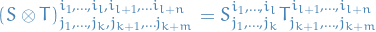
where
 is of type
is of type 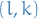
 is of type
is of type 
Then the tensor product  is of type
is of type 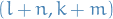 .
.
Let 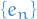 be a basis of the vector space
be a basis of the vector space  with
with  , and
, and  be the basis of
be the basis of  .
.
Then  is a basis for the vector space of
is a basis for the vector space of  over
over  , and so
, and so

Given 
 , we define
, we define 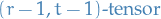


Components:

A contraction is basis independent:
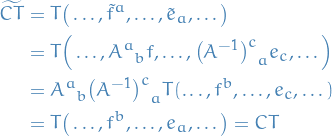
![\begin{equation*}
\begin{split}
\tensor{T}{_{(a, b)}} &= \frac{1}{2} \big( \tensor{T}{_{ab}} + T_{ba} \big) \implies T_{(a, b)} = T_{(b, a)} \\
\tensor{T}{_{[a, b]}} &= \frac{1}{2} \big( \tensor{T}{_{ab}} - \tensor{T}{_{ba}} \big) \implies T_{[a, b]} = - T_{[b, a]}
\end{split}
\end{equation*}](../../assets/latex/algebra_b9131aa9bf3922b3d3c0d9cbcef308cfd5df2086.png)
Generalized to  by summing over combinations of the indices, alternating sign if wanting anti-symmetric. See the general definition of a wedge product for more for example.
by summing over combinations of the indices, alternating sign if wanting anti-symmetric. See the general definition of a wedge product for more for example.
Clifford algebra
First we need the following definition:
Given a commutative ring  and
and  modules M$ and
modules M$ and  , an
, an  quadratic function
quadratic function 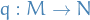 s.t.
s.t.
(cube relation): For any
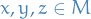 we have
we have

(homegenous of degree 2): For any
 and any
and any  , we have
, we have
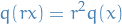
A quadratic R-module is an  module
module  equipped with a quadratic form: an R-quadratic function on
equipped with a quadratic form: an R-quadratic function on  with values in
with values in  .
.
The Clifford algebra  of a quadratic R-module
of a quadratic R-module 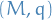 can be defined as the quotient of the tensor algebra
can be defined as the quotient of the tensor algebra 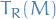 by the ideal generated by the relations
by the ideal generated by the relations  for all
for all  ; that is
; that is

where  is the ideal generated by
is the ideal generated by  .
.
In the case we're working with a vector space  (instead of a module), we have
(instead of a module), we have

Since the tensor algebra  is naturally
is naturally  graded, the Clifford algebra
graded, the Clifford algebra  is naturally
is naturally 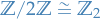 graded.
graded.
Examples
Exterior / Grassman algebra
Consider a Clifford algebra
 generated by the quadratic form
generated by the quadratic form
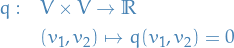
i.e. identically zero.
- This apparently gives you the Exterior algebra over

- A bit confused as to why
 .
.


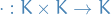
 over a set
over a set 




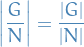
![$P, Q \in R[x]$](../../assets/latex/algebra_fa38ebe1290060ad090d58f4eb95b6cc97a96984.png) with
with ![$A, B \in R[X]$](../../assets/latex/algebra_8de73281313189b1e708a2e79052789e62370129.png) such that
such that

 or
or 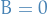 .
.






 is symmetric, i.e.
is symmetric, i.e.

 is a Hermitian.
is a Hermitian.

 be a
be a 