Probability & Statistics
Table of Contents
Notation
 denotes the distribution of some random variable
denotes the distribution of some random variable 
 means convergence in probability for random elements
means convergence in probability for random elements  , refers to
, refers to

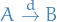 means convergence in distribution for random elements
means convergence in distribution for random elements  , i.e.
, i.e. 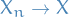 in distribution if
in distribution if  for all continuity points
for all continuity points  of
of  .
. means almost surely convergence for random elements
means almost surely convergence for random elements 
Theorems
Chebyshev Inequality
Let  (integrable) be a random variable with finite expected value
(integrable) be a random variable with finite expected value  and finite non-zero variance
and finite non-zero variance 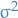 .
.
Then for any real number  ,
,

Let  be a measure space, and let
be a measure space, and let  be an extended real-valued measureable-function defined on
be an extended real-valued measureable-function defined on  .
.
Then for any real number  and
and 

Or more generally, if  is an extended real-valued measurable function, nonnegative and nondecreasing on the range of
is an extended real-valued measurable function, nonnegative and nondecreasing on the range of  , then
, then

Hmm, not quite sure how to relate the probabilistic and measure-theoretic definition..
Markov Inequality
If  is a nonnegative random variable and
is a nonnegative random variable and  , then
, then
![\begin{equation*}
P \big( X \ge a \big) \le \frac{\mathbb{E}[X]}{a}
\end{equation*}](../../assets/latex/probability_and_statistics_019a98278452845f8b8bb6b44608297d85c8e1a4.png)
First note that
![\begin{equation*}
\mathbb{E}[X] = \int_{0}^{\infty} \mathbb{P}(X \ge t) \dd{t}
\end{equation*}](../../assets/latex/probability_and_statistics_8c1c901415a27fd332fa45ee2e8acb4dbb3c486c.png)
and
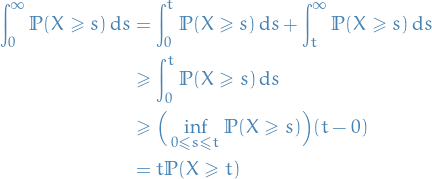
Hence,
![\begin{equation*}
\mathbb{P}(X \ge t) \le \frac{\mathbb{E}[X]}{t}
\end{equation*}](../../assets/latex/probability_and_statistics_fe338901aa40dfd0b5f0c6f1454f4a90f05dc8b9.png)
Law of large numbers
There are mainly two laws of large numbers:
Often the assumption of finite variance is made, but this is in fact not necessary (but makes the proof easier). Large or infinite variance will make the convergence slower, but the Law of Large Numbers holds anyway.
Central Limit Theorem
Suppose  is a sequence of i.i.d. random variables with
is a sequence of i.i.d. random variables with ![$\mathbb{E}[X_i] = \mu$](../../assets/latex/probability_and_statistics_49407bea91d8d9a9fb1131a9ad1c70aa646f9c12.png) and
and  . Then,
. Then,
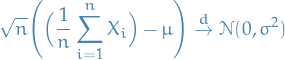
where  means convergence in distribution, i.e. that the cumulative distribution functions of
means convergence in distribution, i.e. that the cumulative distribution functions of  converge pointwise to the cdf of the
converge pointwise to the cdf of the 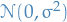 distribution: for any real number
distribution: for any real number  ,
,
![\begin{equation*}
\underset{n \to \infty}{\lim} \Pr [ \sqrt{n} (S_n - \mu) \le z ] = \Phi \Big( \frac{z}{\sigma} \Big)
\end{equation*}](../../assets/latex/probability_and_statistics_93e25db4d6b2ee1fdff8306810f893dd273d7c21.png)
Jensen's Inequality
If
 is a convex function.
is a convex function. is a rv.
is a rv.
Then ![$f(E[X]) \leq E[f(x)]$](../../assets/latex/probability_and_statistics_5a704c191584b112ce2eae76d3f11effcc23f4d9.png) .
.
Further, if  (
( is strictly convex), then
is strictly convex), then
![$E[(f(X)] = f(E[X]) \iff X = E[X]$](../../assets/latex/probability_and_statistics_1a19363be0c70d388d505c858c79d669d8e4944c.png) "with probability 1".
"with probability 1".
If we instead have:
 is a concave function
is a concave function
Then ![$f(E[X]) \geq E[f(X)]$](../../assets/latex/probability_and_statistics_e3025aae464d32e3c1aa1104a8897f1d7c98b121.png) . This is the one we need for the derivation of EM-algorithm.
. This is the one we need for the derivation of EM-algorithm.
To get a visual intuition, here is a image from Wikipedia:

Continuous Mapping Theorem
Let  ,
,  be random elements defined on a metric space
be random elements defined on a metric space  .
.
Suppose a function  (where
(where  is another metric space) has the set of discountinuity points
is another metric space) has the set of discountinuity points 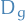 such that
such that  .
.
Then,
We start with convergence in distribution, for which we will need a particular statement from the
Slutsky's Lemma
Let  ,
,  be sequences of scalarvectormatrix random elements.
be sequences of scalarvectormatrix random elements.
If  and
and  , where
, where  is a constant, then
is a constant, then
This follows from the fact that if:

then the joint vector  converges in distribution to
converges in distribution to 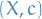 , i.e.
, i.e.
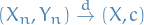
Next we simply apply the Continuous Mapping Theorem, recognizing the functions
as continuous (for the last mapping to be continuous, 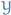 has to invertible).
has to invertible).
Definitions
Probability space
A probability space is a measure space 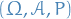 such that the measure of the whole space is equal to one, i.e.
such that the measure of the whole space is equal to one, i.e.
 is the sample space (some arbitrary non-empty set)
is the sample space (some arbitrary non-empty set) is the σ-algebra over
is the σ-algebra over  , which is the set of possible events
, which is the set of possible events![$P: \mathcal{A} \to [0, 1]$](../../assets/latex/probability_and_statistics_f7513392d4fb753f764bd899e9b66b18ef63e836.png) which is the probability measure such that
which is the probability measure such that
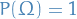
Random measure
Let  be a separable metric space (e.g.
be a separable metric space (e.g.  ) and let
) and let  be its Borel σ-algebra.
be its Borel σ-algebra.
 is a transition kernel from a probability space
is a transition kernel from a probability space 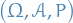 to
to  if
if
For any fixed
 , the mapping
, the mapping

is a measurable function from
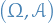 to
to 
For every fixed
 , the mapping
, the mapping
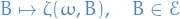
is a (often, probability) measure on

We say a transition kernel is locally finite, if

satisfy  for all bounded measurable sets
for all bounded measurable sets  and for all
and for all  except for some zero-measure set (under
except for some zero-measure set (under  ).
).
Let  be a separable metric space (e.g.
be a separable metric space (e.g. 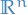 ) and let
) and let 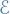 be its Borel σ-algebra.
be its Borel σ-algebra.
A random measure  is a (a.s.) /locally finite transition kernel from a (abstract) probability space
is a (a.s.) /locally finite transition kernel from a (abstract) probability space 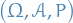 to
to  .
.
Let  be a random measure on the measurable space
be a random measure on the measurable space 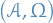 and denote the expected value of a random element
and denote the expected value of a random element  with
with ![$\mathbb{E}[Y]$](../../assets/latex/probability_and_statistics_9e0e384984976b658d0d13ce54607cbf71b8971c.png) .
.
The intensity measure  is defined
is defined
![\begin{equation*}
\begin{split}
\mathbb{E}\zeta: \quad & \mathcal{A} \to [0, \infty] \\
& A \mapsto \mathbb{E}\zeta(A) := \mathbb{E} \big[ \zeta(A) \big], \quad \forall A \in \mathcal{A}
\end{split}
\end{equation*}](../../assets/latex/probability_and_statistics_5e3283180c137582df4df73bf4f0e9d976dd4389.png)
So it's a non-random measure which sends an element 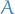 of the sigma-algebra
of the sigma-algebra  to the expected value of the
to the expected value of the  , since
, since  is a measurable function, i.e. a random variable.
is a measurable function, i.e. a random variable.
Poisson process
A Poisson process is a generalized notion of a Poisson random variable.
A point process  is a (general) Poisson process with intensity
is a (general) Poisson process with intensity  if it has the two following properties:
if it has the two following properties:
- Number of points in a bounded Borel set
 is a Poisson random variable with mean
is a Poisson random variable with mean  .
.
In other words, denote the total number of points located in
 by
by  , then the probability of random variable
, then the probability of random variable  being equal to
being equal to  is given by
is given by
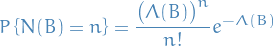
- Number of points in
 disjoint Borel sets form
disjoint Borel sets form  independent random variables.
independent random variables.
The Radon measure  maintains its previous interpretation of being the expected number of points
maintains its previous interpretation of being the expected number of points  located in the bounded region
located in the bounded region  , namely
, namely
![\begin{equation*}
\Lambda(B) = \mathbb{E} \big[ N(B) \big]
\end{equation*}](../../assets/latex/probability_and_statistics_bf9b7cb287260c314f383ac0bf30d6631f3b9b4b.png)
Cox process
Let  be a random measure.
be a random measure.
A random measure  is called a Cox process directed by
is called a Cox process directed by  , if
, if  is a Poisson process with intensity measure
is a Poisson process with intensity measure  .
.
Here  is the conditional distribution of
is the conditional distribution of  , given
, given  .
.
Degeneracy of probability distributions
A degenerate probability distribution is a probability distribution with support only on a lower-dimensional space.
E.g. if the degenerate distribution is univariate (invoving a single random variable), then it's a deterministic distribution, only taking on a single value.
Characteristic function
Let  be a random variable with density
be a random variable with density  and cumulative distribution function
and cumulative distribution function  .
.
Then the characteristic equation is defined as the Fourier transform of  :
:
![\begin{equation*}
\begin{split}
\varphi_X(t) &= \mathbb{E} \big[ e^{i t X} \big] \\
&= \int_{\mathbb{R}}^{} e^{i t x} \dd{F_X(x)} \\
&= \int_{\mathbb{R}}^{} e^{i t x} f(x) \ \dd{x} \\
&= \mathcal{F} \left\{ f(x) \right\}
\end{split}
\end{equation*}](../../assets/latex/probability_and_statistics_0ae57b2266ee55fcc78f2b1e6a84e6daaceda032.png)
Examples
10 dice: you want at least one 4, one 3, one 2, one 1
Consider the number of misses before a first "hit". When we say "hit", we refer to throwing something in the set 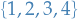 .
.
Then we can do as follows:
 is the # of misses before our first "hit"
is the # of misses before our first "hit" is the # of misses between our first "hit" and second "hit"
is the # of misses between our first "hit" and second "hit"- …
We then observe the following:
 since if we have more than
since if we have more than  misses before our first hit, we'll never be able to get all the events in our target set
misses before our first hit, we'll never be able to get all the events in our target set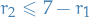


We also observe that there are  ,
,  ,
,  and
and  ways of missing for each of the respective target events.
ways of missing for each of the respective target events.
from sympy import * r_1, r_2, r_3, r_4 = symbols("r_1 r_2 r_3 r_4", nonnegative=True, integers=True) s = Sum( Sum( Sum( Sum( (2**(r_1 - 1) * 3**(r_2 - 1) * 4**(r_3 - 1) * 5**(r_4 - 1)) \ / 6**(r_1 + r_2 + r_3 + r_4), (r_4, 1, 10 - r_1 - r_2 - r_3) ), (r_3, 1, 9 - r_1 - r_2) ), (r_2, 1, 8 - r_1) ), (r_1, 1, 7) ) res = factorial(4) * s.doit() print(res.evalf())
Probability "metrics" / divergences
Notation
Overview of the "metrics" / divergences
These definitions are taken from arjovsky17_wasser_gan
The Total Variation (TV) distance

Or, using slightly different notation, the total variation between two probability measures  and
and  is given by
is given by
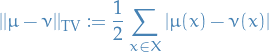
These two notions are completely equivalent. One can see this by observing that any discrepancy between  and
and  is "accounted for twice", since
is "accounted for twice", since 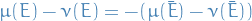 , which is why we get the factor of
, which is why we get the factor of  in front. We can then gather all
in front. We can then gather all  where
where  into a subset
into a subset  , making sure to choose
, making sure to choose  or it's complement
or it's complement  such that the difference is positive when
such that the difference is positive when  in the first term. Then we end up with the
in the first term. Then we end up with the  seen above.
seen above.
The Jensen-Shannon (JS) divergence

where  is the mixture
is the mixture  .
.
This divergence is symmetrical and always defiend because we can choose  .
.
The Earth-Mover (EM) distance or Wasserstein-1
![\begin{equation*}
W(\mathbb{P}_r, \mathbb{P}_g) = \inf_{\gamma \in \Pi(\mathbb{P}_r, \mathbb{P}_g)} \mathbb{E}_{(x, y) \sim \gamma} \big[ \norm{x - y} \big]
\end{equation*}](../../assets/latex/probability_and_statistics_4dc254a423d055e723e06f3b67d8f610b955f76c.png)
where 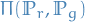 denotes the set of all joint distributions
denotes the set of all joint distributions  whose marginals are respectively
whose marginals are respectively 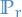 and
and 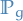 .
.
Intuitively,  indicates how much "mass" must be transported from
indicates how much "mass" must be transported from  to
to 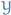 in order to transform the distributions
in order to transform the distributions 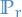 into the distribution
into the distribution 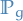 . The EM distance then is the "cost" of the optimal transport plan.
. The EM distance then is the "cost" of the optimal transport plan.
Kullback-Leibler divergence
Definition
The Kullback-Leibler (KL) divergence

where both 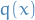 and
and 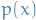 are assumed to be absolutely continuous, and therefore admit densities, wrt. to the same measure
are assumed to be absolutely continuous, and therefore admit densities, wrt. to the same measure  defined on
defined on  .
.
The KL divergence is famously asymmetric and possibly infinite / undefined when there are points s.t.  and
and 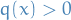 .
.

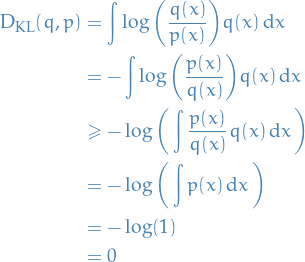
where in the inequality we have use Jensen's inequality together with the fact that  is a convex function.
is a convex function.
Why?
Kullback-Leibner divergence from some probability-distributions  and
and  , denoted
, denoted  ,
is a measure of the information gained when one revises one's beliefs from the prior distribution
,
is a measure of the information gained when one revises one's beliefs from the prior distribution
 to the posterior distribution
to the posterior distribution  . In other words, amount of information lost when
. In other words, amount of information lost when  is used to approximate
is used to approximate  .
.
Most importantly, the KL-divergence can be written
![\begin{equation*}
D_{\rm{KL}}(p \ || \ q) = \mathbb{E}_p\Bigg[\log \frac{p(x \mid \theta^*)}{q(x \mid \theta)} \Bigg] = \mathbb{E}_p \big[ \log p(x \mid \theta^*) \big] - \mathbb{E}_p \big[ \log q(x \mid \theta) \big]
\end{equation*}](../../assets/latex/probability_and_statistics_bf4cacc304ab57b5792eb66e803c948e203e94f0.png)
where  is the optimal parameter and
is the optimal parameter and  is the one we vary to approximate
is the one we vary to approximate 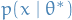 . The second term in the equation above is the only one which depend on the "unknown" parameter
. The second term in the equation above is the only one which depend on the "unknown" parameter  (
( is fixed, since this is the parameter we assume
is fixed, since this is the parameter we assume 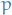 to take on). Now, suppose we have
to take on). Now, suppose we have  samples
samples  from
from 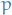 , then observe that the negative log-likelihood for some parametrizable distribution
, then observe that the negative log-likelihood for some parametrizable distribution  is given by
is given by

By the Law of Large numbers, we have
![\begin{equation*}
\lim_{N \to \infty} - \frac{1}{N} \sum_{i=1}^{N} \log q(x_i \mid \theta) = - \mathbb{E}_p[\log q(x \mid \theta)]
\end{equation*}](../../assets/latex/probability_and_statistics_96e04ce0e8b58d7c798481548bd91823470368e0.png)
where  denotes the expectation over the probability density
denotes the expectation over the probability density 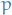 . But this is exactly the second term in the KL-divergence! Hence, minimizing the KL-divergence between
. But this is exactly the second term in the KL-divergence! Hence, minimizing the KL-divergence between 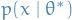 and
and 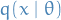 is equivalent of minimizing the negative log-likeliood, or equivalently, maximizing the likelihood!
is equivalent of minimizing the negative log-likeliood, or equivalently, maximizing the likelihood!
Wasserstein metric
Let  be a metric space for which every probability measure on
be a metric space for which every probability measure on 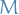 is a Radon measure.
is a Radon measure.
For  , let
, let  denote the collection of all probability measures
denote the collection of all probability measures  on
on 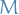 with finite p-th moment (expectation of rv. to the p-th power) for some
with finite p-th moment (expectation of rv. to the p-th power) for some  ,
,

Then the p-th Wasserstein distance between two probability measures  and
and  in
in  is defined as
is defined as
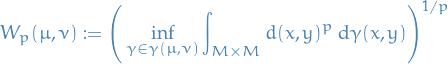
where  denotes the collection of all measures on
denotes the collection of all measures on  with marginals
with marginals  and
and  on the first and second factors respectively (i.e. all possible "joint distributions").
on the first and second factors respectively (i.e. all possible "joint distributions").
Or equivalently,
![\begin{equation*}
W_p(\mu, \nu)^p = \inf \mathbb{E} \big[ d(X, Y)^p \big]
\end{equation*}](../../assets/latex/probability_and_statistics_eff0640986bca7f4d56bdce5777eadd3e5f24976.png)
Intuitively, if each distribution is viewed as a unit amount of "dirt" piled on the metric space 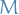 , the metric minimum "cost" of turning one pile into the other, which is assumed to eb the amount dirt that needs to moved times the distance it has to be moved.
, the metric minimum "cost" of turning one pile into the other, which is assumed to eb the amount dirt that needs to moved times the distance it has to be moved.
Because of this analogy, the metric is sometimes known as the "earth mover's distance".
Using the dual representation of 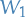 , when
, when  and
and  have bounded support:
have bounded support:
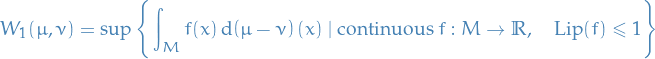
where  denotes the minimal Lipschitz constant for
denotes the minimal Lipschitz constant for  .
.
Compare this with the definition of the Radon metric (metric induced by distance between two measures):
![\begin{equation*}
\rho(\mu, \nu) := \sup \Bigg\{ \int_M f(x) \dd(\mu - \nu)(x) \mid \text{continuous } f: M \to [-1, 1] \Bigg\}
\end{equation*}](../../assets/latex/probability_and_statistics_4496867e36c7eb7a37a1a4f07a2561baefb11961.png)
If the metric  is bounded by some constant
is bounded by some constant  , then
, then

and so convergence in the Radon metric implies convergence in the Wasserstein metric, but not vice versa.
Observe that we can write the duality as
![\begin{equation*}
\begin{split}
W_1(\mu, \nu) &= \sup_{\norm{f}_L \le 1} \int_M f(x) \dd (\mu - \nu)(x) \\
&= \sup_{\norm{f}_L \le 1} \int_M f(x) \dd \mu - \int_M f(x) \dd \nu \\
&= \sup_{\norm{f}_L \le 1} \Big( \mathbb{E}_{x \sim \mu(x)} \big[ f(x) \big] - \mathbb{E}_{x \sim \nu(x)} \big[ f(x) \big] \Big)
\end{split}
\end{equation*}](../../assets/latex/probability_and_statistics_15553e9aefcfe1dedcc8397433ee45e41b303211.png)
where we let 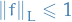 denotes that we're finding the supremum over all functions which are 1-Lipschitz, i.e. Lipschitz continuous with Lipschitz constant 1.
denotes that we're finding the supremum over all functions which are 1-Lipschitz, i.e. Lipschitz continuous with Lipschitz constant 1.
Integral Probability Metric
Let  and
and  be a probablity distributions, and
be a probablity distributions, and  be some space of real-valued functions. Further, let
be some space of real-valued functions. Further, let
![\begin{equation*}
d_{\mathcal{H}}(q, p) = \sup_{h \in \mathcal{H}} \Big[ \mathbb{E}_q [h(X)] - \mathbb{E}_p[h(Z)] \Big]
\end{equation*}](../../assets/latex/probability_and_statistics_0c6c78693beb9e0630c1502d0c10caca561a8c31.png)
When  is sufficently "large", then
is sufficently "large", then

We then say that  together with
together with  defines an integral probabilty metric (IPM).
defines an integral probabilty metric (IPM).
ϕ-divergences
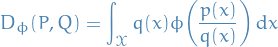
Stein's method
Absolutely fantastic description of it: https://statweb.stanford.edu/~souravc/beam-icm-trans.pdf
Notation
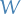 any random variable
any random variable std. Gaussian random variable
std. Gaussian random variable
Overview
- Technique for proving generalized central limit theorems
Ordinary central limit theorem: if
 are i.i.d. rvs. then
are i.i.d. rvs. then
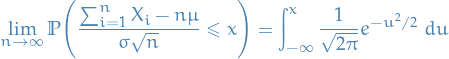
where
 and
and 
- Usual method of proof:
- LHS is computed using Fourier Transform
- Independence implies that FT decomposes as a product
- Analysis
- Stein's motivation: what if
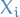 are not exactly independent?!
are not exactly independent?!
Method
Suppose we want to show that 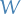 is "approximately Gaussian", i.e.
is "approximately Gaussian", i.e.
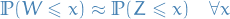
or,
![\begin{equation*}
\mathbb{E}[h(W)] \approx \mathbb{E}[h(Z)]
\end{equation*}](../../assets/latex/probability_and_statistics_06ba62cf66ccd8f2d07b4e7af4c372d3006f9c65.png)
for any well-behaved 
It's a generalization because if
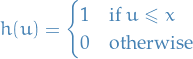
then
![\begin{equation*}
\mathbb{P}(W \le x) = \mathbb{E}[h(W)]
\end{equation*}](../../assets/latex/probability_and_statistics_4b3f596ed4f34ba8748fa9f9529443e4336722a6.png)
Suppose
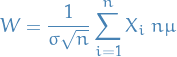
and we want to show that the rv.  is approximately std. Gaussian, i.e.
is approximately std. Gaussian, i.e. ![$\mathbb{E}[h(W)] \approx \mathbb{E}[h(Z)$](../../assets/latex/probability_and_statistics_519176343a58bbe82f34d8418f7478264192526c.png) for all well-behaved
for all well-behaved  .
.
Given
 , obtain a function
, obtain a function  by solving the differential equation
by solving the differential equation
![\begin{equation*}
f'(x) - x f(x) = h(x) - \mathbb{E}[h(z)]
\end{equation*}](../../assets/latex/probability_and_statistics_08424e2fe22e1ee741c245c231dd7f9855374942.png)
2.Show that
![\begin{equation*}
\mathbb{E} \big( f'(W) - W f(W) \big) = \mathbb{E}[h(W)] - \mathbb{E}[h(Z)]
\end{equation*}](../../assets/latex/probability_and_statistics_ed612add542dfee721c1920259327eff80b35f05.png)
using the properties of 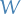
Since
![\begin{equation*}
\mathbb{E} \big( f'(W) - W f(W) \big) = \mathbb{E}[h(W)] - \mathbb{E}[h(Z)
\end{equation*}](../../assets/latex/probability_and_statistics_352fb025d181c9a4a0af1ba900d2354c4280269b.png)
conclude that
![$\mathbb{E}[h(W)] \approx \mathbb{E}[h(Z)]$](../../assets/latex/probability_and_statistics_d41733f6a99a480b597c447684432a841ad974c5.png) .
.
More generally, two smooth densities 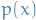 and
and 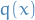 supported on
supported on  are indentical if and only if
are indentical if and only if
![\begin{equation*}
\mathbb{E}_p [\mathbf{s}_p(x) f(x) + \nabla_x f(x) ] = 0
\end{equation*}](../../assets/latex/probability_and_statistics_21eabfd0a3a9afee8f36fed3fff6a71b11356427.png)
for smooth functions  with proper zero-boundary conditions, where
with proper zero-boundary conditions, where

is called the Stein score function of 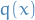 .
.
Stein discrepancy measure between two continuous densities 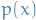 and
and 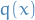 is defined
is defined
![\begin{equation*}
\mathbb{S}(p, q) = \max_{f \in \mathcal{F}} \big( \mathbb{E}_p [ \mathbf{s}_q(x) f(x) + \nabla_x f(x)] \big)^2
\end{equation*}](../../assets/latex/probability_and_statistics_f88b77c8cb9a1b198313c15cbf27b3e14a1ef50c.png)
where  is the set of functions which satisfies
is the set of functions which satisfies
Two smooth densities 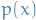 and
and 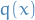 supported on
supported on  are indentical if and only if
are indentical if and only if
![\begin{equation*}
\mathbb{E}_p [\mathbf{s}_q(x) f(x) + \nabla_x f(x) ] = 0
\end{equation*}](../../assets/latex/probability_and_statistics_bc24722f15cc69291023190e774861f5f083e897.png)
for smooth functions  with proper zero-boundary conditions, where
with proper zero-boundary conditions, where

is called the Stein score function of 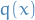 .
.
Stein discrepancy measure between two continuous densities 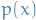 and
and 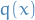 is defined
is defined
![\begin{equation*}
\mathbb{S}(p, q) = \max_{f \in \mathcal{F}} \big( \mathbb{E}_p [ \mathbf{s}_q(x) f(x) + \nabla_x f(x)] \big)^2
\end{equation*}](../../assets/latex/probability_and_statistics_f88b77c8cb9a1b198313c15cbf27b3e14a1ef50c.png)
where  is the set of functions which previous expectation and is also "rich" enough to ensure that
is the set of functions which previous expectation and is also "rich" enough to ensure that 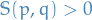 whenever
whenever 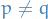 .
.
Why does it work?
- Turns out that if we replace the
![$\mathbb{E}[h(Z)]$](../../assets/latex/probability_and_statistics_94d7d167dd4ca6ec844eb249c4e3e3b5f0be774c.png) in Stein's method, then
in Stein's method, then  is not well-behaved; it blows up at infinity.
is not well-behaved; it blows up at infinity. - A random variable
 has the standard Gaussian distribution if and only if
has the standard Gaussian distribution if and only if  for all
for all  !
(you can easilty check this by observing that the solution to this is
!
(you can easilty check this by observing that the solution to this is  ).
). Differential operator
 , defined as
, defined as
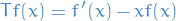
is called a characterizing operator for the standard Gaussian distribution.
Stochastic processes
Discrete
- Markov chains is an example of a discrete stochastic process
Simple random walk
Let  be a set of i.i.d. random variables such that
be a set of i.i.d. random variables such that
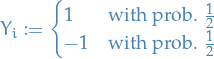
Then, let

We then call the sequence 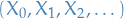 a simple random walk.
a simple random walk.
For large  , due to CLT we have
, due to CLT we have

i.e.  follows a normal distribution with
follows a normal distribution with ![$\mathbb{E}[X_t] = 0$](../../assets/latex/probability_and_statistics_d3e8c75430646506718908bbc841c0b1bb0b8eef.png) and
and 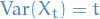 .
.
We then have the following properties:
![$\mathbb{E}[X] = 0$](../../assets/latex/probability_and_statistics_56be98dff9b0eedfc7b4bba0860fc3638ddd82e1.png)
Independent measurements : if
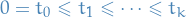
then
 are mutually independent, with
are mutually independent, with  .
.
- Stationary : for all
 and
and  , the distribution of
, the distribution of 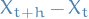 is the same as the distribution of
is the same as the distribution of  .
.
Martingale
A martingale is a stochastic process which is fair game.
We say a stochastic process 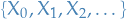 is a martingale if
is a martingale if
![\begin{equation*}
X_t = \mathbb{E}[X_{t + i} \mid \mathcal{F}_t], \quad i \ge 0
\end{equation*}](../../assets/latex/probability_and_statistics_270a8ecf4eafe631538496cac4746d3846577297.png)
where

Examples
- Simple random walk is a martingale
- Balance of a Roulette player is NOT martingale
Optional stopping theorem
A given stochastic process  , a non-negative integer r.v.
, a non-negative integer r.v.  is called a stopping time if
is called a stopping time if

depends only on  (i.e. stopping at some time
(i.e. stopping at some time  only depends on the first
only depends on the first  r.v.s).
r.v.s).
This implies that if we a process can be described as a martingale, then it's a "zero-sum".
Continuous
Lévy process
A stochastic process  is said to be a Lévy process if it satisfies the following properties:
is said to be a Lévy process if it satisfies the following properties:
 almost surely.
almost surely.- Independence of increments: for any $0 ≤ t1 ≤ t2 ≤ … ≤ tn < ∞, the increments
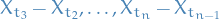 are independent.
are independent. - Stationary increments: For any
 , the rvs.
, the rvs.  is equal in distribution to
is equal in distribution to  .
. Continuity in probability: For any
 and
and  it holds that
it holds that

If  is a Lévy process then one may construct a version of
is a Lévy process then one may construct a version of  such that
such that  is almost surely right-continuous with left limits.
is almost surely right-continuous with left limits.
Wiener process
The Wiener process (or Brownian motion) is a continuous-time stochastic process  characterized by the following properties:
characterized by the following properties:
 (almost surely)
(almost surely)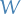 has independent increments: for
has independent increments: for  , future increments
, future increments  with
with  , are independent of the past values
, are independent of the past values 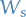 ,
, 
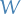 has Gaussian increments:
has Gaussian increments:
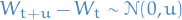
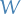 has continuous paths: with probability
has continuous paths: with probability  ,
,  is continuous in
is continuous in 
Further, let 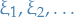 be i.i.d. rv. with mean 0 and variance 1. For each
be i.i.d. rv. with mean 0 and variance 1. For each  , define the continuous-time stochastic process
, define the continuous-time stochastic process
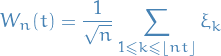
Then

i.e. a random walk approaches a Wiener process.
Properties
Let  be the first time such that
be the first time such that

Then

Observe that
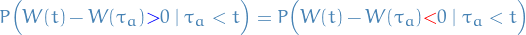
which is saying that at the point  we have
we have  , and therefore for all time which follows we're equally likely to be above or below
, and therefore for all time which follows we're equally likely to be above or below  .
.
Therefore
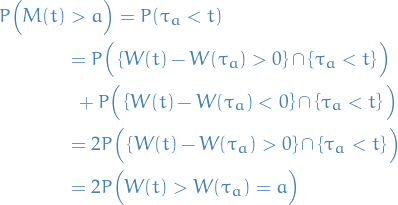
where in the last inequality we used the fact that the set of events  .
.
This theorem helps us solve the gambler's ruin problem!
Let  denote your bankroll at time
denote your bankroll at time  , and at each
, and at each  it changes by
it changes by
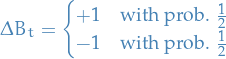
The continuous approximation of this process is given by a Brownian motion, hence we can write the bankroll as

where  denotes a Brownian motion (with
denotes a Brownian motion (with ![$\mathbb{E}[W_t] = 0$](../../assets/latex/probability_and_statistics_7a7e0761a608ecf7946800a88f5b331d904e6ff3.png) ).
).
We're interested in how probable it is for us to be ruined before some time  . Letting
. Letting  be the time were we go bankrupt, we have
be the time were we go bankrupt, we have
i.e. that we hit the time were we go bankrupt before time  .
.
Bankrupt corresponds to

where  denotes a Wiener process (hence centered at 0).
denotes a Wiener process (hence centered at 0).
Then we can write

where the last equality is due to the symmetry of a Normal distribution and thus a Brownian motion.
Hence

where  denotes a standard normal distribution.
denotes a standard normal distribution.
![\begin{equation*}
\lim_{n \to \infty} \Big[ B \Big(T (t / n) \Big) - B\Big(T (t - 1) / n \Big) \Big]^2 = T
\end{equation*}](../../assets/latex/probability_and_statistics_d2676857ceb9dd02ba9d8dd6aa20b7abc46bcd3c.png)
This is farily straightforward to prove, just recall the Law of Large numbers and you should be good.
Non-differentiability
 is non-differentiable with probability 1.
is non-differentiable with probability 1.
Suppose, for the sake of contradiction, that  is differentiable with probability 1.
Then, by MVP we have
is differentiable with probability 1.
Then, by MVP we have

for some 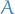 and all
and all  . This implies that
. This implies that
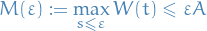
since  .
.
Hence
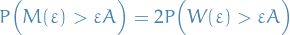
As  , since
, since 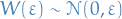 , then
, then

where

Thus, when  , we have
, we have

since  Hence,
Hence,

contracting our initial statement.
Geometric Brownian motion
A stochast process  is said to follow a Geometric Brownian Motion if it satisfies the following stochastic differential equation (SDE):
is said to follow a Geometric Brownian Motion if it satisfies the following stochastic differential equation (SDE):

where  is the Brownian motion, and
is the Brownian motion, and  (percentage drift) and
(percentage drift) and  (percentage volatility) are constants.
(percentage volatility) are constants.
Brownian bridge
A Brownian bridge is a continuous-time stochastic process  whose probability distribution is the conditional probability distribution of a Brownian motion
whose probability distribution is the conditional probability distribution of a Brownian motion  subject to the condition that
subject to the condition that

so that the process is pinned at the origin at both  and
and 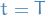 . More precisely,
. More precisely,
![\begin{equation*}
B_t := \big( W_t \mid W_T = 0 \big), \quad t \in [0, T]
\end{equation*}](../../assets/latex/probability_and_statistics_8238711534767675a010b92c07f261a709260728.png)
Then
![\begin{equation*}
\mathbb{E}[B_t] = 0, \quad \text{Var}(B_t) = \frac{t (T - t)}{T}
\end{equation*}](../../assets/latex/probability_and_statistics_400aba49f998227142fefa7ee51e38a6da33a6af.png)
implying that the most uncertainty is in the middle of the bridge, with zero uncertainty at the nodes.
Sometimes the notation  is used for a Wiener process / Brownian motion rather than for a Brownian bridge.
is used for a Wiener process / Brownian motion rather than for a Brownian bridge.
Markov Chains
Notation
 denotes the transition matrix (assumed to be ergodic, unless stated otherwise)
denotes the transition matrix (assumed to be ergodic, unless stated otherwise)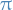 is the stationary distribution
is the stationary distribution denotes the initial state
denotes the initial state is the state space
is the state space denotes an uncountable state space
denotes an uncountable state space denotes
denotes  which means all points except those with zero-measure, i.e.
which means all points except those with zero-measure, i.e.  such that
such that 
Definitions
A Markov chain is said to be irreducible if it's possible to reach any state from any state.
A state  has a period
has a period  if any return to state
if any return to state  must occur in multiples of
must occur in multiples of  time steps.
time steps.
Formally, the period of a state is defined as
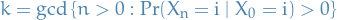
provided that the set is non-empty.
A state  is said to be transient if, given that we start in state
is said to be transient if, given that we start in state  ,t there is a non-zero probability that we will never return to
,t there is a non-zero probability that we will never return to  .
.
A state  is said to be recurrent (or persistent) if it is not transient, i.e. gauranteed (with prob. 1) to have a finite hitting time.
is said to be recurrent (or persistent) if it is not transient, i.e. gauranteed (with prob. 1) to have a finite hitting time.
A state  is said to be ergodic if it is aperiodic and positive recurrent, i.e.
is said to be ergodic if it is aperiodic and positive recurrent, i.e.
- aperiodic: period of 1, i.e. can return to current state in a single step
- positive recurrent: has a finite mean recurrence time
If all states in an irreducible Markov chain are ergodic , then the chain is said to be ergodic.
The above definitions can be generalized to continuous state-spaces by considering measurable sets  rather than states
rather than states  . E.g. recurrence now means that for any measurable set
. E.g. recurrence now means that for any measurable set  , we have
, we have

where  denotes the number of steps we need to take until we "hit"
denotes the number of steps we need to take until we "hit" 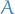 , i.e. the hitting time.
, i.e. the hitting time.
[This is a personal thought though, so not 100% guaranteed to be correct.]
Coupling
- Useful for bouding the mixing rate of Markov chains, i.e. the number of steps it takes for the Markov chain to converge to the stationary distribution
Distance to Stationary Distribution
Use Total Variance as a distance measure, therefore convergence is defined through

 denotes the variation distance between two Markov chain random variables
denotes the variation distance between two Markov chain random variables  and
and  , i.e.
, i.e.

One can prove that

which allows us to bound the distance between a chain and the stationary distribution, by considering the difference between two chains, without knowing the stationary distribution!
Coupling
Let  and
and  be random variables with probability distributions
be random variables with probability distributions  and
and  on
on  , respectively.
, respectively.
A distribution  on
on  is a coupling if
is a coupling if
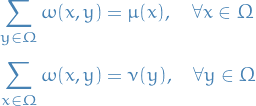
Consider a pair of distributions  and
and  on
on  .
.
For any coupling
 of
of  and
and  , with
, with 

There always exists a coupling
 s.t.
s.t.

Observe that

Therefore,
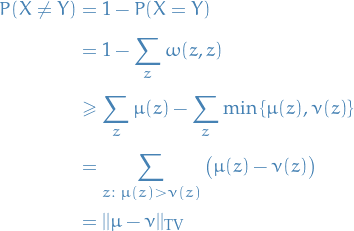
Concluding the proof.
"Inspired" by our proof in 1., we fix diagonal entries:

to make one of the inequalities an equality. Now we simply need to construct
 such that the above is satisfied, and it's a coupling. One can check that
such that the above is satisfied, and it's a coupling. One can check that
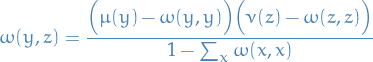
does indeed to the job.
Ergodicity Theorem
If  is irreducible and aperiodic, then there is a unique stationary distribution
is irreducible and aperiodic, then there is a unique stationary distribution  such that
such that
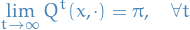
Consider two copies of the Markov chain  and
and 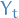 , both following
, both following  . We create the coupling distribution as follows:
. We create the coupling distribution as follows:
- If
 , then choose
, then choose  and
and  independently according to
independently according to 
- If
 , choose
, choose 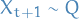 and set
and set 
From the couppling lemma, we know that

Due to ergodicity, there exists  such that
such that 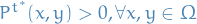 . Therefore, there is some
. Therefore, there is some  such that for all initial states
such that for all initial states 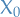 and
and 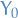 ,
,

Similarily, due to the Markovian property, we know

Since
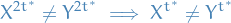
we have
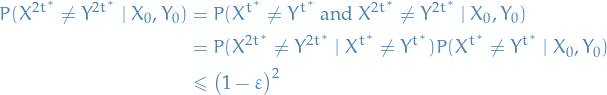
Hence, for any positive integer  :
:

Hence,
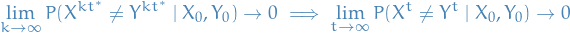
Coupling lemma then gives

Finally, we observe that, letting  ,
,
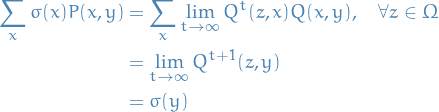
which shows that  , i.e. converges to the stationary distribution.
, i.e. converges to the stationary distribution.
Finally, observe that  is unique, since
is unique, since

Mixing time
Let  be some
be some  and let
and let 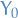 have the stationary distribution. Fix
have the stationary distribution. Fix  .
By the coupling lemma, there is a coupling and random variables
.
By the coupling lemma, there is a coupling and random variables  and
and  such that
such that

Using this coupling, we define a coupling of the distributions of 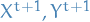 as follows:
as follows:
- If
 , set
, set 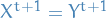
- Else, let
 and
and  independently
independently
Then we have,

The first inequality holds due to the coupling lemma, and the second inequality holds by construction of the coupling.
Since  never decreases, we can define the mixing time
never decreases, we can define the mixing time  of a Markov chain as
of a Markov chain as

for some chosen  .
.
General (uncountable) state space
Now suppose we have some uncountable state-space  . Here we have to be a bit more careful when going about constructing Markov chains.
. Here we have to be a bit more careful when going about constructing Markov chains.
- Instead of considering transitions
 for some
for some  , we have to consider transitions
, we have to consider transitions  for
for  and
and  .
.
- Transition probability is therefore denote

- Transition probability is therefore denote
- This is due to the fact that typically, the measure of a singleton set
 is zero, i.e.
is zero, i.e.  , when we have an uncountable number possible inputs.
, when we have an uncountable number possible inputs. - That is; we have to consider transitions to subsets of the state-space, rather than singletons
- This requires a new definition of irreducibility of a Markov chain
A chain is  if there exists a non-zero sigma-finite measure
if there exists a non-zero sigma-finite measure  on
on  such that for all
such that for all  with
with  (i.e. all non-zero measurable subsets), and for all
(i.e. all non-zero measurable subsets), and for all  , there exists a positive integer
, there exists a positive integer  such that
such that
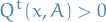
We also need a slightly altered definition of periodicity of a Markov chain:
A Markov chain with stationary distribution 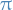 is periodic if there exist
is periodic if there exist  and disjoint subsets
and disjoint subsets  with
with

and
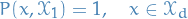
such that 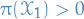 , and hence
, and hence  for all
for all  . That is, we always transition between subsets, and never within these disjoint subsets.
. That is, we always transition between subsets, and never within these disjoint subsets.
If such does not exist, i.e. the chain is not periodic, then we say the chain is aperiodic.
Results such as the coupling lemma also hold for the case of uncountable state-space, simply by replacing the summation with the corresponding integrand over the  . From roberts04_gener_state_space_markov_chain_mcmc_algor, similarily to the countable case, we have the following properties:
. From roberts04_gener_state_space_markov_chain_mcmc_algor, similarily to the countable case, we have the following properties:
Let  and
and  be probability measures on the space
be probability measures on the space  . Then
. Then
![$||\mu - \nu||_{\rm{TV}} = \sup_{f : \mathcal{X} \to [0, 1]} \left| \int f d \mu - \int f d \nu \right|$](../../assets/latex/probability_and_statistics_381334c21ab2d08946d2920a57405b378136dc70.png)
More generally,
![\begin{equation*}
||\mu - \nu||_{\rm{TV}} = \frac{1}{b - a} \sup_{f: \mathcal{X} \to [a, b]} \left| \int f \ d \mu - \int f \ d \nu \right|
\end{equation*}](../../assets/latex/probability_and_statistics_7f1df4fa4639c3eac471ad5d77867381654a9621.png)
In particular,
![\begin{equation*}
||\mu - \nu||_{\rm{TV}} = \frac{1}{2} \sup_{f: \mathcal{X} \to [-1, 1]} \left| \int f \ d \mu - \int f \ d \nu \right|
\end{equation*}](../../assets/latex/probability_and_statistics_5fc1b80015a31e2ab01be527365a3eb8647b7be4.png)
If
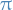 is a stationary distribution for a Markov chain with kernel
is a stationary distribution for a Markov chain with kernel  , then
, then  is non-increasing in
is non-increasing in  , i.e.
, i.e.

for
 .
.
More generally, letting
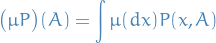
we always have
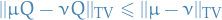
If
 and
and  have densities
have densities 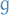 and
and  , respectively, wrt. to some sigma-finite measure
, respectively, wrt. to some sigma-finite measure  , then
, then
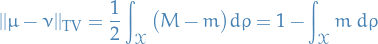
with

Given probability measures
 and
and  , there are jointly defined random variables
, there are jointly defined random variables  and
and  such that
such that

and
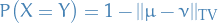
From roberts04_gener_state_space_markov_chain_mcmc_algor we also have the following, important theorem:
If a Markov chain on a state space with countable generated sigma-algebra is  irreducible and aperiodic, and has a stationary distribution
irreducible and aperiodic, and has a stationary distribution 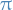 , then for
, then for 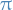 almost-every
almost-every  ,
,

In particular,

We also introduce the notion of Harris recurrent:
We say a Markov chain is Harris recurrent if for all  with
with 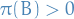 (i.e. all non-zero-measurable subsets), and all
(i.e. all non-zero-measurable subsets), and all  , the chain will eventually reach
, the chain will eventually reach  from
from  with probability 1, i.e.
with probability 1, i.e.
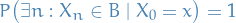
This notion is stronger than the notion of irreducibility introduced earlier.
Convergence rates
Uniform Ergodicity
From this theorem, we have implied asymptotic convergence to stationarity, but it does not provide us with any information about the rate of convergence. One "qualitative" convergence rate property is
A Markov chain having stationary distribution 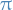 is uniformly ergodic if
is uniformly ergodic if

for some  and
and  .
.
For further developments of ensuring uniform ergodicity, we need to define
A subset  is small or
is small or  if there exists a positive integer
if there exists a positive integer  ,
,  , and a probability measure
, and a probability measure  on
on  s.t. the following minorisation condition holds:
s.t. the following minorisation condition holds:
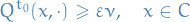
i.e. 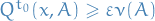 for all
for all  and all measurable
and all measurable  .
.
Geometric ergodicity
A Markov chain with stationary distribution 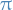 is geometrically ergodic if
is geometrically ergodic if
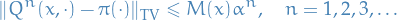
for some  where
where 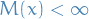 for
for 
 .
.
Difference between uniform ergodicity and geometric ergodicity is the fact that in geometric ergodicity the 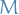 can also depend on the initial state
can also depend on the initial state  .
.
In practice
Diagnostics
Effective sample size (ESS)
(split)  statistic
statistic
- Consider running
 chains, each for
chains, each for  steps, from different initializations
steps, from different initializations  , where
, where  is even
is even - Then consider splitting each chain in half, resulting in two half-chains for each chain, leaving us with a total of
 chains
chains
- Reason: If a chain indeed represents independent samples from the stationary distribution, then at the very least the first half and second half of the chain should indeed have the display similar behavior (for sufficiently large
 )
)
- Reason: If a chain indeed represents independent samples from the stationary distribution, then at the very least the first half and second half of the chain should indeed have the display similar behavior (for sufficiently large
You might wonder, why not split in 3? Or 4? or, heck,  ?!
?!
Likely answer: "You could, but be sensible!" Very unsatisfying…
Let 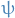 be the scalar estimand, i.e. the variable we're trying to estimate. Let
be the scalar estimand, i.e. the variable we're trying to estimate. Let  be the "for
be the "for  and
and  denote the different samples for the variable of interest
denote the different samples for the variable of interest 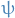 obtained by
obtained by  MCMC chains, each with
MCMC chains, each with  samples each, with different initializations.
samples each, with different initializations.
We denote the (B)etween- and (W)ithin-sequence variances
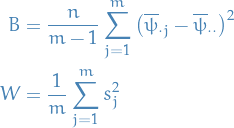
where
empirical mean within a chain
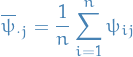
empirical mean across all chains
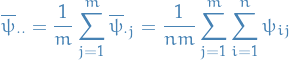
empirical variance within each chain
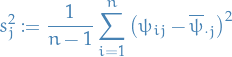
Notice that  contains a factor of
contains a factor of  because it is based on the variance of the within-sequence means
because it is based on the variance of the within-sequence means  , each of which is an averaeg of
, each of which is an averaeg of  values
values  .
.
We can then estimate  , the marginal posterior variance of the estimand, by a weighted average of
, the marginal posterior variance of the estimand, by a weighted average of 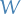 and
and  , namely
, namely
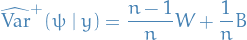
Finally, we can then monitor convergence of the iterative simulation by estimating the factor by which the scale of the current distribution for 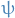 might be reduced if the simulations were continued in the limit
might be reduced if the simulations were continued in the limit  . This potential scale reduction is estimated by
. This potential scale reduction is estimated by

which has the property that
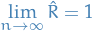
(remember that  depend on
depend on  ).
).
If
 is large → reason to believe that further simulations may improve our inference about the target distribution of the associated scalar estimand
is large → reason to believe that further simulations may improve our inference about the target distribution of the associated scalar estimand is small → ???
is small → ???
Specific distributions & processes
Hazard function
The hazard function / failure rate  is defined
is defined
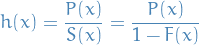
where  denotes the PDF and
denotes the PDF and  denotes the CDF.
denotes the CDF.
TODO Renewal processes
- Let
 with
with  be a sequence of waiting times between
be a sequence of waiting times between 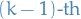 and the
and the 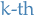 event.
event. Arrival time of the
 event is
event is
- Denote
 by the total number of events in
by the total number of events in 
- If
 is fixed, then
is fixed, then  is the count variable we wish to model
is the count variable we wish to model
It follows that

i.e. total number of events is less than
 if and only if the arrival time of the
if and only if the arrival time of the  event is greater than
event is greater than  , which makes sense
, which makes sense
If
 is the distribution function of
is the distribution function of  , we have
, we have

Furthermore
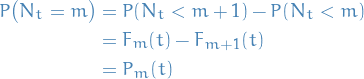
- This is the fundamental relationship between the count variable
 and the timing process
and the timing process 
- This is the fundamental relationship between the count variable
- If
 , the process is called a renewal process
, the process is called a renewal process In this case, we can extend the above equation to the following recursive relationship:
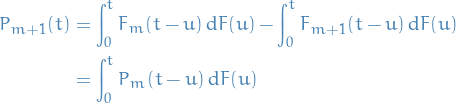
where we have

- Intuitively: probability of exactly
 events occuring by time
events occuring by time  is the probability that the first event occurs at time
is the probability that the first event occurs at time  , and that exactly
, and that exactly  events occur in the remaining time interval, integrated over all times
events occur in the remaining time interval, integrated over all times  .
. - Evaluting this integral, we can obtain
 from the above recursive relationship.
from the above recursive relationship.
- Intuitively: probability of exactly
Weibull renewal process
Statistics
Notation
 denotes
denotes  converges in probability to
converges in probability to 
 denotes
denotes  convergence in law to
convergence in law to 
Definitions
Efficency
The efficency of an unbiased estimator  is the ratio of the minimum possible variance to
is the ratio of the minimum possible variance to  .
.
An unbiased estimator with efficiency equal to 1 is called efficient or a minimum variance unbiased estimator (MVUE).
Statistic
Suppose a random vector  has distribution function in a parametric family
has distribution function in a parametric family  and realized value
and realized value  .
.
A statistic is r.v.  which is a function of
which is a function of  independent of
independent of  . Its realized value is
. Its realized value is  .
.
A statistic  is said to be sufficient for
is said to be sufficient for  if the distribution of
if the distribution of  given
given  does not depend on
does not depend on  , i.e.
, i.e.

Further, we say  is a minimal sufficient statistic if it's the smallest / least complex "proxy" for
is a minimal sufficient statistic if it's the smallest / least complex "proxy" for  .
.
Observe that,
- if
 is sufficient for
is sufficient for  , so is any one-to-one function of
, so is any one-to-one function of 
 is trivially sufficient
is trivially sufficient
We say a statistic is pivotal if it does not depend on any unknown parameters.
E.g. if we are considering a normal distribution  and
and  is known, then the mean could be a pivotal statistic, since we know all information about the distribution except the statistic itself. But if we didn't know
is known, then the mean could be a pivotal statistic, since we know all information about the distribution except the statistic itself. But if we didn't know  , the mean would not be pivotal.
, the mean would not be pivotal.
Let  .
.
Then statistic 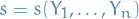 is sufficient for
is sufficient for  if and only if there exists functions
if and only if there exists functions  of
of  and
and  of
of  such that
such that

where  denotes the likelihood.
denotes the likelihood.
U-statistic
Let  be independent observations on a distribution
be independent observations on a distribution  .
.
Consider a "parametric function"  for which there is an unbiased estimator. That is,
for which there is an unbiased estimator. That is,  may be represented as
may be represented as
![\begin{equation*}
\theta(F) = \mathbb{E}_F \big[ h(X_1, \dots, X_m) \big] = \int \dots \int h(x_1, \dots, x_m) \dd{F(x_1)} \cdots \dd{F(x_m)}
\end{equation*}](../../assets/latex/probability_and_statistics_d65325ac98ad0431810d295a5d19bfb7fe5b58ee.png)
for some function  , called a kernel.
, called a kernel.
Without loss of generality, we may assume  is symmetric, otherwise we could simply
is symmetric, otherwise we could simply

For any kernel  , the corresponding U-statistic for estimation of
, the corresponding U-statistic for estimation of  on the basis of a sample
on the basis of a sample  for size
for size  is obtained by averaging the kernel
is obtained by averaging the kernel  symmetrically over the observations:
symmetrically over the observations:
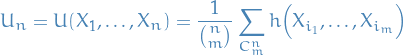
where  denotes the summation over
denotes the summation over  combinations of
combinations of  distinct elements
distinct elements  from
from  .
.
Clearly,  is then an unbiased estimate of
is then an unbiased estimate of  .
.
To conclude, a U-statistic is then a statistic which has the property of being an unbiased estimator for the corresponding  , where
, where  is such that it can be written stated above.
is such that it can be written stated above.
V-statistic
Statistics that can be represented as functionals  of the empirical distribution function,
of the empirical distribution function,  , are called statistical functionals.
, are called statistical functionals.
A V-statistic is a statistical function (of a sample) defined by a particular statistical functional of a probability distribution.
Suppose  is a sample. In typical applications the statistical function has a representation as the V-statistic
is a sample. In typical applications the statistical function has a representation as the V-statistic

where  is a symmetric kernel function.
is a symmetric kernel function.
 is called a V-statistic of degree
is called a V-statistic of degree  .
.
Seems very much like a form of boostrap-estimate, does it not?
Informally, the type of asymptotic distribution of a statistical function depends on the order of "degeneracy," which is determined by which term is the first non-vanishing term in the Taylor expansion of the functional  .
.
Quantiles
Let  be a random variable with cumulative density function (CDF)
be a random variable with cumulative density function (CDF)  , i.e.
, i.e.
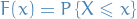
Let 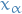 be such that
be such that

for some ![$\alpha \in [0, 1]$](../../assets/latex/probability_and_statistics_df706ca088cfab3f5c3067f3ca880bfddf0f6fa5.png) .
.
Then we say that 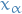 is called the
is called the  quantile of
quantile of  , i.e. the value such that
, i.e. the value such that
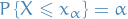
We then say:
 is the median; half probability mass on each side
is the median; half probability mass on each side is the lower quantile
is the lower quantile is the upper quantile
is the upper quantile
 is strictly monotonically increasing so
is strictly monotonically increasing so  exists, hence we can compute the quantiles!
exists, hence we can compute the quantiles!
Convergence in law
A sequence of cdfs  is said to converge to
is said to converge to  iff
iff  on all continuity points of
on all continuity points of  .
.
We say that if a random variable  has cdf
has cdf  and the rv
and the rv  has cdf
has cdf  , then
, then  converges in law to
converges in law to  , and we write
, and we write
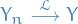
This does not mean that  and
and  are arbitrarily close as random variables. Consider the random variables
are arbitrarily close as random variables. Consider the random variables  and
and  .
.
Let  and
and  be random variables. Then
be random variables. Then
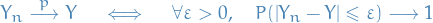
where  means converges in probability.
means converges in probability.
Or, equivalently

This is the notion used by WLLN.
If  where
where  is the limit distribution and
is the limit distribution and  then
then

Let  be a sequence of random variables, and
be a sequence of random variables, and  be a random variable.
be a random variable.
Then

This is the notion of convergence used by SLLN.
Kurtosis
The kurtosis of a random variable is the 4th moment, i.e.
![\begin{equation*}
\text{Kurt}[X] = \kappa(X) = \mathbb{E} \Bigg[ \bigg( \frac{X - \mu}{\sigma} \bigg)^4 \Bigg] = \frac{\mu_4}{\sigma^4} = \frac{\mathbb{E}[(X - \mu)^4]}{\big(\mathbb{E}[(X - \mu)^2]\big)^2}
\end{equation*}](../../assets/latex/probability_and_statistics_999127ed41a92556298ca94fe627e7880cb44028.png)
where  denotes the 4th central moment and
denotes the 4th central moment and  is the std. dev.
is the std. dev.
Words
A collection of random variables is homoskedastic if all of these random variables have the same finite variance.
This is also known as homogeneity of variance.
A collection of random variables is heteroskedastic if there are sub-populations that have different variability from others.
Thus heteroskedasticity is the absence of homoskedastic.
Consistency
Loosely speaking, an estimator  of parameter
of parameter  is said to be consistent, if it converges in probability to the true value of the parameter:
is said to be consistent, if it converges in probability to the true value of the parameter:
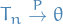
Or more rigorously, suppose  is a family of distributions (the parametric model) and
is a family of distributions (the parametric model) and 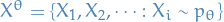 is an infinite sample from the distribution
is an infinite sample from the distribution  .
.
Let  be a sequence of estimators for some parameter
be a sequence of estimators for some parameter  . Usually
. Usually  will be based on the first
will be based on the first  observations of a sample. Then this sequence is said to be (weakly) consistent if
observations of a sample. Then this sequence is said to be (weakly) consistent if

Jeffreys Prior
The Jeffreys prior is a non-informative prior distribution for a parameter space, defiend as:

It has the key feature that it is invariant under reparametrization.
Moment generating function
For r.v.  the moment generating function is defined as
the moment generating function is defined as
![\begin{equation*}
M_x(t) = \mathbb{E} [e^{tX}], \quad t \in \mathbb{R}
\end{equation*}](../../assets/latex/probability_and_statistics_478db7622be48bf5634482c422f45780b09638e0.png)
Taking the derivative wrt.  we observe that
we observe that
![\begin{equation*}
\frac{\partial M_x}{\partial t} = \mathbb{E}[X e^{tX}]
\end{equation*}](../../assets/latex/probability_and_statistics_b737676d842bc4dfef42eab4fb0aaf297a3623ba.png)
Letting  , we get
, we get
![\begin{equation*}
\frac{\partial M_x}{\partial t} = \mathbb{E}[X]
\end{equation*}](../../assets/latex/probability_and_statistics_e540fafcfcf7bb424d3e256240d9ee11a3f94635.png)
i.e. the mean. We can take this derivative  times to obtain the expectation of
times to obtain the expectation of  , which is why
, which is why  is useful.
is useful.
Distributions
Binomial
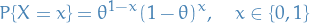
or equivalently,
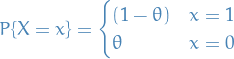
Negative binomial
A negative binomial random variable represents the number of success  before obtaining
before obtaining  failures, where
failures, where  is the probability of a failure for each of these binomial rvs.
is the probability of a failure for each of these binomial rvs.
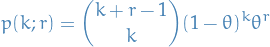
Derivation
Let  denote the rv. for # of successes and
denote the rv. for # of successes and  the number of failures.
the number of failures.
Suppose we have a run of 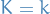 successes and
successes and 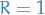 failure, then
failure, then
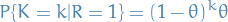
where the failure is of course the last thing that happens before we terminate the run.
Now, suppose that the run above is followed up by  failures, i.e.
failures, i.e. 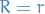 but we have a specific ordering. Then, letting
but we have a specific ordering. Then, letting  denote the result of the i-th Binomial trail,
denote the result of the i-th Binomial trail,
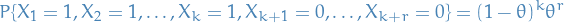
But for  of the failures, we don't actually care when they happen, so we don't want any ordering. That is, we have
of the failures, we don't actually care when they happen, so we don't want any ordering. That is, we have 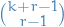 sequences of the form described above which are acceptable.
sequences of the form described above which are acceptable.
Hence we get the pmf
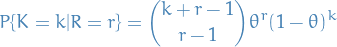
Gamma distribution
Chi-squared distribution
The chi-squared distribution with  degrees of freedom is the distribution of a sum of the squares of
degrees of freedom is the distribution of a sum of the squares of  independent standard normal random variables.
independent standard normal random variables.
It's a special case of the gamma distribution.
T-distribution
The T-distribution arises as a result of the Bessel-corrected sample variance.
Why?
Our population-model is as follows:

Let
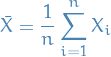
then let
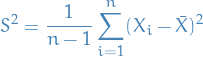
be the Bessel-corrected variance. Then the random variable
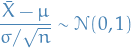
and the random variable
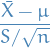
(where  has been substituted for
has been substituted for  ) has a Student's t-distribution with
) has a Student's t-distribution with 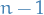 degrees of freedom.
degrees of freedom.
Note that the numerator and the denominator in the preceding expression are independent random variables, which can be proved by a simple induction.
F-distribution
A random variate of the F-distribution with parameters  and
and 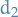 arises as the ratio of the two appropriately scaled chi-quared variates:
arises as the ratio of the two appropriately scaled chi-quared variates:
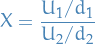
where
 and
and 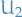 have a chi-squared distribution with
have a chi-squared distribution with  and
and 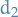 degrees of freedom respectively
degrees of freedom respectively and
and 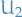 are independent
are independent
Power laws
Notation
 such that we have a power law
such that we have a power law 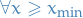 , in such cases we say that the tail of the distribution follows a power law
, in such cases we say that the tail of the distribution follows a power law
Definition
A continuous power-law is one described by probability density 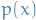 such that
such that

where  is the observed value and
is the observed value and  is the normalization constant. Clearly this diverges as
is the normalization constant. Clearly this diverges as  , hence cannot hold for all
, hence cannot hold for all  ; must be a lower bound to power-law behavior.
; must be a lower bound to power-law behavior.
Provided  , we have
, we have
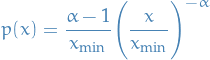
A discrete power-law is defined by
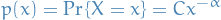
Again, diverges at zero, hence must be some lb  on power-law behaviour:
on power-law behaviour:
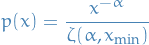
where
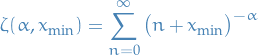
is the generalized or Hurwitz zeta function.
Important
Sources: clauset07_power_law_distr_empir_data and so_you_think_you_have_a_power_law_shalizi
- Log-log plot being roughly linear is necessary but not sufficient
- Errors are hard to estimate because they are not well-defined by the usual regression formulas, which are based on assumptions that do not apply in this case: noise of logarithm is not Gaussian as assumed by linear regression. In continuous case, this can be made worse by choice of binning scheme used to construct histogram, hence we have an additional free parameter.
- A fit to a power-law distribution can account for a large fraction of the variance even when fitted data do not follow a power law, hence high values of
 ("explained variance by regression fit") cannot be taken as evidence in favor of the power-law form.
("explained variance by regression fit") cannot be taken as evidence in favor of the power-law form. - Fits extracted by regression methods usually do not satisfy basic requirements on probability distributions, such as normalization and hence cannot be correct.
- Abusing linear regression. Standard methods, e.g. least-squares fitting are known to produce systematically biased estimates of parameters for power-law distributions and should not be used in most circumstances
- Use MLE to estimate scaling exponent

- Use goodness of fit to estimate scaling regions.
- In some cases there are only parts of the data which actually follows a power law.
- Method based on Kolmogorv-Smirnov goodness-of-fit statistic
- Use goodnes-of-fit test to check goodness of fit
- E.g. Kolmogorov-Smirnov test to check data drawn from estimated power law vs. real data
- Use Vuong's test to check for alternative non-power laws (see likelihood_ratio_test_for_model_selection_and_non_nested_hypothesis_vyong89)
Maximum Likelihood Estimation
Notation
 denotes the log-likelihood , i.e.
denotes the log-likelihood , i.e. 
 is the Fisher's information (expected information)
is the Fisher's information (expected information)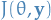 is the observed information , i.e. information without taking the expectation
is the observed information , i.e. information without taking the expectation is called the score function
is called the score function denotes that true (and thus unobserved) parameter
denotes that true (and thus unobserved) parameter means the probability density
means the probability density 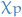 evaluated at
evaluated at 
Appoximate (asymptotic) variance of MLE
For large samples (and under certain conditions ) the (asymptotic) variance of the MLE  is given by
is given by

where
![\begin{equation*}
I_\theta = \mathbb{E} \Bigg( \Bigg[ \frac{dl}{d\theta} \Bigg]^2 \Bigg) = - \mathbb{E} \Bigg( \frac{d^2 l}{d\theta^2} \Bigg)
\end{equation*}](../../assets/latex/probability_and_statistics_c6026d15fa470bb7097a7a0dde8138840c1a4282.png)
where  is called the Fisher information .
is called the Fisher information .
Estimated standard error
The estimated standard error of the MLE  of
of  is given by
is given by
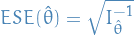
Regularity conditions
The lower bound of the variance of the MLE is true under the following conditions on the probability density function,  , and the estimator
, and the estimator  :
:
- The Fisher information is always defined; equivalently for all
 such that
such that  :
:

exists and is finite.
- The operations of integration wrt. to
 and differentiation wrt.
and differentiation wrt.  can be interchanged in the expectation of
can be interchanged in the expectation of  ; that is,
; that is,
![\begin{equation*}
\frac{\partial}{\partial \theta} \Bigg[ \int T(x) f(x;\theta) \ dx \Bigg] = \int T(x) \Big[ \frac{\partial}{\partial \theta} f(x; \theta) \Big] \ dx
\end{equation*}](../../assets/latex/probability_and_statistics_6c64d356fe0aa2961efd3466b02125c5a6e1c96a.png)
whenever the RHS is finite. This condition can often be confirmed by using the fact that integration and differentiation can be swapped when either of the following is true:
- The function
 has bounded support in
has bounded support in  , and the bounds do not depend on
, and the bounds do not depend on 
- The function
 has infinite support, is continuously differentiable, and the integral converges uniformly for all
has infinite support, is continuously differentiable, and the integral converges uniformly for all 
Proof (single variable)
"Proof" (alternative, also single variable)
- Notation
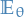 denotes the expectation over the data
denotes the expectation over the data  , assuming the data arises from the model specified by the parameter
, assuming the data arises from the model specified by the parameter 
 is the same as above, but assuming
is the same as above, but assuming 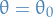
 denotes the score, where we've made the dependence on the data
denotes the score, where we've made the dependence on the data  explicit by including it as an argument
explicit by including it as an argument
- Stuff
- Consistency of
 as an estimator
as an estimator
Suppose the true parameter is
 , that is:
, that is:

Then, for any
 (not necessarily
(not necessarily  ), the Law of Large Numbersimplies the convergence in probability
), the Law of Large Numbersimplies the convergence in probability
![\begin{equation*}
\frac{1}{n} \sum_{i=1}^{n} \log f(X_i \mid \theta) \to \mathbb{E}_{\theta_0}[\log f(X \mid \theta)]
\end{equation*}](../../assets/latex/probability_and_statistics_38a1afa016cb0802911d69d3fb99b6c48d855b5c.png)
Under suitable regularity conditions, this implies that the value of
 maximizing the LHS, which is
maximizing the LHS, which is  , converges in probability to the value of
, converges in probability to the value of  maximizing RHS, which we claim is
maximizing RHS, which we claim is  .
.
Indeed, for any

![\begin{equation*}
\mathbb{E}_{\theta_0}[ \log f(X \mid \theta)] - \mathbb{E}_{\theta_0} [ \log f(X \mid \theta_0)] = \mathbb{E}_{\theta_0} \Bigg[ \log \frac{f(X \mid \theta)}{f(X \mid \theta_0} \Bigg]
\end{equation*}](../../assets/latex/probability_and_statistics_8a065868d54f7d3f27f9eaa55dee2843d2a54aa5.png)
Noting that
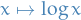 is concave, Jensen's Inequality implies
is concave, Jensen's Inequality implies
![\begin{equation*}
\mathbb{E}[\log X] \le \log \mathbb{E}[X]
\end{equation*}](../../assets/latex/probability_and_statistics_c3d09c146a6ce43fab76633e4dfca4ca0d6f58cd.png)
for any positive random variable
 , so
, so
![\begin{equation*}
\begin{split}
\mathbb{E}_{\theta_0}\Bigg[ \log \frac{f(X \mid \theta)}{f(X \mid \theta_0)} \Bigg] & \le \log \mathbb{E}_{\theta_0} \Bigg[ \frac{f(X \mid \theta)}{f(X \mid \theta_0)} \Bigg] \\
& = \log \int \frac{f(x \mid \theta)}{f(x \mid \theta_0)} f(x \mid \theta_0) \ dx \\
&= \log \int f(x \mid \theta_0) \ dx \\
&= 0
\end{split}
\end{equation*}](../../assets/latex/probability_and_statistics_0ed41b771f87ebc4eb100285a0baf81662be5549.png)
Which establishes "consistency" of
 since
since ![$\theta \mapsto \mathbb{E}_{\theta_0}[\log f(X \mid \theta)]$](../../assets/latex/probability_and_statistics_95959728964caee763d8ae36db8189c9c744e019.png) is maximized at
is maximized at  .
.
- Expectation and variance of score
For
 ,
,
![\begin{equation*}
\mathbb{E}_{\theta}[U(X, \theta)] = 0, \qquad \text{Var}_{\theta} \big( U(X, \theta) \big) = - \mathbb{E}[U'(X, \theta)]
\end{equation*}](../../assets/latex/probability_and_statistics_64bc641e48dae229ceb7b967982458f04c4273ae.png)
First, for the expectation we have
![\begin{equation*}
\begin{split}
\mathbb{E}_{\theta}[U] &= \int U(x, \theta) f(x; \theta) \ dx \\
&= \int \Bigg( \frac{\partial \log f(x; \theta)}{\partial \theta} \Bigg) f(x; \theta) \ dx \\
&= \int \Bigg( \frac{1}{f(x; \theta)} \frac{\partial f}{\partial \theta} \Bigg) f(x; \theta) \ dx \\
&= \int \frac{\partial f}{ \partial \theta} \ dx
\end{split}
\end{equation*}](../../assets/latex/probability_and_statistics_2992b8afaa3afeabbdde632f36d8abfb74e8a772.png)
Assuming we can interchange the order of the derivative and the integral (which we can for analytic functions), we have
![\begin{equation*}
\begin{split}
\mathbb{E}_{\theta}[U(X, \theta)] &= \frac{\partial}{\partial \theta} \int f(x; \theta) \ dx \\
&= \frac{\partial}{\partial \theta} \big( 1 \big) \\
&= 0
\end{split}
\end{equation*}](../../assets/latex/probability_and_statistics_e875f5d9ee6249a92e736ef5d54ef78f91fa04d6.png)
For the variance, we can differentiate the above identity:
![\begin{equation*}
\begin{split}
0 &= \frac{\partial}{\partial \theta} \mathbb{E}_{\theta}[U] \\
&= \frac{\partial}{\partial \theta} \int U(x, \theta) f(x \mid \theta) \ dx \\
&= \int U'(x, \theta) f(x \mid \theta) + U(x, \theta) \Big( \frac{\partial}{\partial \theta} f(x \mid \theta) \Big) \ dx \\
&= \int U'(x, \theta) f(x \mid \theta) \ dx + \int U(x, \theta) \Big( U(x, \theta) f(x \mid \theta) \Big) \ dx \\
&= \int U'(x, \theta) f(x \mid \theta) \ dx + \int U^2 f(x \mid \theta) \ dx \\
&= \mathbb{E}_{\theta}[U'] + \mathbb{E}_{\theta}[U^2] \\
&= \mathbb{E}_{\theta}[U'] + \text{Var}_{\theta}(U^2)
\end{split}
\end{equation*}](../../assets/latex/probability_and_statistics_0c91422235ea46c6b9b99425dbd18573eb2ecebd.png)
where we've used the fact that
 and
and ![$\mathbb{E}_{\theta}[U] = 0$](../../assets/latex/probability_and_statistics_01a6c4156e5615ab2aa85e4d2d4df02bc654b0f5.png) , which implies that
, which implies that ![$\text{Var}_{\theta}(U) = \mathbb{E}_{\theta}[U^2]$](../../assets/latex/probability_and_statistics_a5e3956f996d406f4942a9948347f460d0275fcb.png) .
.
This is equivalent to
![\begin{equation*}
\text{Var}_{\theta}(U^2) = - \mathbb{E}_{\theta}[U']
\end{equation*}](../../assets/latex/probability_and_statistics_dfafe59504c65eb46349a7c5653e73f1b550e663.png)
as wanted.
- Asymptotic behavior
Now, since
 maximizes
maximizes  , we must have
, we must have 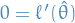 .
.
Consistency of
 ensures that
ensures that  is close to
is close to  (for large n, with high probability). Thus, we an apply first-order Taylor expansion to the equation
(for large n, with high probability). Thus, we an apply first-order Taylor expansion to the equation 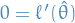 about the point
about the point 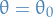 :
:

Thus,
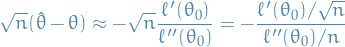
For the denominator, we rewrite as
![\begin{equation*}
\begin{split}
\frac{1}{n} \ell''(\theta_0) &= \frac{1}{n} \sum_{i=1}^{n} \frac{\partial^2}{\partial \theta^2} \Big[ \log f(X_i \mid \theta) \Big]_{\theta = \theta_0} \\
&= \sum_{i=1}^{n} U'(X_i, \theta_0)
\end{split}
\end{equation*}](../../assets/latex/probability_and_statistics_3b26ab2d3e5b7f61665190bffbd702825448448f.png)
and then, by the Law of Large Numbers again, we have
![\begin{equation*}
\sum_{i=1}^{n} U'(X_i, \theta_0) \overset{p}{\to} \mathbb{E}_{\theta_0}[U(X, \theta_0)] = - I(\theta_0)
\end{equation*}](../../assets/latex/probability_and_statistics_4efb018bcb2e4d08fdd85c272f40a87792a9d62c.png)
in probability.
For the numerator, due to what we showed earlier, we know that
![\begin{equation*}
X \sim f(x \mid \theta_0) \quad \implies \quad \mathbb{E}[U] = 0, \quad \text{Var}(U) = I(\theta_0)
\end{equation*}](../../assets/latex/probability_and_statistics_702e14957e619980fa6331a042dedc46b6e84c37.png)
We then have,
![\begin{equation*}
\frac{1}{\sqrt{n}} \ell'(\theta_0) = \frac{1}{\sqrt{n}} \sum_{i=1}^{n} \frac{\partial}{\partial \theta} \Big[ \log f(X_i \mid \theta) \Big]_{\theta = \theta_0} = \frac{1}{\sqrt{n}} \sum_{i=1}^{n} U(X_i, \theta_0)
\end{equation*}](../../assets/latex/probability_and_statistics_8542632ebec3a8e381e6fdaf9ab23585aa75f4be.png)
and by the Central Limit Theorem, we have
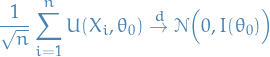
Finally, by Continuous Mapping Theorem and Slutsky's Lemma, we have

- Consistency of
Score test
For a random sample  the total score
the total score
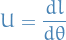
is the sum of  i.i.d. random variables. Thus, by the central limit theorem, it follows that as
i.i.d. random variables. Thus, by the central limit theorem, it follows that as 
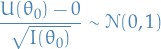
and
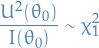
This can then be used as an asymptotic test of the null-hypothesis  .
.
Reject null-hypothesis  if
if

for a suitable critical value  . OR equivalently,
. OR equivalently,
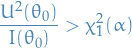
Likelihood Ratio Tests
We expand the log-likelihood using Taylor expansion about the true parameter 
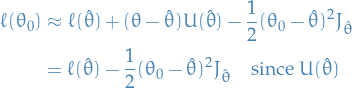
Subtracting  from both sides, and arranging
from both sides, and arranging
![\begin{equation*}
- 2[ \ell(\theta_0) - \ell(\hat{\theta}) ] \approx (\hat{\theta} - \theta_0)^2 J_{\hat{\theta}}
\end{equation*}](../../assets/latex/probability_and_statistics_5c7cbdd5c89c21cdc3832d688f1434cb636fe8a8.png)
And since  , we get
, we get
![\begin{equation*}
- 2[ \ell(\theta_0) - \ell(\hat{\theta}) ] \approx (\hat{\theta} - \theta_0)^2 I_{\theta_0}
\end{equation*}](../../assets/latex/probability_and_statistics_b1dbfc46182b20e94478eca536f288c872cfbccc.png)
which means that the difference between the log-likelihoods can be considered to be a random variable drawn from a  distribution
distribution
![\begin{equation*}
- 2[ \ell(\theta_0) - \ell(\hat{\theta}) ] \sim \chi^2_1
\end{equation*}](../../assets/latex/probability_and_statistics_5dbd5367f5d402842636baff39ffdb78ee7adac0.png)
and we define the term of the left side as the likelihood-ratio .
The test which rejects the  if
if
![\begin{equation*}
- 2[ \ell(\theta_0) - \ell(\hat{\theta}) ] > \chi^2_1(\alpha)
\end{equation*}](../../assets/latex/probability_and_statistics_0245a1e04db8336cd035f789881137590481e0c4.png)
for a suitable significance / critical value  .
.
The above is just saying that we reject the null hypothesis that  if the left term is not drawn from a chi-squared distribution .
if the left term is not drawn from a chi-squared distribution .
Wald test
We test whether or not

That is, we reject the null-hypothesis  if
if

for some suitable signifiance / critical value  .
.
Generalization to multi-parameter case
Hypothesis tests
![\begin{equation*}
\begin{split}
\text{Likelihood ratio test} \quad & -2 [\ell (\boldsymbol{\theta}_0) - \ell( \hat{\boldsymbol{\theta}} )] > \chi_p^2(\alpha) \\
\text{Score test} \quad & U'(\boldsymbol{\theta}_0) I^{-1} (\boldsymbol{\theta}_0) U(\boldsymbol{\theta}_0) > \chi_p^2(\alpha) \\
\text{Wald test (ML test)} \quad & (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0)' I(\boldsymbol{\theta}_0) (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}_0) > \chi_p^2(\alpha)
\end{split}
\end{equation*}](../../assets/latex/probability_and_statistics_f9ff85066fe9b00b1489474d603bf6c092cc7c9e.png)
Confidence regions
![\begin{equation*}
\begin{split}
\text{Likelihood ratio} \quad & \{ \boldsymbol{\theta}: -2 [\ell(\boldsymbol{\theta}) - \ell (\hat{\boldsymbol{\theta}} ) ] < \chi_p^2(\alpha) \} \\
\text{Score} \quad & \{ \boldsymbol{\theta}: U'(\boldsymbol{\theta})I^{-1}(\boldsymbol{\theta}) U(\boldsymbol{\theta}) < \chi_p^2(\alpha) \} \\
\text{Wald (ML)} \quad & \{ \boldsymbol{\theta}: (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta})' I(\boldsymbol{\theta}) (\hat{\boldsymbol{\theta}} - \boldsymbol{\theta}) \chi_p^2(\alpha) \}
\end{split}
\end{equation*}](../../assets/latex/probability_and_statistics_3fd3a827442e46511926ebf2db6f43c8ab7906b7.png)
Likelihood test for composite hypothesis
Let  denote the whole parameter space (e.g.
denote the whole parameter space (e.g.  ). In general terms we have
). In general terms we have
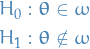
where  .
.
The general likelihood ratio test compares the maximum likelihood attainable if  is restricted to lie in the restricted subspace
is restricted to lie in the restricted subspace  (i.e. under 'reduced' model) with maximum likelihood attainable if
(i.e. under 'reduced' model) with maximum likelihood attainable if  is unrestricted (i.e. under 'full' model):
is unrestricted (i.e. under 'full' model):
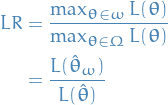
where  is the unrestricted MLE of
is the unrestricted MLE of  and
and  is the restricted MLE of
is the restricted MLE of  .
.
Some authors define the general likelihood ratio test with the numerator and denominator swapped; but it doesn't matter.
Iterative methods

![\begin{equation*}
\boldsymbol{\theta}_{r + 1} = \boldsymbol{\theta}_r - \Bigg( \mathbb{E} \Big[ H(\boldsymbol{\theta}_r) \Big] \Bigg)^{-1} U(\boldsymbol{\theta}_r) = \boldsymbol{\theta}_r + I^{-1}(\boldsymbol{\theta}_r) U(\boldsymbol{\theta}_r)
\end{equation*}](../../assets/latex/probability_and_statistics_a0c9ffa878d32c23912bfdc09a4b75d712023ef0.png)
Simple Linear Regression (Statistical Methodology stuff)
Correlation coefficient and coefficent of determination
The (Pearson) correlation coefficient is given by

and coefficient of determination
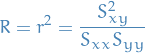
Least squares estimates

Residual sum of squares
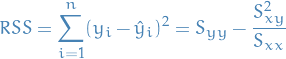
with the estimated standard deviation being
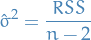
Laplace Approximation
Overview
Under certain regularity conditions, we can approximate a posterior pdf / pmf as a Normal distribution, that is
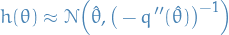
where
 i.e. the log-pdf, with
i.e. the log-pdf, with  being the second-order derivative wrt.
being the second-order derivative wrt. 
 is the posterior we want to approximate
is the posterior we want to approximate
"Derivation"
For any pdf that is smooth and well peaked around its point of maxima, we can use the Laplace approximation to approximate a posterior distribution by a Gaussian pdf.
It follows from taking the second-order Taylor expansion on the logarithm of the pdf.
Let  denote the point of maxima of a pdf
denote the point of maxima of a pdf  , then it also the point of maximia of the log-pdf
, then it also the point of maximia of the log-pdf  and we can write
and we can write
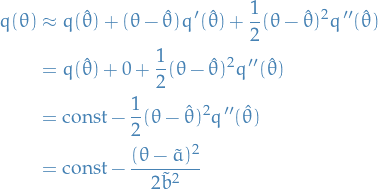
where in the second step we've used the fact that  since
since  is a maxima, and finally let
is a maxima, and finally let

(notice that  since
since  is a maxima )
is a maxima )
But the above is simply the log-pdf of a  , hence the pdf
, hence the pdf  is approx. normal.
is approx. normal.
Hence, if we can find the  and compute the second-order derivative
and compute the second-order derivative  of the log-pdf, we can use Laplace approximation.
of the log-pdf, we can use Laplace approximation.
Guarantees
Consider the model  ,
,  .
.
Under some regularity conditions on the pdfs/pmfs  , including all of the have the same "support", and that for each
, including all of the have the same "support", and that for each  ,
, 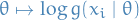 is twice continuously differentiable, we have that for any prior
is twice continuously differentiable, we have that for any prior  which is positive, bounded and twice differentiable over
which is positive, bounded and twice differentiable over  (the parameter space),
(the parameter space),

for large  .
.
Under the same regularity conditions it turns out that  and that
and that  .
.
Point estimators
Notation
 denotes a sufficient statistic
denotes a sufficient statistic
Cramér-Rao lower bound
Notation
Theorem
To state the Cramér-Rao inequality, we need to establish some regularity conditions:
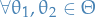 such that
such that  we have
we have  , called identifiability
, called identifiability we have
we have 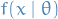 have common support
have common support is an open set
is an open set exists
exists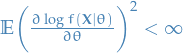
Where we remember that  is the Fisher's information.
is the Fisher's information.
Let  denote a random sample from
denote a random sample from 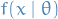 and suppose that
and suppose that  is an estimator of
is an estimator of  . Then, subject to the above regularity conditions,
. Then, subject to the above regularity conditions,
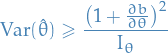
where
![\begin{equation*}
b(\theta) = \text{bias}(\hat{\theta}) \quad \text{and} \quad I_\theta = \mathbb{E} \Bigg[ \bigg( \frac{\partial \ell}{\partial \theta} \bigg)^2 \Bigg]
\end{equation*}](../../assets/latex/probability_and_statistics_2882641d26cffdddf38d341239d881241fcbbd72.png)
- For unbiased
 , the lower bound simplies to
, the lower bound simplies to 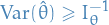
- Regularity conditions are needed to change the order of differentation and integration in the proof given below.
- Proof is for continuous r.v.s, but there is a similar proof for discrete r.v.s.
![\begin{equation*}
\begin{split}
\mathbb{E}[\hat{\theta}] &= \int \dots \int \hat{\theta}(x_1, \dots, x_n) \bigg( \prod_{i = 1}^n f(x_i \mid \theta) \bigg) \ d \mathbf{x} \\
&= \int \dots \int \hat{\theta}(x_1, \dots, x_n) L(\theta; \mathbf{x}) \ d \mathbf{x}
\end{split}
\end{equation*}](../../assets/latex/probability_and_statistics_413cfe281638ca92f751ea0c6096f1c2aea7d5f1.png)
From the definition of bias we have
![\begin{equation*}
\theta + b = \mathbb{E} [ \hat{\theta}] = \int \dots \int \hat{\theta} L(\theta; \mathbf{x}) \ d \mathbf{x}
\end{equation*}](../../assets/latex/probability_and_statistics_25bd1be1d6a6d32f84ca108253645641922184c6.png)
Differentiating both sides wrt.  gives (using the regularity conditions)
gives (using the regularity conditions)

since  does not depend on
does not depend on  . Since
. Since  we have
we have

Thus,
![\begin{equation*}
1 + \frac{\partial b}{\partial \theta} = \int \dots \int \hat{\theta} \frac{\partial l}{\partial \theta} \ L \ d \mathbf{x} = \mathbb{E} \Bigg[ \hat{\theta} \frac{\partial l}{\partial \theta} \Bigg]
\end{equation*}](../../assets/latex/probability_and_statistics_274af0cfd175524bd13828d3896acee0f78d8ce4.png)
Now use the result that for any two r.v.s  and
and  ,
,

and let
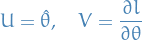
Then
![\begin{equation*}
\begin{split}
\mathbb{E}[V] &= \int \dots \int \frac{\partial l}{\partial \theta} \ L \ d \mathbf{x} = \int \dots \int \frac{\partial L}{\partial \theta} \ d \mathbf{x} \\
&= \frac{\partial}{\partial \theta} \Bigg( \int \dots \int L \ d \mathbf{x} \Bigg) \quad \text{(using regularity conditions)} \\
&= \frac{\partial}{\partial \theta} 1 = 0
\end{split}
\end{equation*}](../../assets/latex/probability_and_statistics_46cfa7730829a4f18a00d645c038263a19b5e10b.png)
Hence
![\begin{equation*}
\text{Cov}(U, V) = \mathbb{E}[UV] = 1 + \frac{\partial b}{\partial \theta}
\end{equation*}](../../assets/latex/probability_and_statistics_9bf1a358b0d4be6efa0580da1e2c7c35a2374609.png)
Similiarily
![\begin{equation*}
\text{Var}(V) = \mathbb{E}[V^2] = \mathbb{E} \Bigg[ \bigg( \frac{\partial l}{\partial \theta} \bigg)^2 \Bigg] = I_\theta
\end{equation*}](../../assets/latex/probability_and_statistics_182ccac28f757f41804ad6d0040e592a6db65b35.png)
and since

we obtain the Cramér-Rao lower bound as
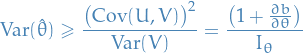
The Cramér-Rao lower bound will only be useful if it is attainable or at least nearly attainable.
Rao-Blackwell Theorem
Theorem
Let  be a random sample of observations from a distribution with p.d.f.
be a random sample of observations from a distribution with p.d.f.  . Suppose that
. Suppose that  is a sufficient statistic for
is a sufficient statistic for  and
and  is any unbiased estimator for
is any unbiased estimator for  .
.
Define ![$\hat{\theta}_S = \mathbb{E}[ \hat{\theta} \mid S]$](../../assets/latex/probability_and_statistics_f67e8f86c468434c61e93025bb60d4882582973e.png) . Then,
. Then,
 is a function of
is a function of  only
only![$\mathbb{E}[\hat{\theta}_S] = \theta$](../../assets/latex/probability_and_statistics_531c30ec2d7161de74437a71e92d7268ca95e4d2.png)

Non-parametric statistics
Maximum Mean Discrepancy (MMD)
Let  be a class of functions
be a class of functions  and let:
and let:
 be Borel probability measures
be Borel probability measures and
and  are i.i.d. observations from
are i.i.d. observations from  and
and  , respectively
, respectively
We define the maximum mean discrepancy (MMD) as
![\begin{equation*}
\text{MMD}[ \mathcal{F}, p, q] := \sup_{f \in \mathcal{F}} \big( \mathbb{E}_x \big[ f(x) \big] - \mathbb{E}_{y} \big[ f(y) \big] \big)
\end{equation*}](../../assets/latex/probability_and_statistics_1c2a4d418cf3881d31e50de49765a5ef062d811e.png)
In the statistics literature, this is an instance of a integral probability metric.
A biased empirical estimate of the  is obtained by replacing the population expectations with empirical expectations computed on the samples
is obtained by replacing the population expectations with empirical expectations computed on the samples  and
and  :
:
![\begin{equation*}
\text{MMD}_b[\mathcal{F}, X, Y] := \sup_{f \in \mathcal{F}} \bigg( \frac{1}{m} \sum_{i=1}^{m} f(x_i) - \frac{1}{n} \sum_{i=1}^{n} f(y_i) \bigg)
\end{equation*}](../../assets/latex/probability_and_statistics_d53ba6e3081c1debe50d59fce58f93002bc2518c.png)
We must therefore identify a function class that is rich enough to uniquely identify whether 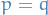 , yet restrictive enough to provide useful finite sample estimates.
, yet restrictive enough to provide useful finite sample estimates.
A RKHS  is characteristic if
is characteristic if

Wavelets
The problem with Fourier transform is that, even though we can extract the frequencies, we do not know at which time these frequencies occurr. This can be incredibly important in cases where the signal has "switches".
Idea is to
- Start with low frequency / high wavelength
- Slide over signal to extract low frequency
- Subtract high frequency away from signal
- Take higher frequency / smaller wavelength
- Slide over signal to extract higher frequency
By subtracting the low frequency we're removing the overlap of the low frequency and high frequency without interferring with the high frequency signal! Thus it's possible to extract both low and high frequencies.
A mother wavelet is some function  such that we can scale and translate to create new wavelets
such that we can scale and translate to create new wavelets 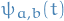 :
:
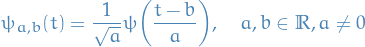
where
 is scaling
is scaling is translation
is translation
And the Fourier transform is then

The condition required by a wavelet on  is that:
is that:

Continuous Wavelet Transform
Wavelet basis
A mother wavelet 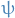 is such that
is such that  form an orthogonal basis for some subspace of
form an orthogonal basis for some subspace of  , hence
, hence
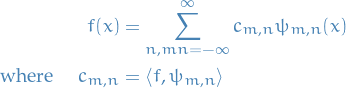
converges to  in the
in the  norm!
norm!
Multi-Resolution Analysis (MRA)
- Overview
- Algorithm for constructing the different resolutions
We consider wavelets
 constructed from some mother wavelet
constructed from some mother wavelet  :
:

and we want to expand our signal in such a wavelet basis.
Consider sequence of subspaces

in
 , with the follow properties:
, with the follow properties:
Nested

Union

is dense in

Orthogonality
Increased "resolution"

 such that
such that  is an orthogonal basis in
is an orthogonal basis in 
 is called the scaling function or father wavelet
is called the scaling function or father wavelet
Let
 be the "standard" scale where our mother wavelet
be the "standard" scale where our mother wavelet 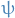 and father wavelet
and father wavelet  live, i.e.
live, i.e.  is
is  for
for  .
.
We can map
 to
to  by
by
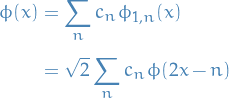
which is called the dilation or two-scale or refinement equation.
We can repeat this argument for arbitrary
 , so with
, so with  , we write
, we write
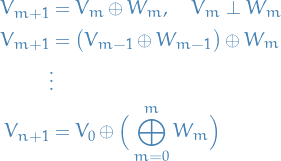
Then,

which means
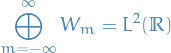
Finally, this tells us that
 (the mother wavelet) such that
(the mother wavelet) such that

constitutes an orthogonal basis for
 .
.
If
 is a multi-resolution analysis (MRA) with scaling function
is a multi-resolution analysis (MRA) with scaling function  , then there exists a mother wavelet
, then there exists a mother wavelet 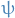 defined
defined
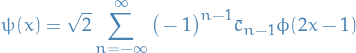
where
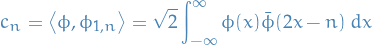
which allows us to obtain an orthormal basis
 for
for  which is dense in
which is dense in  :
:

Application
For more information about how and when to apply wavelet transforms, and which mother wavelet to use, e.g., checkout MATLABs documentation on this.
Testing
Notation
 and
and  denotes the acceptance and critical region, respectively
denotes the acceptance and critical region, respectively denotes the critical value of some statistic
denotes the critical value of some statistic 
Critical region with a given significane level
 is denoted
is denoted

Type I error: Reject
 when
when  is true with
is true with
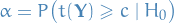
Type II error : Fail to reject
 when
when  is false (equiv., we accept
is false (equiv., we accept  when we shouldn't):
when we shouldn't):

 denotes the test function:
denotes the test function:
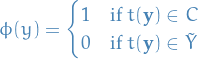
![$\mathbb{E}_{\theta} \left[ \phi(\mathbf{Y}) \right] = \mathbb{E} \left[ \phi(\mathbf{Y}) \mid \theta \right] = \mathbb{E}_{p_{\theta}} \left[ \phi(\mathbf{Y}) \right]$](../../assets/latex/probability_and_statistics_2b92c073cbdab179d6672b96fa8688a5fe0ecf71.png) refers to the expectation over whatever parametrized distribution
refers to the expectation over whatever parametrized distribution  which given you're parametrizing the distribution with
which given you're parametrizing the distribution with  .
.
Definitions
A hypothesis is simple if it defines  completely:
completely:

otherwise, it's composite.
If  is parametric with more than one parameter, a composite hypothesis might specify values of some or all of them (e.g. on regression coefficient).
is parametric with more than one parameter, a composite hypothesis might specify values of some or all of them (e.g. on regression coefficient).
A U-statistic is the class of unbiased statistics; this class arise naturally in producing minimum-variance unbiased estimators (MVUEs)
Important: in statistics there are TWO notions for a U-statistic
Nonparametric statistics is the branch of statistics that is not based solely on parametrized families of probability distributions.
Thus, nonparametric tests or distribution-free tests are procedures for hypothesis testing which, unlike parametric statistics, make no assumptions about the probability distributions of the variables being assessed.
Let the data  and we wish to test two simply hypotheses:
and we wish to test two simply hypotheses:

Suppose that we choose a test statistic  and reject
and reject  if
if 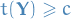 for some critical value
for some critical value  .
.
This induces a partition of the sample space  into two disjoint regions:
into two disjoint regions:
the rejection region
 :
:

the acceptance region
 :
:

We will also sometimes use the notation  to denote the critical region which has the property
to denote the critical region which has the property

Consider  and
and  with corresponding p.d.f.'s
with corresponding p.d.f.'s  ,
,  for
for  .
.
For these hypotheses, comparison between the critical regions of different tests is in terms of
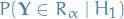
the power of a size  critical region
critical region  for alternative
for alternative  .
.
A best critical region is then the critical region with maximum power.
There are two possible types of error:
- Type I error: Reject
 when
when  is true
is true - Type II error: Fail to reject
 when
when  is false
is false  denotes the probability of Type I error and is called the significance level (or size ) of the test
denotes the probability of Type I error and is called the significance level (or size ) of the test denotes the probability of Type II error which is uniquely defined only if
denotes the probability of Type II error which is uniquely defined only if  is simple, in which case
is simple, in which case
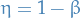
denotes the power of the test. For composite
 ,
,  is the power function.
is the power function.
We can define the test function 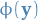 such that
such that
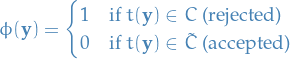
which has the property that
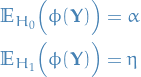
For discrete distributions, the probabilty that the test statistic lies on the boundary of the critical region,  , may be non-zero.
, may be non-zero.
In that case, it is sometimes necessary to use a randomized test, for which the test function is
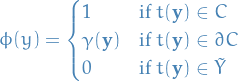
for some function 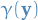 and we reject
and we reject  based on observed data
based on observed data  with probability
with probability 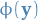 .
.
Suppose now there is a parametric family 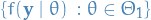 of alternative p.d.f.'s for
of alternative p.d.f.'s for  .
.
The power of a size  critical region
critical region  generalizes to the size
generalizes to the size  power function
power function
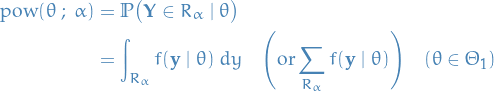
A size  critical region
critical region  , is then uniformly most powerful size
, is then uniformly most powerful size  (UMP size
(UMP size  ) if it has maximum power uniformly over
) if it has maximum power uniformly over  (
( is NOT power,
is NOT power,  is).
is).
A test is UMP if all its critical regions are UMP, or more formally:
A uniformly most powerful or UMP test,  , of size
, of size  is a test
is a test  for which
for which
![$\mathbb{E}_{\theta} \big[ \phi_0 (\mathbf{Y}) \big] \le \alpha, \quad \forall \theta \in \Theta_0$](../../assets/latex/probability_and_statistics_5dfdf67d44e008fef120cd0327b3d78ab866fd18.png)
Given any other test
 for which
for which ![$\mathbb{E}_{\theta} \big[ \phi(\mathbf{Y}) \big] \le \alpha$](../../assets/latex/probability_and_statistics_84c4722f199becaa365cdb7e1734b2da36204336.png) for all
for all  , we have
, we have
![\begin{equation*}
\mathbb{E}_{\theta} \big[ \phi_0(\mathbf{Y}) \big] \ge \mathbb{E}_{\theta} \big[ \phi(\mathbf{Y}) \big], \quad \forall \theta \in \Theta_1
\end{equation*}](../../assets/latex/probability_and_statistics_8f438aa7ce8238487ad5d1e0f204afc7a13eca22.png)
i.e. expectation given
 is at least as large as for the less powerful statistic (who's test function is
is at least as large as for the less powerful statistic (who's test function is  ).
).
A test 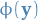 of
of 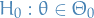 against
against  is called unbiased of size
is called unbiased of size  if
if
![\begin{equation*}
\sup_{\theta \in \Theta_0} \mathbb{E} \left[ \phi(\mathbf{Y}) \mid \theta \right] \le \alpha
\end{equation*}](../../assets/latex/probability_and_statistics_f358da7a1208c38085dbfe718ebd698fc6466ea1.png)
and
![\begin{equation*}
\mathbb{E} \left[ \phi(\mathbf{Y}) \mid \theta \right] \ge \alpha, \quad \forall \theta \in \Theta_1
\end{equation*}](../../assets/latex/probability_and_statistics_9a79a49bf61bb7bc24f9d9a25c60f749b094d886.png)
Informally, unbiased test is one which has higher probability of rejecting  when it is false, than when it is true.
when it is false, than when it is true.
A test which is uniformly most powerful among the set of all unbiased tests is called the uniformly most powerful unbiased (UMPU).
Two-sample test
The problem of comparing samples from two probability distributions, by a statistical tests of the null hypothesis that these distributions are equal against the alternative hypothesis that these distributions are different (this is called the two-sample problem), i.e. in short:
 corresponds to distributions being equal
corresponds to distributions being equal corresponds to distributions being different
corresponds to distributions being different
Exact test
A test is exact if and only if

which is in contrast to non-exact tests which only have the property

for some "critical constant"  .
.
Hypothesis testing
For any size  , the LR critical region is the best critical region for testing simple hypothesis
, the LR critical region is the best critical region for testing simple hypothesis  vs.
vs.  .
.
That is, suppose one is performing a hypothesis test between two simple hypothesis  and
and 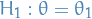 , using the likelihood-ratio test with threshold
, using the likelihood-ratio test with threshold  which rejects
which rejects  in favour of
in favour of  at a significance level of
at a significance level of

where
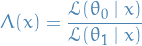
Then,  is the most powerful test at significance level
is the most powerful test at significance level  .
.
Bahadur efficiency
Most of this stuff is from https://www.encyclopediaofmath.org/index.php/Bahadur_efficiency.
Notation
 and
and  denotes the null hypothesis and the alternative hypothesis
denotes the null hypothesis and the alternative hypothesis and
and  are the parametric set corresponding to the
are the parametric set corresponding to the  and
and  , respectively
, respectively- A test statistic
 based on a random sample
based on a random sample 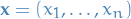



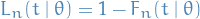
 -value refers to the minimum value we require from the test for us to accept
-value refers to the minimum value we require from the test for us to accept 
 is the information number corresponding to
is the information number corresponding to  and
and 
Stuff
- Assume large values of
 give evidence against
give evidence against 
- For fixed
 and a real number
and a real number  let
let
Random quantity

is the  value corresponding to the statistic
value corresponding to the statistic  when
when  is the true parametric value.
is the true parametric value.
For example, if

and the null hypothesis  is rejected at the significance level
is rejected at the significance level  .
.
If for  with
with  probability one we will have
probability one we will have

then  is called the Bahadur exact slope of
is called the Bahadur exact slope of  .
.
The larger the Bahadur exact slope , the faster the rate of decay of the  value under the alternative. It is known that for any
value under the alternative. It is known that for any  ,
,  where
where  is the information number corresponding to
is the information number corresponding to  and
and  .
.
A test statistic  is called Bahadur efficient at
is called Bahadur efficient at  if
if

Bahadur efficiency allows one to compare two (sequences of) test statistics  and
and  from the following perspective:
from the following perspective:
Let  be the smallest sample size required to reject
be the smallest sample size required to reject  at the significance level
at the significance level  on the basis of a random sample
on the basis of a random sample  when
when  is the true parametric value.
is the true parametric value.
The ratio  gives a measure of relative efficiency of
gives a measure of relative efficiency of  to
to  .
.
To reduce the number of arguments,  ,
,  and
and  , one usually considers the rv. which is the limit of this ratio, as
, one usually considers the rv. which is the limit of this ratio, as  . In many situations this limit does not depend on
. In many situations this limit does not depend on  , so it represents the efficiency of
, so it represents the efficiency of  against
against  at
at  with the convenient formula
with the convenient formula
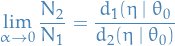
where  and
and 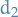 are the corresponding Bahadur slopes.
are the corresponding Bahadur slopes.
I.e. can use the Bahadur efficiency to compare the number of samples needed to reject  .
.
Kolmogorov-Smirnov
The empirical distribution function is given by
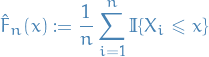
Consistency and unbiasedness at a point
Fix  , then
, then

Consequently,
![\begin{equation*}
\mathbb{E} \big[ \hat{F}_n(x) \big] = \frac{1}{n} \mathbb{E} \big[ n \hat{F}_n(x) \big] = F(x)
\end{equation*}](../../assets/latex/probability_and_statistics_686c616974b5a3a767898c5ae985b63349323e0a.png)
That is,  is an unbiased estimator of
is an unbiased estimator of  for each fixed 4x$. Also
for each fixed 4x$. Also
![\begin{equation*}
\text{Var}\big( \hat{F}_n(x) \big) = \frac{1}{n^2} \text{Var} \big( n \hat{F}_n(x) \big) = \frac{F(x) [1 - F(x)]}{n}
\end{equation*}](../../assets/latex/probability_and_statistics_a8ae67fb0ede2e48c804746e4caa4f3ae06a7313.png)
Consequently, by the Chebyshev inequality,

Therefore,  is consistent
is consistent
Kolmogorov-Smirnov test
The Kolmogorov distribution is the distribution of the rv.
![\begin{equation*}
K = \sup_{t \in [0, 1]} |B(t)|
\end{equation*}](../../assets/latex/probability_and_statistics_75ce76d3d234d22476784fb3c5a98f3340ccd722.png)
where  is the Brownian bridge. The cumulative distribution function of
is the Brownian bridge. The cumulative distribution function of  is given by
is given by
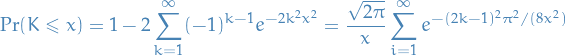
The empirical distribution function  for i.i.d. observations
for i.i.d. observations 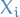 is defined as
is defined as
![\begin{equation*}
F_n(x) = \frac{1}{n} \sum_{i = 1}^{n} I_{[- \infty, x]} (X_i)
\end{equation*}](../../assets/latex/probability_and_statistics_03be4b965828593bd5e630c5fca6943a50d56b07.png)
where
![$I_{[-\infty, x]}(X_i)$](../../assets/latex/probability_and_statistics_3dc038ff7fbccbf9dd8f92d3b652bd55aeca1992.png) is the indicatior function defined
is the indicatior function defined
![\begin{equation*}
I_{[-\infty, x]}(X_i) =
\begin{cases}
1 & \text{if } X_i \le x \\
0 & \text{otherwise}
\end{cases}
\end{equation*}](../../assets/latex/probability_and_statistics_89de4fd4d6eb8e6f7e0cf66ee19ddcf422f9b76d.png)
The Kolmogorov-Smirnov statistic for a given cumulative distribution function  is
is

Under  that the sample comes from the hypothesized distribution
that the sample comes from the hypothesized distribution 
![\begin{equation*}
\sqrt{n} D_n \overset{n \to \infty}{\longrightarrow} \sup_{t \in [0, 1]} | B (t) |
\end{equation*}](../../assets/latex/probability_and_statistics_208b3e9335425438be555fd5d3abd40cd5f8a1dc.png)
in distribution, where  is the Brownian bridge.
is the Brownian bridge.
If  is continuous, then under
is continuous, then under 
 converges to the Kolmogorov distribution, which does not depend on
converges to the Kolmogorov distribution, which does not depend on  .
.
Kolmogorov-Smirnov test (K-S test) is a non-parametric test of the equality of continuous , one-dimensional probability distributions that can be used to compare one sample with a reference probability distribution (one-sample K-S test ), or to compare two samples (two-sample K-S test).
The one-sample KS test is:
Using critical values of the Kolmogorov distribution, where we reject
 at level
at level  if
if

where

F-test
An F-test is any statistical test in which the test statistic, called a F-statistic, has an F-distribution under the null hypothesis.
Residual-sum of squares between two models as a F-statistic
Notation
 denotes the number of samples
denotes the number of samples denotes the number of regressors (including the constant term)
denotes the number of regressors (including the constant term) denotes the number of linear "restrictions" / "constraints", and therefore, also the degrees of freedom
denotes the number of linear "restrictions" / "constraints", and therefore, also the degrees of freedom is
is  matrix with full column rank
matrix with full column rank  , i.e.
, i.e.  , which translates into constraints being "independent". This matrix is used to enforce the constraints on
, which translates into constraints being "independent". This matrix is used to enforce the constraints on  , i.e. if we don't want a constant term / intercept
, i.e. if we don't want a constant term / intercept 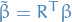 is such that
is such that  , if the constant term was in the first entry.
, if the constant term was in the first entry. represents the hypothesized residual sum
represents the hypothesized residual sum
Stuff
Consider two linear regression models with coefficients  and
and  , with
, with  . Then let
. Then let  and
and  denote the respective number of coefficients, with
denote the respective number of coefficients, with  . Then letting
. Then letting
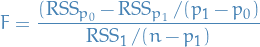
we have

i.e. the quantity above is F-distributed.
Note: observe that  so the above is a positive quantity.
so the above is a positive quantity.
Consider the null-hypothesis  . Recall the OLS solution is given by
. Recall the OLS solution is given by
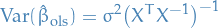
and we therefore have

Let

and let, using Cholesky decomposition,  be such that
be such that

we have a "matrix square root" of  in
in  . The purpose of this matrix is so we can define the following random variable:
. The purpose of this matrix is so we can define the following random variable:

where  denotes the identity
denotes the identity  identity matrix. To see that this is indeed the case, observe that
identity matrix. To see that this is indeed the case, observe that
Using properties seen in the proof of  , know that this
, know that this  is independent of the rv.
is independent of the rv.
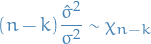
where
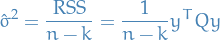
where

known as the residual maker matrix. Then we have
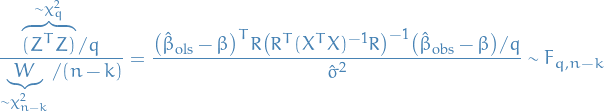
Recall that a F-statistic is a ratio between  divided by their corresponding degrees of freedom, hence the above.
In particular, under
divided by their corresponding degrees of freedom, hence the above.
In particular, under  , this reduces to the statistic
, this reduces to the statistic
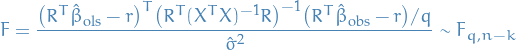
Letting  (which is the number of components of
(which is the number of components of  we set to zero to get
we set to zero to get  ) and
) and 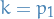 (since this is how many parameters we now have), we conclude our proof.
(since this is how many parameters we now have), we conclude our proof.
Proof that 
Consider the regression model

with
Then the residual vector is estimated by

And is distributed according to
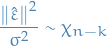
and thus
![\begin{equation*}
\mathbb{E} \big[ \norm{\hat{\varepsilon}}^2 \big] = \sigma^2
\end{equation*}](../../assets/latex/probability_and_statistics_434f1a6ffdbff93d25cd1c541e8e9f3dc9066608.png)
Consider the following linear model

where  ,
,  and
and  .
The vector of residuals is estimated by
.
The vector of residuals is estimated by

where

Since trace is invariant under cyclic permutations, we have

since  matrices, and so
matrices, and so  . Therefore
. Therefore

Futhermore,

which is seen by the fact that
![\begin{equation*}
\begin{split}
Q^2 &= \Big( I - X \big( X^T X \big)^{-1} X^T \Big) \Big( I - X \big( X^T X \big)^{-1} X^T \Big) \\
&= I - X \big( X^T X \big)^{-1} X^T - X \big( X^T X \big)^{-1} X^T + \big[ X \big( X^T X \big)^{-1} \underbrace{X^T X \big( X^T X \big)^{-1}}_{= I} X^T \big] \\
&= I - 2 X \big( X^T X \big)^{-1} X^T + X \big( X^T X \big)^{-1} X^T \\
&= I- X \big( X^T X \big)^{-1} X^T \\
&= Q
\end{split}
\end{equation*}](../../assets/latex/probability_and_statistics_c7a8f5617d17a9e436e43601b88ac14a36e4171c.png)
We then have the following sequence of implications:


 only has eigenvalues
only has eigenvalues  and
and 

 is normal and so there exists a unitary matrix
is normal and so there exists a unitary matrix  such that
such that

Recall that

which is seen by computing ![$\mathbb{E} \big[ \big( V^T \hat{\varepsilon} \big) \big( V^T \hat{\varepsilon} \big)^T \big]$](../../assets/latex/probability_and_statistics_9b5107f237e66df714c82f29f30f146a1a27c740.png) and using
and using ![$\mathbb{E} \big[ \hat{\varepsilon} \hat{\varepsilon}^T \big] = \sigma^2 Q$](../../assets/latex/probability_and_statistics_c425ecd6c327091ca01e027fb7abd92bc8ee8e2a.png) . From this it follows that
. From this it follows that
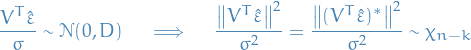
where  is the corresponding
is the corresponding  vector (since the rest of the components have zero variance and thus add nothing to the norm).
vector (since the rest of the components have zero variance and thus add nothing to the norm).
Furthermore, since  is unitary, as mentioned earlier, we have
is unitary, as mentioned earlier, we have
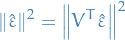
Recall that the residual sum-of-squares is given by  , and so arrive at our result
, and so arrive at our result

Finally, observe that this implies
![\begin{equation*}
\mathbb{E} \big[ \norm{\hat{\varepsilon}}^2 \big] = \sigma^2
\end{equation*}](../../assets/latex/probability_and_statistics_434f1a6ffdbff93d25cd1c541e8e9f3dc9066608.png)
Similarity testing
Notation
 with can take on values
with can take on values 
 denotes a test
denotes a test
Stuff
Test 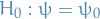 vs.
vs. 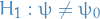 .
.
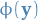 is a test of size
is a test of size  , i.e.
, i.e.
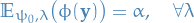
Then  is a similar test of size
is a similar test of size  .
.
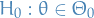 with
with  on the boundary of
on the boundary of  .
.
Confidence regions
Notation
 is drawn from some distribution
is drawn from some distribution


 is a size
is a size  critical region for
critical region for 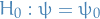

with

- critical region refers to the sampling distribution which will lead to the rejection of the hypothesis tested when the hypothesis is true.
Stuff
- Generalization of confidence intervalls to multiple dimensions
 is a
is a  confidence region for
confidence region for 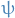 if
if

If  then
then

Pivotal quantities
 which has a distribution independent of
which has a distribution independent of 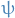 , i.e.
, i.e.  is a pivotal statistic, that is
is a pivotal statistic, that is

Then we can construct a value  such that we obtain a confidence region following:
such that we obtain a confidence region following:

Decision Theory
Notation
 denotes the sample space i.e.
denotes the sample space i.e. 
 denotes the parameter space
denotes the parameter space denotes a family of probability distributions
denotes a family of probability distributions is the action space, i.e. set of actions an experiment can take after observing data, e.g. reject or accept
is the action space, i.e. set of actions an experiment can take after observing data, e.g. reject or accept  , estimating the value of
, estimating the value of  , etc.
, etc. denotes the loss function
denotes the loss function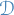 denotes decision rules , with
denotes decision rules , with  is a function
is a function 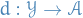 that associates a particular decision which each possible observed data set.
that associates a particular decision which each possible observed data set.
Stuff
For a parameter  , the risk of a decision rule,
, the risk of a decision rule,  , is defined as
, is defined as
![\begin{equation*}
R(\theta, d) = \mathbb{E}_{\theta} \Big[ \big( \theta, d(Y) \big) \Big] =
\begin{cases}
\sum_{y \in \mathcal{Y}} L \Big( \theta, d(y) \Big) f(y ; \ \theta) & \text{for discrete } \mathcal{Y} \\
\int_{\mathcal{Y}} L \Big( \theta, d(y) \Big) f(y ; \ \theta) \ dy & \text{for continuous } \mathcal{Y}
\end{cases}
\end{equation*}](../../assets/latex/probability_and_statistics_b77811a2c9f897a2cf753569e3d6d72260fb7031.png)
In other words, the risk is the expected loss of a particular decision rule  when the true value of the unknown parameter is
when the true value of the unknown parameter is  .
.
Note: this is fundamentally a frequentist concept, since the definition implicitly invokes the idea of repeated samples from the parameter space  and computes the average loss over these hypothetical repetitions.
and computes the average loss over these hypothetical repetitions.
Selection of decision rule
Given two possible decision rules  and
and 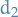 , the rule
, the rule  strictly dominates the rule
strictly dominates the rule 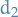 if
if
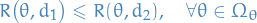
and there exists at least one value of  , e.g. θ', for which
, e.g. θ', for which

It is clear that we would always prefer  to
to  .
.
If, for a given decision rule  , there exists some decision rule
, there exists some decision rule  that strictly dominates
that strictly dominates  , then
, then 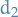 is said to be inadmissible.
is said to be inadmissible.
Conversely, if there is no decision rule that dominates 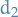 , then
, then 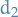 is said to be admissible.
is said to be admissible.
That is, generally less-than-or-equally AND has at least ONE value of  for which we have strict inequality.
for which we have strict inequality.
Unbiasedness
We say a loss-function is unbiased if
![\begin{equation*}
\mathbb{E}_{\theta} \Big[ L \big( \theta', d(Y) \big) \Big] \ge \mathbb{E}_{\theta} \Big[ L(\theta, d(Y) \Big], \quad \forall \theta, \theta' \in \Omega_{\theta}
\end{equation*}](../../assets/latex/probability_and_statistics_1e495084263dfd7cac89cd62e28f348850ddb2c9.png)
i.e. loss of the decision rule should be minimized for the true value of the parameter  .
.
Minimax decision rules
A decision rule is minimax if it minimizes the maximum risk
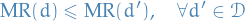
which can also be written

Bayes decision rules
The Bayes risk of a decision rule,  , is defined by
, is defined by
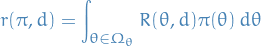
or by a sum in case of discrete-valued probability distribution.
A decision rule is a Bayes rule with respect to the prior  if it minimizes the Bayes risk, i.e.,
if it minimizes the Bayes risk, i.e.,
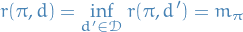
Definition of Bayes risk assumes that the infimum is achieved by some rule, which might not always be true.
In those cases, for any  , we can find a decision rule
, we can find a decision rule  such that
such that

Such a rule is said to be  *Bayes wrt. prior
*Bayes wrt. prior  .
.
A useful choice of prior is the one that is most conservative in its estimate of risk. This gives rise to the concept of a least favourable prior.
We say  is a least favourable prior if, for any other prior
is a least favourable prior if, for any other prior  we have
we have

where  are the Bayes (decision) rules corresponding to
are the Bayes (decision) rules corresponding to  and
and  .
.
Randomized decision rules
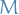 decision rules
decision rules  which we choose from with probabilties
which we choose from with probabilties  , with
, with  and
and 
Define
 to be the rule "selection decision rule
to be the rule "selection decision rule 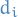 with prob.
with prob.  ", called the randomized decision rule, which has risk
", called the randomized decision rule, which has risk
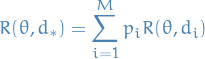
- Sort of a linear combination of decision rules
- Minimax rules are often this way
- Supremum over
 of the risk for
of the risk for 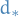 is smaller than the supremum of the risk for any of the decision rules individually
is smaller than the supremum of the risk for any of the decision rules individually
- Supremum over
Finding minimax rules
Suppose that  is a Bayes (decision) rule corresponding to prior
is a Bayes (decision) rule corresponding to prior  and
and  , then
, then
 is a minimax decision rule
is a minimax decision rule is the least favourable prior
is the least favourable prior
Admissibility of Bayes (decision) rules
We have the following three theorems:
Assume that the parameter space, 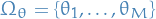 , is finite and a given prior
, is finite and a given prior  gives positive weight to each
gives positive weight to each  .
.
The a Bayes (decision) rule wrt.  is admissible.
is admissible.
If a Bayes (decision) rule is unique, it is admissible.
Let  be a subset of the real line. Assume that hte risk functions
be a subset of the real line. Assume that hte risk functions  are continuous in
are continuous in  for all decision rules
for all decision rules  .
.
If the prior 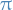 has the property that for any
has the property that for any  and any
and any  , the interval
, the interval  has non-zero probability under
has non-zero probability under  , then the Bayes (decision) rule wrt.
, then the Bayes (decision) rule wrt.  is admissible.
is admissible.
James-Stein Estimators
Notation

 is the square loss function
is the square loss functionRisk of a decision rule is then given
![\begin{equation*}
R\Big( \mu, \hat{\mathbf{d}}^0(\mathbf{Y}) \Big) = \mathbb{E} \Big[ \norm{\mu - \mathbf{Y}} \Big]^2 = \sum_{i=1}^{p} \mathbb{E} \big[ (\mu_i - Y_i)^2 \big] = \sum_{i=1}^{p} \text{Var}(Y_i)
\end{equation*}](../../assets/latex/probability_and_statistics_2e8525d65e4bb539bb0116945f5781cc319156b9.png)
Stein's Paradox
The class of James-Stein estimators of the form
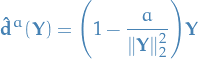
has smaller risks that are also independent of  and hence strictly dominate the natural estimator
and hence strictly dominate the natural estimator

These are called shrinkage estimators as they shrink  towards
towards  when
when 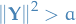 , and has the following consequence: folding in information from variables that are independent of the variable of interest can, on average, improve estimation of the variable of interest!
, and has the following consequence: folding in information from variables that are independent of the variable of interest can, on average, improve estimation of the variable of interest!
Suppose

and  is an almost differentiable function then
is an almost differentiable function then
![\begin{equation*}
\frac{1}{\sigma^2} \mathbb{E} \Big[ (\mathbf{X} - \mu) f(\mathbf{X}) \Big] = \mathbb{E} \Big[ \nabla f(\mathbf{X}) \Big]
\end{equation*}](../../assets/latex/probability_and_statistics_9d084ea14dd7bf28bc5e8f5258a63c239033506e.png)
First we do the univariate case.
Suppose
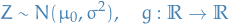
which is absolutely continuous, and
![\begin{equation*}
\mathbb{E} \big[ g'(Z) \big] < \infty
\end{equation*}](../../assets/latex/probability_and_statistics_54d8dd82c3a81f88ffe111bfa400c5e1542d061c.png)
Using change of variables to set 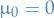 and
and 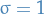 , then
, then  is std. normal. Then
is std. normal. Then
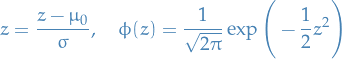
Then one simply substitute into the Stein's lemma and prove that it is indeed satisfied.
Bayesian Statistics
Model comparison
Bayesian Information Criterion (BIC)
Bayesian Information Criterion (BIC) is a criterion for model selection among a finite set of models; the model with the lowest BIC is preferred.
The BIC is defined as:

where
 is the MLE of the model
is the MLE of the model the obsered data
the obsered data is the number of data points in
is the number of data points in 
 is the number of parameters in the model
is the number of parameters in the model
BIC is an asymptotic result derived under the assumptions that the data distribution follows an exponential family.
Limitations:
- Approximation only valid for sample sizes

- The BIC cannot handle complex collections of models as in the variable selection problem in high-dimensions
Akaike Information Criterion (AIC)
- Given collection of models for some data, estimates quality of each model, relative to each of the other models
- NOT a test of model in a sense of testing a null hypothesis, i.e. says nothing about the absolute quality, only relative quality
Suppose we have a statistical model of some data.
Let:
 be the number of estimated parameters in the model
be the number of estimated parameters in the model be the maximum value of the likelihood function for the model
be the maximum value of the likelihood function for the model
Then the Akaike Information Criterion (AIC) value of the model is

Given a set of candidate models for the data, the preferred model is the one with the minimum AIC value.
Thus, AIC rewards goodness-of-fit (as assessed by the likelihood function), but it also penalizes large number of parmateres (complexity).
AIC is based on information theory. Suppose data was generated by some unknown process  , and we're considering two candidate models to
, and we're considering two candidate models to  and
and  . We could then compute the KL-divergence of
. We could then compute the KL-divergence of  and
and  ,
,  , and of
, and of  and
and  ,
,  , i.e. the "loss of information" by representing
, i.e. the "loss of information" by representing  using
using  or
or  , respectively. One could then compare these values, and choose the candidate model which had the smallest KL-divergence with
, respectively. One could then compare these values, and choose the candidate model which had the smallest KL-divergence with  .
.
Asymptotically, making this choice is equivalent of choosing the model  with the smallest
with the smallest
AIC! Note, however, that AIC can be a bad comparison if the number of samples is small.
TODO ANOVA
One-way
Two-way
Bootstrapping
- Bootstrap methods gets its name due to "using data to generate more data" seems analogous to a trick used by the fictional Baron Munchausen, who when he found himself at the bottom of a lake got out by pulling himself up by his bootstraps :)
Notation
 is a single homogenous sample of data with PDF
is a single homogenous sample of data with PDF  and CDF
and CDF 
- Statistic
 whose value in the sample is
whose value in the sample is  , which estimates
, which estimates  , an underlying characterstic of the population. Generally
, an underlying characterstic of the population. Generally  is a symmetric function of
is a symmetric function of 
- EDF stands for the empirical distribution function, denoted

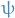 denotes the parameter of a parametric model with CDF and PDF
denotes the parameter of a parametric model with CDF and PDF  and
and  , respectively
, respectively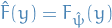 is the fitted model to data drawn from the PDF
is the fitted model to data drawn from the PDF 
 denotes the rv. distributed according to the fitted model, and we do the same for other moments (e.g.
denotes the rv. distributed according to the fitted model, and we do the same for other moments (e.g.  denotes the mean of the fitted model)
denotes the mean of the fitted model) denotes the random variable of the statistic of interested, in comparison to
denotes the random variable of the statistic of interested, in comparison to  which is the observed estimate, or rather
which is the observed estimate, or rather
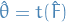
Stuff
- Interested in probability distribution of

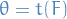 describes the fact that the population parameter
describes the fact that the population parameter  is equal to the value the statistic
is equal to the value the statistic  takes on for the underlying CDF
takes on for the underlying CDF 
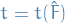 expresses the relationship between the estimate
expresses the relationship between the estimate  and
and 
- To be properly rigorous, we would write
 and require that
and require that  as
as  , possibly even that
, possibly even that 
- We will mostly assume

- To be properly rigorous, we would write
Moment estimates
- Suppose we simulate a dataset
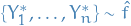 , i.e. from fitted model
, i.e. from fitted model - Properties of
 are then estimated from
are then estimated from  , using
, using  repetitions of the data simulation
repetitions of the data simulation - Important to recognize that we are not estimating absolute properties of
 , but rather of
, but rather of  relative to
relative to 
Distribution and quantile estimates
- Approximating the distribution of
 by that of
by that of 
Cumulative probabilities are estimated by EDF of the simulated values
 , i.e. if
, i.e. if

then the simulation estimate of
 is
is
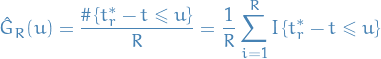
And
 , the exact CDF of
, the exact CDF of  under sampling from the fitted model
under sampling from the fitted model
- Approximation
 to
to  contains two sources of error:
contains two sources of error:
 to
to  due to data variability
due to data variability to
to  due to finite simulation
due to finite simulation
- Quantiles of distribution of

- Approximated using ordered values of

Suppose
 are independent distribution with CDF
are independent distribution with CDF  and if
and if  denotes the j-th ordered value, then
denotes the j-th ordered value, then
![\begin{equation*}
\mathbb{E} \big[ X_{(j)} \big] = K^{-1} \bigg( \frac{j}{N + 1} \bigg)
\end{equation*}](../../assets/latex/probability_and_statistics_eafdc619839199c74413ce20a1ca0690dbedbf83.png)
- This implies a sensible estimate of
 is the
is the  , assuming that
, assuming that  is an integer
is an integer
- Therefore we can estimate
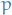 quantile of
quantile of  by the
by the 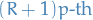 oredered value of
oredered value of  , i.e.
, i.e. 
- We're assuming
 is chosen so that
is chosen so that 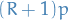 is an integer
is an integer
- Therefore we can estimate
- Approximated using ordered values of
Nonparametric simulation
- Same as in previous section, but EDF to perform simulation instead of estimate of parameter for distribution (e.g. using MLE estimate of
 ); call this nonparametric bootstrap
); call this nonparametric bootstrap
Simple confidence intervals
If we use bootstrap estimates of quantiles for  , then an equitailed
, then an equitailed 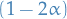 confidence interval will have limits
confidence interval will have limits
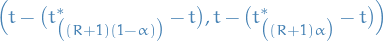
where we explicitly write the second term in the parenthesis in the limits to emphasize that we're looking at  with an expectation
with an expectation  .
.
This is based on the probability implication

Reducing error
- Problem: choose quantity
 such that
such that  is as nearly pivotal as possible
is as nearly pivotal as possible
- That is, it has (at least approx.) the same distribution under sampling from both
 and
and 
- That is, it has (at least approx.) the same distribution under sampling from both
Let
 with
with  increasing in
increasing in  and if
and if  is an approx. lower
is an approx. lower  quantile of
quantile of  , then
, then
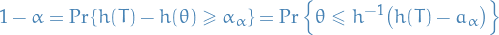
where
 is the inverse transformation
is the inverse transformation
- Thus,
 is an upper
is an upper  confidence limit for
confidence limit for 
So we're basically saying "Let's bound the difference between  of the true
of the true  and
and  of our estimator
of our estimator  by
by  , with a certainty / probability of
, with a certainty / probability of  "
"
OR rather, "let's bound the probability of the difference between  and
and  being
being  "
"
OR "we want some constant  such that the probability of
such that the probability of  and
and  differ by more than
differ by more than  to be bounded by
to be bounded by  ", and we
", and we
Theoretical basis for bootstrap
Suppose we have a random sample  , or equiv., its EDF
, or equiv., its EDF  .
.
We want to estimate some quantity  , e.g.
, e.g.

and want to estimate the distribution function
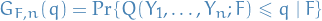
where the conditioning on  indicates that
indicates that  is a random sample from
is a random sample from  .
.
The bootstrap estimate of  is then
is then

where in this case
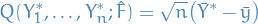
In order for

we need the following conditions to hold (letting  be a neighborhood of
be a neighborhood of  in a space of suitable distributions):
in a space of suitable distributions):
- For any
 ,
,  must converge weakly to a limit
must converge weakly to a limit 
- This convergence must be uniform on

- The function mapping
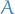 to
to 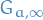 must be continuous
must be continuous
where converge weakly means

for all integrable functions 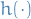 .
.
Under these conditions, the bootstrap estimate is consistent.
Resampling for testing
Nonparametric Permutation tests
- Permutation test is a two-sample test
- Have samples
 and
and  for two distributions.
for two distributions. - Want to check if
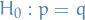 is true
is true Consider some statistic which measure discrepancy between the two sample-sets, e.g. mean difference
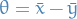
- Under
 , for every sample
, for every sample 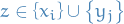 , whether or not the sample came from distribution
, whether or not the sample came from distribution 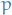 or
or  should be equally likely, since under
should be equally likely, since under  we have
we have 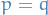
- Therefore we consider consider permutations between the samples form the distributions!
Consider
 tuple
tuple
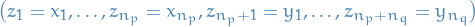
Permute the tuple

where
 is a permutation on
is a permutation on  symbols.
symbols.
- Let
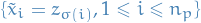 and
and 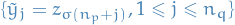
- Compute
 assuming
assuming  to come from
to come from  and
and  to come from
to come from  .
.
Gives us achieved significance level (ASL), also known as the p-value, by considering

i.e. the probability of getting a
 large value when
large value when  is true
is true
- Observe that
 is a "discrepancy" measurement between the samples, e.g. the difference, and so "large values = BAD"
is a "discrepancy" measurement between the samples, e.g. the difference, and so "large values = BAD"
- Observe that
Practically, there can be a lot of permutations to compute; 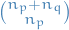 possibilities, in fact. Therefore we estimate the
possibilities, in fact. Therefore we estimate the  by "sampling" permutations uniformly:
by "sampling" permutations uniformly:

where  corresponds to the estimate of
corresponds to the estimate of  using the m-th sampled permutated dataset, and
using the m-th sampled permutated dataset, and  is the number of permutations considered.
is the number of permutations considered.
Note: permutation test is an exact test when all permutations are computed.
Frequentist bootstrapping
- Data approximates unknown distribution
- Sampling distribution of a statistic can be approximated by repeatedly resampling the observations with replacement and computing the statistic for each sample
Let
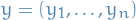 denote the original samples
denote the original samples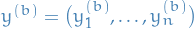 denote the bootstrap sample
denote the bootstrap sample
- Likely have some observations repeated one or more times, while some are absent
Equivalently, we can instead make the following observation:
- Each original observation
 occurs anywhere from
occurs anywhere from  to
to  times
times Let
 denote # of times
denote # of times  occurs in
occurs in  and
and
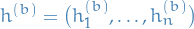
thus
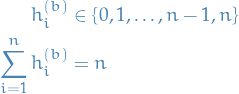
Let
 such that
such that
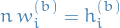
then

- Hence we can compute the bootstrap sample
 by instead drawing
by instead drawing  this way, and weighting the original samples by these drawn weights!
this way, and weighting the original samples by these drawn weights!
Recall that

has the property that
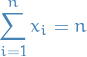
Hence,
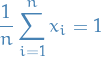
TODO Bayesian bootstrapping
Problems / Examples
Multi-parameter MLE
Normal samples
Suppose we have the samples  following the model
following the model

Then we want to test 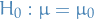 against
against 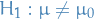 .
.
The likelihood is given by

Under our restricted parameter-space  (
(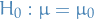 ): then the MLE
): then the MLE
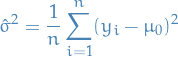
Under  (
( and
and 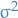 can take on any value):
can take on any value):
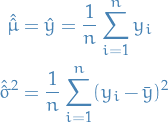
Thus, the likelihood ratio is
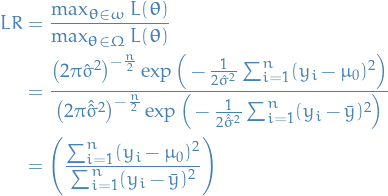
But
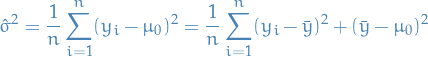
and thus
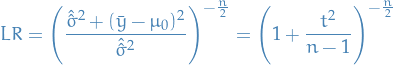
where
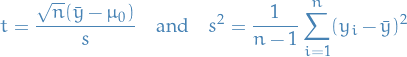
Rejecting for small values for LR is equivalent to rejecting for large values of  , i.e. this test is equivalent to a two-tailed t-test.
, i.e. this test is equivalent to a two-tailed t-test.
Here we can determine an exact distribution for LR, or rather the equivalent test statistics  , i.e.
, i.e.

However, in general, the distribution of LR (under  ) is difficult to determine and we need to use the approximate
) is difficult to determine and we need to use the approximate  method.
method.
Fisher's method of scoring
Multiparameter case
Let  be i.i.d. with
be i.i.d. with

with p.d.f.

that is  .
.
Log-likelihood:
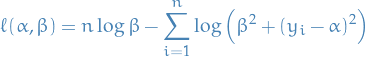
Score vector:
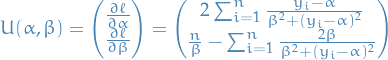
Hessian matrix:
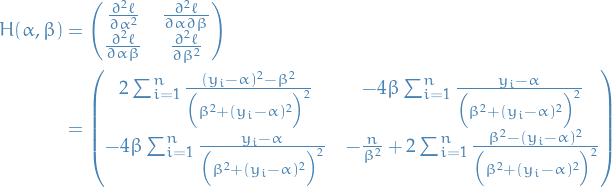
Observed information matrix:
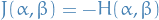
Expected information matrix:
![\begin{equation*}
I(\alpha, \beta) = - \mathbb{E}[H(\alpha, \beta)] = \frac{n}{2 \beta^2} \begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}
\end{equation*}](../../assets/latex/probability_and_statistics_a7a6320450411e834e2766e9352c5b500bc8579b.png)
Asymptotic variance-covariance matrix of
 is:
is:
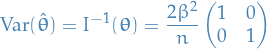
Estimated standard errors:

Covariance between our estimates:
Asymptotic distribution:
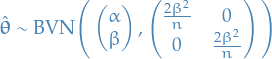
Which is the distribution we would base a Wald test of
 on, i.e.
on, i.e.
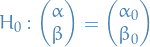
Asymptotics
Overview
- A lot of it based on van2000asymptotic
Notation
For a measure
 on a measurable space
on a measurable space  and a measurable function
and a measurable function  ,
,
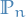 denotes the empirical measure, such that
denotes the empirical measure, such that
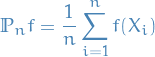
 denotes the empirical process, i.e. the "cenetered & scaled" version of
denotes the empirical process, i.e. the "cenetered & scaled" version of  ,
,
![\begin{equation*}
\mathbb{G}_n f = \sqrt{n} \big( \mathbb{P}_n f - Pf \big) = \frac{1}{\sqrt{n}} \sum_{i=1}^{n} \big( f(X_i) - \mathbb{E}_p [ f(X_i) ] \big)
\end{equation*}](../../assets/latex/probability_and_statistics_0a81db4efc68ca9ee36cce132512331704d0f806.png)
 denotes a P-Brownian bridge
denotes a P-Brownian bridge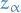 denotes the upper α-quantie of a std. normal
denotes the upper α-quantie of a std. normal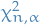 denotes the upper α-quantie of a χ²-distribution
denotes the upper α-quantie of a χ²-distribution denotes the upper α-quantie of a t-distribution
denotes the upper α-quantie of a t-distribution denotes absolutely continuous
denotes absolutely continuous denotes contiguous
denotes contiguous denotes mutually contiguous
denotes mutually contiguous denotes weak convergence, and if
denotes weak convergence, and if  has distribution
has distribution  , we also write
, we also write 
For a given sequence of random variables

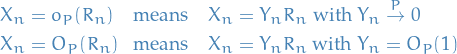
where
 denotes the fact that a sequence is bounded in probability.
denotes the fact that a sequence is bounded in probability.
Stochastic convergence
For any random vectors  and
and  the following statements are equivalent
the following statements are equivalent
 for all continuity points of
for all continuity points of 
![$\mathbb{E} [f(X_n)] \to \mathbb{E}[f(X)]$](../../assets/latex/probability_and_statistics_e3aad164dab5cf25ef60f779a7acf1b5f440b7fa.png) for all bounded, continuous functions
for all bounded, continuous functions  , i.e.
, i.e. 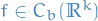
![$\mathbb{E} [f(X_n)] \to \mathbb{E}[f(X)]$](../../assets/latex/probability_and_statistics_e3aad164dab5cf25ef60f779a7acf1b5f440b7fa.png) for all bounded, Lipschitz functions
for all bounded, Lipschitz functions 
![$\liminf \mathbb{E}[f(X_n)] \ge \mathbb{E}[f(X)]$](../../assets/latex/probability_and_statistics_3eb0d92d6baec89d54582e97d1e0437e702ad17d.png) for all nonnegative, continuous functions
for all nonnegative, continuous functions 
 for every open set
for every open set 
 for every closed set
for every closed set 
 for all Borel sets
for all Borel sets  with
with  , where
, where  is the boundary of
is the boundary of 
lemma:portmanteau-weak-convergence-equivalences is a very useful lemma for talking about convergences in
Any random vector  is tight : for every
is tight : for every 

A set of random vectors 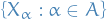 is called uniformly tight if
is called uniformly tight if 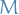 can be chosen the same for every
can be chosen the same for every 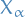 : for every
: for every 

Thus, there exists a compact set to which all 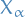 give probability "almost" one.
give probability "almost" one.
Another name of uniformly tight is bounded in probability.
Let  be random vectors in
be random vectors in  .
.
- If
 for some
for some  , then
, then  is uniformly tight.
is uniformly tight. - If
 is uniformly tight, then there exists a subsequence with
is uniformly tight, then there exists a subsequence with  as
as  for some
for some  .
.
Prohorov's theorem states that every uniformly tight sequence contains a weakly converging subsequence. This basically generalizes the Heine-Borel theorem to random vectors.
Characteristic functions
Let  and
and  be random vectors in
be random vectors in  . Then
. Then
![\begin{equation*}
X_n \leadsto X \quad \iff \quad \mathbb{E} \big[ e^{i t^T x_n} \big] \to \mathbb{E} \big[ e^{i t^T X} \big], \quad \forall t \in \mathbb{R}^k
\end{equation*}](../../assets/latex/probability_and_statistics_676407f91683756d1605ffde81c570712b706c97.png)
Moreover, if ![$\mathbb{E} \big[ e^{it^T X_n} \big]$](../../assets/latex/probability_and_statistics_09f0e4437758136600aa4be8668f990335e5a939.png) convergences pointwise to a function
convergences pointwise to a function  that is continuous at zero, then
that is continuous at zero, then  is the characteristic function of a random vector
is the characteristic function of a random vector  and
and  .
.
Statistical Learning Theory
Notation
Binary classification
Notation
 denotes the training data for the algorithm
denotes the training data for the algorithm and
and 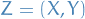 for convenience
for convenience denotes the class of binary classifiers considered, and thus
denotes the class of binary classifiers considered, and thus
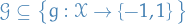
Symmetrization
- Idea: replace the true risk
 by an estimate computed on an independent set of data, i.e.
by an estimate computed on an independent set of data, i.e.  (called a virtual or ghost sample)
(called a virtual or ghost sample)
For any  .s.t that
.s.t that  ,
,
![\begin{equation*}
\Pr \bigg[ \sup_{f \in \mathcal{F}} \big( P - P_n \big)f \ge t \bigg] \le 2 \Pr \bigg[ \sup_{f \in \mathcal{F}} \big( P_n' - P_n \big)f \ge t / 2 \bigg]
\end{equation*}](../../assets/latex/probability_and_statistics_2e47076fbc441cd4ab0390a9cc753c4f38bcc02b.png)
where
 denotes the empirical measure of the "ghost" sample
denotes the empirical measure of the "ghost" sample 
Stuff
For a class  of functions, the Rademacher average is defined as
of functions, the Rademacher average is defined as
![\begin{equation*}
\mathcal{R}(\mathcal{F}) = \mathbb{E} \Big[ \sup_{f \in \mathcal{F}} R_n f \Big]
\end{equation*}](../../assets/latex/probability_and_statistics_606bb8834f77d4808279fe9419d8f22420fb0d4a.png)
where
 is defined
is defined
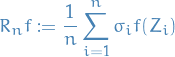
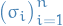 are Rademacher random variables, i.e. i.i.d. such that
are Rademacher random variables, i.e. i.i.d. such that  .
. denotes the expectation over all the rvs, i.e.
denotes the expectation over all the rvs, i.e. 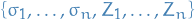
Similarily, the conditional Rademacher average is defined as
![\begin{equation*}
\mathcal{R}_n(\mathcal{F}) := \mathbb{E}_{\sigma} \Big[ \sup_{f \in \mathcal{F}} R_n f \Big]
\end{equation*}](../../assets/latex/probability_and_statistics_abbe3201f982b43430093f75f0b1b6414ea61623.png)
where
 denotes the expectation only over the rvs
denotes the expectation only over the rvs  , conditioned on
, conditioned on 
For all  , with probability at least
, with probability at least 
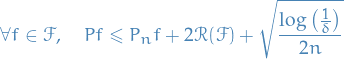
and also, with prob. at least  ,
,
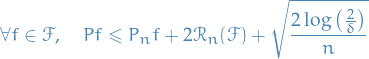
where
True risk
![\begin{equation*}
Pf := \mathbb{E} \big[ f(X, Y) \big]
\end{equation*}](../../assets/latex/probability_and_statistics_bd938671795fdb30032bec6ae59f9a6b0d25a59d.png)
Empirical risk
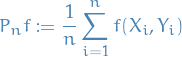
Topics in Statistical Theory
1.2 Estimating an arbitrary distribution function
Let
 denote the class of all dsitribution functions on
denote the class of all dsitribution functions on 

Empirical distribution
 is given by
is given by
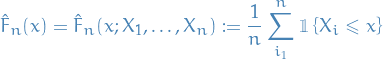
We have
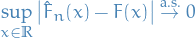
as  .
.
Given  , let
, let  .
.
Set 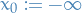 , and
, and

and  .
.
Writing  , which we can do since
, which we can do since  is left-continuous, we note that
is left-continuous, we note that

Let
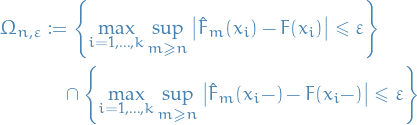
where
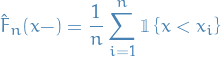
(note the that this has uses strict inequality). Hence, by a union bound, we have
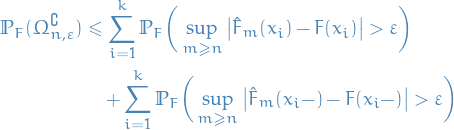
which, by SLLN the terms in the absolute values goes to zero a.s. as  , therefore implying that
, therefore implying that

Now fix  and find
and find  s.t.
s.t.  . Then for any
. Then for any  and
and  ,
,
where in the second inequality we use the fact that  .
.
Similarily, for the other way around, we have
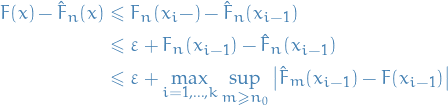
From the two equations above, it follows that
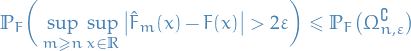
since either we have
 : in which case the event on the LHS can occur if
: in which case the event on the LHS can occur if

 : in which case the event on the LHS can occur if
: in which case the event on the LHS can occur if
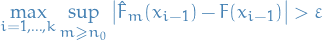 1
1
Hence the probability of such an event is upper-bounded by the RHS  .
.
We therefore conclude that
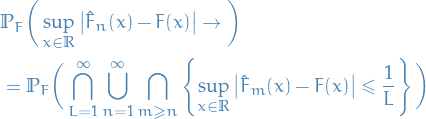
i.e. for all  ,
,  such that
such that  , the difference is less than
, the difference is less than  .
.
In particular, note that the probability on the RHS is:
- Decreasing in
 (since the event becomes smaller as
(since the event becomes smaller as  increases)
increases) - Increasing in
 (since the "number of"
(since the "number of"  we're taking the intersection for decreases)
we're taking the intersection for decreases)
This means that we have
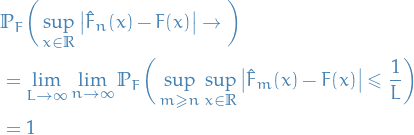
as we wanted.
1.3
Let
 be a sequence of random vectors in
be a sequence of random vectors in 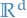
Suppose  and a random vector
and a random vector  such that
such that

as  .
.
Furthermore, suppose that 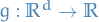 is differentabile at
is differentabile at  .
.
Then

This can be seen by using expanding using the Taylor expansion at  .
.
1.4. Concentraion Inequalities
We say the random variable  is sub-Gaussian with parameter
is sub-Gaussian with parameter 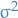 if
if ![$\mathbb{E}[X] = 0$](../../assets/latex/probability_and_statistics_56be98dff9b0eedfc7b4bba0860fc3638ddd82e1.png) and it has MGF
and it has MGF
![\begin{equation*}
\mathbb{E} \big[ e^{tX} \big] \le e^{t^2 \sigma^2 / 2}, \quad \forall t \in \mathbb{R}
\end{equation*}](../../assets/latex/probability_and_statistics_3c5fed34a5a24bc4a09dd636e33331db17ddf3af.png)
For any  , we have
, we have

By Markov's inequality we have
![\begin{equation*}
\begin{split}
\mathbb{P} \big( X \ge x \big) &\le \frac{\mathbb{E} \big[ e^{tX} \big]}{e^{t x}} \\
&\le e^{- tx} e^{t^2 \sigma^2 / 2}
\end{split}
\end{equation*}](../../assets/latex/probability_and_statistics_afba67577dddf6d382535edd3322ebf9ac549984.png)
where in the second inequality we used the fact that  is sub-Gaussian with parameter
is sub-Gaussian with parameter 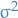 . Since this holds for any
. Since this holds for any  ,
,

The RHS attains the minimum at 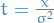 (this can be seen by expanding the square and the solving the resulting quadratic), thus
(this can be seen by expanding the square and the solving the resulting quadratic), thus
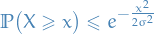
as claimed!
Let  be independent r.v.s. with
be independent r.v.s. with
![$\mathbb{E} [X_i] = 0$](../../assets/latex/probability_and_statistics_0be76112efe56b9d813f5c9b0b78863d116153ec.png)
- finite variances
 for some
for some 
Moreover, let

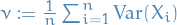
 defined by
defined by
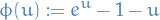
Then, for every  ,
,
![\begin{equation*}
\log \mathbb{E} \big[ e^{t S} \big] \le \frac{n \nu}{b^2} \phi(b t)
\end{equation*}](../../assets/latex/probability_and_statistics_c5369980d547464e6c9ea0a741d8e6d7bc0bc90e.png)
Consequently, defining
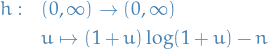
we have that for  ,
,

Define
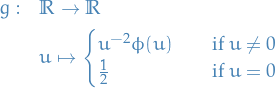
where the definition at 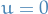 , is simply to ensure continuity for all
, is simply to ensure continuity for all  .
.
Then 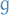 is icnreasing, so for
is icnreasing, so for  ,
,
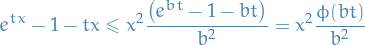
Hence, for  ,
,
![\begin{equation*}
\begin{split}
\log \mathbb{E} \big[ e^{t S} \big] &= \sum_{i = 1}^{n} \log \mathbb{E} \big[ e^{t X_i} \big] \\
&\le \sum_{i = 1}^{n} \log \bigg( 1 + \mathbb{E}\big[ X_i^2 \big] \frac{\phi(bt)}{b^2} \bigg) \\
&\le n \log \bigg( 1 + \frac{\nu \phi(bt)}{b^2} \bigg) \\
&\le n \frac{\nu \phi(bt)}{b^2}
\end{split}
\end{equation*}](../../assets/latex/probability_and_statistics_3fd7d9524ee3bb240d57fee17a0e2c1b38e5780c.png)
where in the
- second to last inequality we have multiplied by
 and used Jensen's inequality,
and used Jensen's inequality, - final inequality we used the fact that
 for
for  .
.
Consequently, by a Chernouff bound,
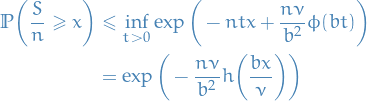
since the infimum is attained at  .
.
Bibliography
Bibliography
- [arjovsky17_wasser_gan] Arjovsky, Chintala, Bottou & L\'eon, Wasserstein Gan, CoRR, (2017). link.
- [roberts04_gener_state_space_markov_chain_mcmc_algor] Roberts & Rosenthal, General State Space Markov Chains and Mcmc Algorithms, CoRR, (2004). link.
- [gelman2013bayesian] Gelman, Carlin, Stern, Dunson, Vehtari & Rubin, Bayesian data analysis, Chapman and Hall/CRC (2013).
- [adrian13_count_model_based_weibul_inter_times] Adrian, Bradlow, Fader, & McShane, Count Models Based on Weibull Interarrival Times, CoRR, (2013). link.
- [yannaros1994weibull] Yannaros, Weibull renewal processes, Annals of the Institute of Statistical Mathematics, 46(4), 641-648 (1994).
- [clauset07_power_law_distr_empir_data] Clauset, Shalizi, & Newman, Power-Law Distributions in Empirical Data, CoRR, (2007). link.
- [so_you_think_you_have_a_power_law_shalizi] Cosma Shalizi, So You Think You Have a Power Law - Well Isn't That Special?, link.. (Accessed on 05/22/2018)
- [likelihood_ratio_test_for_model_selection_and_non_nested_hypothesis_vyong89] Quang Vuong, Likelihood Ratio Tests for Model Selection and Non-Nested Hypotheses, Econometrica, 57(2), 307-333 (1989). link.
- [van2000asymptotic] Van der Vaart, Asymptotic statistics, Cambridge university press (2000).

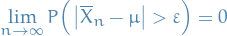





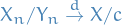



 is
is  , and
, and
![\begin{equation*}
\mathbb{E}[X_{\tau}] = X_0
\end{equation*}](../../assets/latex/probability_and_statistics_cc5d570588453c1c6a2ae039f13292fbb9eaf912.png)
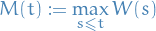

 .
.
![\begin{equation*}
\hat{\alpha} = 1 + n \Bigg[ \sum_{i=1}^{n} \ln \bigg( \frac{x_i}{x_{\text{min}}} \bigg) \Bigg]
\end{equation*}](../../assets/latex/probability_and_statistics_d8a4d2a65ef8ba890eae5d9d647be1ca78498eb1.png)

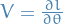
![\begin{equation*}
W_{\psi} [f] (a, b) = \left\langle f, \psi_{a, b} \right\rangle = \int_{-\infty}^{\infty} f(t) \bar{\psi}_{a, b} (t) \ dt
\end{equation*}](../../assets/latex/probability_and_statistics_072b1d09828023553b81c052fc4af8c8fb5d6b66.png)

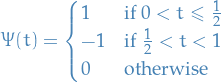

 is the
is the 
