Linear Algebra
Table of Contents
Definitions
Ill-conditoned matrix
A matrix  is ill-conditioned if small changes in its entries can produce large
changes in the olutisns to
is ill-conditioned if small changes in its entries can produce large
changes in the olutisns to  . If small changes in the entries
of
. If small changes in the entries
of  produce small changes in the solutions to
produce small changes in the solutions to  , then
, then  is called well-conditioned.
is called well-conditioned.
Singular values
For any  matrix
matrix  , the
, the 
 is symmetric and thus orthogonally diagonalizable
by the Spectral Theorem.
is symmetric and thus orthogonally diagonalizable
by the Spectral Theorem.
The eigenvalues of  are real and non-negative. Therefore,
are real and non-negative. Therefore,
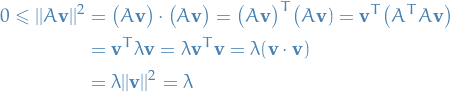 1
1
where  is a unit eigenvector of
is a unit eigenvector of  . Hence, we can take the square root
of all these eigenvalues, and define what we call singular values:
. Hence, we can take the square root
of all these eigenvalues, and define what we call singular values:
If  is an
is an  matrx, the singular values of
matrx, the singular values of  are the square roots
of the eigenvalues of
are the square roots
of the eigenvalues of  and are denoted
and are denoted  .
.

By convention we order the singular values s.t.  .
.
Cholesky decomposition
The Cholesky decomposition or Cholesky factorization is a decomposition of a Hermitian positive-definite matrix into a product of lower triangular matrix and it's conjugate transpose:

where  is lower-triangular.
is lower-triangular.
Every Hermitian matrix  has a unique Cholesky decomposition.
has a unique Cholesky decomposition.
A real Cholesky factor is unique up to sign of the columns.
Suppose  is Cholesky factor of some matrix. The matrix components are then given by
is Cholesky factor of some matrix. The matrix components are then given by

So by scaling the k-th column by -1 we get
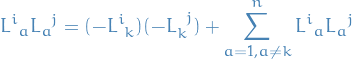
So it ain't no matter:)
Sidenote: summing all the way to  is redundant because all indices larger than
is redundant because all indices larger than  vanishes.
vanishes.
Theorems
Spectral Theorem
Let  be an
be an  real matrix. Then
real matrix. Then  is symmetric iff it is orthogonally diagonalizable.
is symmetric iff it is orthogonally diagonalizable.
Singular Value Decomposition
Let  be an
be an  matrix with singular values
matrix with singular values  and
and
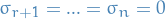 . Then there exists:
. Then there exists:
 orthogonal matrix
orthogonal matrix 
 orthogonal matrix
orthogonal matrix 
 "diagonal" matrix
"diagonal" matrix  , where
, where 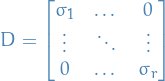
such that:

See page 615 of "Linear Algebra: A Modern Introduction" :)
Constructing V
To construct the orthogonal matrix  , we first find an orthonormal basis
, we first find an orthonormal basis  for
for  consisting of eigenvectors of the
consisting of eigenvectors of the  symmetric matrix
symmetric matrix  . Then
. Then
![\begin{equation*}
V = [ \mathbf{v}_1 \cdots \mathbf{v}_n ]
\end{equation*}](../../assets/latex/linear_algebra_379644cea68ba33c9ab9c11aa9187e8fa8d7bab8.png)
is an orthogonal matrix.
Constructing U
For the orthogonal matrix  , we first note that
, we first note that  is an orthogonal set of vectors
in
is an orthogonal set of vectors
in  (we're NOT saying they form a basis in
(we're NOT saying they form a basis in  !). To see this, suppose that
!). To see this, suppose that  is a
eigenvector of
is a
eigenvector of  corresponding to the eigenvalue
corresponding to the eigenvalue  . Then, for
. Then, for  , we have
, we have
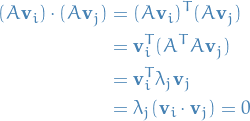
since the eigenvectors are orthogonal.
Since  we can normalize
we can normalize  by
by
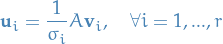
This guarantees that  is a orthonormal set in
is a orthonormal set in  ,
but if
,
but if  it's not a basis. In this case, we extend
it's not a basis. In this case, we extend  to an orthonormal basis
to an orthonormal basis  for
for  by some
technique, e.g. the Gram-Schmidt Process, giving us
by some
technique, e.g. the Gram-Schmidt Process, giving us
![\begin{equation*}
U = [ \mathbf{u}_1 \cdots \mathbf{u}_m ]
\end{equation*}](../../assets/latex/linear_algebra_8bd4e5a916a48fdd78852a680c82aaeb5f042556.png)
Outer Product Form of the SVD
Let  be an
be an  matrix with singular values
matrix with singular values  and
and 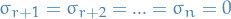 , then
, then

Geometric insight into the effect of matrix transformations
Let  be an
be an  matrix with rank
matrix with rank  . Then the image of the unit sphere in
. Then the image of the unit sphere in  under the matrix transformation that maps
under the matrix transformation that maps  to
to 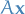 is
is
- the surface of a an ellipsoid in
 if
if 
- a solid ellipsoid in
 if
if 
We have  with
with  . Then
. Then
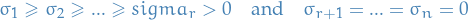
Let  (i.e. unit vector = surface of unit sphere) in
(i.e. unit vector = surface of unit sphere) in 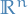 .
.
 is orthogonal, thus
is orthogonal, thus  is orthogonal and then
is orthogonal and then  is a unit vector too.
is a unit vector too.
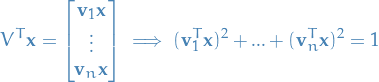
From the Outer Product Form we have:
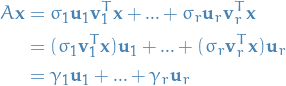
where we are letting 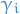 denote the scalar
denote the scalar  .
.
(1) If 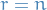 , then we must have
, then we must have  and
and
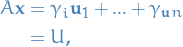
Since  is orthogonal, we have
is orthogonal, we have  , thus
, thus
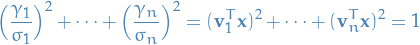
which shows that the vectors 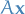 form the surface of an ellipsoid in
form the surface of an ellipsoid in  !
!
(2) If  , swapping equality with inequality (but performing the same steps):
, swapping equality with inequality (but performing the same steps):
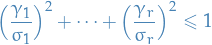
where the inequality corresponds to a solid ellipsoid in  !
!
Furthermore, we can view the each of the matrix transformations of the SVD separately:
 is an orthogonal matrix, thus it maps the unit sphere onto itself (but in a different basis)
is an orthogonal matrix, thus it maps the unit sphere onto itself (but in a different basis) matrix
matrix  first collapses to
first collapses to  dimensions of the unit sphere,
leaving a unit sphere of
dimensions of the unit sphere,
leaving a unit sphere of  dimensions, and then "distorts" into an ellipsoid
dimensions, and then "distorts" into an ellipsoid is orthogonal, aligning the axes of this ellipsoid with the orthonormal basis vectors $ 1, …, r$ in
is orthogonal, aligning the axes of this ellipsoid with the orthonormal basis vectors $ 1, …, r$ in 
Least squares solution for dependent column-vectors
The least squares problem  has a unique least squares solution
has a unique least squares solution  of minimal
length that is given by:
of minimal
length that is given by:

See page 627 of "Linear Algebra: A Modern Introduction" :)
Determinant
Trace is the sum of the eigenvalues
Let  be a matrix, then
be a matrix, then
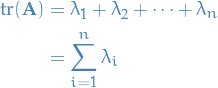
We start with the characteristic equation
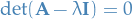
We then notice that

which can be seen by expanding the determinant along the diagonal:
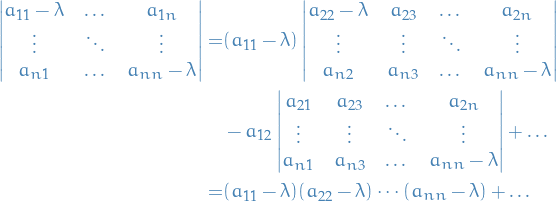
Here we see that the only "sub-determinant" which contains a factor of  is going to be the very first one which is multiplied by
is going to be the very first one which is multiplied by  , since each of the other "sub-determinants" will not have a coefficient with
, since each of the other "sub-determinants" will not have a coefficient with  , and it will not contain
, and it will not contain  , hence at most contain a factor of
, hence at most contain a factor of  .
.
Further, since
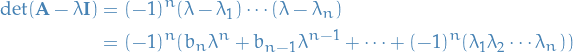
we observe that 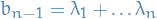 , which we also know to be the
, which we also know to be the  from above, i.e.
from above, i.e.
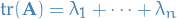
as wanted.
Determinant is the product of the eigenvalues
Let  be a matrix, then
be a matrix, then
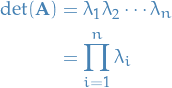
Let  be a matrix. Then
be a matrix. Then
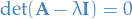
defines the characteristic equation, which as the eigenvalues  as its roots, therefore
as its roots, therefore
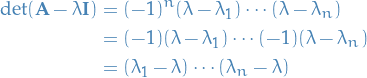
Since  is just a variable, we let
is just a variable, we let  and get
and get
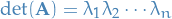
as wanted.
Cramers Rule
Consider the system of  linear equations represented by
linear equations represented by  unknowns; in matrix form
unknowns; in matrix form

where  has nonzero determinant, then
has nonzero determinant, then
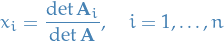
where  is the matrix formed by replacing the i-th column of
is the matrix formed by replacing the i-th column of  by the column vector
by the column vector  .
.
The reason why we can think of OLS as projection
The proof of the following theorem is really important in my opinion, as it provides a "intuitive" way of viewing least-squares approximations.
The Best Approximation Theorem says the following:
If 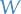 is a finite-dimensional subspace of an inner product space
is a finite-dimensional subspace of an inner product space  and if
and if  is a vector in
is a vector in  , then
, then  is the best approximation to
is the best approximation to  in
in 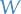 .
.
Let  be a vector in
be a vector in 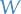 different from
different from  .
Then
.
Then  is also in
is also in 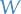 , so
, so  is orthogonal to
is orthogonal to  .
.
Pythagoras' Theorem now implies that
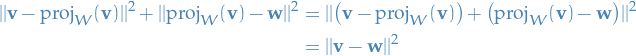
But  , so
, so

i.e.  and thus that
and thus that  is the best approximation.
is the best approximation.
Distance and Approximation
Applications
Function-approximation
Given a continunous function  on an interval
on an interval ![$[a, b]$](../../assets/latex/linear_algebra_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) and a subspace
and a subspace 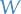 of
of ![$\mathcal{C}[a, b]$](../../assets/latex/linear_algebra_522cb05ba5d1c97eeff01816075d0fba81fe6149.png) ,
find the function "closest" to
,
find the function "closest" to  in
in 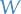 .
.
![$\mathcal{C}[a, b]$](../../assets/latex/linear_algebra_522cb05ba5d1c97eeff01816075d0fba81fe6149.png) denotes the space of all continuous functions defined on the domain
denotes the space of all continuous functions defined on the domain ![$[a, b]$](../../assets/latex/linear_algebra_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png)
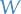 is a subspace of
is a subspace of ![$\mathcal{C}[a, b]$](../../assets/latex/linear_algebra_522cb05ba5d1c97eeff01816075d0fba81fe6149.png)
Problem is analogous to least squares fitting of data points, except we have infinitely
many data points - namely, the points in the graph of the function  .
.
What should "approximate" mean in this context? Best Approximation Theorem has the answer!
The given function  lives in the vector space
lives in the vector space ![$\mathcal{C}[a, b]$](../../assets/latex/linear_algebra_522cb05ba5d1c97eeff01816075d0fba81fe6149.png) of continuous functions on
the interval
of continuous functions on
the interval ![$[a, b]$](../../assets/latex/linear_algebra_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) . This is an inner product space, with inner product:
. This is an inner product space, with inner product:
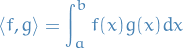
If 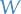 is finite-dimensional subspace of
is finite-dimensional subspace of ![$\mathcal{C}[a, b]$](../../assets/latex/linear_algebra_522cb05ba5d1c97eeff01816075d0fba81fe6149.png) , then the best approximation to
, then the best approximation to
 in
in 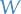 is given by the projection of
is given by the projection of  onto
onto 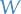 .
.
Furthermore, if  is an orthogonal basis for
is an orthogonal basis for 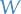 , then
, then
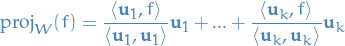
The error from this approximation is just
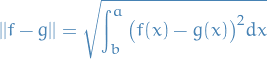
and is often called the root mean square error. For functions we can think of this as the area between the graphs.
Fourier approximation
A function of the form

is called a trigonometric polynomial.
Restricting our attention to the space of continuous functions
on the interval ![$[- \pi, \pi ]$](../../assets/latex/linear_algebra_dab0d85594f921c74674fee47916c345db89fbca.png) , i.e.
, i.e. ![$\mathcal{C}[-\pi, \pi]$](../../assets/latex/linear_algebra_40ef2fba60d64669dd52c0be6c03a02d90ecf040.png) , with the inner product
, with the inner product
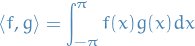
and since the trigonometric polynomials are linear combinations of the set

the best approximation to a function  in
in ![$\mathcal{C}[-\pi, \pi]$](../../assets/latex/linear_algebra_40ef2fba60d64669dd52c0be6c03a02d90ecf040.png) by
trigonometric polynomials of order
by
trigonometric polynomials of order  is therefore
is therefore  ,
where
,
where 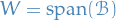 . It turns out that
. It turns out that  is an orthogonal set,
hence a basis for
is an orthogonal set,
hence a basis for 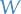 .
.
The approximation to  using trigonometric polynomials is called the
n-th order Fourier approximation to
using trigonometric polynomials is called the
n-th order Fourier approximation to  on
on ![$[-\pi, \pi]$](../../assets/latex/linear_algebra_aa62fe947306d8dbe0a258bbfdc3c84c03ffff2f.png) , with the coefficients
are known as Fourier coefficients of
, with the coefficients
are known as Fourier coefficients of  .
.
Rayleigh principle
A lot of the stuff here I got from these lecture notes.
Notation
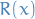 denotes the Rayleigh coefficient of some Herimitian / real symmetric matrix
denotes the Rayleigh coefficient of some Herimitian / real symmetric matrix 
 is the diagonal matrix with entries being eigenvalues of
is the diagonal matrix with entries being eigenvalues of 
- Eigenvalues are ordered as

 is the orthogonal matrix with eigenvectors of
is the orthogonal matrix with eigenvectors of  as columns
as columns , thus
, thus 
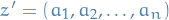
Definition
For a given complex Hermitian matrix  and non-zero vector
and non-zero vector  , the Rayleigh quotient is defined as:
, the Rayleigh quotient is defined as:
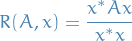
In the case of  ,
,  and is symmetric, then
and is symmetric, then
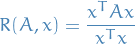
Further, in general,
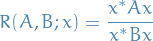
is the generalized Rayleigh quotient, where  is a positive-definite Herimitian matrix.
is a positive-definite Herimitian matrix.
The generalized Rayleigh quotient can be reduced to 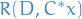 through the transformation
through the transformation

where  is the Cholesky decomposition of the Hermitian positive-definite matrix
is the Cholesky decomposition of the Hermitian positive-definite matrix  .
.
Minimization
Personal explanation
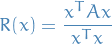
At the maximum we must have

But observe that for whatever  we have here, we have
we have here, we have

i.e. it's invariant to scaling.
Further, since  is symmetric, we have the diagonalization
is symmetric, we have the diagonalization

which means that if we let

for some  , we get
, we get

where we've applied the constraint  , which we can since again, invariant under scaling.
, which we can since again, invariant under scaling.
Therefore, we're left with the following optimization problem:
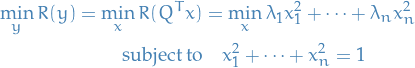
Since we assume that  , we clearly obtain the minima when
, we clearly obtain the minima when
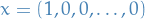
Hence,

where  denotes the corresponding eigenvector.
denotes the corresponding eigenvector.
Now suppose we'd like to find the minima, which is NOT in the space spanned by the first eigenvector, then we only consider the subspace

Thus, the optimization problem is
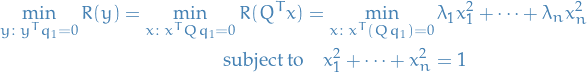
Finally, observe that 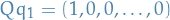 , hence
, hence
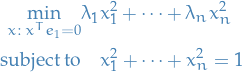
And the subspace 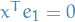 is just all
is just all 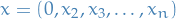 , giving us
, giving us
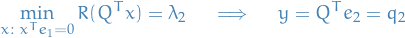
And if we just keep going, heyooo, we get all our eigenvalues and eigenvectors!
Stuff
We're going to assume  is real.
is real.
Our objective is:

Observe the following:
- Objective is invariant to scaling, since we'd be scaling the denominator too
 is by assumption symmetric: all real eigenvalues
is by assumption symmetric: all real eigenvalues
Thus, we have

Further,

Hence,
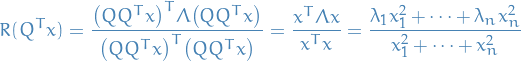
Thus, by letting  , we get
, we get
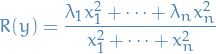
Since this quotient is invariant under scaling, we frame it as follows:
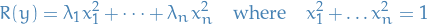
Implying that ![$R(y) \in [\lambda_1, \lambda_n]$](../../assets/latex/linear_algebra_8dcc526f9d7daac89b97f0e234be47ae85de1bf8.png) (seen from
(seen from 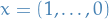 and
and 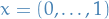 ) since we assume the eigenvalues to be ordered.
) since we assume the eigenvalues to be ordered.
Hence, we have proved what's called the Rayleigh Principle:

where  is the smallest eigenvalue of
is the smallest eigenvalue of  .
.
Planar Slices
Suppose we'd like to find the answer to the following:

i.e. minimizing the Rayleigh quotient over some hyperplane defined by  .
.
This minimum is bounded blow as follows:

Further, we can obtain an upper bound for this by considering  again:
again:
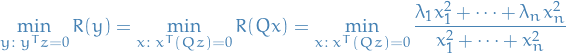
By scaling we can assume  , giving us the optimization problem
, giving us the optimization problem
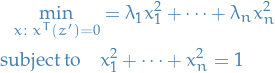
There is at least one vector of the form

If  , then the above translates to
, then the above translates to
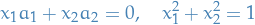
assuming  (does not satisfy second constraint), then the first constraint can be represented as:
(does not satisfy second constraint), then the first constraint can be represented as:
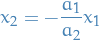
which is just a line through the origin. The second constraint is the unit-circle. Thus, there are only two points where both these constraints are satisfied (a line crosses the circle in two places). Let 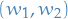 be one of these points of intersection, then
be one of these points of intersection, then

Which means we have bounded the minimum of 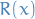 on the hyperplane
on the hyperplane  ! This becomes incredibly useful when have a look at Minimax Principle for the Second Smallest Eigenvalue.
! This becomes incredibly useful when have a look at Minimax Principle for the Second Smallest Eigenvalue.
Minimax Principle for the Second Smallest Eigenvalue
This is a slighly different way of viewing finding the second eigenvalue, and poses the "answer" in a frame where we might have asked the following question:
"Can we obtain 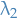 without finding
without finding  ?"
?"
And ends with the answer:

which is very useful computationally, as we can alternate between miniziming and maximizing 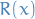 to obtain
to obtain 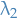 .
.
What if we could attain the maximum in this equation such that we would know that "maximizing in the hyperplane  , where
, where  minimizes
minimizes 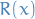 , gives us the second smallest eigenvalue
, gives us the second smallest eigenvalue 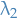 !
!
Or equivalently, the minimum in the restricted hyperplane  is given by
is given by 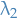 !
!
Thus, if we can force somehow force  and
and  , then we would get a upper bound for this. If we had
, then we would get a upper bound for this. If we had 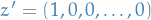 then the only solutions to this would be:
then the only solutions to this would be:

To show that  , we only consider solutions for
, we only consider solutions for  where
where 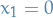 , i.e. let
, i.e. let
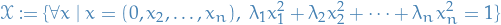
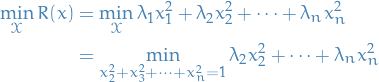
Which is clearly attained when 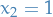 and
and 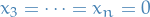 , since
, since 
Hence,

Thus we've shown that min-maxing over some function 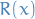 is equivalent of finding the second smallest eigenvalue!
is equivalent of finding the second smallest eigenvalue!
Since  means that
means that  lies in the orthogonal complement of
lies in the orthogonal complement of  , which is an (n-1)-dimensional subspace. Thus, we may rewrite the above as
, which is an (n-1)-dimensional subspace. Thus, we may rewrite the above as

In fact, it turns out this works for general  :
:

All this means that if we want to find some vector  which minimizes the Rayleigh quotient, then we simply compute the eigenvalues of
which minimizes the Rayleigh quotient, then we simply compute the eigenvalues of  and look for the corresponding eigenvector, giving us the solution!
and look for the corresponding eigenvector, giving us the solution!