Calculus

Table of Contents

Calculus

Definitions

Norm / mesh of partition

The norm ( or mesh ) of the partition

\begin{equation*} x_0 < x_1 < x_2 < \dots < x_n \end{equation*}

is the length of the longest of these subintervals:

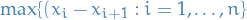
\begin{equation*} \max \{ (x_i - x_{i + 1} : i = 1, \dots, n \} \end{equation*}

Riemann-Stieltjes integral

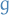The Riemann-Stieltjes integral of a real-valued function $f$ of a real variable with respect to a real function $g$ is denoted by

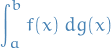
\begin{equation*} \int_a^b f(x) \ dg(x) \end{equation*}

and defined to be the limit, as the norm of the partition

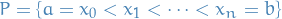
\begin{equation*} P = \{ a = x_0 < x_1 < \dots < x_n = b \} \end{equation*}

of the interval $[a, b]$ approaches zero, of the approximating sum

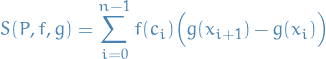
\begin{equation*} S(P, f, g) = \sum_{i=0}^{n-1} f(c_i) \Big( g(x_{i+1}) - g(x_i) \Big) \end{equation*}

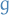where $c_i$ is in the i-th subinterval $[x_i, x_{i + 1}]$. The two functions $f$ and $g$ are respectively called the integrand and the integrator.

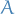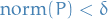The "limit" is understood to be a number $A$ (value of the Riemann-Stieltjes integral) such that for every $\varepsilon > 0$ there exists a $\delta > 0$ s.t. every partition $P$ with $\text{norm}(P) < \delta$, and for every choice of points $c_i$ in $[x_i, x_{i + 1}]$,

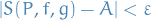
\begin{equation*} |S(P, f, g) - A| < \varepsilon \end{equation*}
Comparison to Riemann integral

The Riemann integral for the case used in the definition above we have

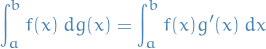
\begin{equation*} \int_a^b f(x) \ dg(x) = \int_a^b f(x) g'(x) \ dx \end{equation*}

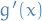Now, what's the difference between this and the Riemann-Stieltjes integral? The main point is that the Riemann-Stieltjes integral allow us to integrate wrt. the function $g(x)$ itself rather than to $g'(x)$ and then wrt. $x$. In this way it extends the Riemann integral and is slightly more "general".

Equations / Theorems

Fundamental Theorem of Calculus

Jensen's Inequality

Let 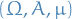$(\Omega, A, \mu)$ be a probability space, i.e. 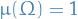$\mu(\Omega) = 1$, where

Then if

  • $g$ is real-valued function that is $\mu$ -integrable
  • $\varphi$ is a convex function on the real line

we have:

\begin{equation*} \varphi \Big( \int_\Omega g \ d \mu \Big) \le \Big( \int_\Omega \varphi \circ g \ d \mu \Big) \end{equation*}
TODO Proof

Vector calculus

Definitions

Conservative vector field

A conservative vector field is a vector field that is the gradient of some function, know in this context as a scalar potential.

Conservative vector fields have the property that a line integral is path independent , i.e. the choice of any path between two points does not change the value of the line integral.

Equations / Theorems

(Gauss') Divergence Theorem

"Integral definition"

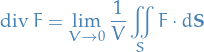
\begin{equation*} \text{div } F = \lim_{V \rightarrow 0} \frac{1}{V} \iint_S F \cdot d \mathbf{S} \end{equation*}

From what I can tell, this looks like the "approximation" near some point which can be arrived at from the Divergence Theorem using Stokes' Theorem. See this section for what I'm talking about.

Multivariate Taylor Expansion

\begin{equation*} f(\mathbf{x}) = f(\mathbf{a}) + \Big[(\mathbf{x} - \mathbf{a}) \cdot \Big( \boldsymbol{\nabla} \cdot f(\mathbf{x}) \Big) \Big] + \Big[ (\mathbf{x} - \mathbf{a}) \cdot \Big( H(\mathbf{x}) \cdot (\mathbf{x} - \mathbf{a}) \Big) \Big] + ... \end{equation*}

Vector field identities

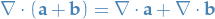
\begin{equation*} \nabla \cdot ( \mathbf{a} + \mathbf{b} ) = \nabla \cdot \mathbf{a} + \nabla \cdot \mathbf{b} \end{equation*}
\begin{equation*} \nabla \times (\mathbf{a} + \mathbf{b}) = \nabla \times \mathbf{a} + \nabla \times \mathbf{b} \end{equation*}
\begin{equation*} \nabla \cdot (\phi \mathbf{a}) = (\nabla \phi) \cdot \mathbf{a} + \phi (\nabla \cdot \mathbf{a}) \end{equation*}
\begin{equation*} \nabla \times ( \phi \mathbf{a} ) = ( \nabla \phi) \times \mathbf{a} + \phi (\nabla \times \mathbf{a}) \end{equation*}
\begin{equation*} \nabla \cdot (\mathbf{a} \times \mathbf{b} ) = \mathbf{b} \codt (\nabla \times \mathbf{a} ) - \mathbf{a} \cdot (\nabla \times \mathbf{b}) \end{equation*}
\begin{equation*} \nabla \times (\mathbf{a} \times \mathbf{b}) = (\nabla \cdot \mathbf{b}) \mathbf{a} + (\mathbf{b} \cdot \nabla ) \mathbf{a} - (\nabla \cdot \mathbf{a}) \mathbf{b} - (\mathbf{a} \cdot \nabla) \mathbf{b} \end{equation*}
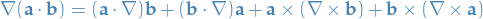
\begin{equation*} \nabla (\mathbf{a} \cdot \mathbf{b}) = (\mathbf{a} \cdot \nabla) \mathbf{b} + (\mathbf{b} \cdot \nabla) \mathbf{a} + \mathbf{a} \times (\nabla \times \mathbf{b}) + \mathbf{b} \times (\nabla \times \mathbf{a}) \end{equation*}
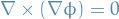
\begin{equation*} \nabla \times (\nabla \phi) = 0 \end{equation*}
\begin{equation*} \nabla \cdot (\nabla \times \mathbf{a}) = 0 \end{equation*}
\begin{equation*} \nabla \times (\nabla \times \mathbf{a}) = \nabla (\nabla \cdot \mathbf{a}) - \nabla^2 \mathbf{a} \end{equation*}

Elementary identities

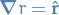
\begin{equation*} \boldsymbol{\nabla} r = \hat{\mathbf{r}} \end{equation*}
\begin{equation*} \boldsymbol{\nabla} r^n = n r^{n-2} \mathbf{r} \end{equation*}
\begin{equation*} \boldsymbol{\nabla} \times \mathbf{r} = 0 \end{equation*}
\begin{equation*} \boldsymbol{\nabla} (\mathbf{a} \cdot \mathbf{r}) = \mathbf{a} \end{equation*}
\begin{equation*} (\mathbf{a} \cdot \boldsymbol{\nabla} ) \mathbf{r} = \mathbf{a} \end{equation*}
\begin{equation*} \boldsymbol{\nabla} \times (\mathbf{a} \times \mathbf{r}) = 2 \mathbf{a} \end{equation*}
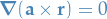
\begin{equation*} \boldsymbol{\nabla}(\mathbf{a} \times \mathbf{r}) = 0 \end{equation*}

Essential Calculus: Early Transcendentals

11 Vector Calculus

11.6 Directional Derivatives and the Gradient Vector

Directional Derivative

Finding the derivative of some function $f$ at some point $\mathbf{x}_0$ in the direction of some arbitrary unit vector $\mathbf{u}$.

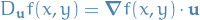\begin{equation*} D_{\mathbf{u}} f(x, y) = \boldsymbol{\nabla} f(x, y) \cdot \mathbf{u} \end{equation*} 1

Which expresses the directional derivative in the direction of $\mathbf{u}$ as the scalar projection of the gradient vector onto $\mathbf{u}$.

  • Maximizing the Directional Derivative

    Suppose $f$ is a differentiable function of two or three variables. The maximum value of the directional derivative $D_{\mathbf{u}} f( \mathbf{x})$ is $|\nabla f(\mathbf{x})|$ and it occurs when $\mathbf{u}$ has the same direction as the gradient vector $\nabla f(\mathbf{x})$.

    \begin{equation*} D_{\mathbf{u}} f = \nabla f \cdot \mathbf{u} = | \nabla f| \ |\mathbf{u}| \cos \theta = | \nabla f | \cos \theta \end{equation*}

    Which is simply maximized when $\theta = 0$, i.e. $\mathbf{u}$ has the same direction as $\nabla f$.

    This just says that $f$ has it's maximum change in the direction of $\nabla f$. If you're at some point $P$, and what the direction to move for maximum change in $f$, move in the direction of $\nabla f$.

Tangent Planes to Level Surfaces

Let:

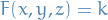  • $S$ is a surface with equation $F(x, y, z) = k$, i.e. it is a level surface of a function $F$
  • $P(x_0, y_0, z_0)$ be a point on $S$
  • $C$ be any curve that lies on the surface $S$ and pass through the point $P$, i.e. $\mathbf{r}(t) = \langle x(t), y(t), z(t) \rangle$ where $t_0 \ | \ \mathbf{r}(t_0) = \langle x_0, y_0, z_0 \rangle$

Then any point $(x(t), y(t), z(t))$ must satisfy the equation of $S$, that is:

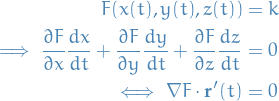
\begin{equation*} \begin{split} F(x(t), y(t), z(t)) &= k \\ \implies \frac{\partial F}{\partial x} \frac{dx}{dt} + \frac{\partial F}{\partial y} \frac{dy}{dt} + \frac{\partial F}{\partial z} \frac{dz}{dt} &= 0 \\ \iff \nabla F \cdot \mathbf{r}'(t) &= 0 \end{split} \end{equation*}

Which says that the gradient vector $\nabla F$ of $F$ is orthogonal to the gradient of any curve $C$ lying on $S$ that passes through $P$. Furthermore, this defines the a plane with the normal vector $\nabla F$ and so we have a rather general definition of a tangent plane.

This makes sense intuitively, because as we move away from the point $P$ while staying on the level surface $S$, the value of $F$ does not change. That's the entire point of a level surface: $S = \{ (x, y, z) : F(x, y, z) = k \}$ for some $k$. And the direction of maximum increase is then orthogonal to the level surface $S$.

Notice where this comes in? Gradient descent. If we instead move the opposite of the gradient, i.e. orthogonal to the level surface $S$ but in the "negative" direction, we got ourselves the entire premise of GD.

11.8 Lagrange Multipliers

Overview

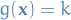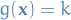Goal is to find extreme values of $f(\mathbf{x})$ subject to the constraint $g(\mathbf{x}) = k$. In other words, we seek the extreme values of $f(\mathbf{x})$ when the point $\mathbf{x}$ is restriced to lie on the level curve $g(\mathbf{x}) = k$.

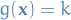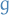To maximize $f(\mathbf{x})$ wrt. $g(\mathbf{x})$ is then to find the largest value $c$ such that the level curve $f(\mathbf{x}) = c$ intersects $g(\mathbf{x}) = k$. This happens when $f$ and $g$ have the same tangent line . Otherwise, the value of $c$ could be increased further. This means that the normal lines at the point $\mathbf{x}_0$ are parallel !

\begin{equation*} \nabla f(\mathbf{x}) = \lambda \nabla g(\mathbf{x}), \quad \lambda \in \mathbb{R} \end{equation*}
Algorithm

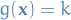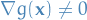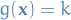To find the maximum and minimum values of $f(\mathbf{x})$ subject to the constraint $g(\mathbf{x}) = k$ [assuming that these extreme values exist and $\nabla g(\mathbf{x}) \ne 0$ on the surface $g(\mathbf{x}) = k$]:

a) Find all values of $\mathbf{x}$ and $\lambda$, s.t.:

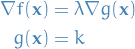
\begin{equation*} \begin{split} \nabla f(\mathbf{x}) &= \lambda \nabla g(\mathbf{x}) \\ g(\mathbf{x}) &= k \end{split} \end{equation*}

b) Evaluate $f$ at all points $\mathbf{x}$ that result from step (a). The largest of these values is the maximum value of $f$: the smallest is the minimum value of $f$.

13 Vector Calculus

Notation

  • $C$ denotes a curve
  • $\mathbf{r}(t)$ defines the path of the curve $C$
  • $D$ denotes the region enclosed by the curve $C$
  • positive orientation of a simple closed curve $C$ refers to a single counterclockwise traversal of $C$, i.e. the region $D$ is always on the left as the point $\mathbf{r}(t)$ traverses $C$

13.4 Green's Theorem

This theorem gives us a neat "trick" to compute integrals for certain types of closed surfaces.

Let $C$ be a positively oriented, piecewise-smooth, single closed curve in the plane and let $D$ be the region bounded by $C$. If $P$ and $Q$ have continuous partial derivatives on an open region that contains $D$, then

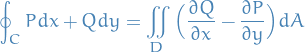
\begin{equation*} \oint_C P dx + Q dy = \iint_D \Big( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \Big) dA \end{equation*}

Notice that we have a proof if we can show that

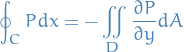
\begin{equation*} \oint_C P dx = - \iint_D \frac{\partial P}{\partial y} dA \end{equation*}

and

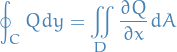
\begin{equation*} \oint_C Q dy = \iint_D \frac{\partial Q}{\partial x} dA \end{equation*}

We write the region $D$ as:

\begin{equation*} D = \big\{ (x, y) | a \le x \le b, g_1(x) \le y \le g_2(x) \big\} \end{equation*}

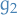where $g_1$ and $g_2$ are continuous functions.

Then,

\begin{equation*} \iint_D \frac{\partial P}{\partial y} \ dA = \int_a^b \int_{g_1(x)}^{g_2(x)} \frac{\partial P}{\partial y}(x, y) \ dy\ dx = \int_a^b [P(x, g_2(x)) - P(x, g_1(x))] \ dx \end{equation*}

where the last step follows from the Fundamental Theorem of Calculus.

If the entire curve is smooth, we got our result. If it's only piecewise smooth, we then treat the curve $C$ as a union of piecewise smooth curves, and compute the integral for each of these piecewise curves making up $C$.

Note that when computing this for the piecewise case, we need to make sure that we choose the correct sign for each of the integrals, i.e. sign s.t. that positive means enclosed surface is on the left.

Green's Theorem can also be extended to include surfaces with holes , i.e. regions which are NOT simply-connected .

This is done by splitting regions in such a way that we instead end up with multiple simply-connected surfaces.

See p. 787 in the book.

Vector forms

The following expresses Green's Theorem as the line integral of the tangential component of $\mathbf{F}$ along $C$ as the double integral of the vertical component of $\text{curl} \ \mathbf{F}$ over the region D enclosed by $C$ .

\begin{equation*} \oint_C \mathbf{F} \cdot \ d \mathbf{r} = \iint_D (\text{curl} \ \mathbf{F}) \cdot \mathbf{k} \ dA \end{equation*}

The other following expresses Green's Theorem as the line integral of the normal component of $\mathbf{F}$ along $C$ is equal to the double integral of the divergence of $\mathbf{F}$ over the region $D$ enclosed by $C$ .

\begin{equation*} \oint_C \mathbf{F} \cdot \mathbf{n} ds = \iint_D \text{div} \ \mathbf{F}(x, y) \ dA \end{equation*}

13.5 Curl and Divergence

Curl

If $\mathbf{F} = P \mathbf{i} + Q \mathbf{j} + R \mathbf{k}$ is a vector field on $\mathbb{R}^3$ and the partial derivatives of $P$, $Q$, and $R$ all exist, then the curl of $\mathbf{F}$ is the vector field on $\mathbb{R}^3$ defined by

\begin{equation*} \text{curl} \ \mathbf{F} = \nabla \times \mathbf{F} \end{equation*}
  • Why the name "curl"?
    • Curl vecto is associated with rotations
    • Another occus when $\mathbf{F}$ represents the velocity field in fluid flow. Particles near $(x, y, z)$ in the fluid tend to rotate about the axis that points in the direction of $\text{curl} \ \mathbf{F}(x, y, z)$ and the length of this curl vector is a measure of how quickly the particles move around the axis.
Divergence

If $\mathbf{F} = P \mathbf{i} + Q \mathbf{j} + R \mathbf{k}$ is a vector field on $\mathbb{R}^3$ and $P$, $Q$, and $R$ have continuous second-order partial derivatives, then

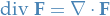
\begin{equation*} \text{div} \ \mathbf{F} = \nabla \cdot \mathbf{F} \end{equation*}
  • Why the name "divergence"?

    Again, in the context of fluid flow .

    If 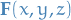$\mathbf{F}(x, y, z)$ is the velocity field of a fluid, then $\text{div} \ \mathbf{F}(x, y, z)$ represents the net rate of change (wrt. time) of the mass of the fluid flowing from point $(x, y, z)$ per unit volume.

    In other words, $\text{div} \ \mathbf{F}$ measures the tendency of the fluid to diverge from the point $(x, y, z)$.

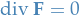    If $\text{div} \ \mathbf{F} = 0$, then $\mathbf{F}$ is said to be incompressible.

13.7 Surface Integrals

If $\mathbf{F}$ is a continuous vector field defined on an oriented surface $S$ with a unit normal vector $\mathbf{n}$, then the surface integral of $\mathbf{F}$ over $S$ is

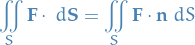
\begin{equation*} \iint_S \mathbf{F} \cdot \ d \mathbf{S} = \iint_S \mathbf{F} \cdot \mathbf{n} \ dS \end{equation*}

This integral is also called the flux of $\mathbf{F}$ across $S$.

And since:

\begin{equation*} \mathbf{n} = \frac{\mathbf{r}_u \times \mathbf{r}_v}{|| \mathbf{r}_u \times \mathbf{r}_v ||} \end{equation*}

we can also a surface integral:

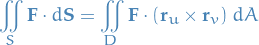
\begin{equation*} \iint_S \mathbf{F} \cdot d \mathbf{S} = \iint_D \mathbf{F} \cdot (\mathbf{r}_u \times \mathbf{r}_v) \ dA \end{equation*}
Applications in Physics
  • Notation
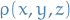    • $\rho(x, y, z)$ fluid density at $(x, y, z)$
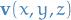    • $\mathbf{v}(x, y, z)$ velocity field
    • $S$ is surface the fluid is flowing through
  • Fluid flow

    We can approximate the mass of fluid crossing a segment of the surface, $S_{ij}$, in the direction of the normal $\mathbf{n}$ per unit time by the quantity:

    \begin{equation*} (\rho \mathbf{v} \cdot \mathbf{n}) A(S_{ij}) \end{equation*}

    where $A(S_{ij})$ is the area of the surface-segment $S_{ij}$.

    Then by definition of a surface integral, summing these elements and taking the limit we get the rate of flow through the surface $S$ as:

    \begin{equation*} \Phi(\mathbf{v}) = \iint_s \rho \mathbf{v} \cdot \mathbf{n} \ dS \end{equation*}

    Also known as the flux.

Stoke's Theorem

Let $S$ be an oriented piecewise-smooth surface that is bounded by a simple, closed, piecewise-smooth boundary curve $C$ with positive orientation. Let $\mathbf{F}$ be a vector field whose components have continuous partial derivatives on an open region in $\mathbb{R}^3$ that contains $S$. Then

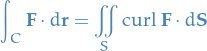
\begin{equation*} \int_C \mathbf{F} \cdot d \mathbf{r} = \iint_S \text{curl} \ \mathbf{F} \cdot d \mathbf{S} \end{equation*}

The book says I'm not smart enough to know yet. Some day…

Green's Theorem is a special case of Stoke's Theorem.

Shedding light on the curl of a vector field

Using Stoke's Theorem we can shed some more light on $\text{curl} \ \mathbf{F}$.

Suppose that $C$ is an oriented closed curve and $\mathbf{v}$ represents the velocity field in fluid flow. Consider the line integral

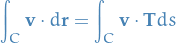
\begin{equation*} \int_C \mathbf{v} \cdot d \mathbf{r} = \int_C \mathbf{v} \cdot \mathbf{T} ds \end{equation*}

and recall that $\mathbf{v} \cdot \mathbf{T}$ is the component of $\mathbf{v}$ in the direction of the unit tangent vector $\mathbf{T}$.

This means that the closer the direction of $\mathbf{v}$ is to the direction of $\mathbf{T}$, the larger the value of $\mathbf{v} \cdot \mathbf{T}$. Thus $\int_C \mathbf{v} \cdot d \mathbf{r}$ is a measure of the tendency of the fluid to move around $C$ and is called the circulation of $\mathbf{v}$ around $C$.

Now let $P_0(x_0, y_0, z_0)$ be a point in the fluid and let $S_a$ be a small disk with radius $a$ and center $P_0$. Then $(\text{curl} \ \mathbf{F})(P) \approx (\text{curl} \ \mathbf{F})(P_0)$ for all points $P$ on $S_a$ becuase $\text{curl} \ \mathbf{F}$ is continuous.

Thus, by Stokes' Theorem, we get the following approximation to the circulation around the boundary circle $C_a$:

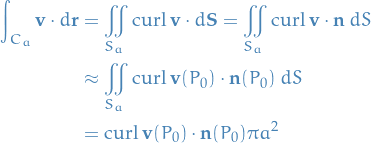
\begin{equation*} \begin{split} \int_{C_a} \mathbf{v} \cdot d \mathbf{r} &= \iint_{S_a} \text{curl} \ \mathbf{v} \cdot d \mathbf{S} = \iint_{S_a} \text{curl} \ \mathbf{v} \cdot \mathbf{n} \ dS \\ & \approx \iint_{S_a} \text{curl} \ \mathbf{v}(P_0) \cdot \mathbf{n}(P_0) \ dS \\ &= \text{curl} \ \mathbf{v}(P_0) \cdot \mathbf{n}(P_0) \pi a^2 \end{split} \end{equation*}

This approximation becomes better as $a \rightarrow 0$ and we have

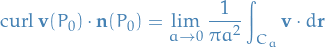
\begin{equation*} \text{curl} \ \mathbf{v}(P_0) \cdot \mathbf{n}(P_0) = \lim_{a \rightarrow 0} \frac{1}{\pi a^2} \int_{C_a} \mathbf{v} \cdot d \mathbf{r} \end{equation*}

Hence, we have a relationship between the curl and the circulation, where we can view the 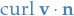$\text{curl} \ \mathbf{v} \cdot \mathbf{n}$ as a measure of the rotating effect of the fluid about the axis $\mathbf{n}$.

The curling effect is greatest about the axis parallel to $\text{curl} \ \mathbf{v}$.

13.9 The Divergence Theorem

Let $E$ be a simple solid region and let $S$ be the boundary surface of $E$, given with positive (outward) orientation. Let $\mathbf{F}$ be a vector field whose component functions have continuous partial derivatives on an open region that contains $E$. Then

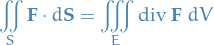
\begin{equation*} \iint_S \mathbf{F} \cdot d \mathbf{S} = \iiint_E \text{div} \ \mathbf{F} \ dV \end{equation*}

Thus the Divergence Theorem states that, under the given conditions, the flux of $\mathbf{F}$ across the boundary surface of $E$ is equal to the triple integral of the divergence of $\mathbf{F}$ over $E$.