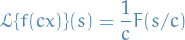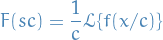Differential Equations
Table of Contents
Stuff
Spectral method
A class of techniques to numerical solve certain differential equations. The idea is to write a solution of the differential equation as a sum of certain "basis functions" (e.g. Fourier Series which is a sum of sinouids) and then choose the coefficients in the sum in order to satisfy the differential equation as well as possible.
Series solutions
Definitions
Suppose we have a second-order differential equation of the form

where  ,
,  and
and  are polynomials.
are polynomials.
We then rewrite the equation as

Then we say the point  is
is
- an ordinary point if the functions
 and
and  are analytic at
are analytic at 
- singular point if the functions aren't analytic
Convergence
Have a look at p. 248 in "Elementary Differential Equations and Boundary Problems". The two pages that follow summarizes a lot of different methods which can be used to determine convergence of a power series.
Systems of ODEs
Overview
The main idea here is to transform some n-th order ODE into a system of  1st order ODEs, which we can the solve using "normal" linear algebra!
1st order ODEs, which we can the solve using "normal" linear algebra!
Procedure
Consider an arbitrary n-th order ODE

- Change dependent variables to
 :
:

- Take derivatives of the new variables
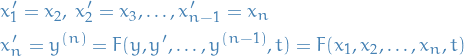
Homogenous
Fundamental matrices
Suppose that  form a fundamental set of solutions for the equation
form a fundamental set of solutions for the equation
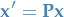
on some interval  . Then the matrix
. Then the matrix
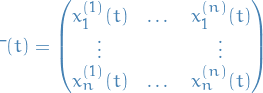
whose columns are the vectors  , is said to be a fundamental matrix for the system.
, is said to be a fundamental matrix for the system.
Note that the fundamental matrix is nonsingular / invertible since the solutions are lin. indep.
We reserve the notation  for the fundament matrices of the form
for the fundament matrices of the form
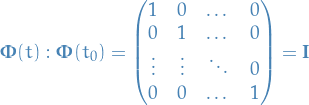
i.e. it's just a fundamental matrix parametrised in such a way that our initial conditions gives us the identity matrix.
The solution of an IVP of the form:

can then be written

which can also be written

Finally, we note that

The exponential of a matrix is given by
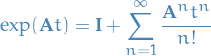
and we note that it satisfies differential equations of the form
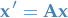
since
![\begin{equation*}
\frac{d}{dt} [ \exp(\mathbf{A} t) ] = \sum_{n=1}^{\infty} \frac{\mathbf{A}^n t^{n-1}}{(n - 1)!} = \mathbf{A} \Bigg[ \mathbf{I} + \sum_{n=1}^{\infty} \frac{\mathbf{A}^n t^n}{n!} \Bigg] = \mathbf{A} \exp(\mathbf{A} t)
\end{equation*}](../../assets/latex/differential_equations_06d795474fca16fce328d45f50a633c5620b8197.png)
Hence, we can write the solution of the above differential equation as

Repeating eigenvalues
Suppose we have a repeating eigenvalue 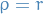 (of algebraic multiplicity 2), with the found solution correspondig to
(of algebraic multiplicity 2), with the found solution correspondig to  is
is
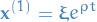
where  satisfies
satisfies
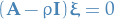
We then assume the other solution to be of the form

where  is determined by the equation
is determined by the equation

Multiplying both sides by  we get
we get

since  by definition. Solving the above equation for
by definition. Solving the above equation for  and substituting that solution into the expression for
and substituting that solution into the expression for 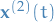 we get the second solution corresponding to the repeated eigenvalue.
we get the second solution corresponding to the repeated eigenvalue.
We call the vector  the generalized eigenvector of
the generalized eigenvector of  .
.
Non-homogenous
We want to solve the ODE systems of the form

Which has a general solution of the form
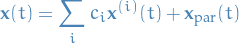
where  is the general solution to the corresponding homogenous ODE system.
is the general solution to the corresponding homogenous ODE system.
We discuss the three methods of solving this:
Diagonolisation
We assume the corresponding homogenous system is solved with the eigenvalues  and eigenvectors
and eigenvectors  , and then introduce the change of variables
, and then introduce the change of variables 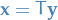 :
:
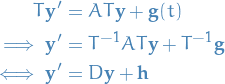
which gives us a system of  decoupled systems:
decoupled systems:
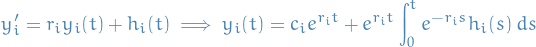
and finally we transform back to the original variables:

- Example
Consider
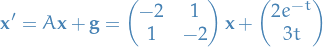
Since the system is linear and non-homogeneous, the general solution must be of the form

where
 denotes the particular solution.
denotes the particular solution.
The homogenous solution can be found as follows:
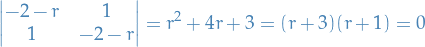
When
 : if
: if  , hence we choose
, hence we choose

When
 : if
: if 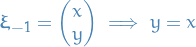 , hence we choose
, hence we choose
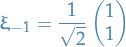
Thus, the general homogenous solution is:

To find the particular solution, we make the change of variables
 :
:

With the new variables the ODE looks as follows:
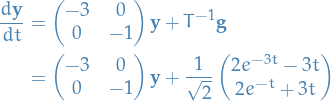
Which in terms of
 is
is
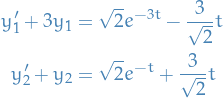
Which, by the use of undetermined coefficients, we can solve as
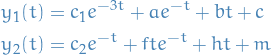
Doing "some" algebra, we eventually get
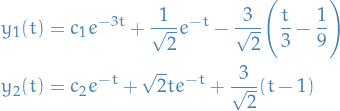
Then, finally, substituting back into the equation for
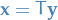 , and we would get the final result.
, and we would get the final result.
Undetermined coefficients
This method only works if the coefficient matrix  for some constant matrix
for some constant matrix  , and the components of
, and the components of  are polynomial, exponential, or sinusoidal functions, or sums or products of these.
are polynomial, exponential, or sinusoidal functions, or sums or products of these.
Variation of parameters
This is the most general way of doing this.
Suppose we have the n-th order linear differential equation
![\begin{equation*}
L[y] = y^{(n)} + p_1(t) y^{(n - 1)} + \dots + p_{n - 1}(t) y' + p_n(t)y = g(t)
\end{equation*}](../../assets/latex/differential_equations_7b69465c5ec334852dc1292a5f0c7f52ff8f68ae.png)
Suppose we have found the solutions to the corresponding homogenous diff. eqn.

With the method of variation of parameters we seek a particular solution of the form

Since we have  functions
functions  to determine we have to specify
to determine we have to specify  conditions.
conditions.
One of these conditions is cleary that we need to satisfy the non-homongenous diff. eqn. above. Then the 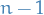 other conditions are chosen to make the computations as simple as possible.
other conditions are chosen to make the computations as simple as possible.
Taking the first partial derivative wrt.  of
of  we get (using the product rule)
we get (using the product rule)

We can hardly expect it to be simpler to determine  if we have to solve diff. eqns. of higher order than what we started out with; hence we try to surpress the terms that lead to higher derivatives of
if we have to solve diff. eqns. of higher order than what we started out with; hence we try to surpress the terms that lead to higher derivatives of  by imposing the following condition
by imposing the following condition

which we can do since we're just looking for some arbitrary functions  . The expression for
. The expression for  then reduces to
then reduces to

Continuing this process for the derivatives  we obtain our
we obtain our 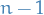 condtions:
condtions:
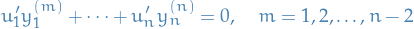
giving us the expression for the m-th derivative of  to be
to be

Finally, imposing that 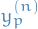 has to satisfy the original non-homogenous diff. eqn. we take the derivative of
has to satisfy the original non-homogenous diff. eqn. we take the derivative of  and substitute back into the equation. Doing this, and grouping terms involving each of
and substitute back into the equation. Doing this, and grouping terms involving each of  together with their derivatives, most of the terms drop out due to
together with their derivatives, most of the terms drop out due to  being a solution to the homogenous diff. eqn., yielding
being a solution to the homogenous diff. eqn., yielding

Together with the previous 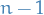 conditons we end up with a system of linear equations
conditons we end up with a system of linear equations
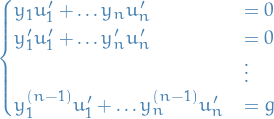
(note the 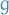 at the end!).
at the end!).
The sufficient condition for the existence of a solution of the system of equations is that the determinant of coefficients is nonzero for each value of  . However, this is guaranteed since
. However, this is guaranteed since  form a fundamental set of solutions for the homogenous eqn.
form a fundamental set of solutions for the homogenous eqn.
In fact, using Cramers rule we can write the solution of the system of equations in the form

where  is the determinant of obtained from
is the determinant of obtained from 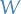 by replacing the m-th column by
by replacing the m-th column by  . This gives us the particular solution
. This gives us the particular solution
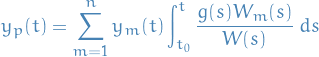
where  is arbitrary.
is arbitrary.
Assume that a fundamental matrix  for the corresponding homogenous system
for the corresponding homogenous system
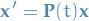
has been found. We can then use the method of variation of parameters to construct a particular solution, and hence the general solution, of the non-homogenous system.
The general solution to the homogenous system is  , we seek a solution to the non-homogenous system by replacing the constant vector
, we seek a solution to the non-homogenous system by replacing the constant vector  by a vector function
by a vector function  . Thus we assume that
. Thus we assume that

is a solution, where  is a vector function to be found.
is a vector function to be found.
Upon differentiating  we get
we get

Since  is a fundamental matrix,
is a fundamental matrix,  ; hence the above expression reduces to
; hence the above expression reduces to

Since  is nonsingular (i.e. invertible) on any interval where
is nonsingular (i.e. invertible) on any interval where  is continuous. Hence
is continuous. Hence 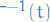 exists, and therefore
exists, and therefore

Thus for  we can select any vector from the class of vectors which satisfy the previous equation. These vectors are determined only up to an arbitrary additive constant vector; therefore, we denote
we can select any vector from the class of vectors which satisfy the previous equation. These vectors are determined only up to an arbitrary additive constant vector; therefore, we denote  by
by
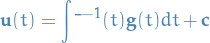
where the constant vector  is arbitrary.
is arbitrary.
Finally, this gives us the general solution for a non-homogenous system
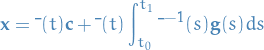
Dynamical systems
In 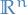 , an arbitrary autonomous dynamical system can be written as
, an arbitrary autonomous dynamical system can be written as
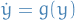
for some smooth  , for a the 2D case:
, for a the 2D case:

which in matrix notation we write
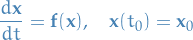
Notation
 denotes a critical point
denotes a critical point denotes the RHS of the autonomous system
denotes the RHS of the autonomous system denotes a specific solution
denotes a specific solution
Theorems
The critical point  of the linear system
of the linear system
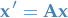
where we suppose  has eigenvalues
has eigenvalues 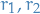 , is:
, is:
- asymptotically stable if
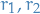 are real and negative
are real and negative - stable if
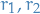 are pure imaginary
are pure imaginary - unstable if
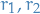 are real and either positive, or have positive real part
are real and either positive, or have positive real part
Stability
The points  are called critical points of the autonomous system
are called critical points of the autonomous system

Let  be a critical point of the system.
be a critical point of the system.
 is said to be stable if for any
is said to be stable if for any  ,
,
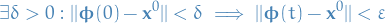
for all
 .
I.e. for some solution
.
I.e. for some solution  we parametrize it such that
we parametrize it such that  for some
for some  such that we stay close to
such that we stay close to  for all
for all  , then we say it's stable.
, then we say it's stable.
 is said to be asymptotically stable if it's stable and there exists a
is said to be asymptotically stable if it's stable and there exists a  s.t. that if a solution
s.t. that if a solution  satisfies
satisfies

then

i.e. if we start near
 , the limiting behaviour converges to
, the limiting behaviour converges to  . Note that this is stronger than just being stable.
. Note that this is stronger than just being stable.
 which is NOT stable, is of course unstable.
which is NOT stable, is of course unstable.
Intuitively what we're saying here is that:
- for any
 we can find a trajectory (i.e. solution with a specific initial condition, thus we can find some initial condition ) such that the entire trajectory stays within
we can find a trajectory (i.e. solution with a specific initial condition, thus we can find some initial condition ) such that the entire trajectory stays within  of the critical points for all
of the critical points for all  .
.
When we say a critical point is isolated, we mean that there are no other critical points "nearby".
In the case of a system

By solving the equation

if the solution  is a single vector, rather than a line or plane, the critical point
is a single vector, rather than a line or plane, the critical point  is not isolated.
is not isolated.
Suppose that we have the system

and that  is a isolated critical point of the system. We also assume that
is a isolated critical point of the system. We also assume that  so that
so that  is also a isolated critical point of the linear system
is also a isolated critical point of the linear system 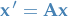 . If
. If

that is, 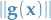 is small in comparison to
is small in comparison to  near the critical point
near the critical point  , we say the system is a locally linear system in the neighborhood of the critical point
, we say the system is a locally linear system in the neighborhood of the critical point  .
.
Linearized system
In the case where we have a locally linear system, we can approximate the system near isolated critical points by instead considering the Jacobian of the system. That is, if we have the dynamical system

with a critical point at  , we can use the linear approximation of
, we can use the linear approximation of  near
near  :
:

where  denotes the Jacobian of
denotes the Jacobian of  , which is
, which is
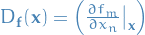
Substituting back into the ODE

Letting  , we can rewrite this as
, we can rewrite this as

which, since  is constant given
is constant given  , gives us a linear ODE wrt
, gives us a linear ODE wrt  , hence the name linearization of the dynamical system.
, hence the name linearization of the dynamical system.
Hopefully  is a simpler expression than what we started out with.
is a simpler expression than what we started out with.
General procedure
- Obtain critical points, i.e.
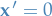
- If non-linear and locally linear, compute the Jacobian and use this is an linear approximation to the non-linear system, otherwise: do nothing.
- Inspect the following to determine the behavior of the system:
 and
and 
- Compute eigenvalues and eigenvectors to obtain solution of the (locally) linear system
- Consider asymptotic behavior of the different terms in the general solution, i.e.

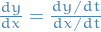 which provides insight into the phase diagram / surface. If non-linear, first do for linear approx., then for non-linear system
which provides insight into the phase diagram / surface. If non-linear, first do for linear approx., then for non-linear system
Points of interest
The following section is a very short summary of Ch. 9.1 [Boyce, 2013]. Look here for a deeper look into what's going on, AND some nice pictures!
Here we consider 2D systems of 1st order linear homogenous equations with constant coefficients:
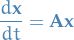
where  and
and  . Suppose
. Suppose 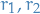 are the eigenvalues for the matrix
are the eigenvalues for the matrix  , and thus gives us the expontentials for the solution
, and thus gives us the expontentials for the solution  .
.
We have multiple different cases which we can analyse:
 :
:
- Exponential decay: node or nodal sink
- Exponential growth. node or nodal source
 : saddle point
: saddle point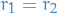 :
:
- two independent eigenvectors: proper node (sometimes a star point )
- one independent eigenvector: improper or degenerate node
 : spiral point
: spiral point
- spiral sink refers to decaying spiral point
- spiral source refers to growing spiral point
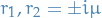 : center
: center
Basin of attraction
This denotes the set of all points  in the xy-plane s.t. the trajectory passing through
in the xy-plane s.t. the trajectory passing through  approaches the critical point as
approaches the critical point as  .
.
A trajectory that bounds the basin of attraction is called a separatix.
Limit cycle
Limit cycles are periodic solutions such that at least one other non-closed trajectory asymptotes to them as  and / or
and / or  .
.
Let  and
and 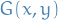 have continuous first partial derivatives in a simply connected domain
have continuous first partial derivatives in a simply connected domain  .
.
If  has the same sign in the entire
has the same sign in the entire  , then there are no closed trajectories in
, then there are no closed trajectories in  .
.
Consider the system

Let  and
and 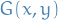 have continious first partial derivatives in a domain
have continious first partial derivatives in a domain  .
.
Let  be a bounded subdomain of
be a bounded subdomain of  and let
and let  .
Suppose
.
Suppose  contains no critical points.
contains no critical points.
If

then
- solution is periodic (closed trajectory)
- OR it spirals towards a closed trajectory
Hence, there exists a closed trajectory.
Where
 denotes a particular trajectory
denotes a particular trajectory denotes the boundary of
denotes the boundary of 
Useful stuff
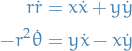
- Example
Say we have the following system:
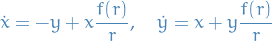
where
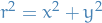 , has periodic solutions corresponding to the zeroes of
, has periodic solutions corresponding to the zeroes of  .
What is the direction of the motion on the closed trajectories in the phase plane?
.
What is the direction of the motion on the closed trajectories in the phase plane?
Using the identities above, we can rewrite the system as
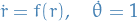
Which tells us that the trajectories are moving in counter-clockwise direction.
Lyapunov's Second Method
Goal is to obtain information about the stability or instability of the system without explicitly obtaining the solutions of the system. This method allows us to do exactly that through the construction of a suitable auxillary function, called the Lyapunov function.
For the 2D-case, we consider such a function of the following form:

where  and
and 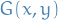 are as given in the autonomous system definition.
are as given in the autonomous system definition.
We choose the notation above because  can be identified as the rate of change of
can be identified as the rate of change of  along the trajectory of the system that passes through the point
along the trajectory of the system that passes through the point  . That is, if
. That is, if 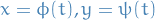 is a solution of the system, then
is a solution of the system, then
![\begin{equation*}
\begin{split}
\frac{d V[\phi(t), \psi(t)]}{d t} &= V_x [\phi(t), \psi(t)] \frac{d \phi(t)}{dt} + V_y [\phi(t), \psi(t)] \frac{d \psi(t)}{dt} \\
&= V_x(x, y) F(x, y) + V_y(x, y) G(x, y) \\
&= \dot{V}(x, y)
\end{split}
\end{equation*}](../../assets/latex/differential_equations_eb6d5d1753dd4ece351488567e383c226b6440d5.png)
Suppose that the autonomous system has an isolated critical point at the origin.
If there exists a continuous and positive definite function  which also has continuous first partial derivatives
which also has continuous first partial derivatives  :
:
- if
 ( negative definite ) on some domain
( negative definite ) on some domain  , then the origin is an asymptotically stable critical point
, then the origin is an asymptotically stable critical point - if
 ( negative semidefinite ) then the origin is a stable point
( negative semidefinite ) then the origin is a stable point
Suppose that the autonomous system has an isolated critical point at the origin.
Let  be a function that is continuous and has continuous first partial derivatives.
be a function that is continuous and has continuous first partial derivatives.
Suppose that  and that in every neighborhood of the origin there is a least one point at which
and that in every neighborhood of the origin there is a least one point at which  is positive (negative). If there exists a domain
is positive (negative). If there exists a domain  containing the origin such that the function
containing the origin such that the function  is positive definite ( negative definite ) on
is positive definite ( negative definite ) on  , then the origin is an unstable point.
, then the origin is an unstable point.
Let the origin be an isolated critical point of the autonomous system. Let the function  be continous and have continuous first partial derivatives. If there is a bounded domain
be continous and have continuous first partial derivatives. If there is a bounded domain  containing the origin where
containing the origin where  for some positive
for some positive  ,
,  is positive definite and
is positive definite and  is negative definite , and then every solution of the system that starts at a point in
is negative definite , and then every solution of the system that starts at a point in  approaches the origin as
approaches the origin as  .
.
We're not told how to construct such a function. In the case of a physical system, the actual energy function would work, but in general it's more trial-and-error.
Lyapunov function
Lyapunov functions are scalar functions which can be used to prove stability of an equilibrium of an ODE.
Lyapunov's Second Method (alternative)
Notation
Definitions
Let  be a continuous scalar function.
be a continuous scalar function.
 is a Lyapunov-candidate-function if it's /locally positive-definite function, i.e.
is a Lyapunov-candidate-function if it's /locally positive-definite function, i.e.

with  bein a neighborhood region around
bein a neighborhood region around  .
.
Further, let 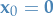 be a critical or equilibrium point of the autonomous system
be a critical or equilibrium point of the autonomous system
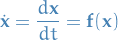
And let

Then, we say that the Lyapunov-candidate-function  is a Lyapunov function of the system if and only if
is a Lyapunov function of the system if and only if

where  denotes a specific trajectory of the system.
denotes a specific trajectory of the system.
For a given autonomous system, if there exists a Lyapunov function  in some neigborhood
in some neigborhood  of some critical / equilibrium point
of some critical / equilibrium point  , then the system is stable (in a Lyapunov sense).
, then the system is stable (in a Lyapunov sense).
Further, if  is negative-definite, i.e. we have a strict inequality
is negative-definite, i.e. we have a strict inequality

then the system is asymptotically stable about the critical / equilibrium point  .
.
When talking about critical / equilibrium point  , when considering a Lyapunov function, we have to make sure that the critical point corresponds to
, when considering a Lyapunov function, we have to make sure that the critical point corresponds to  . This can easily be achieved by "centering" the system about the point original critical point
. This can easily be achieved by "centering" the system about the point original critical point  , i.e. creating some new system with
, i.e. creating some new system with  , which will then have the corresponding critical point at
, which will then have the corresponding critical point at 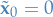 .
.
Observe that this in no way affects the qualitative analysis of the critical point.
Let  be a continuous scalar function.
be a continuous scalar function.
 is a Lyapunov-candidate-function if it's a locally postitive-definite function, i.e.
is a Lyapunov-candidate-function if it's a locally postitive-definite function, i.e.

with  being a neighborhood region around
being a neighborhood region around  .
.
Let 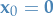 be a critical / equilibrium point of the autonomous system
be a critical / equilibrium point of the autonomous system
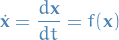
And let

be the time-derivative of the Lyapunov-candidate-function  .
.
Let  be a locally positive definite function (a candidate Lyapunov function) and let
be a locally positive definite function (a candidate Lyapunov function) and let  be its derivative wrt. time along the trajectories of the system.
be its derivative wrt. time along the trajectories of the system.
If  is locally negative semi-definite, then
is locally negative semi-definite, then  is called a Lyapunov function of the system.
is called a Lyapunov function of the system.
If there exists a Lyapunov function  of a system, then
of a system, then 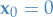 is a stable equilibrium point in the sense of Lyapunov.
is a stable equilibrium point in the sense of Lyapunov.
If in addition  and
and  for some
for some  , i.e.
, i.e.  is locally negative definite , then
is locally negative definite , then 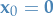 is asymptotically stable.
is asymptotically stable.
Remember, we can always re-parametrize a system to be centered around a critical point, and come to an equivalent analysis of the system about the critical point, since we're simply "adding" a constant.
Proof
First we want to prove that if  is a Lyapunov function then
is a Lyapunov function then 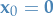 is a stable critical point.
is a stable critical point.
Suppose  is given. We need to find
is given. We need to find  such that for all
such that for all  , it follows that
, it follows that 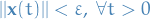 .
.
Then let  , where
, where  is the radius of a ball describing the "neighborhood" were we know that
is the radius of a ball describing the "neighborhood" were we know that  is a Lyapunov candidate function, and define
is a Lyapunov candidate function, and define

Since  is continuous, the above
is continuous, the above  is well-defined and positive.
is well-defined and positive.
Choose  satisfying
satisfying  such that for all
such that for all 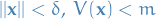 . Such a choise is always possible, again because of the continuity of
. Such a choise is always possible, again because of the continuity of  .
.
Now, consider any  such that
such that  and thus
and thus  and let
and let  be the resulting trajectory. Observe that
be the resulting trajectory. Observe that  is non-increasing, that is
is non-increasing, that is

which results in  .
.
We will now show that this implies that  , for a trajectory defined such that
, for a trajectory defined such that  and thus
and thus  as described above.
as described above.
Suppose there exists  such that
such that 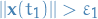 , then since we're assuming
, then since we're assuming  is such that
is such that

as described above, then clearly we also have
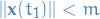
Further, by continuity (more specifically, the IVT) we must have that at an earlier time  we had
we had

But since  , we clearly have
, we clearly have

due to  . But the above implies that
. But the above implies that
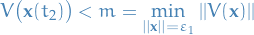
Which is a contradiction, since  implying that
implying that  .
.
Now we prove the theorem for asymptotically stable solutions! As stated in the theorem, we're now assuming  to be locall negative-definite, that is,
to be locall negative-definite, that is,
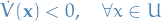
We then need to show that

which by continuity of  , implies that
, implies that  .
.
Since  is strictly decreasing and
is strictly decreasing and  we know that
we know that

And we then want to show that 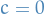 . We do this by /contradiction.
. We do this by /contradiction.
Suppose that  . Let the set
. Let the set  be defined as
be defined as

and let 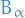 be a ball inside
be a ball inside  of radius
of radius  , that is,
, that is,
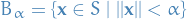
Suppose  is a trajectory of the system that starts at
is a trajectory of the system that starts at  .
.
We know that  is decreasing monotonically to
is decreasing monotonically to  and
and  for all
for all  . Therefore,
. Therefore, 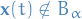 , since
, since  which is defined as all elements for which
which is defined as all elements for which  (and to drive the point home, we just established that the
(and to drive the point home, we just established that the  ).
).
In the first part of the proof, we established that

We can define the largest derivative of  as
as
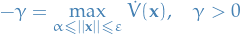
Clearly, 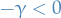 since
since  is locally negative-definite. Observe that,
is locally negative-definite. Observe that,
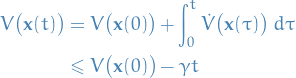
which implies that  , resulting in a contradiction established by the
, resulting in a contradiction established by the  , hence
, hence 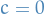 .
.
Remember that in the last step where say suppose "there exists  such that
such that 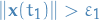 " we've already assumed that the initial point of our trajectory, i.e. for
" we've already assumed that the initial point of our trajectory, i.e. for  , was within a distance
, was within a distance  from the critical point
from the critical point  ! Thus we would have to cross the "boundary" defined by
! Thus we would have to cross the "boundary" defined by  from
from  .
.
Therefore, intuitively, we can think of the Lyapunov function providing a "boundary" which the solution will not cross given it starts with this "boundary"!
Side-notes
- When reading about this subject, often people will refer to Lyapunov stable or Lyapunov asymptotically stable , which is exactly the same as we define to be stable solutions.
Examples of finding Lyapunov functions
- Quadratic
The function
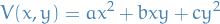
is positive definite if and only if

and is negative definite if and only if

- Example problem
Show that the critical point
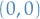 of the autonomous system
of the autonomous system
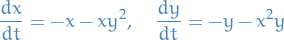
is asymptotically stable.
We try to construct a Liapunov function of the form
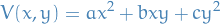
then

thus,
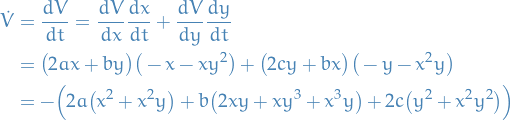
We observe that if we choose
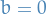 , and
, and  and
and  to be positive numbers, then
to be positive numbers, then  is negative-definite and
is negative-definite and  is positive-definite. Hence, the critical point
is positive-definite. Hence, the critical point 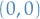 is asymptotically stable.
is asymptotically stable.
- Example problem
Partial Differential Equations
Consider the differential equation

with the boundary conditions

We call this a two-point boundary value problem.
This is in contrast to what we're used to, which is initial value problems, i.e. where the restrictions are on the initial value of the differential equation, rather than the boundaries of the differential equations.
Eigenvalues and eigenfunctions
Consider the problem consisting of the differential equation
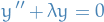
together with the boundary conditions
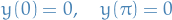
By extension of terminology from linear algebra, we call each nontrivial (non-zero) constant  an eigenvalue and the corresponding nontrivial (not everywhere zero) solution
an eigenvalue and the corresponding nontrivial (not everywhere zero) solution 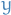 an eigenfunction.
an eigenfunction.
Specific functions
Heat equation
Models heat distribution in a row of length  .
.

with boundary conditions:

and initial conditions:

Wave equation
Models vertical displacement  wrt. horizontal position
wrt. horizontal position  and time
and time  .
.
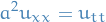
where 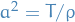 ,
,  being the tension in the string, and
being the tension in the string, and  being the mass per unit length of the string material.
being the mass per unit length of the string material.
Reasonable to have the boundary conditions:

i.e. the ends of the string are fixed.
And the initial conditions:
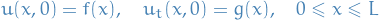
i.e. we have some initial displacement  and initial (vertical) velocity
and initial (vertical) velocity  . To keep our boundary condtions wrt.
. To keep our boundary condtions wrt.  specified above consistent:
specified above consistent:

Laplace equation

or

Since we're dealing with multi-dimensional space, we have a couple of different ways to specify the boundary conditions:
- Dirichlet problem : the boundary of the surface takes on specific values, i.e. we have a function
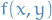 which specifies the values on the "edges" of the surface
which specifies the values on the "edges" of the surface - Neumann problem : the values of the normal derivative are prescribed on the boundary
We don't have any initial conditions in this case, as there's no time-dependence.
- Laplace's equation in cylindrical coordinates
Let
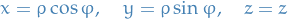
Laplace's equation becomes:
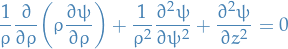
Consider BCs:
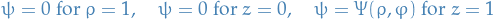
Using separation of variables:
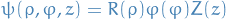
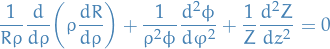
we can rewrite as:
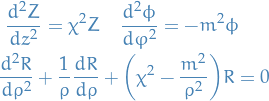
Using
 ,
,  , hence
, hence
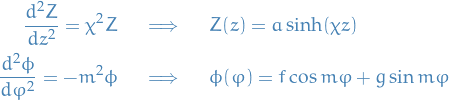
Thus, if
 , solutions are periodic.
, solutions are periodic.
The radial equation can be written in the SL-form
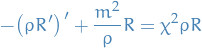
Thus,
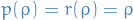 : vanish at the origin
: vanish at the origin 
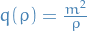 : unbounded as
: unbounded as 
Finally, making the change of variables
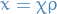 amd write
amd write  , we have
, we have
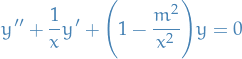
Which is the Bessel equation, and we have the general solution:

Imposing the boundary conditions:
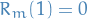
 as
as  needs to be bounded
needs to be bounded and
and  for
for 
 as
as  (due to log)
(due to log)
Hence, we require

Plotting these Bessel functions, we conclude there exists a countable infinite number of eigenvalues.
We now superpose the solutions:

to write the general solution as

The constants
 and
and  are found from the remaining BC,
are found from the remaining BC,
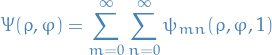
by projection on
 and
and  .
.
Orthogonality: the Besseul functions
 satisfy
satisfy
![\begin{equation*}
L[R_{mn}] = - \big( \rho R_{mn}' \big)' + \frac{m^2}{\rho} R_{mn} = \rho \xi^2 R_{mn}
\end{equation*}](../../assets/latex/differential_equations_8f950103cc7e7560fe1814d4743ed339f931637a.png)
Which has the Sturm-Liouville form, with
![\begin{equation*}
\langle L[u], v \rangle = \langle u, L[v] \rangle
\end{equation*}](../../assets/latex/differential_equations_448eef7bf1a72722a6b39f061eea76d62cd8cc89.png)
provided that
![\begin{equation*}
0 = p(x) [u'v - u v']_0^1
\end{equation*}](../../assets/latex/differential_equations_6aca78d825f931fadae55549e4945366d173260a.png)
The functions
 satisfy the above at
satisfy the above at  , where the contribution at
, where the contribution at  vanishes,
and at
vanishes,
and at  we have
we have
![\begin{equation*}
\lim_{\varepsilon \to 0} p(\varepsilon) [u'(\varepsilon)v(\varepsilon) - u(\varepsilon)v'(\varepsilon)] = 0
\end{equation*}](../../assets/latex/differential_equations_603421dd8547e6df0eaf5410be172964312ab140.png)
since
 and
and 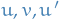 and
and  are bounded.
are bounded.
We conclude
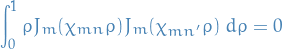
for
 . We can therefore identify the constants
. We can therefore identify the constants  and
and  by projection:
by projection:
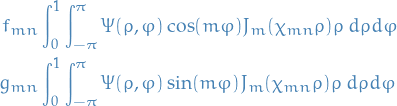
Boundary Value Problems and Sturm-Liouville Theory
Notation
![$L[y] = - [p(x) y']' + q(x) y$](../../assets/latex/differential_equations_ffa3173a593a95d2d82ccb2156f377dee8b5f737.png)
 are the ordered eigenvalues
are the ordered eigenvalues are the corresponding normalized eigenfunctions
are the corresponding normalized eigenfunctions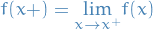 and equivalent for
and equivalent for 
Sturm-Liouville BVP
Equation of the form:
![\begin{equation*}
[p(x) y']' - q(x) y + \lambda r(x) y = 0
\end{equation*}](../../assets/latex/differential_equations_98a26130aba7476ead15479889726738075ec5c1.png)
OR equivalently
![\begin{equation*}
L[y] = \lambda r(x) y
\end{equation*}](../../assets/latex/differential_equations_03fa7e9cf8a0b1ef8849178876934fbcd61eb076.png)
with boundary conditions:

where we the boundary value problem to be regular, i.e.:
 and
and  are continuous on the interval
are continuous on the interval ![$[0, 1]$](../../assets/latex/differential_equations_68c8fa38d960e53d4308cbf1e65d04c66a554817.png)
 and
and 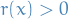 for all
for all ![$x \in [0, 1]$](../../assets/latex/differential_equations_1abcf6a6ba0996351c652ec55b2a137f25774cfc.png)
and the boundary conditions to be separated, i.e.:
- each involves only on the of the boundary points
- these are the most general boundary conditions you can have for a 2nd order differential equation
Lagrange's Identity
Let  and
and  be functions having continous second derivatives on the interval
be functions having continous second derivatives on the interval ![$x \in [0, 1]$](../../assets/latex/differential_equations_1abcf6a6ba0996351c652ec55b2a137f25774cfc.png) , then
, then
![\begin{equation*}
\int_0^1 L[u] \ v \ dx = \int_0^1 [- (pu')' v + quv ] \ dx
\end{equation*}](../../assets/latex/differential_equations_ff6cee08b44f949777f46fcd7f3ea126a06db06d.png)
where ![$L[y]$](../../assets/latex/differential_equations_649363683ef118ca5d298ad11b129363dc829bbd.png) is given by
is given by
![\begin{equation*}
L[y] = - [p(x) y']' + q(x) y
\end{equation*}](../../assets/latex/differential_equations_922b2cd49b7c861e86e8af3a1142195d7571cc2d.png)
In the case of a Sturm-Liouville problem we have observe that the Lagrange's identity gives us
![\begin{equation*}
\int_0^1 L[u] v - u L[v] \ dx = - p(x) [u'(x) v(x) - u(x) v'(x)] \Big|_0^1
\end{equation*}](../../assets/latex/differential_equations_adfd03b9802dce88d6cba9cf6ef1aba2fd9c93ac.png)
Which we can expand to
![\begin{equation*}
- p(x) [u'(x) v(x) - u(x) v'(x)] \Big|_0^1 = - p(1) [u'(1) v(1) - u(1) v'(1)] + p(0) [u'(0)v(0) - u(0)v'(0)]
\end{equation*}](../../assets/latex/differential_equations_28af542a94ae9b9e1aecb8a68273b43bc95e65ae.png)
Now, using the boundary conditions from the Sturm-Liouville problem, and assuming that  and
and  , we get
, we get
![\begin{equation*}
\begin{split}
- p(x) [u'(x) v(x) - u(x) v'(x)] \Big|_0^1 &= - p(1) \Bigg[\frac{\beta_1}{\beta_2} u(1) v(1) - u(1) \frac{\beta_1}{\beta_2} v(1) \Bigg] + \Bigg[\frac{\alpha_1}{\alpha_2} u(1) v(1) - u(1) \frac{\alpha_1}{\alpha_2} v(1) \Bigg] \\
&= 0
\end{split}
\end{equation*}](../../assets/latex/differential_equations_0afd70dadfa639f4cd067c4fcb65ddad21f905a9.png)
And if either  or
or  are zero,
are zero,  or
or  and the statement still holds.
and the statement still holds.
I.e. the Lagrange's identity under the Sturm-Liouville boundary conditions equals zero.
If 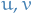 are solutions to a boundary value problem of the form def:sturm-lioville-problem, then
are solutions to a boundary value problem of the form def:sturm-lioville-problem, then
![\begin{equation*}
\int_0^1 L[u] v - u L[v] \ dx = 0
\end{equation*}](../../assets/latex/differential_equations_95d49fde485f96fd9ac6dca7cb0938401949cd8e.png)
or in the form of an inner product
![\begin{equation*}
\langle L[u], v \rangle - \langle u, L[v] \rangle = 0
\end{equation*}](../../assets/latex/differential_equations_a7ee36585ff183bc1e5808e827977a90823d5dd2.png)
If a singular boundary value problem of the form def:sturm-lioville-problem satisfies thm:lagranges-identity-sturm-liouville-boundary-conditions then we say the problem is self-adjoint. More specifically,
![\begin{equation*}
L[y] = \lambda r(x) y
\end{equation*}](../../assets/latex/differential_equations_03fa7e9cf8a0b1ef8849178876934fbcd61eb076.png)
for an n-th order operator
![\begin{equation*}
L[y] = p_n(x) \frac{d^n y}{dx^n} + \dots + p_1(x) \frac{dy}{dx} + p_0(x) y
\end{equation*}](../../assets/latex/differential_equations_64da7f6d6ce823557626d751453160e7c57a606b.png)
subject to  linear homogenous boundary conditions at the endpoints is self-adjoint provided that
linear homogenous boundary conditions at the endpoints is self-adjoint provided that
![\begin{equation*}
\langle L[u], v \rangle - \langle u, L[v] \rangle = 0
\end{equation*}](../../assets/latex/differential_equations_e95393597b3a6d1e6cdd3eca6017fd8a1da7ec29.png)
E.g. for 4th order we can have
![\begin{equation*}
L[y] = \big[ p(x) y'' \big]'' - [q(x) y']' + s(x) y
\end{equation*}](../../assets/latex/differential_equations_a8874d9e50da5a385bfabaee7d02f39dcbe9bb2a.png)
plus suitable BCs.
Most results from the 2nd order problems extends to the n-th order problems.
Some theorems
All the eigenvalues of the Sturm-Liouville problem are real.
If  and
and  are two eigenfunctions of the Sturm-Lioville problem corresponding to the eigevalues
are two eigenfunctions of the Sturm-Lioville problem corresponding to the eigevalues  and
and  , respectively, and if
, respectively, and if  , then
, then
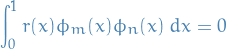
That is, the eigenfunctions  are *orthogonal to each other wrt. the weight function
are *orthogonal to each other wrt. the weight function  .
.
We note that  and
and  , with
, with  , satisfy the differential equations
, satisfy the differential equations
![\begin{equation*}
L[\phi_m] = \lambda_m r \phi_m
\end{equation*}](../../assets/latex/differential_equations_19e61c777151bfafd1abfc18e7d8e634e2a563cc.png)
and
![\begin{equation*}
L[\phi_n] = \lambda_n r \phi_n
\end{equation*}](../../assets/latex/differential_equations_2606a4e130d128c7e11e6419d49b17a749c6f95d.png)
respectively. If we let  and
and  , and substitute
, and substitute ![$L[u]$](../../assets/latex/differential_equations_0355559536e6c9a484e534051de4eef9e1a80d9b.png) and
and ![$L[v]$](../../assets/latex/differential_equations_7ba08366b1b41b349e411a74c92e6007514287a0.png) into Lagrange's Identity with Sturm-Liouville boundary conditions, we get
into Lagrange's Identity with Sturm-Liouville boundary conditions, we get
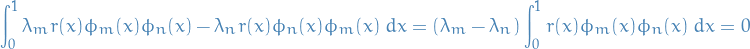
which implies that 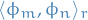 where
where  represents the inner-product wrt.
represents the inner-product wrt.  .
.
The above theorem has further consequences that, if some function  satisfies is continuous on
satisfies is continuous on ![$x \in [0, 1]$](../../assets/latex/differential_equations_1abcf6a6ba0996351c652ec55b2a137f25774cfc.png) , then we can expand
, then we can expand  as a linear combination of the eigenfunctions of the Sturm-Liouville equation!
as a linear combination of the eigenfunctions of the Sturm-Liouville equation!
Let  be the normalized eigenfunctions of the Sturm-Liouville problem.
be the normalized eigenfunctions of the Sturm-Liouville problem.
Let  and
and  be piecewise continuous on
be piecewise continuous on ![$x \in [0, 1]$](../../assets/latex/differential_equations_1abcf6a6ba0996351c652ec55b2a137f25774cfc.png) . Then the series
. Then the series

whose coefficients  are given by
are given by
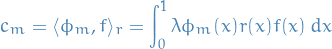
converges to ![$[f(x+) + f(x-)] / 2$](../../assets/latex/differential_equations_18cdf0058c30358feb7f6fad00bc6685449b41a5.png) at each point in the open interval
at each point in the open interval 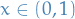 .
.
The eigenvalues of the Sturm-Liouville problem are all simple; that is, to each eigenvalue there corresponds only one linearly independent eigenfunction.
Further, the eigenvalues form an infinite sequence and can be ordered according to increasing magnitude so that

Moreover,  as
as  .
.
Non-homogenous Sturm-Liouville BVP
"Derivation"
Consider the BVP consisting of the nonhomogenous differential equation
![\begin{equation*}
L[y] = - [p(x) y']' + q(x) y = \mu r(x) y + f(x)
\end{equation*}](../../assets/latex/differential_equations_526d93dc3cd435b16042eb7835d6e609c75cb7c7.png)
where  is a given constant and
is a given constant and  is a given function on
is a given function on ![$x \in [0, 1]$](../../assets/latex/differential_equations_1abcf6a6ba0996351c652ec55b2a137f25774cfc.png) , and the boundary conditions are as in homogeonous Sturm-Lioville.
, and the boundary conditions are as in homogeonous Sturm-Lioville.
To find a solution to this non-homogenous case we're going to start by obtaining the solution for the corresponding homogenous system, i.e.
![\begin{equation*}
L[y] = \lambda r(x) y
\end{equation*}](../../assets/latex/differential_equations_03fa7e9cf8a0b1ef8849178876934fbcd61eb076.png)
where we let  be the eigenvalues and
be the eigenvalues and  be the eigenfunctions of this differential equation. Suppose
be the eigenfunctions of this differential equation. Suppose
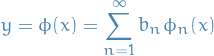
i.e. we write the solution as a linear combination of the eigenfunctions.
In the homogenous case we would now obtain the coefficients  by
by
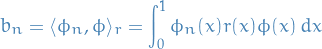
which we're allowed to do as a result of the orthogonality of the eigenfunctions wrt.  .
.
The problem here is that we actually don't know the eigenfunctions  yet, hence we need a different approach.
yet, hence we need a different approach.
We now notice that  always satisfies the boundary conditions of the problem, since each
always satisfies the boundary conditions of the problem, since each  does! Therefore we only need to deduce
does! Therefore we only need to deduce  such that the differential equation is also satisifed. We start by substituing our expansion of
such that the differential equation is also satisifed. We start by substituing our expansion of  into the LHS of the differential equation
into the LHS of the differential equation
![\begin{equation*}
L[\phi] = L \Bigg[ \sum_{n=1}^{\infty} b_n \phi_n(x) \Bigg] = \sum_{n=1}^{\infty} b_n L[\phi_n] = \sum_{n=1}^{\infty} b_n \lambda_n \phi_n(x) r(x)
\end{equation*}](../../assets/latex/differential_equations_7d3888e0c84011eb4fb78454bbdd334036437032.png)
since ![$L[\phi_n] = \lambda_n r \phi_n$](../../assets/latex/differential_equations_62cf2485194ec4c03febb3dc3a917bd243ef701c.png) from the homogenous SL-problem, where we have assumed that we interchange the operations of summations and differentiation.
from the homogenous SL-problem, where we have assumed that we interchange the operations of summations and differentiation.
Observing that the weight function  occurs in all terms except
occurs in all terms except  . We therefore decide to rewrite the nonhomogenous term
. We therefore decide to rewrite the nonhomogenous term  as
as ![$r(x) [f(x) / r(x)]$](../../assets/latex/differential_equations_e2d7a786f857163fdcaee6f8d27084af0bd84863.png) , i.e.
, i.e.
![\begin{equation*}
L[\phi] = r(x) \phi(x) + r(x) \frac{f(x)}{r(x)}
\end{equation*}](../../assets/latex/differential_equations_44cf510d5218d0e52d6fba1f3f77d50436c31974.png)
If the function  satisfies the conditions in thm:boyce-11.2.4, we can expand it in the eigenfunctions:
satisfies the conditions in thm:boyce-11.2.4, we can expand it in the eigenfunctions:

where
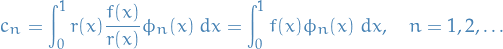
Now, substituting this back into our differential equation we get
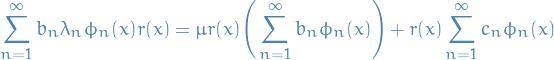
Dividing by  , we get
, we get
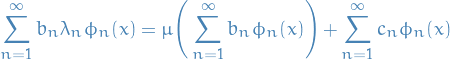
Collecting terms of the same  we get
we get

Now, for this to be true for all  , we need each of the
, we need each of the  terms to equal zero. To make our life super-simple, we assume
terms to equal zero. To make our life super-simple, we assume  for all
for all  , then
, then

and thus,
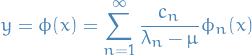
And remember, we already have an expression for  and know
and know  from the corresponding homogeonous problem.
from the corresponding homogeonous problem.
If  for some
for some  then we have two possible cases:
then we have two possible cases:
 and thus there exists no solution of the form we just described
and thus there exists no solution of the form we just described in which case
in which case  , thus we can only solve the problem if
, thus we can only solve the problem if  is orthogonal to
is orthogonal to  ; in this case we have an infinite number of solutions since the m-th coefficient can be arbitrary.
; in this case we have an infinite number of solutions since the m-th coefficient can be arbitrary.
Summary
![\begin{equation*}
L[y] = \mu \ r(x) y + f(x)
\end{equation*}](../../assets/latex/differential_equations_dd86144bf506d0aed4ef4c9504782b44ff7cf2eb.png)
with boundary conditions:

Expanding  , which means that we can rewrite the diff. eqn. as
, which means that we can rewrite the diff. eqn. as
![\begin{equation*}
\begin{split}
L[\phi] &= \mu r \phi + \sum_{i=1}^{n} c_n \phi_n r \Big( \frac{f}{r} \Big) \\
L \Big[ \sum_{i=1}^{n} b_n \phi_n \Big] &=
\end{split}
\end{equation*}](../../assets/latex/differential_equations_2fa395dfa57dbc9dbfca4eb615f1b08e2518ce53.png)
We have the solution
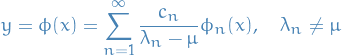
where  and
and  are the eigenvalues and eigenfunctions of the corresponding homogenous problem, and
are the eigenvalues and eigenfunctions of the corresponding homogenous problem, and
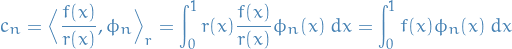
If  for some
for some  we have:
we have:
 in which case there exist no solution of the form described above
in which case there exist no solution of the form described above i which case
i which case  ; in this case we have an infinite number of solutions since the m-th coefficient can be arbitrary
; in this case we have an infinite number of solutions since the m-th coefficient can be arbitrary
Where we have made the following assumptions:
- Can rewrite the nonhomogenous part as
![$f(x) = r(x) \ [ f(x) / r(x) ]$](../../assets/latex/differential_equations_64231872871ce79f27540405ec60e365398313d1.png)
- Can expand
 using the eigenfunctions
using the eigenfunctions  wrt.
wrt.  , which requires
, which requires  and
and  to be continuous on the domain
to be continuous on the domain ![$x \in [0, 1]$](../../assets/latex/differential_equations_1abcf6a6ba0996351c652ec55b2a137f25774cfc.png)
Inhomogenous BCs Sturm-Liouville BVP
Derivation (sort-of-ish)
Consider we have at our hands a Sturm-Liouville problem of the sort:
![\begin{equation*}
\partial_{xx}^2 u - \beta^2 u = \partial_{tt}^2 u, \qquad x \in [0, a], \quad t > 0
\end{equation*}](../../assets/latex/differential_equations_6ff7fc38c4a41d467d2166bbf63581c438fee0d6.png)
for any  , satisfying the boundary conditions
, satisfying the boundary conditions
![\begin{equation*}
\begin{split}
u(0, t) = 0 &\quad u(a, t) = 0, \quad t > 0 \\
u(x, 0) = f(x), &\quad \partial_t u(x, 0) = 0, \quad \forall x \in [0, a]
\end{split}
\end{equation*}](../../assets/latex/differential_equations_3981b2b2cefa3fc6dd9c44466f3ea3944124cc52.png)
This is just a specific Sturm-Liouville problem we will use to motivate how to handle these inhomogenous boundary-conditions.
Suppose we've already obtained the solutions for the above SL-problem using separation of variables, and ended up with:

as the eigenfunctions, with the general solution:
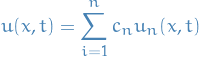
where 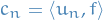 such that we satisfy the
such that we satisfy the  BC given above.
BC given above.
Then, suddenly, the examinator desires you to solve the system for a slightly different set of BCs:

What an arse, right?! Nonetheless, motivated by the potential of showing that you are not fooled by such simple trickeries, you assume a solution of the form:

where  is just as you found previously for the homogenous BCs.
is just as you found previously for the homogenous BCs.
Eigenfunctions (i.e. (countable) infinite number of orthogonal solutions)) arise only in the case of homogenous BCs, as we then still have the Lagrange's identity being satisifed. For inhomogenous BCs, it's not satisfied, and we're not anymore working with a Sturm-Liouville problem.
Nonetheless, we're still solving differential equations, and so we still have the principle of superposition available to work with.
Why would you do that? Well, setting up the new BCs:
![\begin{equation*}
\begin{split}
w(0, t) = u(0, t) + v(0, t) = T_1 &\quad w(a, t) = u(a, t) + v(a, t) = T_2, \quad t > 0 \\
w(x, 0) = u(x, 0) + v(x, 0) = f(x), &\quad \partial_t w(x, 0) = \partial_t u(x, 0) + \partial_t v(x, 0) = 0, \quad \forall x \in [0, a]
\end{split}
\end{equation*}](../../assets/latex/differential_equations_aea4ac39c8606d562523ded42d12744faffb3935.png)
Now, we can then quickly observe that we have some quite major simplifications:

If we then go on to use separation of variables for 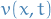 too, we have
too, we have

Substituting into the simplified BCs we just obtained:

Here it becomes quite apparent that this can only work if  , and if we simply include this constant factor into our
, and if we simply include this constant factor into our  , we're left with the satisfactory simple expressions:
, we're left with the satisfactory simple expressions:

This is neat and all, but we're not quuite ready to throw gang-signs in front of the examinator in celebration quite yet. Our expression for the additional  has now been reduced to
has now been reduced to

Substituting this into the differential equation (as we still of course have to satisfy this), we get
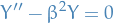
where the t-dependent factor has vanished due to our previous reasoning (magic!). Recalling that  , the general solution is simply
, the general solution is simply

Substituting into the BCs from before:

where the last BC  gives us
gives us

thus,
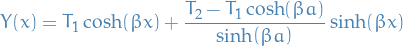
Great! We still have to satisfy the initial-values, i.e. the BCs for  . We observe that they have now become:
. We observe that they have now become:
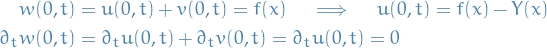
where the last t-dependent BC stays the same due to  being independent of
being independent of  . For the first BC, the implication arises from the fact that we cannot alter
. For the first BC, the implication arises from the fact that we cannot alter 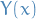 any further to accomodate the change to the complete solution, hence we alter
any further to accomodate the change to the complete solution, hence we alter  . With this alteration, we end up with the complete and final solution to the inhomogenous boundary-condition problem
. With this alteration, we end up with the complete and final solution to the inhomogenous boundary-condition problem
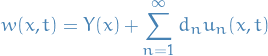
where
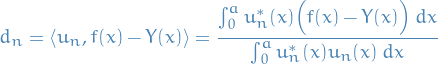
At this point it's fine to throw gang-signs and walk out.
Observe that 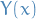 is kept outside of the sum. It's a tiny tid-bit that might be forgotten in all of this mess: we're adding a function to the general solution to the "complete" PDE, that is
is kept outside of the sum. It's a tiny tid-bit that might be forgotten in all of this mess: we're adding a function to the general solution to the "complete" PDE, that is

NOT something like this  .
.
I sort of did that right away.. But quickly realized I was being, uhmm, not-so-clever. Though I guess we could actually do it if we knew 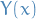 to be square-integrable! Buuut..yeah, I was still being not-so-clever.
to be square-integrable! Buuut..yeah, I was still being not-so-clever.
Example
Suppose we we're presented with a modified wave equation of the following form:
![\begin{equation*}
\partial_{xx}^2 u - \beta^2 u = \partial_{tt}^2 u, \qquad x \in [0, a], \quad t > 0
\end{equation*}](../../assets/latex/differential_equations_6ff7fc38c4a41d467d2166bbf63581c438fee0d6.png)
for any  , satisfying the boundary conditions
, satisfying the boundary conditions
![\begin{equation*}
\begin{split}
u(0, t) = 0 &\quad u(a, t) = 0, \quad t > 0 \\
u(x, 0) = f(x), &\quad \partial_t u(x, 0) = 0, \quad \forall x \in [0, a]
\end{split}
\end{equation*}](../../assets/latex/differential_equations_3981b2b2cefa3fc6dd9c44466f3ea3944124cc52.png)
and we found the general solution to be
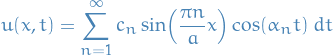
where  is as given above.
is as given above.
Now, one might wanted, what would the solution be if we suddenly decided on a set of non-homogenous boundary conditions :

To deal with non-homogenous boundary conditions, we look for a time independent solution  solving the boundary problem
solving the boundary problem

Once  is known, we determine the solution to the modified wave equation using
is known, we determine the solution to the modified wave equation using

where 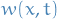 satisfies the same modified equation with different initial conditions, but homogenous boundary conditions. Indeed,
satisfies the same modified equation with different initial conditions, but homogenous boundary conditions. Indeed,
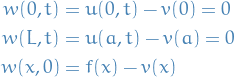
To determine  , we solve the second order ODE with constant coefficients. Since
, we solve the second order ODE with constant coefficients. Since  , its general solution is given by
, its general solution is given by
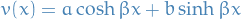
We fix the arbitrary constants using the given boundary conditions
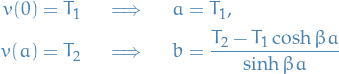
Thus, the general solution is given by

By construction, the remaining 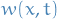 is as in the previous section, but with the coefficients
is as in the previous section, but with the coefficients  satisfying
satisfying
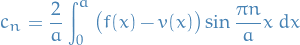
Thus, the very final solution is given by
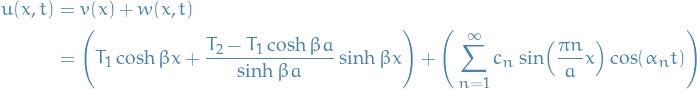
with  as given above.
as given above.
Singular Sturm-Liouville Boundary Value Problems
We use the term singluar Sturm-Liouville problem to refer to a certain class of boundary value problems for the differential equation
![\begin{equation*}
L[y] = \lambda r(x) y, \quad 0 < x < 1
\end{equation*}](../../assets/latex/differential_equations_afbe22fc9b3fbdf5025b48bb9d3a6e97f31d1933.png)
in which the functions 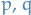 and
and  satisfy the conditions (same as in the "regular" Sturm-Liouville problem) on the open interval
satisfy the conditions (same as in the "regular" Sturm-Liouville problem) on the open interval  , but at least one of the functions fails to satisfy them at one or both of the boundary points.
, but at least one of the functions fails to satisfy them at one or both of the boundary points.
Discussion
Here we're curious about the following questions:
- What type of boundary conditions can be allowed in a singular Sturm-Liouville problem?
- What's the same as in the regular Sturm-Liouville problem?
- Are the eigenvalues real?
- Are the eigenfunctions orthogonal?
- Can a given function be expanded as a series of eigenfunctions?
These questions are answered by studying Lagrange's identity again.
To be concrete we assume 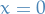 is a singular point while
is a singular point while 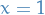 is not.
is not.
Since the boundary value problem is singular at 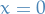 we choose
we choose  and consider the improper integral
and consider the improper integral
![\begin{equation*}
\int_{\varepsilon}^1 \{ L[u] v - u L[v] \} \ dx = - p(x) [ u'(x) v(x) - u(x) v'(x) ] \Big|_{\varepsilon}^{1}
\end{equation*}](../../assets/latex/differential_equations_2614cb9257962279df8f34af986adfd72ae137dd.png)
If we assume the boundary conditions at 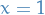 are still satisfied, then we end up with
are still satisfied, then we end up with
![\begin{equation*}
\int_{\varepsilon}^1 \{ L[u] v - u L[v] \} \ dx = p(\varepsilon) [ u'(\varepsilon) v(\varepsilon) - u(\varepsilon) v'(\varepsilon)]
\end{equation*}](../../assets/latex/differential_equations_81ea7aa8c40b8b4e7f135eaff1f2890004396608.png)
Taking the limit as  :
:
![\begin{equation*}
\int_0^1 \{ L[u] v - u L[v] \} \ dx = \underset{\varepsilon \to 0}{\lim} \ p(\varepsilon) [ u'(\varepsilon) v(\varepsilon) - u(\varepsilon) v'(\varepsilon)]
\end{equation*}](../../assets/latex/differential_equations_7aaae5dacb800f4ba4207ef4be127ed82fc5cf56.png)
Therefore, if we have
![\begin{equation*}
\underset{\varepsilon \to 0}{\lim} \ p(\varepsilon) [ u'(\varepsilon) v(\varepsilon) - u(\varepsilon) v'(\varepsilon)] = 0
\end{equation*}](../../assets/latex/differential_equations_8ed7ff5af1b3c21ff0ccfd5726c3ab6a8e4c0414.png)
we have the same properties as we did for the regular Sturm-Liouville problem!
General
In fact, it turns out that the Sturm-Liouville operator
![\begin{equation*}
L[y] = \frac{1}{w(x)} \Big( - [p(x) y'(x)]' + q(x) y(x) \Big)
\end{equation*}](../../assets/latex/differential_equations_d53905ce97c9f02c1af6838b10babe89d044beab.png)
on the space of function satisfying the boundary conditions of the singular Sturm-Liouville problem  , is a self-adjoint operator, i.e. it satisfies the Lagrange's identity on this space!
, is a self-adjoint operator, i.e. it satisfies the Lagrange's identity on this space!
And this as we have seen indications for above a sufficient property for us to construct a space of solutions to the differential equation with these eigenfunctions as a basis.
A bit more information
These lecture notes provide a bit more general approach to the case of singular Sturm-Liouville problems: http://www.iitg.ernet.in/physics/fac/charu/courses/ph402/SturmLiouville.pdf.
Frobenius method
Frobenius method refers to the method where we assume the solution of a differential equation to be analytic, i.e. we can expand it as a power series:
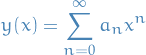
Substituting this into the differential equation, we can quite often derive recurrence-relations by grouping powers of  and solving for
and solving for  .
.
Honours Differential Equations
Equations / Theorems
Reduction of order
Go-to way
If we have some repeated roots of the characteristic equation 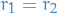 , then the general solution is
, then the general solution is

where we've taken the linear combination of the "original" solution

and the one obtained from reduction of order

General
If we know a solution  to an ODE, we can reduce the order by 1, by assuming another solution
to an ODE, we can reduce the order by 1, by assuming another solution  of the form
of the form

where  is some arbitrary function which we can find from the linear system obtained from
is some arbitrary function which we can find from the linear system obtained from  ,
, 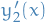 and
and  . Solving this system gives us
. Solving this system gives us

i.e. we multiply our first solution with a first-order polynomial to obtain a second solution.
Integrating factor
Assume 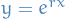 to be a solution, then in a 2nd order homogeneous ODE we get the
to be a solution, then in a 2nd order homogeneous ODE we get the

Which means we can obtain a solution by simply solving the quadratic above.
This can also be performed for higher order homogeneous ODEs.
Repeated roots
What if we have a root of algebraic multiplicity greater than one?
If the algebraic multiplicity is 2, then we can use reduction of order and multiply the first solution for this root with the  .
.
Factorization of higher order polynomials (Long division of polynomials)
Suppose we want to compute the following
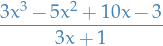
- Divide the first highest order factor of the polynomial by the highest order factor of the divisor, i.e. divide
 by
by  , which gives
, which gives 
- Multiply the
 from the above through by the divisor
from the above through by the divisor  , thus giving us
, thus giving us 
- We subtract this from the corresponding terms of the polynomial, i.e.
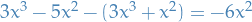
- Divide this remainder by the highest order term in of the divisor again, and repeating this process until we cannot divide by the highest order term of the divisor.
Existence and uniqueness theorem
Consider the IVP
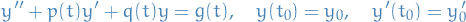
where 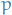 ,
,  , and
, and 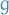 are continuous on an open interval
are continuous on an open interval  that contains the point
that contains the point  . There is exactly one solution
. There is exactly one solution 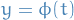 of this problem, and the solution exists throughout the interval
of this problem, and the solution exists throughout the interval  .
.
Exact differential equation
Let the functions 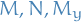 and
and  , where subscripts denote the partial derivatives, be continuous in the rectangular region
, where subscripts denote the partial derivatives, be continuous in the rectangular region  . Then
. Then

is an exact differential equation in  if and only if
if and only if

at each point of  . That is, there exists a function
. That is, there exists a function 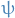 such that
such that
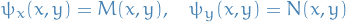
if and only if 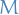 and
and  satisfy the equality above above.
satisfy the equality above above.
Variation of Parameters
Suppose we have the n-th order linear differential equation
![\begin{equation*}
L[y] = y^{(n)} + p_1(t) y^{(n - 1)} + \dots + p_{n - 1}(t) y' + p_n(t)y = g(t)
\end{equation*}](../../assets/latex/differential_equations_7b69465c5ec334852dc1292a5f0c7f52ff8f68ae.png)
Suppose we have found the solutions to the corresponding homogenous diff. eqn.

With the method of variation of parameters we seek a particular solution of the form

Since we have  functions
functions  to determine we have to specify
to determine we have to specify  conditions.
conditions.
One of these conditions is cleary that we need to satisfy the non-homongenous diff. eqn. above. Then the 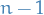 other conditions are chosen to make the computations as simple as possible.
other conditions are chosen to make the computations as simple as possible.
Taking the first partial derivative wrt.  of
of  we get (using the product rule)
we get (using the product rule)

We can hardly expect it to be simpler to determine  if we have to solve diff. eqns. of higher order than what we started out with; hence we try to surpress the terms that lead to higher derivatives of
if we have to solve diff. eqns. of higher order than what we started out with; hence we try to surpress the terms that lead to higher derivatives of  by imposing the following condition
by imposing the following condition

which we can do since we're just looking for some arbitrary functions  . The expression for
. The expression for  then reduces to
then reduces to

Continuing this process for the derivatives  we obtain our
we obtain our 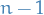 condtions:
condtions:
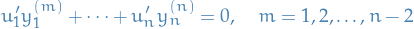
giving us the expression for the m-th derivative of  to be
to be

Finally, imposing that 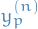 has to satisfy the original non-homogenous diff. eqn. we take the derivative of
has to satisfy the original non-homogenous diff. eqn. we take the derivative of  and substitute back into the equation. Doing this, and grouping terms involving each of
and substitute back into the equation. Doing this, and grouping terms involving each of  together with their derivatives, most of the terms drop out due to
together with their derivatives, most of the terms drop out due to  being a solution to the homogenous diff. eqn., yielding
being a solution to the homogenous diff. eqn., yielding

Together with the previous 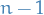 conditons we end up with a system of linear equations
conditons we end up with a system of linear equations
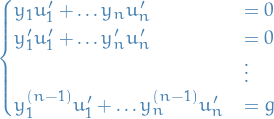
(note the  at the end!).
at the end!).
The sufficient condition for the existence of a solution of the system of equations is that the determinant of coefficients is nonzero for each value of  . However, this is guaranteed since
. However, this is guaranteed since  form a fundamental set of solutions for the homogenous eqn.
form a fundamental set of solutions for the homogenous eqn.
In fact, using Cramers rule we can write the solution of the system of equations in the form

where  is the determinant of obtained from
is the determinant of obtained from 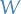 by replacing the m-th column by
by replacing the m-th column by  . This gives us the particular solution
. This gives us the particular solution
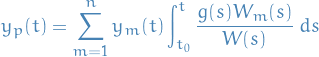
where  is arbitrary.
is arbitrary.
Suppose you have a non-homogenous differential equation of the form

and we want to find the general solution, i.e. a lin. comb. of the solutions to the corresponding homogenous diff. eqn. and a particular solution. Suppose that we find the solution of the homogenous dif. eqn. to be

The idea in the method of variation of parameters is that we replace the constants  and
and  in the homogenous solution with functions
in the homogenous solution with functions  and
and 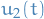 which we want to produce solutions to the non-homogenous diff. eqn. that are independent to the solutions obtained for the homogenous diff. eqn.
which we want to produce solutions to the non-homogenous diff. eqn. that are independent to the solutions obtained for the homogenous diff. eqn.
Substituting  into the non-homogenous diff. eqn. we eventually get
into the non-homogenous diff. eqn. we eventually get

which we can solve to obtain our general solution for the non-homogenous diff. eqn.
If the functions 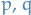 and
and 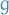 are continuous on an open interval
are continuous on an open interval  , and if the functions
, and if the functions  and
and  are a fundamental set of solutions of the homogenous differential equation corresponding to the non-homogenous differential equation of the form
are a fundamental set of solutions of the homogenous differential equation corresponding to the non-homogenous differential equation of the form

then a particular solution is

where  is any conventional chosen point in
is any conventional chosen point in  . The general solution is
. The general solution is
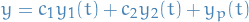
Parseval's Theorem
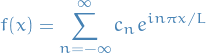
The square norm 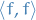 of a periodic function with convergent Fourier series
of a periodic function with convergent Fourier series
satisfies
![\begin{equation*}
\begin{split}
\langle f, f \rangle &= \int_{-L}^{L} |f(x)|^2 \ dx = 2L \sum_{n=-\infty}^{\infty} |c_n|^2 \\
&= L \Bigg[ \frac{|a_0|^2}{2} + \sum_{n=1}^{\infty} \Big( |a_n|^2 + |b_n|^2 \Big) \Bigg]
\end{split}
\end{equation*}](../../assets/latex/differential_equations_60061fb2aee1e71c45146c6c79502149abbfaceb.png)
By definition and linearity,
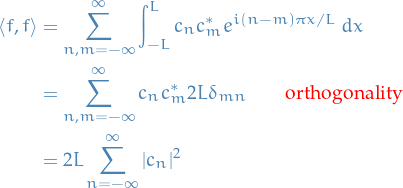
For the last equality, we just need to remember that
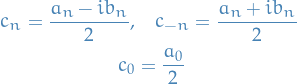
Indeed,
![\begin{equation*}
\begin{split}
2 L \sum_{n = -\infty}^{\infty} |c_n|^2 &= 2 L \Bigg[ |c_0|^2 + \sum_{n = 1}^{\infty} \Big( |c_n|^2 + |c_{-n}|^2 \Big) \Bigg] \\
&= 2 L \Bigg[ \frac{|a_0|^2}{4} + \sum_{n=1}^{\infty} \Bigg( \frac{|a_n|^2 + |b_n|^2}{4} + \frac{|a_n|^2 + |b_n|^2}{4} \Bigg) \Bigg] \\
&= L \Bigg[ \frac{|a_0|^2}{2} + \sum_{n=1}^{\infty} \Big( |a_n|^2 + |b_n|^2 \Big) \Bigg]
\end{split}
\end{equation*}](../../assets/latex/differential_equations_801f5f374d921cf944c5b8ccdf5a2cedf67a0524.png)
We also have a Parseval's Identity for Sturm-Liouville problems:
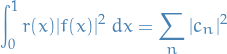
where the set  is determined as
is determined as
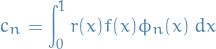
and  are the corresponding eigenfunctions of the SL-problem.
are the corresponding eigenfunctions of the SL-problem.
The proof is a simple use of the orthogonality of the eigenfunctions.
Binomial Theorem
Let  be a real number and
be a real number and  a postive integer. Further, define
a postive integer. Further, define
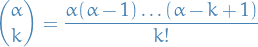
Then, if  ,
,
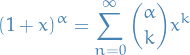
which converges for  .
.
This is due to the Mclaurin expansion (Taylor expansion about 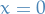 ).
).
Definitions
Words
- bifurication
- the appearance of a new solution at a certain parameter value
Wronskian
For a set of solutions  , we have
, we have
![\begin{equation*}
W[y_1, \dots, y_n] := \begin{vmatrix}
y_1 & y_2 & \dots & y_n \\
y_1' & y_2' & \dots & y_n' \\
\vdots & \vdots & \vdots & \vdots \\
y_1^{(n-1)} & y_2^{(n-1)} & \dots & y_n^{(n-1)}
\end{vmatrix}
\end{equation*}](../../assets/latex/differential_equations_1a6baed3e38084f4fd1a17f0dfda5f8b7c11d63d.png)
i.e. the Wronskian is just the determinant of the solutions to the ODE, which we can then use to tell whether or not the solutions are linearly independent, i.e. if ![$W[y_1, y_2, \dots, y_n] \ne 0$](../../assets/latex/differential_equations_547ccfe9d2e4c44ef5aeaacd2de3228bf5c66956.png) we have lin. indep. solutions and thus a unique solution for all initial conditions.
we have lin. indep. solutions and thus a unique solution for all initial conditions.
Why?
If you look at the Wronskian again, it's the determinant of the matrix representing the system of linear equations used to solve for a specific vector of initial conditions (if you set the matrix we're taking the determinant of above equal to some  which is the initial conditions).
which is the initial conditions).
The determinant of this system of linear equations then tells if it's possible to assign coefficients to these different solutions  s.t. we can satisfy any initial conditions, or more specific, there exists a unique solution for each initial condition!
s.t. we can satisfy any initial conditions, or more specific, there exists a unique solution for each initial condition!
- if
![$W[y_1, \dots, y_n] \ne 0$](../../assets/latex/differential_equations_3a57da31ba61c1c6cf702ab6b5bc8604a2a07c84.png) then the system of linear equations is an invertible matrix, and thus we have a unique solution for each
then the system of linear equations is an invertible matrix, and thus we have a unique solution for each 
- if
![$W[y_1, \dots, y_n] = 0$](../../assets/latex/differential_equations_1fbe7b9a2ece91aa570a84531d403f60032dd01c.png) we do NOT have a unique solution for each initial condition
we do NOT have a unique solution for each initial condition 
Thus we're providing an answer to the question: do the linear combination of  include all possible equations?
include all possible equations?
Properties
- If
![$W[y_1, \dots, y_n] \ne 0$](../../assets/latex/differential_equations_3a57da31ba61c1c6cf702ab6b5bc8604a2a07c84.png) then
then  \ne 0$](../../assets/latex/differential_equations_a3b2a960031335ca5954f9d40f84d17958339376.png) for all
for all ![$x \in [\alpha, \beta]$](../../assets/latex/differential_equations_1994f890f501056112a9489a992c228cca78a71b.png)
- Any solution
 can be written as a lin. comb. of any fundamental set of solutions
can be written as a lin. comb. of any fundamental set of solutions 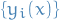
- The solutions
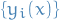 form a fundamental set iff they are linearly independent
form a fundamental set iff they are linearly independent
Proof of property 1
If  somewhere,
somewhere, 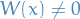 everywhere for
everywhere for ![$x \in [\alpha, \beta]$](../../assets/latex/differential_equations_1994f890f501056112a9489a992c228cca78a71b.png)
Assume  at
at 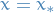
Consider
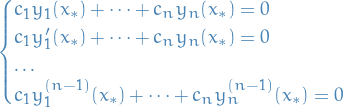
which can be written

with 
Hence,  such that (*) holds.
such that (*) holds.
Thus, we can construct  which satisfies the ODE at
which satisfies the ODE at 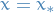
Proof of property 2
We want to show that  can satisfy any
can satisfy any
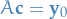
Linearly independent →  and since
and since 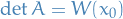 , by property 1 we can solve it.
, by property 1 we can solve it.
Homogenenous n-th order linear ODEs
![\begin{equation*}
L[y] = \frac{d^n y}{dx^n} + p_1(x) \frac{d^{n - 1} y}{dx^{n-1}} + \dots \ p_{n-1}(x) \frac{dy}{dx} + p_n(x) y = 0
\end{equation*}](../../assets/latex/differential_equations_ea2325c1a1b6bb3846562b386b302f58c2d9ea99.png)
Solutions  to homogeneous ODEs forms a vector space
to homogeneous ODEs forms a vector space
Non-homogeneous n-th order linear ODEs
![\begin{equation*}
L[y] = \frac{d^n y}{dx^n} + p_1(x) \frac{d^{n - 1} y}{dx^{n-1}} + \dots \ p_{n-1}(x) \frac{dy}{dx} + p_n(x) y = g(x)
\end{equation*}](../../assets/latex/differential_equations_5a0eecfcf96a26ffbf2e45636847b1e2528d5834.png)
Solution
- Solve the corresponding homogeneous linear ODE
- Find special case solution for the non-homogeneous
- General solution is then the linear combination of these
Power series

Laplace transform
An integral transform is a relation of the form

where  is a given function, called the kernel of the transformation, and the limits of integration
is a given function, called the kernel of the transformation, and the limits of integration  and
and  are also given.
are also given.
Suppose that
 is piecewise continuous on the interval
is piecewise continuous on the interval 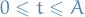 for any positive
for any positive  .
. when
when  . In this inequality,
. In this inequality,  ,
,  , and
, and  are real constants,
are real constants,  and
and 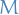 necessarily positive.
necessarily positive.
Then the Laplace transform of  , denoted
, denoted  or by
or by  , is defined
, is defined
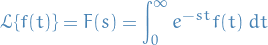
and exists for  .
.
Under these restrictions a function  which increases faster than
which increases faster than  is does not converge and thus the Laplace transform is not defined for this
is does not converge and thus the Laplace transform is not defined for this  .
.
Properties
- Identities
Let
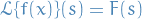 , for
, for 
- Linear operator
The Laplace transform is a linear operator:

- Uniqueness of transform
We can use the Laplace transform to solve a differential equation, and by
- Inverse is linear operator
Frequently, a Laplace transform
 is expressible as a sum of serveral terms
is expressible as a sum of serveral terms
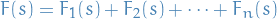
Suppose that
 . Then the function
. Then the function

has the Laplace transform
 . By the uniqueness property stated previously, no other continuous function
. By the uniqueness property stated previously, no other continuous function  has the same transform. Thus
has the same transform. Thus

that is, the inverse Laplace transform is also a linear operator.
Solution to IVP
Suppose that functions  are continuous and that
are continuous and that  is piecewise continuous on any interval
is piecewise continuous on any interval 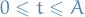 . Suppose further that
. Suppose further that

Then  exists for
exists for  and is given by
and is given by

We only prove it for the first derivative case, since this can then be expanded for the nth order derivative.
Consider the integral
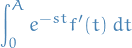
whose limit as  , if it exists, is the Laplace transform of
, if it exists, is the Laplace transform of  .
.
Suppose  is piecewise continuous, we can partition the interval and write the integral as follows
is piecewise continuous, we can partition the interval and write the integral as follows
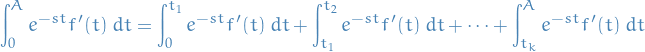
Integrating each term on the RHS by parts yields
![\begin{equation*}
\begin{split}
\int_0^A e^{-st} f'(t) \ dt =& e^{-st} f(t) \Big|_0^{t_1} + e^{-st} f(t) \Big|_{t_1}^{t_2} + \dots + e^{-st} f(t) \Big|_{k}^{A} \\
& + \Bigg[ \int_0^{t_1} e^{-st} f(t) \ dt + \int_{t_1}^{t_2} e^{-st} f(t) \ dt + \dots + \int_{t_k}^{A} e^{-st} f(t) \ dt \Bigg]
\end{split}
\end{equation*}](../../assets/latex/differential_equations_a449b0901801026f0aa88273456350b568ab6502.png)
since  is continuous, the contributions of the integrated terms at
is continuous, the contributions of the integrated terms at  cancel, and we can combine the integrals into a single integral, again due to continuity:
cancel, and we can combine the integrals into a single integral, again due to continuity:
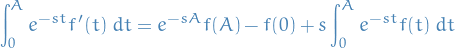
Now finally letting  (since that's what we do in the Laplace tranform ) we note that
(since that's what we do in the Laplace tranform ) we note that

And since  , we have
, we have  ; consequently
; consequently

Finally giving us
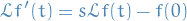
Typical ones
Fourier Series
Given a periodic function  with period
with period  , it can be expressed as a Fourier series
, it can be expressed as a Fourier series

where the coefficients are given by
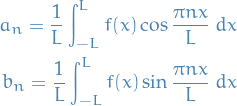
Suppose  and
and  are piecewise continuous for
are piecewise continuous for ![$x \in [-L, L]$](../../assets/latex/differential_equations_671b6022d7b856a36a3a110821724082a4610022.png) .
.
Suppose  is defined outside the interval so that it is periodic with period
is defined outside the interval so that it is periodic with period  . Then the Fourier series of
. Then the Fourier series of  converges to
converges to  where
where  is continuous and to
is continuous and to 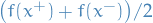 where
where  is discontinuous.
is discontinuous.
Heavside function
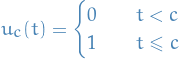
Which has a discontinuity at  .
.
Convolution integral
If  and
and  are piecewise continuous functions on
are piecewise continuous functions on  then the convolution integral of
then the convolution integral of  and
and  is,
is,
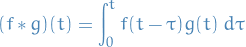
Laplace transform

Phase plane
A phase plane is a visual display of certain characteristics of certain kinds of differential equations; a coodinate plane with axes being the values of the two state variables, e.g.  .
.
It's a two-dimensional case of the general n-dimensional phase space .
Trajectory
A trajectory  of a system
of a system

simply refers to a solution for some specific initial conditions  , i.e.
, i.e.

Critical points
Points corresponding to constant solutions or equilibrium solutions, of the following equation
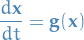
are often called critical points.
That is, points  such that
such that

There always exists a coordinate transformation  , such that
, such that
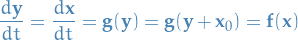
such that the new system
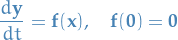
has an equilibrium solution or critical point at the origin.
Special differential equations / solutions
Legendre equation
The Legendre equation is given below:

We only need to consider  since if
since if  we can reparametrize the equation to be of the form above anyways.
we can reparametrize the equation to be of the form above anyways.
In the case where we assume  , we note that for even
, we note that for even 
 becomes a terminating series, rather than an infinite series, and if
becomes a terminating series, rather than an infinite series, and if  is odd
is odd  is a terminating series, i.e. in both cases we get a polynomial of order
is a terminating series, i.e. in both cases we get a polynomial of order  !
!
These polymomials corresponding to a solution of the Legendre equation for a specific integer  we call a Legendre Polynomial, denoted
we call a Legendre Polynomial, denoted  .
.
![\begin{equation*}
P_{\ell}(x) = \frac{1}{2^{\ell} \ell!} \frac{d^{\ell}}{dx^{\ell}} \Big[ (x^2 - 1)^{\ell} \Big]
\end{equation*}](../../assets/latex/differential_equations_940cb67f32f04309801cd7081d71273f5ab675ac.png)
Or the general Legendre equation :
![\begin{equation*}
(1 - x^2) y'' - 2x y' + \Bigg[ \ell (\ell + 1) - \frac{m^2}{1 - x^2} \Bigg] y = 0
\end{equation*}](../../assets/latex/differential_equations_fc1168ae92c05fcb50130305913184fac581ff1c.png)
Which gives rise to the polynomials defined
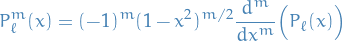
where  are the corresponding Legendre polynomial.
are the corresponding Legendre polynomial.
Moreover, using Rodrigues formula
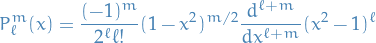
If we let  we can use the relationship between
we can use the relationship between 

to obtain the coefficient
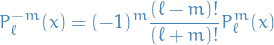
Series Solutions
The sum of the even terms is given by:
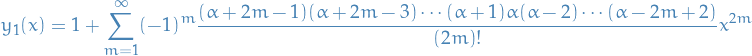
and the sum of the odd terms are given by:

TODO Legendre polynomials and Laplace equation using spherical coordinates
Van der Pol oscillator
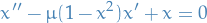
where  is the position coordinate, which is a function of time
is the position coordinate, which is a function of time  , and
, and  is a scalar parameter indicating the nonlinearity and the strength of the damping.
is a scalar parameter indicating the nonlinearity and the strength of the damping.
Hermite polynomials
We are talking about the physicsts' Hermite polynomials given by
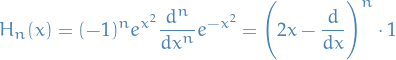
These are a orthonormal polynomial sequence, and they arise from the differential equation

These polynomials are orthogonal wrt. the weight function  , i.e. we have
, i.e. we have
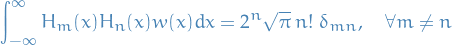
Furthermore, the Hermite polynomials form an orthogonal basis of a the Hilbert space of functions satisfying

in which the inner product is given by the integral including the Gaussian inner product defined previously:
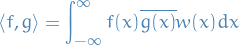
Spherical harmonics
In this section we're looking to tackle the spherical harmonics once and for all.
If we have a look at the Laplace equation in spherical coordinates, we have

If we then use separation of variables, and consider solutions of the form:

We get the following differential equations:
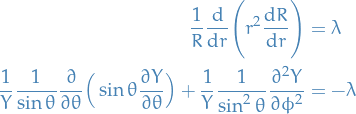
Further, assuming  , we can rewrite the second differential equation as
, we can rewrite the second differential equation as
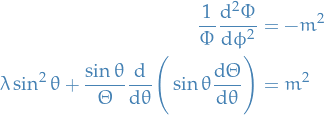
for some number  .
.
Solving for 
First we take a look at the differential equation involving  ,
,

Which we can rewrite as
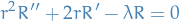
making the substitution

This is fine, since in spherical coordinates we have  , i.e.
, i.e.  is always defined.
is always defined.
Thus,
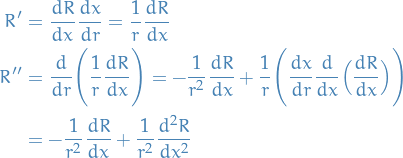
Substituting back into the differential equation, we get
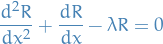
which has the general solution
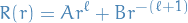
where
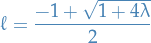
solves

or rather,
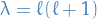
RECOGNIZE THIS YO?! How about trying to substitute this into the differential equation involving  ?
?
Solving for 
The differential equation with  can be written
can be written

which has the solution

Further, we have the boundary condition  , which implies
, which implies  .
.
Solving for 
We have the the ODE
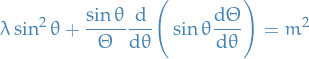
which we can write out to get

Making the substitution  we have
we have
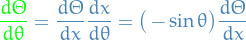
And,
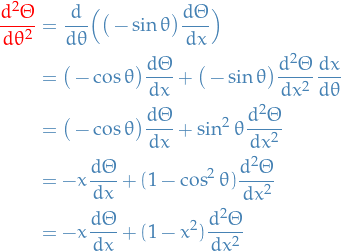
Substituting back into the ODE from above:
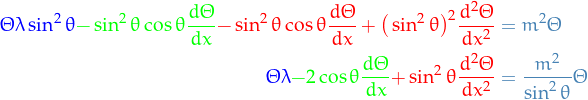
Observing that
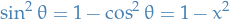
We can write the above equation as
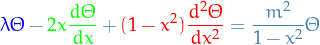
Whiiiich, we recognize as the general Legendre differential equation!
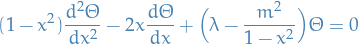
where we're only lacking the 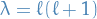 , for which we have to turn to the differential equation involving
, for which we have to turn to the differential equation involving  .
.
With 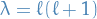 obtained from Solving for
obtained from Solving for  , we can rewrite the differential equation involving
, we can rewrite the differential equation involving  as
as
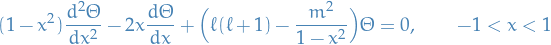
For which we know that the solutions are the corresponding associated Legendré polynomials
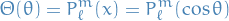
which are obtained by considering the series solution of the equation above, i.e. assuming:
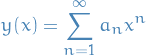
where  is as above. Substituting into the differential equation above, and finding the recurrence-relation for
is as above. Substituting into the differential equation above, and finding the recurrence-relation for  we recover the Legendre polynomials mentioned above.
we recover the Legendre polynomials mentioned above.
Bringing  and
and  together
together
Now, finally bringing this together with the solution obtained for  , we have the spherical harmonics
, we have the spherical harmonics

where  is simply the normalization constant to such that the eigenfunctions form a basis, which turns out to be
is simply the normalization constant to such that the eigenfunctions form a basis, which turns out to be
Thus, the final expression for the spherical harmonics is
Combining everything
Finally, combining the radial solution and the spherical harmonics into the final expression for our solutions:
where we have set 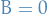 to ensure regularity at
to ensure regularity at  , and not have the following occur:
, and not have the following occur:

Boundary conditions
- Establish that
 must be periodic (since we're working in spherical coordinates) whose period evenly divides
must be periodic (since we're working in spherical coordinates) whose period evenly divides  , which implies
, which implies  and
and  is a linear combination of
is a linear combination of 
- Using what we observed in 1. and noting that
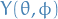 is "regular" at the poles of the sphere, where
is "regular" at the poles of the sphere, where  , we have a boundary condition for
, we have a boundary condition for  (which is a Sturm-Liouville problem) forcing the parameter
(which is a Sturm-Liouville problem) forcing the parameter  to be of the form
to be of the form 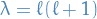
- Making the change of variables
 trnasforms this equation into the general Legendre equation, whose solution is a multiple of the associated Legendre Polynomial.
trnasforms this equation into the general Legendre equation, whose solution is a multiple of the associated Legendre Polynomial. Finally, the equation for
 has solutions of the form
has solutions of the form

- If we want the solution to be "regular" throughout
 , we have
, we have 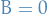 .
.
When we say regular, we mean that the solution  has the property
has the property

Proper description
A priori  is a complex number, BUT because
is a complex number, BUT because  must be a periodic function whose period evenly divides
must be a periodic function whose period evenly divides  ,
,  is necessarily an integer and
is necessarily an integer and  is a linear combination of the complex exponentials
is a linear combination of the complex exponentials  .
.
Further, the solution function 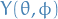 is regular at the poles of the sphere, where
is regular at the poles of the sphere, where  . Imposing this regularity in the solution
. Imposing this regularity in the solution  of the second equation at the boundary of the domain is a Sturm-Liouville problem that forces the parameter
of the second equation at the boundary of the domain is a Sturm-Liouville problem that forces the parameter  to be of the form
to be of the form
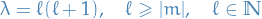
Furthermore, a change of variables  transforms this equation into the (general) Legendre equation, whose solution is a multiple of the associated Legendre polynomial
transforms this equation into the (general) Legendre equation, whose solution is a multiple of the associated Legendre polynomial 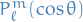 .
.
Finally, the equation for  has solutions of the form
has solutions of the form
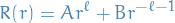
And if we require  solution to be regular throughout
solution to be regular throughout  forces
forces 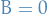 .
.
Solutions
Here, the solution assumed to have the special form  . For a given value of
. For a given value of  , there are
, there are  independent solutions of this form, one for each integer
independent solutions of this form, one for each integer  . These angular solutions are a product of trigonometric functions, here represented as a complex exponential, and associated Legendre polynomials:
. These angular solutions are a product of trigonometric functions, here represented as a complex exponential, and associated Legendre polynomials:

which fulfill

The general solution to the Laplace's equation in a ball centered at the origin is a linear combination of the spherical harmonic functions multiplied by the appropriate scale factor  ,
,
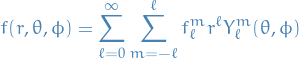
where the 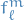 are constants the factors
are constants the factors  are known as solid harmonics.
are known as solid harmonics.
Q & A
DONE Why do we actually require the  to be an integer?
to be an integer?
In solving for  we observe that
we observe that

Thus, if we require  to be true, then we need
to be true, then we need  to "go full circle" every
to "go full circle" every  , hence
, hence  .
.
If it does NOT go full circle, then it would be discontinuous.
DONE We have TWO explanations for why we need 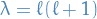 , which one is true?
, which one is true?
- Question
Here we state that
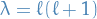 has to be "because it's a Sturm-Liouville problem". I don't understand why it being a Sturm-Liouville problem necessarily imposes this restriction.
has to be "because it's a Sturm-Liouville problem". I don't understand why it being a Sturm-Liouville problem necessarily imposes this restriction.
Ah! Maybe it's because Sturm-Liouville problems require the limiting behavior of the boundary conditions to satisfy Lagrange's identity being zero!
While here, we simply solve the differential equation involving
 , and
, and 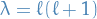 just falls out from this solution, and as far as I can tell, we're not actually saying anything about the boundary conditions in this case.
just falls out from this solution, and as far as I can tell, we're not actually saying anything about the boundary conditions in this case.
- Answer
From what I can understand, the eigenvalue
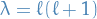 simply falls out from
simply falls out from  as we found, and
as we found, and  being of this form does not seem to be related in any way to boundary conditions.
being of this form does not seem to be related in any way to boundary conditions.
What is related to the boundary conditions, the fact that
 is an integer.
is an integer.
What is related to the b
Bessel equation
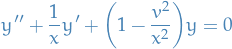
This can be solved using Frobenius method.
In the case where  , we end up with the Bessel function of the 1st kind :
, we end up with the Bessel function of the 1st kind :

And the Bessel function of the 2nd kind :
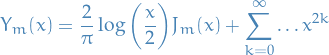
Thus, the general solution will be the linear combination:

Where we have the following limiting behavior:
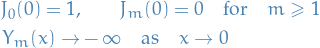
Note: Quite often we want the solution to be "regular" / nicely behaved as  , thus we often end up setting
, thus we often end up setting  in the expression for
in the expression for  .
.
Problems
10.2 Fourier Series
Ex. 10.2.1
Assume that there is a Fourier series converging to the function  defined by
defined by
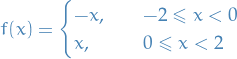
with the property that

i.e. it's periodic with a period of 4.
Find the components of the Fourier series.
Solution
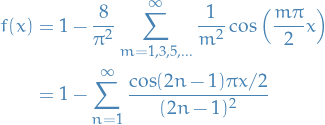
See p. 601 in (Boyce, 2013) for the full solution.
10.5 Separation of variables; Heat conduction in a Rod
Find the solution of the heat conduction problem
 1
1
Solution

We suppose

And the boundary conditions are satisfied by
First we note that with  above we get the following
above we get the following

which gives
for some constant  , which gives us the system
, which gives us the system
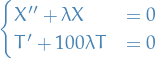
The solution to the first equation simply gives us
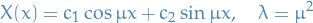
Considering the boundary conditions, we get
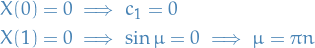
thus we get the eigenfunctions and eigenvalues for  :
:

Substituting these eigenvalues into the differential equation with  :
:

which can be solved by use of integrating factors, thus
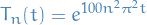
Finally, combining both into the eigenfunctions for the entire solution 

Which gives us the general solution:
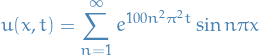
and solving for the coefficients using the initial conditions, i.e. when 
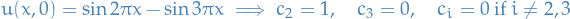
Hence the final solution is
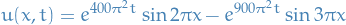

 is some specific solution to the non-homogenous equation.
is some specific solution to the non-homogenous equation.

 and
and  for
for  :
: