Complex Analysis
Table of Contents
Definitions
A multivalued function is a function which assigns to each point a set of values rather than a single value to each point, as a regular function would.
We define the open ball (or open disk since the complex plane is 2-dimensional) in the same way we do for the reals:
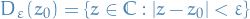
and the closed disk

Open and closed sets in the complex plane then follow the same definition as for open and closed sets in the 2-dimension real case.

Functions
The *complex exponential function is the function 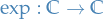 defined by
defined by
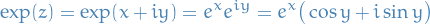

and

Let  be non-zero. We define the multivalued function
be non-zero. We define the multivalued function  by
by
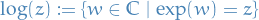
We call any element  of
of  a logarithm of
a logarithm of  .
.
The principal branch of the logarithm function is the function  defined by
defined by

for non-zero  , where
, where  is the principal value of the argument function.
is the principal value of the argument function.
Or more general
The branch cut of a complex function is defined to be the point in the principal branch where the function is no longer holomorphic.
Theorems
Holomorphic functions
Notation
 is almost always denoted
is almost always denoted 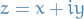

![$\text{Arg}(z) = \{ \theta : z = |z| e^{i \theta}, \quad \theta \in (- \pi, \pi] \}$](../../assets/latex/complex_analysis_707f97fdf09908b321f7128de315cad9693b846c.png) , i.e. the unique
, i.e. the unique  in the range
in the range ![$(- \pi, \pi]$](../../assets/latex/complex_analysis_39e75a4054865907d644b69b92146a780d427253.png)
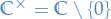 is the complex plane without origin => can be equipped with multiplication operation to form an (Abelian) group
is the complex plane without origin => can be equipped with multiplication operation to form an (Abelian) group- complex-valued function of a real variable means
 , i.e. input is real and we can decompose the output into a real part and an imaginary part
, i.e. input is real and we can decompose the output into a real part and an imaginary part 
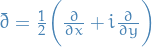
Differential Geometric view on arg function
Let

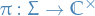 defined by
defined by  , which is then surjective and continuous
, which is then surjective and continuous
Apparently, we call a complex manifold such as the one above a Riemann surface, and I honestly believe this is something I ought to return to once I have a better understanding of what complex manifolds are.
Observe then that this defines a fibre bundle, since for any two points  we have the fibres be isomorphic, i.e.
we have the fibres be isomorphic, i.e.  .
.
 is the plane defined by Cartesian product
is the plane defined by Cartesian product  since
since  and
and  . Thus,
. Thus,  is in fact a topological manifold (probably equipped with the standard topology, but I haven't checked). Further we observe that
is in fact a topological manifold (probably equipped with the standard topology, but I haven't checked). Further we observe that  is also a topological manifold. Thus, we our fibre bundle as claimed earlier.
is also a topological manifold. Thus, we our fibre bundle as claimed earlier.
Complex-valued functions
Suppose we have a complex-valued function of a real value
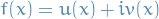
We then say that  is continuous at
is continuous at  if and only if both
if and only if both  and
and  are continuous at
are continuous at  .
.
If  is instead a complex-valued function of a complex variable, let
is instead a complex-valued function of a complex variable, let 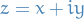 , then
, then
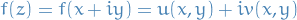
We then say that  is continuous at
is continuous at  if and only if for any
if and only if for any  there exists
there exists  s.t.
s.t.

where  and
and  are real valued functions, and this is thus equivalent of
are real valued functions, and this is thus equivalent of  and
and  being continuous at the point
being continuous at the point  .
.
Complex differentiability and holomorphicity
A function  in a neighborhood
in a neighborhood  of
of  is differentiable (everywhere in
is differentiable (everywhere in  ) if and only if its real and imaginary parts
) if and only if its real and imaginary parts  and
and  are continuously differentiable and obey the Cauchy-Riemann equations (everywhere in
are continuously differentiable and obey the Cauchy-Riemann equations (everywhere in  ):
):

This can be seen by considering the "normal" definition of differentiability at a point, and observing the definition changes depending on which direction we approach the point from (vertical or horizontal direction).
Important: it's crucial that the function be differentiable in a neighborhood  of
of  not just at the point
not just at the point  !
!
We say that the complex-valued function  is holomorphic at
is holomorphic at  if it is differentiable everywhere in some neighbourhood
if it is differentiable everywhere in some neighbourhood  of
of  .
.
We say that a function is entire if it is holomorphic in the whole complex plane.
Let 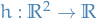 .
.
Then  is harmonic if it satisfies the Laplace equation:
is harmonic if it satisfies the Laplace equation:
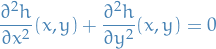
Let  be open, and let
be open, and let  be harmonic.
be harmonic.
We say a harmonic function  is the harmonic conjugate of
is the harmonic conjugate of  if the complex-valued function
if the complex-valued function

is holomorpic on  .
.
Solving differential equations
This techinque can be used to solve differential equations on "ugly" domains.
Consider the following:
Polynomials and rational functions
Complex powers
Let 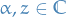 with
with  . Then we define
. Then we define  th power of
th power of  by
by
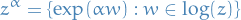
Unless stated otherwise, a complex power is defined in the principal branch.
Let 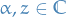 with
with  . Then
. Then
- if
 there is exactly one value of
there is exactly one value of 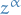
- if
 where
where 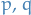 are coprime, with
are coprime, with  there are exactly
there are exactly  values of
values of 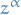
- if
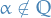 or
or  , there are infinitely manu values of
, there are infinitely manu values of 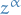
Let  . Then the
. Then the  values
values

where

are the  roots of unity.
roots of unity.
Graphing complex functions
- Hard to visualize as 2D + 2D becomes 4D
- Good idea to treat each of the different 3D plots separately
Let  be open, and let
be open, and let  .
.
We say  is conformal if
is conformal if  preserves angles: i.e. if the angle between the images under
preserves angles: i.e. if the angle between the images under  of two straight lines in
of two straight lines in  are equal to the angle between the two straight lines themselves.
are equal to the angle between the two straight lines themselves.
By applying this definition to tangents of differentiable curves, more generally we can say the same about the angles between curves at certain points.
We're saying the push-forward of 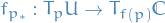 , is angle-preserving.
, is angle-preserving.
Therefore, any diffeomorphism between  and
and  is angle-preserving.
is angle-preserving.
Consider 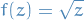 . For
. For  ,
,  . Then we consider the surface
. Then we consider the surface
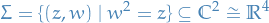
and the function
 defined by
defined by 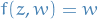 .
.
- This is the projection of a bundle; further,
 forms a fibre bundle (right?)
forms a fibre bundle (right?)
Let  be open, and let
be open, and let  be holomorphic.
be holomorphic.
Then  preserves angles at every
preserves angles at every  where
where  .
.
This theorem is useful for establishing the image of a function (if it's a polytope (?)) since we can simply compute the mapped values at the edges (i.e. curves from vertex to vertex) and, knowing that the angles are preserved, immediately know how the edges between the mapped vertices look.
Möbius transformations
A Möbius transformation is a function of the form
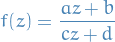
where 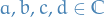 are such that
are such that  .
.
Observe that  is not defined on the entirety of
is not defined on the entirety of  , which leads us to defining the extended complex plane.
, which leads us to defining the extended complex plane.
We'll often consider the case  , if nothing else is specified.
, if nothing else is specified.
That is, a Mobius transformation is defined on 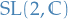 .
.
The extended complex plane is the set  , where
, where  is just some object
is just some object 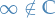 .
.
We extend the usual arithmetic operations in the following way: for  and non-zero
and non-zero  ,
,
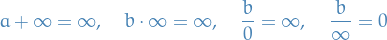
Consider the coordinates  describing
describing  . We identify the complex plane with the plane defined by
. We identify the complex plane with the plane defined by  , and a complex number
, and a complex number  with the point
with the point  .
.
The Riemann sphere is the unit sphere  in
in  defined by
defined by

and we consider the "north pole" to be the point  .
.
The Riemann sphere therefore has two charts:
- For all points in the complex plane, the chart is the identity map from the sphere (with
 removed) to the complex plane.
removed) to the complex plane. - For
 , the chart neighborhood is the sphere (with the origin removed), and the chart is given by sending
, the chart neighborhood is the sphere (with the origin removed), and the chart is given by sending  to
to  and all other points
and all other points  to
to  .
.
Let 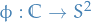 such that the three points
such that the three points  ,
,  , and
, and  are colinear.
are colinear.
It is clear that
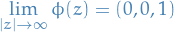
thus we define also  and thereby consider
and thereby consider  as being defined on the extended complex plane, i.e.
as being defined on the extended complex plane, i.e. 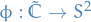 .
.
The map 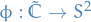 is evidently bijective, so it has an inverse
is evidently bijective, so it has an inverse 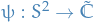 . This function
. This function 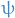 is the sterographic projection.
is the sterographic projection.
Better description:
The unit sphere in  is the set of pints
is the set of pints  such that
such that 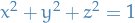 .
.
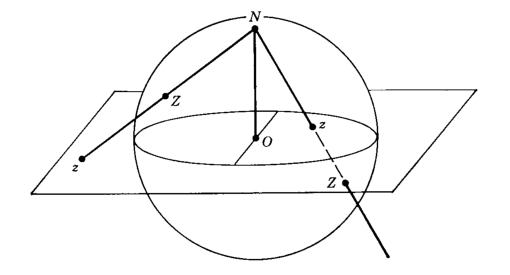
Let  be the "north pole", and let
be the "north pole", and let  be the rest of the sphere.
be the rest of the sphere.
The plane 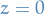 (xy-plane) runs through the center of the sphere; the "equator" is the intersection of the sphere with this plane.
(xy-plane) runs through the center of the sphere; the "equator" is the intersection of the sphere with this plane.
For any point  on
on  , there is a unique line through
, there is a unique line through  and
and  , and this line intersects the plane
, and this line intersects the plane 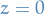 in exactly one point
in exactly one point 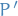 . We define the stereographic projection of
. We define the stereographic projection of  to be this point
to be this point 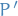 in the plane.
in the plane.
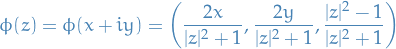
and
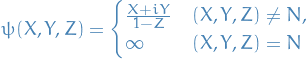
Stereographic projection maps a circle to either a circle or a straight line (a "circline").
Makes some people say that straight lines are circles of infinite radius.
A translation is a Möbius transformation of the form

which corresponds to the matrix
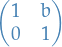
A rotation is a Möbius transformation of the form

so that
 for some
for some  , which corresponds to the matrix
, which corresponds to the matrix
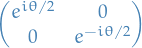
A dilation is a Möbius transformation of the form

which corresponds to the matrix
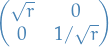
An inversion is a Möbius transformation of the form
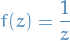
which corresponds to the matrix

We say that a Möbius transformation  fixes the point of infinity if
fixes the point of infinity if  .
.
Translations, rotatons, and dilations fix the point at infinity, while inversions do not.
Let  be a Möbius transformation. Then
be a Möbius transformation. Then  is a composition of a finite number of translations, rotations, diluations, and, if and only if
is a composition of a finite number of translations, rotations, diluations, and, if and only if  does not fix the point at infinity, one inversion.
does not fix the point at infinity, one inversion.
Möbius transformations map circlines to circlines.
Let  be three distinct points. Then there exists a unqiue Möbius transformation
be three distinct points. Then there exists a unqiue Möbius transformation  such that
such that

This is useful because we by simply knowing how the Möbius transformation maps the three different points, we can tell what it does to circles or lines.
Let  be distinct points.
be distinct points.
The cross-ratio ![$[z_1, z_2, z_3, z_4]$](../../assets/latex/complex_analysis_e06d800ca270832355c362196848f53ea64fb414.png) of the four points is the image of
of the four points is the image of  under the Möbius transformation which sends
under the Möbius transformation which sends  to
to 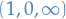 .
.
Complex integration
Complex integrals
Let ![$[a, b] \subseteq \mathbb{R}$](../../assets/latex/complex_analysis_bd1ba0aac216874a2e2146f6e486a6eb65a45dff.png) be a interval, and
be a interval, and ![$f : [a, b] \to \mathbb{C}$](../../assets/latex/complex_analysis_ddb30433117f2e72dee9eb1c12be8b4ac672b7b5.png) of the form
of the form

Then  is integrable if its real and imaginary parts
is integrable if its real and imaginary parts ![$u, v: [a, b] \to \mathbb{R}$](../../assets/latex/complex_analysis_26abfca43faa7a112dcd60889e468a7634d47463.png) are integrable in the usual (real) sense, and we define the integral of
are integrable in the usual (real) sense, and we define the integral of  by
by

It will usually suffice to observe that continuous functions are integrable.
Example
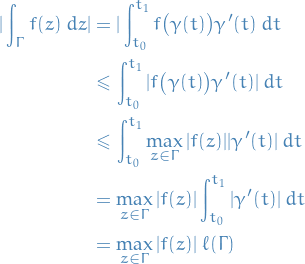
where  denotes the arc-length of
denotes the arc-length of  .
.
 is by def. closed and bounded, i.e. a compact set
is by def. closed and bounded, i.e. a compact set is continuous
is continuous
Hence  is in fact bounded i.e. finite.
is in fact bounded i.e. finite.
Contour integrals
Let  be distinct.
be distinct.
Then a (parametrized) curve  connecting
connecting  and
and  is a continuous function
is a continuous function
![\begin{equation*}
\begin{split}
\gamma : [t_0, t_1] \to \mathbb{C}, & \quad t_0, t_1 \in \mathbb{R}, \quad t_0 < t_1 \\
\text{such that} & \quad \gamma(t_0) = z_0, \quad \gamma(t_1) = z_1
\end{split}
\end{equation*}](../../assets/latex/complex_analysis_8369f820d71cf1365de5edc841af4833e39672d1.png)
Writing  and
and  , we decompose
, we decompose  into a real and imaginary parts for continuous real functions
into a real and imaginary parts for continuous real functions ![$x, y: [t_0, t_1] \to \mathbb{R}$](../../assets/latex/complex_analysis_aaffa43c022faeb05b95cdc4895d571455fdbfcd.png) , so
, so
![\begin{equation*}
\gamma(t) = x(t) + i y(t), \quad \forall t \in [t_0, t_1]
\end{equation*}](../../assets/latex/complex_analysis_8f5f60e424b927d41f41a4abf91d949195644368.png)
We say the curve  is regular if
is regular if  is continuously differentiable and
is continuously differentiable and  forall
forall ![$t \in [t_0, t_1]$](../../assets/latex/complex_analysis_34d0e8fd18f3d6a92d38457e27afc3052c8014ce.png) .
.
A curve  from
from  to
to  in
in  is a contour if it is a finite union of regualr curves, which together joint
is a contour if it is a finite union of regualr curves, which together joint  with
with  , i.e. there exists
, i.e. there exists
![\begin{equation*}
\gamma_i : [t_0^i, t_1^i] \to \mathbb{C}, \quad i = 1, \dots, n
\end{equation*}](../../assets/latex/complex_analysis_a3cc1eabc7d380b9116d61b465045deddae09378.png)
such that
![\begin{equation*}
\gamma(t) =
\begin{cases}
\gamma_1(t) & \quad \text{if } t \in [t_0, t_1] \\
\gamma_2(t) & \quad \text{if } t \in [t_1, t_2] \\
& \vdots \\
\gamma_n(t) & \quad \text{if } t \in [t_{n - 1}, t_n]
\end{cases}
\end{equation*}](../../assets/latex/complex_analysis_e9b33701e751d9a052a3d068700b49cf8ee72cfd.png)
such that  is continuous.
is continuous.
For a continuous function  , we define the contour integral of
, we define the contour integral of  along
along  by
by
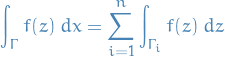
Let  be a curve in
be a curve in  , and let
, and let  be continuous. Then
be continuous. Then

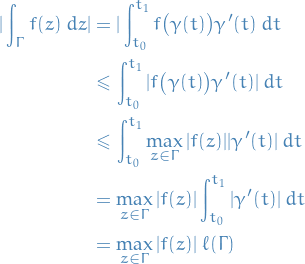
Let  . We will say that
. We will say that  is a domain if
is a domain if  is open and every two points in
is open and every two points in  can be connected by a contour which lies wholly on
can be connected by a contour which lies wholly on  .
.
Let  be a domain, and
be a domain, and  be continous. Then the following are equivalent:
be continous. Then the following are equivalent:
 has an antiderviative
has an antiderviative  on
on 
 for all closed contours
for all closed contours  in
in 
- all contour integrals
 are independent of path
are independent of path  , and depend only on the endpoints.
, and depend only on the endpoints.
Cauchy's Integral Theorem
Let  be a contour in
be a contour in  .
.
Then  is simple if it has no self-intersections, except possible at the endpoints, i.e.
is simple if it has no self-intersections, except possible at the endpoints, i.e.  for all distinct
for all distinct ![$s, t \in [t_0, t_1]$](../../assets/latex/complex_analysis_ab93adf0cdfb6aae2ffeed1a6f5e97f7b3fd329e.png) , unless
, unless  and
and  and
and  is a closed contour.
is a closed contour.
A loop is a simple, closed contour.
Let  be a loop in
be a loop in  . Then
. Then  defines two regions in the
defines two regions in the  , with
, with  as their common boundary:
as their common boundary:
- a boundary domain, the interior of

- an unbounded domain, the exterior of

Let  be a loop in
be a loop in  . We say
. We say  is positively-oriented if as we move along the curve in the direction of parametrization, the interior is on the LHS.
is positively-oriented if as we move along the curve in the direction of parametrization, the interior is on the LHS.
Otherwise state, all loops should be assumed to be positively-oriented.
 is said to be simply connected if the interior of every loop on
is said to be simply connected if the interior of every loop on  lies wholly in
lies wholly in  .
.
Let  and
and  be a loop in
be a loop in  which does not pass through
which does not pass through  . Then
. Then

Since  , we clearly have two cases:
, we clearly have two cases:
 : integral is zero due to Cauchy Integral theorem
: integral is zero due to Cauchy Integral theorem : Consider the following figure:
: Consider the following figure:
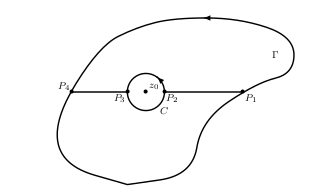 Since
Since  this figure basically "encapsulates" all possible loops which have
this figure basically "encapsulates" all possible loops which have  outside!
outside!
We break the integrand  , aswell as the differential
, aswell as the differential  into their real and imaginary components:
into their real and imaginary components:
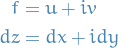
In this case we have
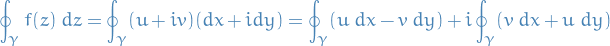
By Green's Theorem, we may then replace the integrals around the closed contour  with an area integral throughout the domain
with an area integral throughout the domain  that is enclosed by
that is enclosed by  as follows:
as follows:
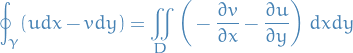
and for imaginary part,
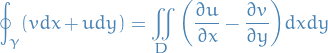
However, being the real and imaginary parts of a function holomorphic in the domain  ,
,  and
and  must satisfy the Cauchy-Riemann equations there:
must satisfy the Cauchy-Riemann equations there:
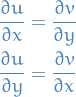
We therefore find that both integrads (and hence their integrals) are zero:
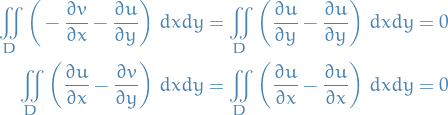
Which gives us the result

as wanted.
Let  be a loop,
be a loop,  , and
, and  be holomorphic inside and on
be holomorphic inside and on  . Then
. Then

Let  be a loop,
be a loop,  be holomorphic inside and on
be holomorphic inside and on  , and
, and  lie inside
lie inside  .
.
Then  is infinitively differentiable at
is infinitively differentiable at  and, for all positive integers
and, for all positive integers  ,
,

Liouville's Theorem and its applications
Let  be a domain,
be a domain,  and
and  be such that
be such that  ,
,  be holomorphic on
be holomorphic on  , and
, and  be such that
be such that  for all
for all  .
.
Then for all  , we have that
, we have that

Maximum Modulus Principle
 and
and  be such that the closed disc
be such that the closed disc  , and
, and  be holomorphic on
be holomorphic on  .
.
Then
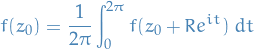
Let:
 be holomorphic on a domain
be holomorphic on a domain 

 s.t.
s.t. 
Fix  , then
, then
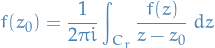
where  is the circle of radius
is the circle of radius  centred at
centred at  (Cauchy Integral formula).
(Cauchy Integral formula).
 is parametrized by
is parametrized by ![$\gamma: [0, 1] \to \mathbb{C}$](../../assets/latex/complex_analysis_05db2e2a2ee4e42064bcf8a0eb123966096343f4.png) , given by
, given by

So, using the definition of the contour integral
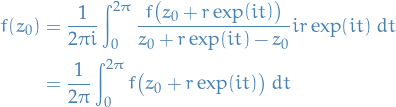
Suppose

i.e. maximum value is attained at the center of the circle. Then,
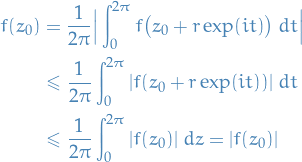
hence
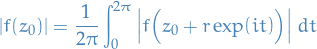
which, since 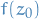 is clearly constant, we can use the linearity of the integral to get
is clearly constant, we can use the linearity of the integral to get
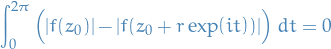
which is a non-negative continuous function, which implies that the expression inside the integral is zero for all ![$t \in [0, 2\pi]$](../../assets/latex/complex_analysis_56b1489746a1989d9507a6a3268ec55d836d226c.png) , i.e.
, i.e.
![\begin{equation*}
|f(z_0) | - \Big| f \big( z_0 + r \exp(it) \big) \Big| = 0, \quad \forall t \in [0, 2 \pi]
\end{equation*}](../../assets/latex/complex_analysis_276a7754dcd149492473dfadbc8373a2f3ff4b01.png)
which is true for every point in  is of this form, for some
is of this form, for some  , and some
, and some ![$t \in [0, 2 \pi]$](../../assets/latex/complex_analysis_6dfb3baada6e4547107fe0697ceee11c7bf99f22.png) .
.
Hence  is constant on
is constant on  .
.
Let  , and
, and  be holomorphic and bounded on
be holomorphic and bounded on  , i.e.
, i.e.

for some  .
.
If  achives its maximum at
achives its maximum at  , then
, then  is constant on
is constant on  .
.
Series Expansions for Holomorphic Functions
Stuff
Let  be a power series.
be a power series.
Then 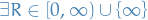 s.t.
s.t.
 converges if
converges if 
 converges uniformly on
converges uniformly on 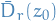 for all
for all 
 diverges if
diverges if 
 is holomorphic on its disc of convergence
is holomorphic on its disc of convergence 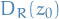 , where
, where  is the radius of convergence.
is the radius of convergence.
To proof holomorphicity of convergent power series, one could do as follows:
Fix  . Then
. Then  for some
for some  . Series converges uniformly on
. Series converges uniformly on 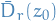 , thus partial sums are holomorphic, which implies series is holomorphic at
, thus partial sums are holomorphic, which implies series is holomorphic at  .
.
Let  be open, and
be open, and  .
.
Then we say that  is analytic if at everypoint
is analytic if at everypoint  ,
,  can be expressed as a convergent power series.
can be expressed as a convergent power series.
Suppose  is holomorphic on
is holomorphic on 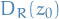 . Then the Taylor series
. Then the Taylor series
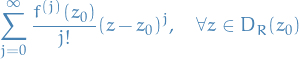
converges to  on
on 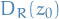 , and converges uniformly on
, and converges uniformly on  for all
for all 
where
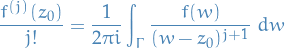
for any loop  with
with  .
.
It's REALLY important to realize that this Taylor series is only on some disk 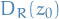 !!!
!!!
Therefore, if we know  is holomorphic on some open subset
is holomorphic on some open subset  , then if we want to talk about the Taylor series on any point
, then if we want to talk about the Taylor series on any point  , still can only say something about this on some disk
, still can only say something about this on some disk  !!
!!
The Taylor series at some point  is NOT necessarily the same as the Taylor series at some other point
is NOT necessarily the same as the Taylor series at some other point  .
.
Let  be the circle of radius
be the circle of radius  centered at
centered at  where
where 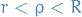 . By CIF we know that for
. By CIF we know that for 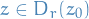 we have
we have
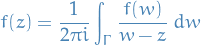
So
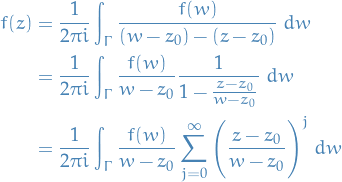
where we've used the fact that

thus
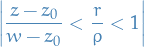
hence we could recognize the fraction above as the convergent series. Further, due to the series being convergent, we can interchange the summation and integration
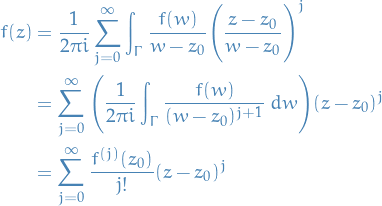
which is just the Taylor series!
Taylor series of a  (if it exists) is unique, i.e. if
(if it exists) is unique, i.e. if  is holomorphic on
is holomorphic on 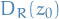 and
and

A anulus is


Suppose  is holomorphic on the anulus
is holomorphic on the anulus  .
.
Then

for any loop  with
with  for all
for all  , and the series converges uniformly on
, and the series converges uniformly on  for all
for all  .
.
We say  is a singularity if
is a singularity if  is not holomorphic at
is not holomorphic at  .
.
Suppose  has a singularity at
has a singularity at  .
.
If there exists  s.t.
s.t.  is holomorphic on the punctured disk
is holomorphic on the punctured disk  ,
,  has a Laurent series centred at
has a Laurent series centred at  , valid on this disk
, valid on this disk
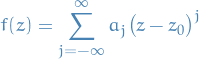
Then ONE of the following is true:
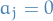 for all
for all  (
( is a removable singularity)
is a removable singularity) such that
such that  but
but 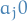 for all
for all  (
( is a pole of order
is a pole of order  )
) infinitively many negative
infinitively many negative  s.t.
s.t.  (
( is an essential singularity)
is an essential singularity)
If you have a removable singularity and then consider the integral along some loop around  .
.
Then the integral is the integral along some loop on which  is holomorphic, hence it's zero.
is holomorphic, hence it's zero.
We can therefore redefine  to take on the value
to take on the value  at the singularity point
at the singularity point  , and we got ourselves a holomorphic function on the non-punctured disk centered at
, and we got ourselves a holomorphic function on the non-punctured disk centered at  !
!
 is a zero of holomorphic function
is a zero of holomorphic function  if
if 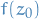 .
.
Further, we say it's a zero of order  if
if

but

Then
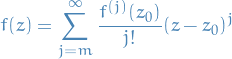
Let  ,
,  be a neighbourhood of
be a neighbourhood of  ,
,  be holomorphic on
be holomorphic on  , and such that
, and such that  for a sequence of distinct points
for a sequence of distinct points  which converge to
which converge to  .
.
Then  is identically zero on some disc centered at
is identically zero on some disc centered at  .
.
Let 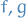 be holomorphic at
be holomorphic at  be a zero of
be a zero of 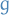 of order
of order  .
.
Then 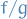 has
has
- has a pole of order
 at
at  if
if 
- has a pole of order
 (if
(if  ) at
) at  , if
, if  is a zero of order
is a zero of order  of
of  , OR
, OR  is a removable singularity if
is a removable singularity if 
Analytic continuation
Suppose  is holomorphic on a domain
is holomorphic on a domain  with
with  and
and  .
.
Then
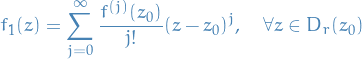
Power series above might have radius of convergence 
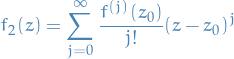
is a holomorphic on 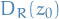 with
with  , i.e.
, i.e.

One might then as does  on
on  ?
?
Yes,  is an analytic continuation of
is an analytic continuation of  to
to  where
where
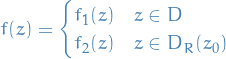
and  is well-defined.
is well-defined.
Let  be domain, and
be domain, and  be holomorphic.
be holomorphic.
We say that a holomorphic function 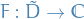 is an analytic continuation of
is an analytic continuation of  if
if

Let  be a domain,
be a domain,  , and
, and  be holomorpic on
be holomorpic on  and such that
and such that

for a sequence of distinct points  which converge to
which converge to  . Then
. Then

Let  be a domain,
be a domain,  , and
, and 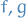 be holomorphic on
be holomorphic on  and such that
and such that

for a sequence of distinct points  which converge to
which converge to  . Then
. Then

Let 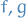 be holomorphic at
be holomorphic at  , where
, where  is zero of order
is zero of order  . Then
. Then
- if
 is not zero of
is not zero of  , then
, then 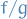 has a pole of order
has a pole of order  at
at 
- if
 is a zero of order
is a zero of order  of
of  , then
, then 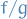 has a pole of order
has a pole of order  at
at  if
if  , and has a removable singularity at
, and has a removable singularity at  otherwise.
otherwise.
Cauchy Residue
Theorem
Let  ,
,  be holomorphic on the punctured disc
be holomorphic on the punctured disc  for some
for some  , with an isolated singularity at
, with an isolated singularity at  , and
, and  be a loop inside
be a loop inside  , with
, with  . Then
. Then
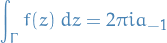
where  is the coefficient of the
is the coefficient of the  term in the Laurent expansion of
term in the Laurent expansion of  centred at
centred at  ,
,
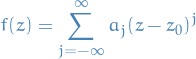
Let  and
and  be holomorphic on the punctured disc
be holomorphic on the punctured disc  , for some
, for some  , with an isolated singularity at
, with an isolated singularity at  .
.
Then the residue of  at
at  , is
, is

where  is the term in the Laurent series of
is the term in the Laurent series of  centered at
centered at  .
.
Let  , and
, and  be holomorphic on the punctured dist
be holomorphic on the punctured dist  for some
for some  , with removable singularity at
, with removable singularity at  . Then
. Then
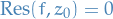
Let  and
and  be holomorphic on the punctured disc
be holomorphic on the punctured disc  , for some
, for some  , with a pole of order
, with a pole of order  at
at  . Then
. Then
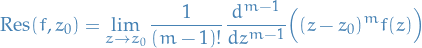
Let  and
and  ,
,  be holomorphic on
be holomorphic on  for some
for some  , such that
, such that  has a simple zero (
has a simple zero ( ) at
) at  , while
, while  . Then, defining
. Then, defining 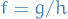 we have
we have
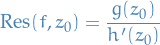
Let  be a loop, and
be a loop, and  be holomorphic inside and on
be holomorphic inside and on  except for finitely many isolated singularities
except for finitely many isolated singularities  . Then
. Then
Let  be a domain.
be a domain.
A function  is meromorphic on
is meromorphic on  if for all
if for all  , either
, either  has a pole at
has a pole at  or
or  is holomorphic at
is holomorphic at  .
.
Application: trigonometric integrals
Integrals of the form

for ration function  , can often be evaluated by considering a contour integral of appropriate function around the unit circle centered at
, can often be evaluated by considering a contour integral of appropriate function around the unit circle centered at  .
.
On  with
with  we have
we have
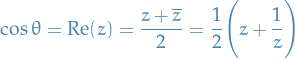
and
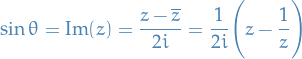
Defining  , we therefore have that
, we therefore have that

If  parametrized by
parametrized by ![$\gamma: [0, 2 \pi] \to \mathbb{C}$](../../assets/latex/complex_analysis_699254c6504a57def9b4a054d295d62330d9cb05.png) defined by
defined by  , then
, then

It basically comes down to rewriting  and
and  with
with  , which then often provides us with a rational function of which it's substantially esaier to obtain the singularities, thus the residue, hence the integral around
, which then often provides us with a rational function of which it's substantially esaier to obtain the singularities, thus the residue, hence the integral around  .
.
Improper Integrals
We define the Cauchy principal value of the integral
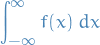
as
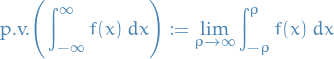
Let 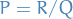 be a rational function, where
be a rational function, where
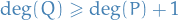
ad  such that
such that  . Then
. Then
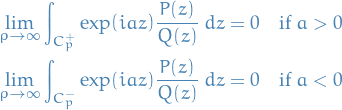
where  and
and  are the semicircular contours from
are the semicircular contours from  to
to  in the upper and lower half-plane, respectively.
in the upper and lower half-plane, respectively.
Let
 be a domain
be a domain ,
,  be meromorphic on
be meromorphic on  with a simple pole at
with a simple pole at 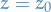
 be the circular arc parametrized by
be the circular arc parametrized by  for
for ![$\theta \in [\theta_0, \theta_1]$](../../assets/latex/complex_analysis_ba56d81b64220ba9ec70aed503bbe930a6deefd6.png) for some
for some  .
.
Then
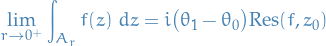
Let  , and let
, and let  be a loop with
be a loop with  . Then
. Then
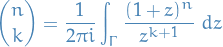



 be holomorphic and such that
be holomorphic and such that

 for all
for all