Conditional Random Fields (CRFs)
Table of Contents
Overview
- Graphical model
- Is a discriminative model => attempts to directly model

Graphical models
Distributions over very many variables can often be represented as a product of local functions that depend on a much smaller subset of variables.
Undirected models
Notation
 is a set of rvs. that we target
is a set of rvs. that we target takes outcomes from the (continuous or discrete) set
takes outcomes from the (continuous or discrete) set 
 is an arbitrary assignment to
is an arbitrary assignment to 
 denotes value assigned to
denotes value assigned to 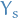 by
by 
 is summation over all possible combinations of
is summation over all possible combinations of  where
where 
 is factor where
is factor where  is an index in
is an index in  ,
, 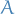 being the number of factors
being the number of factors is a indicator variable, having value
is a indicator variable, having value  if
if  and
and  otherwise
otherwise for some rvs.
for some rvs.  denotes the neighbors of
denotes the neighbors of  in some graph
in some graph 
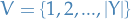 usually denotes indices for rvs. of some graph
usually denotes indices for rvs. of some graph 
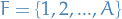 usually denotes the indices for factors of some graph
usually denotes the indices for factors of some graph 
Factors
- Believe probability distribution
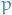 can be represented as a product of
factors
can be represented as a product of
factors 
- Each factor
 depends only on a subset
depends only on a subset  of the variables
of the variables - Non-negative scalar which can be thought of a compatibility measure between
the values
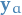
Formally, given a collections of subs  of
of  , an unidirected graphical model
is the set of all distributions that can be written as
, an unidirected graphical model
is the set of all distributions that can be written as
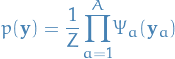 1
1
for any choice of factors  that have
that have 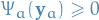 for all
for all 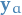 .
.
We use the term random field to refer to a particular distribution among those defined by a unidirected graphical model.
The constant  is the normalization factor (also referred to as the
parition function) that ensures the distribution
is the normalization factor (also referred to as the
parition function) that ensures the distribution 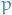 sums to
sums to  .
.
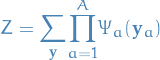 2
2
Notice that the summation in  is over the exponentially many possible assignments
is over the exponentially many possible assignments  .
.
Factor graph
A factor graph is biparite graph 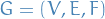 , i.e. a graph with
two disjoint sets of nodes
, i.e. a graph with
two disjoint sets of nodes  and
and  :
:
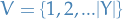 indexes the rvs. in the model
indexes the rvs. in the model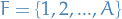 indexes the factors
indexes the factors
By this representation, we mean that if a variable node 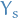 for
for  is connected to a
factor node
is connected to a
factor node  for
for  then
then 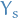 is one of the arguments of
is one of the arguments of  .
.
Markov network
A Markov network represents the conditional independence relationships
in a multivariate distribution, and is a graph over random variables only.
That is;  is a graph over integers (rv. indices)
is a graph over integers (rv. indices)  .
.
A distribution 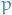 is Markov with respect to
is Markov with respect to  if it satisfies the local
Markov property: for any two variables
if it satisfies the local
Markov property: for any two variables  , the variable
, the variable 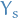 is independent of
is independent of 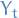 conditioned on its neighbors,
conditioned on its neighbors,  . Intuitively,
this means that
. Intuitively,
this means that  contains all the information that is useful for
predicting
contains all the information that is useful for
predicting 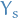
An issue with a Markov network is that it is ambigious, i.e. "not descriptive enough" from the factorization persepective. If you have a look at the figure below you can see an example of what we're talking about.
Any distribution that factorizes as  for some
positive function
for some
positive function  is Markov with respect to this graph. However, we
might want to represent the graph using a more restricted parameterization,
where
is Markov with respect to this graph. However, we
might want to represent the graph using a more restricted parameterization,
where 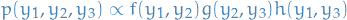 . This is a more strict
family of functions, and so one would expect it to be easier to estimate.
Unfortunately, as we can see in the figure, Markov networks doesn't really
distinguish between these cases. Lucky us, factor graphs do!
. This is a more strict
family of functions, and so one would expect it to be easier to estimate.
Unfortunately, as we can see in the figure, Markov networks doesn't really
distinguish between these cases. Lucky us, factor graphs do!
Directed Models
- Describes how the distribution factorizes into a local conditional probability distribution.
Inference
Belief propagation
Notation
 is the variable we want to compute the marginal distribution for
is the variable we want to compute the marginal distribution for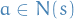 is the neighborhood of *factors of
is the neighborhood of *factors of  , and it's the index of the neighboring factor of
, and it's the index of the neighboring factor of 
 the set of variables "upstream" of
the set of variables "upstream" of  , i.e. set of variables
, i.e. set of variables  for which the factor
for which the factor  is between
is between  and
and  (
( separates
separates  and
and  ), with
), with  being the index of a neighboring factor of
being the index of a neighboring factor of 
 the set of factors "upstream" of
the set of factors "upstream" of  , i.e. set of factors for which
, i.e. set of factors for which  is between those and
is between those and  ("separates"
("separates"  from this set of factors), including the factor
from this set of factors), including the factor  itself
itselfMessage from
 to
to 

Stuff
- Direct generalization of exact algorithms for Linear CRFs (i.e. Viterbi algorithm for sequences and Forward-backward algorithm for joint distributions)
- Each neighboring factor of
 makes a multiplicative contribution to the marginal of
makes a multiplicative contribution to the marginal of  , called a message
, called a message
In the special case where our graph is a tree, the graph itself is a the one and only spanning tree, hence we partition the entire graph wrt.  : the sets
: the sets  form a partition of the variables in
form a partition of the variables in  . In a bit simpler wording:
. In a bit simpler wording:
- You're looking at

- Choose some other variable (node in the graph)

- All variables between
 and
and  are along a single path (i.e. only one possible way to traverse from
are along a single path (i.e. only one possible way to traverse from  to
to  )
) - Therefore, the sets
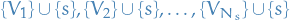 form a partition of the variables in
form a partition of the variables in  , where
, where  denotes the number of neighboring nodes of
denotes the number of neighboring nodes of 
- Thus, we can split upt the summation required for the marginal into a product of independent subproblems
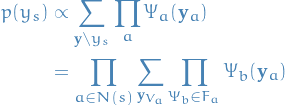
And denoting each of the factors in the above equation by  , i.e.,
, i.e.,

which can be though of as a message from  to
to  .
.
And also, if instead take the product over neighboring factors, we can define the message from variables to factors as

which would give us

Let's break this down:
 is product over all variables
is product over all variables  which are neighbors to the factor
which are neighbors to the factor 
 are all possible values the variables
are all possible values the variables  (i.e. "variables on one side of
(i.e. "variables on one side of  , including
, including  ") can take on
") can take on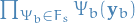 is the product over all neigboring factors
is the product over all neigboring factors  of the variable
of the variable  , excluding
, excluding  itself (which is our "focus" at the moment)
itself (which is our "focus" at the moment)
Observe that when talking about the "marginal for a factor ", we're looking at the marginal of a vector 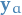 rather than a single value
rather than a single value  as in the marginal for a variable.
as in the marginal for a variable.
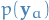 denotes the vector of random variables
denotes the vector of random variables  with
with  which are incoming to
which are incoming to  , NOT the distribution over the output of
, NOT the distribution over the output of 
Luckily, we can rewrite the messages recursively
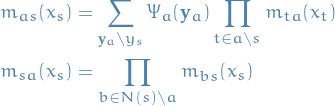
These recursion-relations define the belief propagation algorithm.
Belief progagation is the algorithm defined by the following recursion relations:
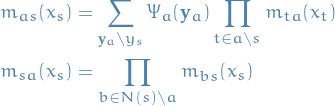
In the case where the graph  is not a tree, we do not have the guarantee of convergence and refer to this algorithm as loopy belief propagation, as we can still find a fixed point.
is not a tree, we do not have the guarantee of convergence and refer to this algorithm as loopy belief propagation, as we can still find a fixed point.
As it turns out, Loopy BP can in fact be seen as a variational method, meaning that there actually exists an objective function over beliefs that is approximately minimized by the iterative BP procedure.
Appendix A: Vocabular
- random field
- a particular distribution among those defined by an unidirected graphical model
- biparite graph
- set of graph vertices decomposed into two disjoint sets s.t. no two graph vertices from the same set are adjacent / "directly connected".
- markov blanket
- simply a fancy word for the independent neighbors
- multivariate distribution
- distribution of multiple variables
Appendix B: Discriminative vs. Generative methods
- Discriminative model
- attempts to model
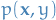 , and thus indirectly model
, and thus indirectly model  using Bayes'
using Bayes' - Generative model
- attemps to model
 directly
directly
First, it's very hard (impossible?) to tell beforehand whether a generative or discriminative model will perform better on a given dataset. Nonetheless, there are some benefits/negatives to both.
Benefits of discriminative:
- Agnostic about the form of

- Make independence assumptions among
 and how
and how  depend on
depend on  , but
do not make conditional independence assumptions between the $$s
, but
do not make conditional independence assumptions between the $$s - Thus, these models are better at suited for including rich, overlapping (dependent) features.
- Better probability estimates than generative models; consider a vector of features
 which we transform to repeat the features, like so
which we transform to repeat the features, like so 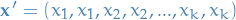 .
Then train, say a Naive Bayes', on this data. Even though no new data has been added
(just added multiple completely correlated features), the model will be more confident
in the probability estimates, i.e.
.
Then train, say a Naive Bayes', on this data. Even though no new data has been added
(just added multiple completely correlated features), the model will be more confident
in the probability estimates, i.e.  will be further away from
will be further away from  than
than  .
Note that his in a way demonstrates the independence assumption between the features which
is beeing made a generative model.
.
Note that his in a way demonstrates the independence assumption between the features which
is beeing made a generative model.
Benefits of generative model:
- More natural for handling latent variables, partially-labeled data, and unlabeled data. Even in extreme case of unlabeled data, generative models can be applied, while discriminative methods is less natural.
- In some cases, generative model can perform better, intuitively because
 might have a smoothening effect on the conditional.
might have a smoothening effect on the conditional. - If application of the model requires both prediction of future inputs as well as outputs, generative models is a good choice since they model the joint distribution, and so we can potentially marginalize over whatever we don't want to predict to obtain a prediction for our target variable (being input or output).
It may not be clear why these approaches are different, as you could convert from one to the other, both ways, using Bayes' rule.
TODO Ongoing work
One interesting way to look at it is as follows:
Suppose we have a generative model  which takes the form:
which takes the form:
 3
3
And using the chain rule of probability we get
 4
4
where:
 is computed by inference
is computed by inference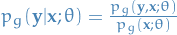 is computed by inference
is computed by inference
And then suppose we another model, but this is discriminative model  :
:
Resources
Named Entity Recognition with a Maximum Entropy Approach A paper using MEMMs for word-tagging. I link this here since MEMMs are very similar to CRFs, but also because they provide a very nice set of features for use in word-tagging, which is something you might want to use CRFs for.
In fact, both CRFs and MEMMs are discriminative, unlike the generative HMMs, sequence models. Both CRFs and MEMMs are MaxEnt (maximum entropy) models, but a CRF is models the entire sequence while MEMMs makes decisions for each state independently of the other states.
