Numerical Differential Equations
Table of Contents
Notation
 almost always referes to the Lipschitz constant
almost always referes to the Lipschitz constant refers to LHS of a first-order system
refers to LHS of a first-order system denotes a "sampled" value of
denotes a "sampled" value of  at
at  , using our approximation to
, using our approximation to 
 refers to a flow-map, with
refers to a flow-map, with  assuming
assuming 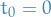 (as we can always do)
(as we can always do) refers to the discrete approx. of the flow-map
refers to the discrete approx. of the flow-map refers to the spatial domain, i.e.
refers to the spatial domain, i.e.  for some
for some 
 denote the space of real polynomials of degree
denote the space of real polynomials of degree 
 denotes the i-th abscissa point
denotes the i-th abscissa point
Definitions
Continuous mechanics
A system of differential equations for which  can be written as a function of
can be written as a function of 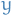 only is an autonomous-differential-equation (often referred to as continuous mechanics):
only is an autonomous-differential-equation (often referred to as continuous mechanics):
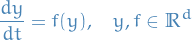
Euler's method
We start by taking the Taylor expansion of the solution  of the system:
of the system:
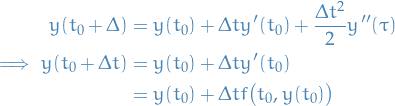
for some ![$\tau \in [t_0, t_0 + \Delta t]$](../../assets/latex/numerical_differential_equations_ae24eff094cbb8854060e5bf67945dc899a4d3e4.png) .
.
We have the ODE
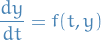
and the steps are defined as

for
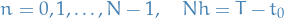
where  denotes our approximation for
denotes our approximation for  .
.
What we're doing in Euler's method is taking the linear approximation to  at each point
at each point  , but in an interative manner, using our approximation for
, but in an interative manner, using our approximation for  , at the previous step
, at the previous step  to evaluate the point
to evaluate the point  .
.
This is because we can evaluate  , since
, since  but we of course DON'T know
but we of course DON'T know  .
.
y = @(t, y0) (y0 * exp(t) ./ (1 - y0 + y0*exp(t)) y0 = 0.2; T=0:0.5:5; plot(T, y(T, t0));
Butcher table
Flow map
Consider the IVP:
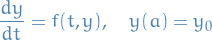
which is assumed to have a unique solution on ![$[a, b]$](../../assets/latex/numerical_differential_equations_c9a1e8df376ecb942b106e02d3e6d1b417da2600.png) .
.
The flow map  is then an approximation to a specific solution (a trajectory), i.e. starting at some
is then an approximation to a specific solution (a trajectory), i.e. starting at some  such that
such that 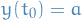 and
and  , which we write
, which we write

Observe that it's NOT a discrete approximation, but is continuous.
Adjoint sensitivity analysis
The (local) sensitivity of the solution ot a parameter is defined by how much the solution would change by changes in the parameter, i.e. the sensitivity of the i-th independent variable to the j-th parameter is  .
.
Sensitivity analysis serves two major purposes:
- Diagnostics useful to understand how the solution will change wrt. parameters
- Provides a cheap way to compute the gradient of the solution which can be used in parameter estimation and other optimization tasks
Theorems
Lipschitz convergence
Suppose a given sequence of nonnegative numbers satisfies

where  are nonnegative numbers
are nonnegative numbers  , then, for
, then, for 
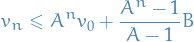
Local Existence / Uniqueness of Solutions
Suppose  is:
is:
- continuous
- has continuous partial derivatives wrt. all components of the dependent variable
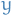 in a neighborhood of the point
in a neighborhood of the point 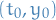
Then there is an interval  and unique function
and unique function 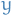 which is continuously differentiable on
which is continuously differentiable on  s.t. it satisfies
s.t. it satisfies

Methods
Euler method
Trapezoidal rule
The Trapezoidal rule computes the average change on the interval ![$[t_n, t_{n + 1}]$](../../assets/latex/numerical_differential_equations_b2f5e1b2fca31fe3098567af2832a78ff743a609.png) , allowing more accurate approximation to the integral, and the update rule is defined as follows:
, allowing more accurate approximation to the integral, and the update rule is defined as follows:
![\begin{equation*}
y_{n + 1} = y_n = \frac{h}{2} \Big[ f(t_n, y_n) + f(t_{n + 1}, y_{n + 1}) \Big]
\end{equation*}](../../assets/latex/numerical_differential_equations_86e7fc1fa54c80bb530ae0f1d26b9740eaade151.png)
Heun-2 (implicit approx. to Trapezoidal rule)
The Heun-2 update rule is an implicit approximation to Trapezoidal rule, where we've replaced the explicit computation of the endpoint 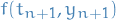 which depend on
which depend on  , with a function of the current estimate
, with a function of the current estimate  :
:
![\begin{equation*}
y_{n + 1} = y_n + \frac{h}{2} \Big[ f(t_n, y_n) + f \big(t_n + h, y_n + h f(t_n, y_n) \big) \Big]
\end{equation*}](../../assets/latex/numerical_differential_equations_23e6b5add77d8f8d2c4570510ffdfecea7620a8a.png)
Convergence of one-step methods
Notation
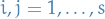


 denotes the stage values, s.t.
denotes the stage values, s.t. 
Approximation
In this chapter we focus on the autonomous differential equation

but the non-autonomous differential equation

can be treated using similar methods.
The global error after  time steps is the difference between the discrete approx. and the exact solution, i.e.
time steps is the difference between the discrete approx. and the exact solution, i.e.

A method is said to be convergent if, for every  ,
,
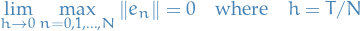
We have the Taylor expansion given by

for some "perturbation"  about
about  .
.
For a scalar function, assuming  is
is  times continuously differentiable (i.e.
times continuously differentiable (i.e.  ), Taylor's theorem states that
), Taylor's theorem states that
![\begin{equation*}
\exists t^* \in [t, t + \tau] : \quad y(t + \tau) = \sum_{i=0}^{\nu - 1} \frac{\tau^i}{i!} \frac{d^i y}{dt^i}(t) + \frac{\tau^\nu}{\nu!} \frac{d^\nu}{dt^\nu} (t^*)
\end{equation*}](../../assets/latex/numerical_differential_equations_fead1aae8c45680e1420768ad459bcf1a912c05e.png)
Thus, the norm of the last (remainder) term is bounded on ![$[t, t + \tau]$](../../assets/latex/numerical_differential_equations_a78a6ed4d0eb893d00aa7864a018518e735aae50.png) , and we have
, and we have

for some constant  , and thus we write
, and thus we write
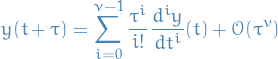
in general.
For a vector function ( ), Taylor's theorem still holds componentwise, but in general the mean value will be attained at a different
), Taylor's theorem still holds componentwise, but in general the mean value will be attained at a different  for each component.
for each component.
Local error of a numerical method is the difference between the (continuous) flow-map  and its (discrete) approx.
and its (discrete) approx.  :
:

Which measures how much error is introduced in a single timestep of size  .
.
A method is said to be consistent if and only if the local error satisfies

where  is a constant that depends on
is a constant that depends on  and its derivatives, and
and its derivatives, and  .
.
A method is said to be stable if and only if it satisfies an h-dependent Lipschits condition on  (the spatial domain)
(the spatial domain)
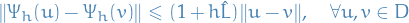
where  is not necessarily the Lipschitz constant for the vector field.
is not necessarily the Lipschitz constant for the vector field.
Given a differential equation and a generalized one-step method  which is consistent and stable, the global error satisfies
which is consistent and stable, the global error satisfies

Let the error be

so
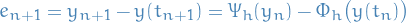
Then, adding and subtracting by  ,
,
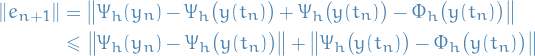
Then, using the fact that the method is consistent and stable, we write

Using this theorem, yields
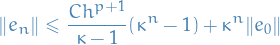
where 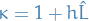 . Finally, since
. Finally, since 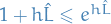 and therefore
and therefore  , if we assume the initial condition is exact (
, if we assume the initial condition is exact (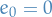 ), we get the uniform bound
), we get the uniform bound
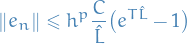
which proves convergence at order 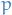 .
.
A really good way of estimating the order of convergence 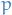 for the maximum global error wrt.
for the maximum global error wrt.  , is to plot
, is to plot  vs.
vs.  on a log-log plot since
on a log-log plot since

Thus, 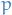 is the slope of
is the slope of 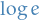 .
.
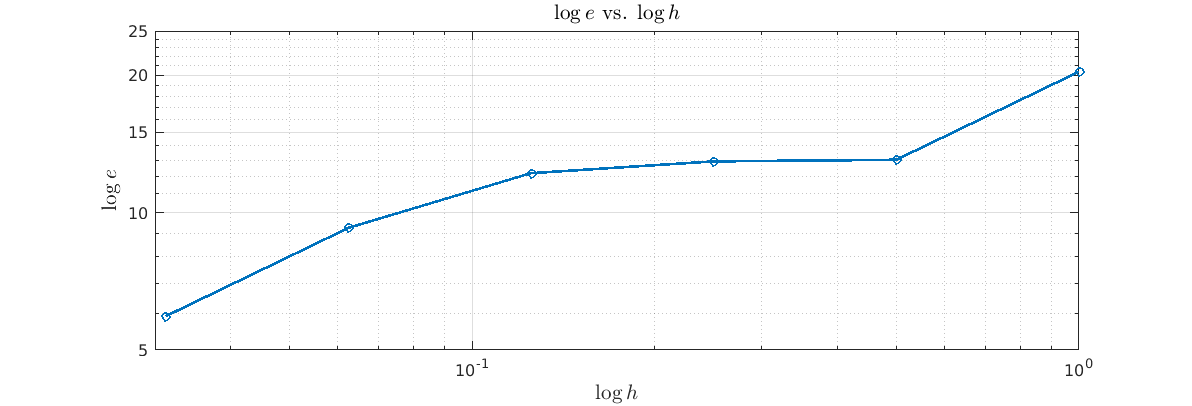
Figure 1: Observe that for smaller values of  we have
we have 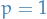 , i.e.
, i.e.  decreases wrt.
decreases wrt.  , while for larger values of
, while for larger values of  we have
we have  , i.e. decrease in
, i.e. decrease in  is not even on the order of 1.
is not even on the order of 1.
Consider a compact domain  and suppose
and suppose  is a smooth vector field on
is a smooth vector field on  and has a Lipschitz constant
and has a Lipschitz constant  on
on  (since
(since  is smooth, we can take
is smooth, we can take  ).
).
Then, since
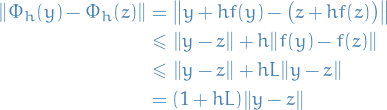
the numerical flow map is Lipschitz with  .
.
The exact solution satisfies

Therefore the local error is
![\begin{equation*}
le(y, h) = y + h f(y) - \Bigg[ y + hf(y) + \frac{h^2}{2} \frac{d^2 y }{dt^2} + \mathcal{O}(h^3) \Bigg] = \mathcal{O}(h^2)
\end{equation*}](../../assets/latex/numerical_differential_equations_3410bed7647f829cf8d930f9adbc7da20d3aefc4.png)
and we can apply the convergence theorem for one-step methods with  to show that Euler's method is convergent with order
to show that Euler's method is convergent with order 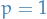 .
.
Construction of more general one-step methods
Usually one aims to approximate the integral between two steps:
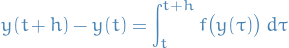
A numerical method to approximate a definite integral of one independent variable is known as numerical quadrature rule.
Example: Trapezoidal rule
The approximation rule becomes:
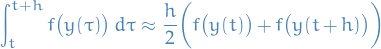
which results in the trapezoidal rule numerical method:

This is an implicit method, since we need to solve for  to obtain the step.
to obtain the step.
Polynomial interpolation
Given a set of abscissa points  and the corresponding data
and the corresponding data  , there exists a unique polynomial
, there exists a unique polynomial  satisfying
satisfying

called the interpolating polynomial.
The Lagrange interpolating polynomials 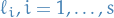 for a set of abscissae are defined by
for a set of abscissae are defined by
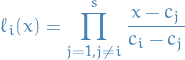
Observe that 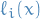 then has the property
then has the property
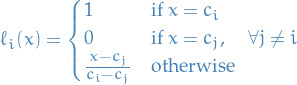
Thus, the set of Lagrange interpolating polynomials form a basis for  . In this basis, the interpolating polynomial
. In this basis, the interpolating polynomial  assumes the simple form
assumes the simple form
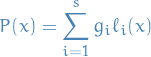
We also know from Stone-Weierstrass Theorem that the polynomials are dense in 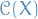 for some compact metric space
for some compact metric space  (e.g.
(e.g.  ).
).
Also, if it's not 100% clear why 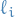 form a basis, simply observe that if
form a basis, simply observe that if 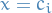 then
then
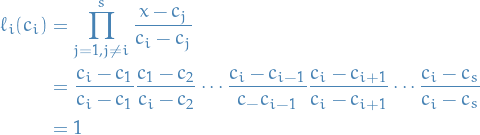
and if  , then we'll multiply by a factor of
, then we'll multiply by a factor of  , hence
, hence

as wanted. Thus we have  lin. indep. elements, i.e. a basis.
lin. indep. elements, i.e. a basis.
Numerical quadrature
We approximate the definite integral of 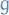 based on the interval
based on the interval ![$[0, 1]$](../../assets/latex/numerical_differential_equations_68c8fa38d960e53d4308cbf1e65d04c66a554817.png) by exactly integrating the interpolating polynomial of order
by exactly integrating the interpolating polynomial of order  based on
based on  points
points  .
.
The points  are known as quadrature points.
are known as quadrature points.
We make the following observation:
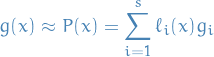
We're interested in approximating the integral of  on the interval
on the interval ![$[t_0, t_0 + h]$](../../assets/latex/numerical_differential_equations_f38efebf139d789519aaac8538255ff29e6b6e1d.png) , thus
, thus
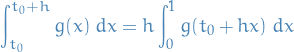
using the change of variables  . With the polynomial approx. we then get
. With the polynomial approx. we then get
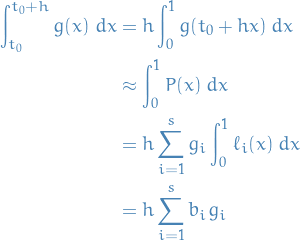
where we've let
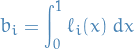
The integral-approximation above is called a quadrature formula.
By construction, a quadrature formula using  distinct abscissa points will exactly integrate any polynomial in
distinct abscissa points will exactly integrate any polynomial in  (remember that
(remember that  are integrals).
are integrals).
We can do better; we say that quadrature rule has order 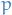 if it exactly integrates any polynomial
if it exactly integrates any polynomial  . It can be shown that
. It can be shown that  always hold, and, for optimal choice of
always hold, and, for optimal choice of  , we have
, we have 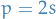 .
.
That is, if we want to exactly integrate some polynomial of order 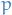 , then we only need half as many quadrature points
, then we only need half as many quadrature points  !
!
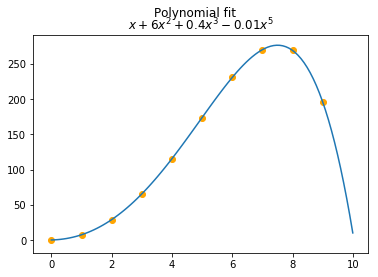
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
x = np.arange(10)
y = x + 6 * x ** 2 + 0.4 * x ** 3 - 0.01 * x ** 5
def polynomial_fit(abscissae, y):
s = abscissae.shape[0]
zeros = np.zeros((s, s - 1))
for i in range(s):
if i == 0:
zeros[i] = x[i + 1:]
elif i == s - 1:
zeros[i] = x[:i]
else:
zeros[i] = np.hstack((x[:i], x[i + 1:]))
denominators = np.prod(abscissae.reshape(-1, 1) - zeros, axis=1) ** (-1)
def p(x):
return np.dot(np.prod(x - zeros, axis=1) * denominators, y)
return p
p = polynomial_fit(x, y)
xs = np.linspace(0, 10, 100)
ys = [p(xs[i]) for i in range(xs.shape[0])]
plt.plot(xs, ys)
plt.suptitle("Polynomial fit")
plt.title("$x + 6x^2 + 0.4x^3 - 0.01x^5$")
_ = plt.scatter(x, y, c="orange")
One-step collocation methods
Let  be the collocation polynomial of degree
be the collocation polynomial of degree  , satisfying
, satisfying
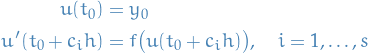
Then we attempt to approximate the gradient as a polynomial, letting 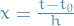 :
:
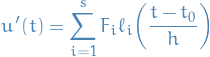
where we've let
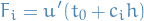
Then by the Fundamental Theorem of Calculus, and making the substitution 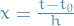 :
:
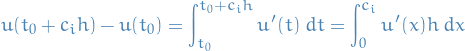
And, using our Lagrange polynomial approximation:
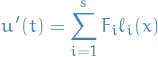
we get
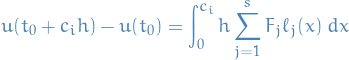
Aaand finally, 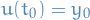 as stated earlier, hence
as stated earlier, hence
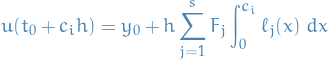
for all  . And since
. And since  , we get
, we get
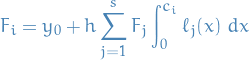
which gives us a system of (non-linear) equations we need to solve simultaneously.
And therefore, our next step 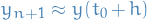 is given by
is given by
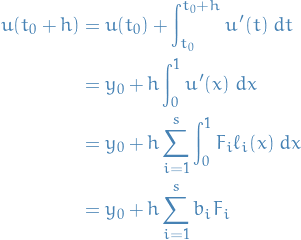
where we've let
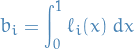
Thus,
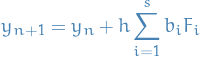
Let  be the collocation polynomial of degree
be the collocation polynomial of degree  , satisfying
, satisfying
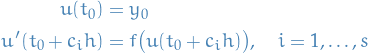
and let  be the values of the (as of yet undetermined) interpolating polynomial at the nodes:
be the values of the (as of yet undetermined) interpolating polynomial at the nodes:

Then we attempt to approximate the gradient as a polynomial, letting 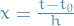 :
:
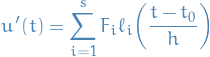
The following is something I was not quite getting to grips with, at first.
Now we make the following observation:
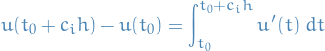
by the Fundamental Theorem of Calculus. Thus, making the substitution 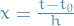 , gives
, gives
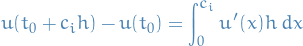
And, using our Lagrange polynomial approximation:
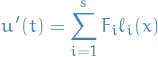
we get
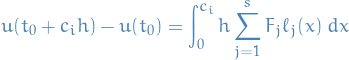
Aaand finally, 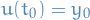 as stated earlier, hence
as stated earlier, hence
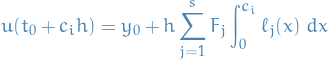
for all  .
.
Let us denote
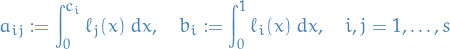
Then, a collocation method is given by
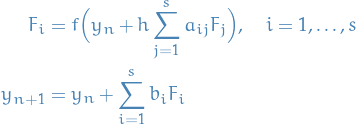
where one first solves the coupled sd-dimensional nonlinear system  , and the update
, and the update  explicitly.
explicitly.
Important: here we're considering  , rather than the standard
, rather than the standard  , but you can do exactly the same but by plugging in
, but you can do exactly the same but by plugging in  in the condition for
in the condition for  instead of what we just did.
instead of what we just did.
Comparing to interpolating polynomial,  becomes the
becomes the  sort of.
sort of.
Using the collocation methods we obtain a piecewise continuous solution, or rather, a continuous approximation of the solution  on each interval
on each interval ![$[t_n, t_{n + 1}]$](../../assets/latex/numerical_differential_equations_b2f5e1b2fca31fe3098567af2832a78ff743a609.png) .
.
In terms of order of accuracy, the optimal choice is attained by using so-called Guass-Legendre collocation methods and placement of nodes at the roots of a shifted Legendre polynomial.
Runge-Kutta Methods
A natural generalization of collocation methods is obtained by:
- allow coefficients
 ,
,  and
and  to take on arbitrary values (not necessarily related to the quadrature rules)
to take on arbitrary values (not necessarily related to the quadrature rules) - no longer assume
 to be distinct
to be distinct
We then get the class of Runge-Kutta methods!
We introduce the stage values 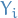 , ending up with what's called the Runge-Kutta methods:
, ending up with what's called the Runge-Kutta methods:
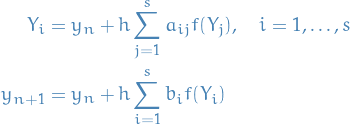
where we can view 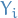 as the intermediate values of the solution at
as the intermediate values of the solution at 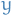 at time
at time  .
.
For which we use the following terminology:
 the number of stages of the Runge-Kutta method
the number of stages of the Runge-Kutta method are the weights
are the weights are the internal coefficients
are the internal coefficients
Euler's method and trapezoidal rule are Runge-Kutta methods, where

gives us the Euler's method.
If the matrix  is strictly lower-triangular, then the method is explicit.
is strictly lower-triangular, then the method is explicit.
Otherwise, the method is implicit, as the we might have "circular" dependency between two stages 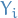 and
and 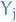 ,
,  .
.
Examples of Runge-Kutta methods
Runge-Kutta method with 4 stages - "THE Runge-Kutta method"
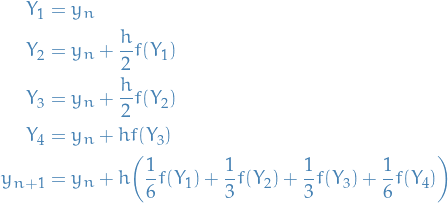
Which often are represented schematically in a Butcher table.
Accuracy of Runge-Kutta methods
Notation
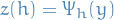 is the discrete approximation to the flow map, treating
is the discrete approximation to the flow map, treating 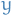 as constant
as constantIn the case of RK method, we write
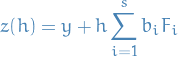
where
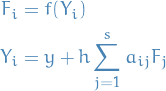
then
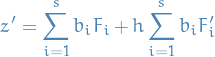
Stuff
- In general, we cannot have an exact expression for the local error

- Can approximate this by computing Taylor expansion wrt.

Consider the case of continuous mechanics, the derivates can be related directly to the solution itself by using the differential equation:
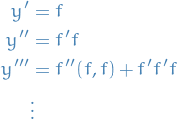
Then, we can write the flow map as
![\begin{equation*}
\Phi_h(y) = y + hf + \frac{h^2}{2} f' f + \frac{h^3}{6} [f''(f, f) + f' ff] + \mathcal{O}(h^4)
\end{equation*}](../../assets/latex/numerical_differential_equations_bf9f7b7fc017af87b37a0cc7ed6b033cfab6dff2.png)
Order conditions for Runge-Kutta methods
With
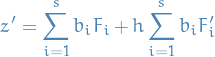
we have
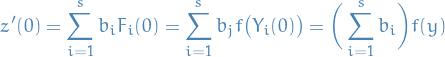
For the method to have order of 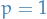 , we must have
, we must have
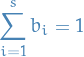
since we will then have

and thus, the method will be of order 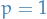 . This is the first what is termed as order conditions.
. This is the first what is termed as order conditions.
Then, to get the second order condition, we simply compute the second order derivative of  :
:
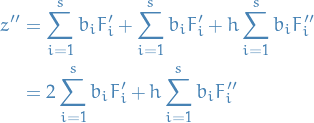
Substituting in the expressions for  and
and 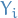 , we obtain
, we obtain
Variable stepsize
Notation
 and
and  are two different methods for numerical approximations to the flow map
are two different methods for numerical approximations to the flow map is order
is order 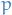 (local error
(local error 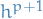 )
) is order
is order  (local error
(local error 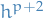 )
)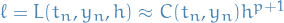
Stuff
Difference in an estimate of the local error by two different methods

And we assume the local error satisfies

i.e. that 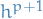 is the dominating factor.
is the dominating factor.
Error control
Assumptions:
 is a convergent one-step method
is a convergent one-step method- Desire local error at each step less than a given

 estimates the local error at a given point
estimates the local error at a given point 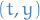 when we take a step size of
when we take a step size of 
Idea:
- Estimate the local error with

- If
 then decrease
then decrease  and redo step
and redo step - If
 then keep step; may want to increase
then keep step; may want to increase 
Question: how much do we decrease / increase  ?
?
Suggestion: raise/lower timestep by a factor 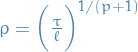
Can be inefficient in the case where we need to do this guessing multiple times, can instead do:

for some
![$\gamma \in [0, 1]$](../../assets/latex/numerical_differential_equations_a22fe950ebf3e28876d24d5ff9e5a489198e88b8.png) , e.g.
, e.g.  , i.e.
, i.e.  is a decaying factor for the "guess" of the stepsize.
is a decaying factor for the "guess" of the stepsize.
Stability of Runge-Kutta Methods
Notation
Stuff
An equilibrium point  of the scalar differential equation
of the scalar differential equation
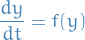
is a point for which
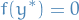
Fixed points which are NOT equilibrium points are called extraneous fixed points.
These are points such that

Stability of Equilibrium points
Suppose that  in
in
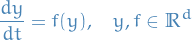
is  , i.e.
, i.e.  , and has equilibrium point
, and has equilibrium point  .
.
If the eigenvalues of

all lie strictly in the left complex half-plane, then the equilibrium point  is asymptotically stable.
is asymptotically stable.
If 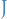 has any eigenvalue in the right complex half-plane, then
has any eigenvalue in the right complex half-plane, then  is an unstable point.
is an unstable point.
Stability of Fixed points of maps
We say a numerical method is A-stable if the stability region includes the entire left half-plane, i.e.  is a contained in the stability region.
is a contained in the stability region.
A A-stable numerical method has the property that it's stable at the origin.
I was wondering why  ? I believe it's because we're looking at solutions which are exponential, i.e.
? I believe it's because we're looking at solutions which are exponential, i.e.  , hence if
, hence if  , then the exponential will have modulus smaller than 1:
, then the exponential will have modulus smaller than 1:

if  , for
, for  .
.
We say a numerical method is L-stable if it has the properties:
- it's A-stable
 as
as 
Stability of Numerical Methods
Stability functions
- Scalar case
Consider
 , thus Euler's method has the form
, thus Euler's method has the form

where

Consider the scalar first-order diff. eqn

When applied to this diff. eqn., many methods, including all explicit Runge-Kutta methods, have the form

for some polynomial
 .
.
More generally, all RK methods have the form
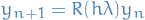
where
 is rational polynomial, i.e.
is rational polynomial, i.e.
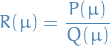
Then we call
 the stability function of the RK method.
the stability function of the RK method.
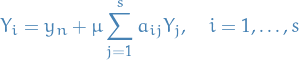
 , then we can write this sum in a matrix form:
, then we can write this sum in a matrix form:

which has the solution
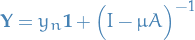
and therefore, finally, we can write
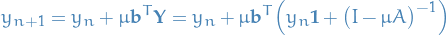

which gives us the stability function
 for RK:
for RK:
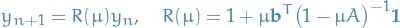
Stability of Numerical Methods: Linear case
Linear system of ODEs

where  is diagonalisable. Can write solution as
is diagonalisable. Can write solution as


where  is a diagonalisable matrix.
is a diagonalisable matrix.
Further, let an RK method be given with stability function  . The origin is stable for numerical method is stable if and only if
. The origin is stable for numerical method is stable if and only if

Linear Multistep Methods
Notation

 where
where 
Definitions
A linear k-step method is defined as
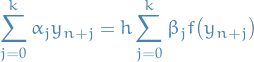
where  and either
and either  or
or  .
.
The coefficients are usually normalized such that either

In implementation is's assumed that the values  are already computed, so that
are already computed, so that  is the only unknown in the formula.
is the only unknown in the formula.
If  is non-zero the method is implicit, otherwise it's explicit.
is non-zero the method is implicit, otherwise it's explicit.
Examples
 method - generalization of one-step methods
method - generalization of one-step methods
The  multistep method is of the form
multistep method is of the form
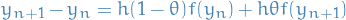
which is a linear k-step method with coefficients  ,
, 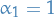 ,
, 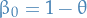 and
and 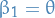 .
.
Examples:
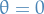 gives the Forward Euler
gives the Forward Euler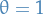 gives the Backwards Euler
gives the Backwards Euler gives the Trapezoidal rule
gives the Trapezoidal rule
Leapfrog
Adams methods
The class of Adams methods have
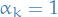

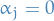 for
for 
If we also have the additional 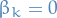 , we have explicit Adams methods, known as Adams-Bashforth methods, e.g.
, we have explicit Adams methods, known as Adams-Bashforth methods, e.g.
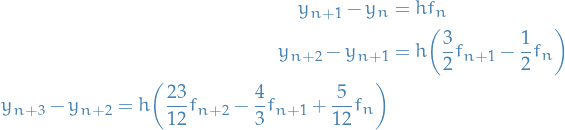
where 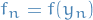 .
.
Adams-Moulton methods are implicit, i.e.  .
.
Backward differentiation formulae (BDF)
The Backward differentiation formulae (BDF) are a class of linear multistep methods satisfying
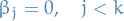
and generalizing backward Euler.
E.g. the two-step method (BDF-2) is
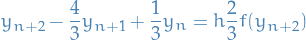
Order of accuracy
Associated with the linear multistep method are the polynomials
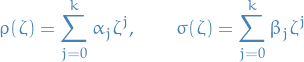
Let  be the exact solution at times
be the exact solution at times  for
for 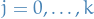 .
.
Then, subsituting  into the linear k-step method expression
into the linear k-step method expression
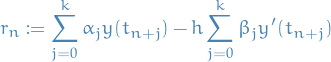
(which is actually the residual accumulated in the 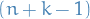 th step, but for notational convenience we will denote it
th step, but for notational convenience we will denote it  ).
).
A linear multistep method has order of consistency 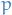 if (with
if (with  being the residual)
being the residual)

for all sufficiently smooth  , or (it can be shown) equivalently have the following properties:
, or (it can be shown) equivalently have the following properties:
Coeffiicents
 and
and  satisfy
satisfy
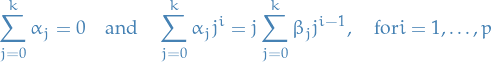
The polynomials
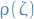 and
and  satisfy
satisfy

The polynomials
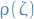 and
and  satisfy
satisfy
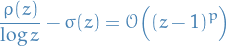
Unlike the single-step methods, e.g. Euler method, consistency is insufficient to ensure convergence!
Convergence
A linear multistep method is said to satisfy the root condition, if all roots  of
of

lie in the unit disc, i.e.  , and any root on the boundary, i.e.
, and any root on the boundary, i.e.  , has algebraic multiplicity one.
, has algebraic multiplicity one.
Otherwise, the modulus of the solution grows in time.
Suppose a linear multistep method is quipped with a starting procedure satisfying

Then the method converges to the exact solution of
![\begin{equation*}
\frac{dy}{dt} = f(t, y), \quad y(t_0) = y_0, \quad t \in [t_0, t_0 + T]
\end{equation*}](../../assets/latex/numerical_differential_equations_b738a47ef35fe06afe72dacf184c501b2dbee53f.png)
on a fixed interval as  if and only if it has order of accuracy
if and only if it has order of accuracy  and satisfies the root condition.
and satisfies the root condition.
Weak Stability and the Strong Root Condition
A convergent multistep method has to be:
- Consistent: so
 and
and  where
where  and
and  are the characteristic polynomials
are the characteristic polynomials Initialized with a convergent starting procedure: i.e. a method to compute
 for the first multistep iteration, to get started, satisfying
for the first multistep iteration, to get started, satisfying

- Zero-stable: i.e. it satisfies the root condition; the roots of
 are in the unit disc and simple if on the boundary.
are in the unit disc and simple if on the boundary.
If they're not simple, we get

as we iterate, which is a problem!
We refer to a multistep method that is zero-stable but which has some extraneous roots on the boundary of the unit disk as a weakly stable multistep method.
Same as root condition, but all roots which are not  are within the unit disk.
are within the unit disk.
Asymptotic Stability
The stability region 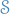 of a linear multistep method is the set of all points
of a linear multistep method is the set of all points  such that all roots
such that all roots  of the polynomial equation
of the polynomial equation

lie on the unit disc  , and those roots with modulues one are simple.
, and those roots with modulues one are simple.
On the boundary of the stability region 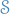 , precisely one root has modulus one, say
, precisely one root has modulus one, say 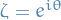 . Therefore an explicit representation for the boundary of
. Therefore an explicit representation for the boundary of 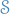 is:
is:
![\begin{equation*}
\partial \mathcal{S} = \left\{ z = \frac{\rho(e^{i \theta})}{\sigma(e^{i \theta})} : \theta \in [- \pi, \pi] \right\}
\end{equation*}](../../assets/latex/numerical_differential_equations_109fb547643b88491e8fa60c927989fdf4d39cf0.png)
This comes from applying the multistep method to the diff. eqn. (Dahlquist test equation)

Then

Letting 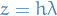 , we get
, we get
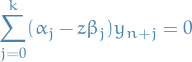
For any  , this is a recurrence relation / linear difference with characteristic polynomial
, this is a recurrence relation / linear difference with characteristic polynomial
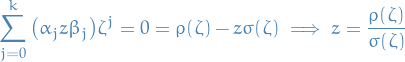
The stability region is  s.t. all roots of
s.t. all roots of 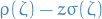 lie in the unit disc and those on the boundary are simply, which is just what we stated above.
lie in the unit disc and those on the boundary are simply, which is just what we stated above.
Geometric Integration
Focused on constructing methods for specific problems to account for properties of the system, e.g. symmetry.
Notation
First integrals
For some special functions  we may find that
we may find that  is constant along every solution to an /autonomous differential equation
is constant along every solution to an /autonomous differential equation

Such a function  is called a first integral.
is called a first integral.
This closely related to the conservation we in Hamiltonian physics.
Let
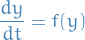
have a quadratic first integral. A Runge-Kutta method preserves this quadratic first integral if

Splitting methods
- Useful for constructing methods with specific properties
Suppose we wish to solve the differential equation
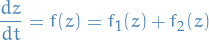
where each of the two differential equations

happen to be completely integrable (i.e. analytically solvable).
Then, any point in the phase space, the vector field can be written as two compontents  and
and  . We first step forward along one tangent, and then step forward in the second, each time for a small timestep
. We first step forward along one tangent, and then step forward in the second, each time for a small timestep  .
.
That is, we start from some point 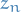 and solve first the IVP
and solve first the IVP
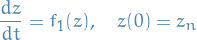
for time  , which takes us to the point
, which takes us to the point  where
where  represents the exact solution of the differential equations on vector field
represents the exact solution of the differential equations on vector field  .
.
Next, we start from  and solve the IVP
and solve the IVP

for time  , taking us to the point
, taking us to the point 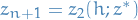 .
.
Denoting the flow maps of the vector fields  and
and  as
as  and
and  we have just computed
we have just computed

Such a method is called a splitting method.
The splitting method 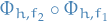 where
where  , has local error
, has local error
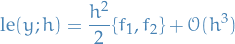
where 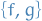 are the commutator of the vector fields
are the commutator of the vector fields  and
and  , which is another vector field
, which is another vector field
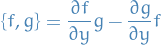
More generally
The splitting method 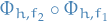 where
where  , has local error
, has local error
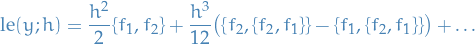
where 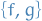 are the commutator of the vector fields
are the commutator of the vector fields  and
and 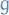 , which is another vector field
, which is another vector field
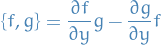
If the fields commute, i.e.  , then the splitting is exact.
, then the splitting is exact.



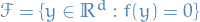 denotes the set of fixed points of the
denotes the set of fixed points of the 
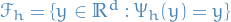 denotes the set of fixed points for the numerical estimation of the
denotes the set of fixed points for the numerical estimation of the  denotes the spectral radius of a matrix
denotes the spectral radius of a matrix 
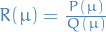 is the ratio between two polynomials
is the ratio between two polynomials  and
and  called the stability function
called the stability function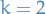 ) given by
) given by

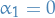 ,
, 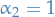 and
and 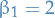 .
.