Differential Equations

Table of Contents

Stuff

Spectral method

A class of techniques to numerical solve certain differential equations. The idea is to write a solution of the differential equation as a sum of certain "basis functions" (e.g. Fourier Series which is a sum of sinouids) and then choose the coefficients in the sum in order to satisfy the differential equation as well as possible.

Series solutions

Definitions

Suppose we have a second-order differential equation of the form

\begin{equation*} P(x) y'' + Q(x) y' + R(x) y = 0 \end{equation*}

where $P$, $Q$ and $R$ are polynomials.

We then rewrite the equation as

\begin{equation*} y'' + p(x) y' + q(x) y = 0, \quad p(x) = \frac{Q(x)}{P(x)}, \quad q(x) = \frac{R(x)}{P(x)} \end{equation*}

Then we say the point $x_0$ is

  • an ordinary point if the functions $p(x) = P / Q$ and $q(x) = R / P$ are analytic at $x_0$
  • singular point if the functions aren't analytic

Convergence

Have a look at p. 248 in "Elementary Differential Equations and Boundary Problems". The two pages that follow summarizes a lot of different methods which can be used to determine convergence of a power series.

Systems of ODEs

Overview

The main idea here is to transform some n-th order ODE into a system of $n$ 1st order ODEs, which we can the solve using "normal" linear algebra!

Procedure

Consider an arbitrary n-th order ODE

\begin{equation*} y^{(n)} = F(y, y', \dots, y^{(n-1)}, t) \end{equation*}
  1. Change dependent variables to $x_1, x_2, \dots, x_n$ :
\begin{equation*} x_1 = y, \ x_2 = y', \ \dots \ , x_n = y^{(n-1)} \end{equation*}
  1. Take derivatives of the new variables
\begin{equation*} \begin{split} & x_1' = x_2, \ x_2' = x_3, \dots, x_{n-1}' = x_n \\ & x_n' = y^{(n)} = F(y, y', \dots, y^{(n-1)}, t) = F(x_1, x_2, \dots, x_n, t) \end{split} \end{equation*}

Homogenous

Fundamental matrices

Suppose that $\mathbf{x}^{(1)}(t), \mathbf{x}^{(2)}(t), \dots, \mathbf{x}^{(n)}(t)$ form a fundamental set of solutions for the equation

\begin{equation*} \mathbf{x}' = \mathbf{P} \mathbf{x} \end{equation*}

on some interval $\alpha < t < \beta$. Then the matrix

\begin{equation*} \mathbf{\Psi}(t) = \begin{pmatrix} x_1^{(1)} (t) & \dots & x_1^{(n)}(t) \\ \vdots & & \vdots \\ x_n^{(1)}(t) & \dots & x_n^{(n)}(t) \end{pmatrix} \end{equation*}

whose columns are the vectors $\mathbf{x}^{(1)}(t), \mathbf{x}^{(2)}(t), \dots, \mathbf{x}^{(n)}(t)$, is said to be a fundamental matrix for the system.

Note that the fundamental matrix is nonsingular / invertible since the solutions are lin. indep.

We reserve the notation $\boldsymbol{\Phi}(t)$ for the fundament matrices of the form

\begin{equation*} \boldsymbol{\Phi}(t) : \boldsymbol{\Phi}(t_0) = \begin{pmatrix} 1 & 0 & \dots & 0 \\ 0 & 1 & \dots & 0 \\ \vdots & \vdots & \ddots & 0 \\ 0 & 0 & \dots & 1 \end{pmatrix} = \mathbf{I} \end{equation*}

i.e. it's just a fundamental matrix parametrised in such a way that our initial conditions gives us the identity matrix.

The solution of an IVP of the form:

\begin{equation*} \mathbf{x}' = \mathbf{A} \mathbf{x}, \quad \mathbf{x}(0) = \mathbf{x}^0 \end{equation*}

can then be written

\begin{equation*} \mathbf{x} = \boldsymbol{\Phi}(t) \mathbf{x}^0 \end{equation*}

which can also be written

\begin{equation*} \mathbf{x}(t) = \exp(\mathbf{A} t) \mathbf{x}^0 \end{equation*}

Finally, we note that

\begin{equation*} \boldsymbol{\Phi}(t) = \boldsymbol{\Psi}(t) \boldsymbol{\Psi}^{-1}(t_0) \end{equation*}

The exponential of a matrix is given by

\begin{equation*} \exp (\mathbf{A} t) = \mathbf{I} + \sum_{n=1}^{\infty} \frac{\mathbf{A}^n t^n}{n!} \end{equation*}

and we note that it satisfies differential equations of the form

\begin{equation*} \mathbf{x}' = \mathbf{A} \mathbf{x} \end{equation*}

since

\begin{equation*} \frac{d}{dt} [ \exp(\mathbf{A} t) ] = \sum_{n=1}^{\infty} \frac{\mathbf{A}^n t^{n-1}}{(n - 1)!} = \mathbf{A} \Bigg[ \mathbf{I} + \sum_{n=1}^{\infty} \frac{\mathbf{A}^n t^n}{n!} \Bigg] = \mathbf{A} \exp(\mathbf{A} t) \end{equation*}

Hence, we can write the solution of the above differential equation as

\begin{equation*} \mathbf{x}(t) = \exp(\mathbf{A} t) \mathbf{x}^0 \end{equation*}
Repeating eigenvalues

Suppose we have a repeating eigenvalue $\rho = r$ (of algebraic multiplicity 2), with the found solution correspondig to $\rho$ is

\begin{equation*} \mathbf{x}^{(1)} = \boldsymbol{\xi} e^{\rho t} \end{equation*}

where $\boldsymbol{\xi}$ satisfies

\begin{equation*} (\mathbf{A} - \rho \mathbf{I}) \boldsymbol{\xi} = 0 \end{equation*}

We then assume the other solution to be of the form

\begin{equation*} \mathbf{x}^{(2)} = \boldsymbol{\xi} t e^{\rho t} + \boldsymbol{\eta} e^{\rho t} \end{equation*}

where $\boldsymbol{\eta}$ is determined by the equation

\begin{equation*} (\mathbf{A} - \rho \mathbf{I}) \boldsymbol{\eta} = \boldsymbol{\xi} \end{equation*}

Multiplying both sides by $(\mathbf{A} - \rho \mathbf{I})$ we get

\begin{equation*} (\mathbf{A} - \rho \mathbf{I})^2 \boldsymbol{\eta} = 0 \end{equation*}

since $(\mathbf{A} - \rho \mathbf{I}) \boldsymbol{\xi} = 0$ by definition. Solving the above equation for $\boldsymbol{\eta}$ and substituting that solution into the expression for $\mathbf{x}^{(2)}(t)$ we get the second solution corresponding to the repeated eigenvalue.

We call the vector $\boldsymbol{\eta}$ the generalized eigenvector of $\mathbf{A}$.

Non-homogenous

We want to solve the ODE systems of the form

\begin{equation*} \mathbf{x}' = P(t) \mathbf{x} + \mathbf{g}(t) \end{equation*}

Which has a general solution of the form

\begin{equation*} \mathbf{x}(t) = \sum_{i} c_i \mathbf{x}^{(i)}(t) + \mathbf{x}_{\text{par}}(t) \end{equation*}

where $\sum_{i} c_i \mathbf{x}^{(i)}(t)$ is the general solution to the corresponding homogenous ODE system.

We discuss the three methods of solving this:

  1. Diagonolisation
  2. Undetermined coefficients
  3. Variation of parameters
Diagonolisation

We assume the corresponding homogenous system is solved with the eigenvalues $r_i$ and eigenvectors $\boldsymbol{\xi}^{(i)}$, and then introduce the change of variables $\mathbf{x} = T \mathbf{y}$ :

\begin{equation*} \begin{split} T \mathbf{y}' &= A T \mathbf{y} + \mathbf{g}(t) \\ \implies \mathbf{y}' &= T^{-1} A T \mathbf{y} + T^{-1} \mathbf{g} \\ \iff \mathbf{y}' &= D \mathbf{y} + \mathbf{h} \end{split} \end{equation*}

which gives us a system of $n$ decoupled systems:

\begin{equation*} y_i' = r_i y_i(t) + h_i(t) \implies y_i(t) = c_i e^{r_i t} + e^{r_i t} \int_0^t e^{-r_i s} h_i(s) \ ds \end{equation*}

and finally we transform back to the original variables:

\begin{equation*} \mathbf{x}(t) = T \mathbf{y}(t) \end{equation*}
  • Example

    Consider

    \begin{equation*} \mathbf{x}' = A \mathbf{x} + \mathbf{g} = \begin{pmatrix} -2 & 1 \\ 1 & -2 \end{pmatrix} \mathbf{x} + \begin{pmatrix} 2 e^{-t} \\ 3t \end{pmatrix} \end{equation*}

    Since the system is linear and non-homogeneous, the general solution must be of the form

    \begin{equation*} \mathbf{x}(t) = c_1 \mathbf{x}^{(1)} + c_2 \mathbf{x}^{(2)} + \mathbf{x}_p(t) \end{equation*}

    where $\mathbf{x}_p(t)$ denotes the particular solution.

    The homogenous solution can be found as follows:

    \begin{equation*} \begin{vmatrix} -2 - r & 1 \\ 1 & -2 - r \end{vmatrix} = r^2 + 4 r + 3 = (r + 3)(r + 1) = 0 \end{equation*}

    When $\textcolor{red}{r = - 3}$: if $\boldsymbol{\xi}_{-3} = \begin{pmatrix} x \\ y \end{pmatrix} \implies y = -x$, hence we choose

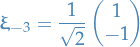
    \begin{equation*} \boldsymbol{\xi}_{-3} = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ -1 \end{pmatrix} \end{equation*}

    When $\textcolor{red}{r = -1}$: if $\boldsymbol{\xi}_{-1} = \begin{pmatrix} x \\ y \end{pmatrix} \implies y = x$, hence we choose

    \begin{equation*} \boldsymbol{\xi}_{-1} = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 1 \end{pmatrix} \end{equation*}

    Thus, the general homogenous solution is:

    \begin{equation*} \mathbf{x}_h(t) = c_1 e^{-3t} \boldsymbol{\xi}_{-3} + c_2 e^{-t} \boldsymbol{\xi}_{-1} \end{equation*}

    To find the particular solution, we make the change of variables $\textcolor{red}{\mathbf{x} = T \mathbf{y}}$:

    \begin{equation*} T = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ -1 & 1 \end{pmatrix} \implies T^{-1} = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & -1 \\ 1 & 1 \end{pmatrix} \end{equation*}

    With the new variables the ODE looks as follows:

    \begin{equation*} \begin{split} \frac{d \mathbf{y}}{d t} &= \begin{pmatrix} -3 & 0 \\ 0 & -1 \end{pmatrix} \mathbf{y} + T^{-1} \mathbf{g} \\ &= \begin{pmatrix} -3 & 0 \\ 0 & -1 \end{pmatrix} \mathbf{y} + \frac{1}{\sqrt{2}} \begin{pmatrix} 2e^{-3t} - 3t \\ 2e^{-t} + 3t \end{pmatrix} \end{split} \end{equation*}

    Which in terms of $\mathbf{y}^T = (y_1, y_2)$ is

    \begin{equation*} \begin{split} y_1' + 3y_1 &= \sqrt{2} e^{-3t} - \frac{3}{\sqrt{2}} t \\ y_2' + y_2 &= \sqrt{2} e^{-t} + \frac{3}{\sqrt{2}} t \end{split} \end{equation*}

    Which, by the use of undetermined coefficients, we can solve as

    \begin{equation*} \begin{split} y_1(t) &= c_1 e^{-3t} + ae^{-t} + b t + c \\ y_2(t) &= c_2 e^{-t} + f t e^{-t} + ht + m \end{split} \end{equation*}

    Doing "some" algebra, we eventually get

    \begin{equation*} \begin{split} y_1(t) &= c_1 e^{-3t} + \frac{1}{\sqrt{2}} e^{-t} - \frac{3}{\sqrt{2}} \Bigg( \frac{t}{3} - \frac{1}{9} \Bigg) \\ y_2(t) &= c_2 e^{-t} + \sqrt{2} t e^{-t} + \frac{3}{\sqrt{2}} (t - 1) \end{split} \end{equation*}

    Then, finally, substituting back into the equation for $\mathbf{x} = T \mathbf{y}$, and we would get the final result.

Undetermined coefficients

This method only works if the coefficient matrix $\mathbf{P}(t) = \mathbf{A}$ for some constant matrix $\mathbf{A}$, and the components of $\mathbf{g}$ are polynomial, exponential, or sinusoidal functions, or sums or products of these.

Variation of parameters

This is the most general way of doing this.

Suppose we have the n-th order linear differential equation

\begin{equation*} L[y] = y^{(n)} + p_1(t) y^{(n - 1)} + \dots + p_{n - 1}(t) y' + p_n(t)y = g(t) \end{equation*}

Suppose we have found the solutions to the corresponding homogenous diff. eqn.

\begin{equation*} y_h(t) = c_1 y_1(t) + c_2 y_2(t) + \dots + c_n y_n(t) \end{equation*}

With the method of variation of parameters we seek a particular solution of the form

\begin{equation*} y_p(t) = u_1(t) y_1(t) + u_2(t) y_2(t) + \dots + u_n(t) y_n(t) \end{equation*}

Since we have $n$ functions $u_i(t)$ to determine we have to specify $n$ conditions.

One of these conditions is cleary that we need to satisfy the non-homongenous diff. eqn. above. Then the $n - 1$ other conditions are chosen to make the computations as simple as possible.

Taking the first partial derivative wrt. $t$ of $y_p$ we get (using the product rule)

\begin{equation*} y_p' = (u_1' y_1 + \dots + u_n' y_n) + (u_1 y_1' + \dots + u_n y_n') \end{equation*}

We can hardly expect it to be simpler to determine $y_p$ if we have to solve diff. eqns. of higher order than what we started out with; hence we try to surpress the terms that lead to higher derivatives of $u_1, \dots, u_n$ by imposing the following condition

\begin{equation*} u_1' y_1 + \dots + u_n' y_n = 0 \end{equation*}

which we can do since we're just looking for some arbitrary functions $u_i$. The expression for $y_p'$ then reduces to

\begin{equation*} y_p' = u_1 y_1' + \dots + u_n y_n' \end{equation*}

Continuing this process for the derivatives $y_p'', \dots, y_p^{(n - 1)}$ we obtain our $n - 1$ condtions:

\begin{equation*} u_1' y_1^{(m)} + \dots + u_n' y_n^{(n)} = 0, \quad m = 1, 2, \dots, n - 2 \end{equation*}

giving us the expression for the m-th derivative of $y_p$ to be

\begin{equation*} y_p^{(m)} = u_1 y_1^{(m)} + \dots + u_n y_n^{(m)}, \quad m = 2, 3, \dots, n - 1 \end{equation*}

Finally, imposing that $y_p^{(n)}$ has to satisfy the original non-homogenous diff. eqn. we take the derivative of $y_p^{(n - 1)}$ and substitute back into the equation. Doing this, and grouping terms involving each of $y_i$ together with their derivatives, most of the terms drop out due to $y_i$ being a solution to the homogenous diff. eqn., yielding

\begin{equation*} u_1' y_1 + \dots + u_n' y_n = g \end{equation*}

Together with the previous $n - 1$ conditons we end up with a system of linear equations

\begin{equation*} \begin{cases} y_1 u_1' + \dots y_n u_n' &= 0 \\ y_1' u_1' + \dots y_n' u_n' &= 0 \\ & \vdots \\ y_1^{(n - 1)} u_1' + \dots y_n^{(n - 1)} u_n' &= g \\ \end{cases} \end{equation*}

(note the $g$ at the end!).

The sufficient condition for the existence of a solution of the system of equations is that the determinant of coefficients is nonzero for each value of $t$. However, this is guaranteed since $\{y_i\}$ form a fundamental set of solutions for the homogenous eqn.

In fact, using Cramers rule we can write the solution of the system of equations in the form

\begin{equation*} u_m'(t) = \frac{g(t) W_m(t)}{W(t)}, \quad m = 1, 2, \dots, n \end{equation*}

where $W_m$ is the determinant of obtained from $W$ by replacing the m-th column by $(0, 0, \dots, 1)^T$. This gives us the particular solution

\begin{equation*} y_p(t) = \sum_{m=1}^{n} y_m(t) \int_{t_0}^t \frac{g(s) W_m(s)}{W(s)} \ ds \end{equation*}

where $t_0$ is arbitrary.

Assume that a fundamental matrix $\mathbf{\Psi}(t)$ for the corresponding homogenous system

\begin{equation*} \mathbf{x}' = \mathbf{P}(t) \mathbf{x} \end{equation*}

has been found. We can then use the method of variation of parameters to construct a particular solution, and hence the general solution, of the non-homogenous system.

The general solution to the homogenous system is $\mathbf{\Psi}(t) \mathbf{c}$, we seek a solution to the non-homogenous system by replacing the constant vector $\mathbf{c}$ by a vector function $\mathbf{u}(t)$. Thus we assume that

\begin{equation*} \mathbf{x} = \mathbf{\Psi}(t) \mathbf{u}(t) \end{equation*}

is a solution, where $\mathbf{u}(t)$ is a vector function to be found.

Upon differentiating $\mathbf{x}$ we get

\begin{equation*} \mathbf{\Psi}'(t) \mathbf{u}(t) + \mathbf{\Psi}(t) \mathbf{u}'(t) = \mathbf{P}(t) \mathbf{\Psi}(t) \mathbf{u}(t) + \mathbf{g}(t) \end{equation*}

Since $\mathbf{\Psi}(t)$ is a fundamental matrix, $\mathbf{\Psi}'(t) = \mathbf{P}(t) \mathbf{\Psi}(t)$; hence the above expression reduces to

\begin{equation*} \mathbf{\Psi}(t) \mathbf{u}'(t) = \mathbf{g}(t) \end{equation*}

Since $\mathbf{\Psi}(t)$ is nonsingular (i.e. invertible) on any interval where $\mathbf{P}(t)$ is continuous. Hence $\mathbf{\Psi}^{-1}(t)$ exists, and therefore

\begin{equation*} \mathbf{u}'(t) = \mathbf{\Psi}^{-1}(t) \mathbf{g}(t) \end{equation*}

Thus for $\mathbf{u}(t)$ we can select any vector from the class of vectors which satisfy the previous equation. These vectors are determined only up to an arbitrary additive constant vector; therefore, we denote $\mathbf{u}(t)$ by

\begin{equation*} \mathbf{u}(t) = \int \mathbf{\Psi}^{-1}(t) \mathbf{g}(t) dt + \mathbf{c} \end{equation*}

where the constant vector $\mathbf{c}$ is arbitrary.

Finally, this gives us the general solution for a non-homogenous system

\begin{equation*} \mathbf{x} = \mathbf{\Psi}(t) \mathbf{c} + \mathbf{\Psi}(t) \int_{t_0}^{t_1} \mathbf{\Psi}^{-1}(s) \mathbf{g}(s) ds \end{equation*}

Dynamical systems

In $\mathbb{R}^n$, an arbitrary autonomous dynamical system can be written as

\begin{equation*} \dot{y} = g(y) \end{equation*}

for some smooth $g(y): \mathbb{R}^n \to \mathbb{R}^n$, for a the 2D case:

\begin{equation*} \frac{dx}{dt} = F(x, y), \quad \frac{dy}{dt} = G(x, y) \end{equation*}

which in matrix notation we write

\begin{equation*} \frac{d \mathbf{x}}{d t} = \mathbf{f}(\mathbf{x}), \quad \mathbf{x}(t_0) = \mathbf{x}_0 \end{equation*}

Notation

  • $\mathbf{x}^0$ denotes a critical point
  • $\mathbf{f}(\mathbf{x})$ denotes the RHS of the autonomous system
  • $\mathbf{x} = \boldsymbol{\phi}(t)$ denotes a specific solution

Theorems

The critical point $\mathbf{x} = \mathbf{0}$ of the linear system

\begin{equation*} \mathbf{x}' = \mathbf{A} \mathbf{x} \end{equation*}

where we suppose $\mathbf{A}$ has eigenvalues $r_1, r_2$, is:

  • asymptotically stable if $r_1, r_2$ are real and negative
  • stable if $r_1, r_2$ are pure imaginary
  • unstable if $r_1, r_2$ are real and either positive, or have positive real part

Stability

The points $\mathbf{f}(\mathbf{x}) = 0$ are called critical points of the autonomous system

\begin{equation*} \mathbf{x}' = \mathbf{f}(\mathbf{x}) \end{equation*}

Let $\mathbf{x}^0$ be a critical point of the system.

  • $\mathbf{x}^0$ is said to be stable if for any $\varepsilon > 0$,

    \begin{equation*} \exists \delta > 0 : || \boldsymbol{\phi}(0) - \mathbf{x}^0 || < \delta \implies || \boldsymbol{\phi}(t) - \mathbf{x}^0 || < \varepsilon \end{equation*}

    for all $t \ge 0$. I.e. for some solution $\boldsymbol{\phi}(t)$ we parametrize it such that $||\boldsymbol{\phi}(0) - \mathbf{x}^0|| < \delta$ for some $\delta > 0$ such that we stay close to $\mathbf{x}^0$ for all $t \ge 0$, then we say it's stable.

  • $\mathbf{x}^0$ is said to be asymptotically stable if it's stable and there exists a $\delta_0 > 0$ s.t. that if a solution $\mathbf{x} = \boldsymbol{\phi}(t)$ satisfies

    \begin{equation*} || \boldsymbol{\phi}(0) - \mathbf{x}^0 || < \delta_0 \end{equation*}

    then

    \begin{equation*} \underset{t \to \infty}{\lim} \boldsymbol{\phi}(t) = \mathbf{x}^0 \end{equation*}

    i.e. if we start near $\mathbf{x}^0$, the limiting behaviour converges to $\mathbf{x}^0$. Note that this is stronger than just being stable.

  • $\mathbf{x}^0$ which is NOT stable, is of course unstable.

Intuitively what we're saying here is that:

  • for any $\varepsilon > 0$ we can find a trajectory (i.e. solution with a specific initial condition, thus we can find some initial condition ) such that the entire trajectory stays within $\varepsilon > 0$ of the critical points for all $t > 0$.

When we say a critical point is isolated, we mean that there are no other critical points "nearby".

In the case of a system

\begin{equation*} \mathbf{x}' = \mathbf{A} \mathbf{x} + \mathbf{g}(\mathbf{x}) \end{equation*}

By solving the equation

\begin{equation*} \mathbf{A} \mathbf{x} = \mathbf{0} \end{equation*}

if the solution $\mathbf{x}^0$ is a single vector, rather than a line or plane, the critical point $\mathbf{x}^0$ is not isolated.

Suppose that we have the system

\begin{equation*} \mathbf{x}' = \mathbf{A} \mathbf{x} + \mathbf{g}(\mathbf{x}) \end{equation*}

and that $\mathbf{x}^0$ is a isolated critical point of the system. We also assume that $\det \mathbf{A} \ne 0$ so that $\mathbf{x}^0$ is also a isolated critical point of the linear system $\mathbf{x}' = \mathbf{A} \mathbf{x}$. If

\begin{equation*} \frac{|| \mathbf{g}(\mathbf{x}) ||}{|| \mathbf{x} ||} \to 0 \quad \text{ as } \quad \mathbf{x} \to \mathbf{0} \end{equation*}

that is, $||\mathbf{g}(\mathbf{x})||$ is small in comparison to $||\mathbf{x}||$ near the critical point $\mathbf{x}^0$, we say the system is a locally linear system in the neighborhood of the critical point $\mathbf{x}^0$.

Linearized system

In the case where we have a locally linear system, we can approximate the system near isolated critical points by instead considering the Jacobian of the system. That is, if we have the dynamical system

\begin{equation*} \mathbf{x}' = \mathbf{f}(\mathbf{x}) \end{equation*}

with a critical point at $\mathbf{x}_0$, we can use the linear approximation of $\mathbf{f}$ near $\mathbf{x}_0$:

\begin{equation*} \mathbf{f}(\mathbf{x}) = \mathbf{f}(\mathbf{x}_0) + D_{\mathbf{f}}(\mathbf{x}_0) (\mathbf{x} - \mathbf{x}_0) \end{equation*}

where $D_{\mathbf{f}}$ denotes the Jacobian of $\mathbf{f}$, which is

\begin{equation*} D_{\mathbf{f}}(\mathbf{x}) = \begin{pmatrix} \frac{\partial f_m}{\partial x_n}\big|_{\mathbf{x}} \end{pmatrix} \end{equation*}

Substituting back into the ODE

\begin{equation*} \mathbf{x}' = \mathbf{f}(\mathbf{x}_0) + D_{\mathbf{f}}(\mathbf{x}_0)(\mathbf{x} - \mathbf{x}_0) = \mathbf{x}_0' + D_{\mathbf{f}}(\mathbf{x}_0)(\mathbf{x} - \mathbf{x}_0) \end{equation*}

Letting $\mathbf{y} = \mathbf{x} - \mathbf{x}_0$, we can rewrite this as

\begin{equation*} \mathbf{y}' = D_{\mathbf{f}}(\mathbf{x}_0) \mathbf{y} \end{equation*}

which, since $D_{\mathbf{f}}(\mathbf{x}_0)$ is constant given $\mathbf{x}_0$, gives us a linear ODE wrt $\mathbf{y}$, hence the name linearization of the dynamical system.

Hopefully $D_{\mathbf{f}}(\mathbf{x}_0) \mathbf{y}$ is a simpler expression than what we started out with.

General procedure
  1. Obtain critical points, i.e. $\mathbf{x}' = 0$
  2. If non-linear and locally linear, compute the Jacobian and use this is an linear approximation to the non-linear system, otherwise: do nothing.
  3. Inspect the following to determine the behavior of the system:
    • $\det \mathbf{A} = \prod_{i=1}^n \lambda_i$ and $\tr \mathbf{A} = \sum_{i=1}^{n} \lambda_i$
    • Compute eigenvalues and eigenvectors to obtain solution of the (locally) linear system
    • Consider asymptotic behavior of the different terms in the general solution, i.e. $t \to \pm \infty$
    • $\frac{d y}{d x} = \frac{dy / dt}{dx / dt}$ which provides insight into the phase diagram / surface. If non-linear, first do for linear approx., then for non-linear system
Points of interest

The following section is a very short summary of Ch. 9.1 [Boyce, 2013]. Look here for a deeper look into what's going on, AND some nice pictures!

Here we consider 2D systems of 1st order linear homogenous equations with constant coefficients:

\begin{equation*} \frac{d \mathbf{x}}{dt} = \mathbf{A} \mathbf{x} \end{equation*}

where $\mathbf{A}_{2 \times 2}$ and $\mathbf{x}_{2 \times 1}$. Suppose $r_1, r_2$ are the eigenvalues for the matrix $\mathbf{A}$, and thus gives us the expontentials for the solution $\mathbf{x}(t)$.

We have multiple different cases which we can analyse:

  • $r_1, r_2 \in \mathbb{R}, \quad r_1 \ne r_2, \quad \text{sign}(r_1) = \text{sign}(r_2)$:
    • Exponential decay: node or nodal sink
    • Exponential growth. node or nodal source
  • $r_1, r_2 \in \mathbb{R}, \quad \text{sign}(r_1) \ne \text{sign}(r_2)$: saddle point
  • $r_1 = r_2$:
    • two independent eigenvectors: proper node (sometimes a star point )
    • one independent eigenvector: improper or degenerate node
  • $r_1 = \lambda + i \mu, \quad r_2 = \lambda - i \mu, \quad \lambda \ne 0$: spiral point
    • spiral sink refers to decaying spiral point
    • spiral source refers to growing spiral point
  • $r_1, r_2 = \pm i \mu$: center
Basin of attraction

This denotes the set of all points $P$ in the xy-plane s.t. the trajectory passing through $P$ approaches the critical point as $t \to \infty$.

A trajectory that bounds the basin of attraction is called a separatix.

Limit cycle

Limit cycles are periodic solutions such that at least one other non-closed trajectory asymptotes to them as $t \to \infty$ and / or $t \to - \infty$.

Let $F(x, y)$ and $G(x, y)$ have continuous first partial derivatives in a simply connected domain $D$.

If $\partial_x F + \partial_y G$ has the same sign in the entire $D$, then there are no closed trajectories in $D$.

Consider the system

\begin{equation*} \dot{x} = F(x, y), \quad \dot{y} = G(x, y) \end{equation*}

Let $F(x, y)$ and $G(x, y)$ have continious first partial derivatives in a domain $D$.

Let $D_1$ be a bounded subdomain of $D$ and let $R = D_1 \cap \partial D_1$. Suppose $R$ contains no critical points.

If

\begin{equation*} \exists \mathbf{x}(t) : \mathbf{x}(t) \in R, \quad \forall t \ge t_0 \end{equation*}

then

  • solution is periodic (closed trajectory)
  • OR it spirals towards a closed trajectory

Hence, there exists a closed trajectory.

Where

  • $\mathbf{x}(t)$ denotes a particular trajectory
  • $\partial D_1$ denotes the boundary of $D_1$
Useful stuff
\begin{equation*} \begin{split} r \dot{r} &= x \dot{x} + y \dot{y} \\ - r^2 \dot{\theta} &= y \dot{x} - x \dot{y} \end{split} \end{equation*}
  • Example

    Say we have the following system:

    \begin{equation*} \dot{x} = - y + x \frac{f(r)}{r}, \quad \dot{y} = x + y \frac{f(r)}{r} \end{equation*}

    where $r^2 = x^2 + y^2$, has periodic solutions corresponding to the zeroes of $f(r)$. What is the direction of the motion on the closed trajectories in the phase plane?

    Using the identities above, we can rewrite the system as

    \begin{equation*} \dot{r} = f(r), \quad \dot{\theta} = 1 \end{equation*}

    Which tells us that the trajectories are moving in counter-clockwise direction.

Lyapunov's Second Method

Goal is to obtain information about the stability or instability of the system without explicitly obtaining the solutions of the system. This method allows us to do exactly that through the construction of a suitable auxillary function, called the Lyapunov function.

For the 2D-case, we consider such a function of the following form:

\begin{equation*} \dot{V}(x, y) = V_x(x, y) F(x, y) + V_y(x, y) G(x, y) \end{equation*}

where $F(x, y)$ and $G(x, y)$ are as given in the autonomous system definition.

We choose the notation above because $\dot{V}$ can be identified as the rate of change of $V$ along the trajectory of the system that passes through the point $(x, y)$. That is, if $x = \phi(t), y = \psi(t)$ is a solution of the system, then

\begin{equation*} \begin{split} \frac{d V[\phi(t), \psi(t)]}{d t} &= V_x [\phi(t), \psi(t)] \frac{d \phi(t)}{dt} + V_y [\phi(t), \psi(t)] \frac{d \psi(t)}{dt} \\ &= V_x(x, y) F(x, y) + V_y(x, y) G(x, y) \\ &= \dot{V}(x, y) \end{split} \end{equation*}

Suppose that the autonomous system has an isolated critical point at the origin.

If there exists a continuous and positive definite function $V$ which also has continuous first partial derivatives $\dot{V}$:

  • if $\dot{V}(x, y) < 0, \quad \dot{V}(0, 0) = 0$ ( negative definite ) on some domain $D$, then the origin is an asymptotically stable critical point
  • if $\dot{V}(x, y) \le 0$ ( negative semidefinite ) then the origin is a stable point

Suppose that the autonomous system has an isolated critical point at the origin.

Let $V$ be a function that is continuous and has continuous first partial derivatives.

Suppose that $V(0, 0) = 0$ and that in every neighborhood of the origin there is a least one point at which $V$ is positive (negative). If there exists a domain $D$ containing the origin such that the function $\dot{V}$ is positive definite ( negative definite ) on $D$, then the origin is an unstable point.

Let the origin be an isolated critical point of the autonomous system. Let the function $V$ be continous and have continuous first partial derivatives. If there is a bounded domain $D_K$ containing the origin where $V(x, y) < K$ for some positive $K$, $V$ is positive definite and $\dot{V}$ is negative definite , and then every solution of the system that starts at a point in $D_K$ approaches the origin as $t \to \infty$.

We're not told how to construct such a function. In the case of a physical system, the actual energy function would work, but in general it's more trial-and-error.

Lyapunov function

Lyapunov functions are scalar functions which can be used to prove stability of an equilibrium of an ODE.

Lyapunov's Second Method (alternative)

Notation
Definitions

Let $V: \mathbb{R}^n \to \mathbb{R}$ be a continuous scalar function.

$V$ is a Lyapunov-candidate-function if it's /locally positive-definite function, i.e.

\begin{equation*} V(\mathbf{0}) = 0, \quad \mathbf{V}(\mathbf{x}) > 0, \quad \forall \mathbf{x} \in U \ \backslash \{ \mathbf{0} \} \end{equation*}

with $U$ bein a neighborhood region around $\mathbf{0}$.

Further, let $\mathbf{x}_0 = \mathbf{0}$ be a critical or equilibrium point of the autonomous system

\begin{equation*} \dot{\mathbf{x}} = \frac{d \mathbf{x}}{dt} = \mathbf{f}(\mathbf{x}) \end{equation*}

And let

\begin{equation*} \dot{V}(\mathbf{x}) = \frac{d}{dt} V \Big( \mathbf{x}(t) \Big) = \frac{\partial V}{\partial \mathbf{x}} \frac{\partial \mathbf{x}}{\partial t} = \boldsymbol{\nabla} V \cdot \dot{\mathbf{x}} = \boldsymbol{\nabla} V \cdot \mathbf{f}(\mathbf{x}) \end{equation*}

Then, we say that the Lyapunov-candidate-function $V(\mathbf{x})$ is a Lyapunov function of the system if and only if

\begin{equation*} \dot{V} \Big( \mathbf{x}(t) \Big) \le 0, \quad \forall t > 0 \end{equation*}

where $\mathbf{x}(t)$ denotes a specific trajectory of the system.

For a given autonomous system, if there exists a Lyapunov function $V(\mathbf{x})$ in some neigborhood $U$ of some critical / equilibrium point $\mathbf{x}_0$, then the system is stable (in a Lyapunov sense).

Further, if $\dot{V}$ is negative-definite, i.e. we have a strict inequality

\begin{equation*} \dot{V} \Big( \mathbf{x}(t) \Big) < 0 \quad \forall t > 0 \end{equation*}

then the system is asymptotically stable about the critical / equilibrium point $\mathbf{x}_0$.

When talking about critical / equilibrium point $\mathbf{x}_0$, when considering a Lyapunov function, we have to make sure that the critical point corresponds to $\mathbf{0}$ . This can easily be achieved by "centering" the system about the point original critical point $\mathbf{x}_0$, i.e. creating some new system with $\tilde{\mathbf{x}} = \mathbf{x} - \mathbf{x}_0$, which will then have the corresponding critical point at $\tilde{\mathbf{x}}_0 = 0$.

Observe that this in no way affects the qualitative analysis of the critical point.

Let $V: \mathbb{R}^n \to \mathbb{R}$ be a continuous scalar function.

$V$ is a Lyapunov-candidate-function if it's a locally postitive-definite function, i.e.

\begin{equation*} V(\mathbf{0}) = 0, \quad V(\mathbf{x}) > 0, \quad \forall x \in U \backslash \{ 0 \} \end{equation*}

with $U$ being a neighborhood region around $\mathbf{x} = \mathbf{0}$.

Let $\mathbf{x}_0 = \mathbf{0}$ be a critical / equilibrium point of the autonomous system

\begin{equation*} \dot{\mathbf{x}} = \frac{d \mathbf{x}}{dt} = f(\mathbf{x}) \end{equation*}

And let

\begin{equation*} \dot{V}(\mathbf{x}) = \frac{d}{dt} V \big( \mathbf{x}(t) \big) = \frac{\partial V}{\partial \mathbf{x}} \cdot \frac{d \mathbf{x}}{d t} = \nabla V \cdot \dot{\mathbf{x}} = \nabla V \cdot f(\mathbf{x}) \end{equation*}

be the time-derivative of the Lyapunov-candidate-function $V$.

Let $V$ be a locally positive definite function (a candidate Lyapunov function) and let $\dot{V}$ be its derivative wrt. time along the trajectories of the system.

If $\dot{V}$ is locally negative semi-definite, then $V$ is called a Lyapunov function of the system.

If there exists a Lyapunov function $\mathbf{V}$ of a system, then $\mathbf{x}_0 = 0$ is a stable equilibrium point in the sense of Lyapunov.

If in addition $\dot{V}(\mathbf{x}) < 0$ and $0 < ||\mathbf{x}|| < r_1$ for some $r_1$, i.e. $\dot{V}$ is locally negative definite , then $\mathbf{x}_0 = \mathbf{0}$ is asymptotically stable.

Remember, we can always re-parametrize a system to be centered around a critical point, and come to an equivalent analysis of the system about the critical point, since we're simply "adding" a constant.

Proof

First we want to prove that if $V$ is a Lyapunov function then $\mathbf{x}_0 = \mathbf{0}$ is a stable critical point.

Suppose $\varepsilon > 0$ is given. We need to find $\delta > 0$ such that for all $||\mathbf{x}(0)|| < \delta$, it follows that $||\mathbf{x}(t)|| < \varepsilon, \ \forall t > 0$.

Then let $\varepsilon_1 = \min \{ \varepsilon, r \}$, where $r$ is the radius of a ball describing the "neighborhood" were we know that $V(\mathbf{x})$ is a Lyapunov candidate function, and define

\begin{equation*} m = \min_{||\mathbf{x}|| = \varepsilon_1} V(\mathbf{x}) \end{equation*}

Since $V(\mathbf{x})$ is continuous, the above $m$ is well-defined and positive.

Choose $\delta$ satisfying $0 < \delta < \varepsilon_1$ such that for all $||\mathbf{x}|| < \delta, \ V(\mathbf{x}) < m$. Such a choise is always possible, again because of the continuity of $V(\mathbf{x})$.

Now, consider any $\mathbf{x}(0)$ such that $|| \mathbf{x}(0) || < \delta$ and thus $V \big( \mathbf{x}(0) \big) < m$ and let $\mathbf{x}(t)$ be the resulting trajectory. Observe that $V \big( \mathbf{x}(t) \big)$ is non-increasing, that is

\begin{equation*} \dot{V} \big( \mathbf{x}(t) \big) \le 0 \end{equation*}

which results in $V \big( \mathbf{x}(t) \big) < m$.

We will now show that this implies that $||\mathbf{x}(t)|| < \varepsilon_1$, for a trajectory defined such that $||\mathbf{x}(0)|| < \delta$ and thus $|| V \big( \mathbf{x}(t) \big) || < m$ as described above.

Suppose there exists $t_1$ such that $|| \mathbf{x}(t_1) || > \varepsilon_1$, then since we're assuming $\mathbf{x}(t)$ is such that

\begin{equation*} \mathbf{x}(t) : ||\mathbf{x}(0)|| < \delta \quad \implies \quad V \big( \mathbf{x}(t) \big) < \min_{|| \mathbf{x} || = \varepsilon_1} || V(\mathbf{x})|| = m \end{equation*}

as described above, then clearly we also have

\begin{equation*} ||\mathbf{x}(t_1)|| < m \end{equation*}

Further, by continuity (more specifically, the IVT) we must have that at an earlier time $t_2$ we had

\begin{equation*} ||\mathbf{x}(t_2)|| = \varepsilon_1 \end{equation*}

But since $t_2 < t_1$, we clearly have

\begin{equation*} V \big( \mathbf{x}(t_2) \big) \le V \big( \mathbf{x}(t_1) \big) \end{equation*}

due to $\dot{V} \le 0$. But the above implies that

\begin{equation*} V \big( \mathbf{x}(t_2) \big) < m = \min_{|| \mathbf{x} || = \varepsilon_1} || V(\mathbf{x})|| \end{equation*}

Which is a contradiction, since $||\mathbf{x}(t_2)|| = \varepsilon_1$ implying that $V \big( \mathbf{x}(t_2) \big) \le m$.

Now we prove the theorem for asymptotically stable solutions! As stated in the theorem, we're now assuming $\dot{V}$ to be locall negative-definite, that is,

\begin{equation*} \dot{V}(\mathbf{x}) < 0, \quad \forall x \in U \end{equation*}

We then need to show that

\begin{equation*} V \big( \mathbf{x}(t) \big) \to 0 \quad \text{as} \quad t \to \infty \end{equation*}

which by continuity of $V$, implies that $||\mathbf{x}|| \to 0$.

Since $V \big( \mathbf{x}(t) \big)$ is strictly decreasing and $V \big( \mathbf{x}(t) \big) \ge 0$ we know that

\begin{equation*} V \big( \mathbf{x}(t) \big) \to c, \quad c \ge 0 \end{equation*}

And we then want to show that $c = 0$. We do this by /contradiction.

Suppose that $c > 0$. Let the set $S$ be defined as

\begin{equation*} S = \{ \mathbf{x} \in \mathbb{R}^n \mid V(\mathbf{x}) \le c\} \end{equation*}

and let $B_\alpha$ be a ball inside $S$ of radius $\alpha$, that is,

\begin{equation*} B_\alpha = \{ \mathbf{x} \in S \mid ||\mathbf{x}|| < \alpha\} \end{equation*}

Suppose $\mathbf{x}(t)$ is a trajectory of the system that starts at $\mathbf{x}(0)$.

We know that $V \big( \mathbf{x}(t) \big)$ is decreasing monotonically to $c$ and $V \big( \mathbf{x}(t) \big) > c$ for all $t$. Therefore, $\mathbf{x}(t) \notin B_\alpha$, since $B_\alpha \subset S$ which is defined as all elements for which $V(\mathbf{x}) \le c$ (and to drive the point home, we just established that the $V \big( \mathbf{x}(t) \big) > c$).

In the first part of the proof, we established that

\begin{equation*} \mathbf{x}(0) < \delta \quad \implies \quad || \mathbf{x}(t) || < \varepsilon \end{equation*}

We can define the largest derivative of $V(\mathbf{x})$ as

\begin{equation*} - \gamma = \max_{\alpha \le || \mathbf{x} || \le \varepsilon} \dot{V}(\mathbf{x}), \quad \gamma > 0 \end{equation*}

Clearly, $- \gamma < 0$ since $\dot{V}(\mathbf{x})$ is locally negative-definite. Observe that,

\begin{equation*} \begin{split} V \big( \mathbf{x}(t) \big) &= V \big( \mathbf{x}(0) \big) + \int_{0}^{t} \dot{V} \big( \mathbf{x}(\tau) \big) \ d \tau \\ &\le V \big( \mathbf{x}(0) \big) - \gamma t \end{split} \end{equation*}

which implies that $V \big( \mathbf{x}(t) \big) < 0$, resulting in a contradiction established by the $c > 0$, hence $c = 0$.

Remember that in the last step where say suppose "there exists $t_1$ such that $\norm{\mathbf{x}(t_1)} > \varepsilon_1$" we've already assumed that the initial point of our trajectory, i.e. for $\mathbf{x}(0)$, was within a distance $\varepsilon_1$ from the critical point $\mathbf{x}_0$! Thus we would have to cross the "boundary" defined by $\varepsilon_1$ from $\mathbf{x}_0$.

Therefore, intuitively, we can think of the Lyapunov function providing a "boundary" which the solution will not cross given it starts with this "boundary"!

Side-notes
  • When reading about this subject, often people will refer to Lyapunov stable or Lyapunov asymptotically stable , which is exactly the same as we define to be stable solutions.
Examples of finding Lyapunov functions
  • Quadratic

    The function

    \begin{equation*} V(x, y) = ax^2 + bxy + cy^2 \end{equation*}

    is positive definite if and only if

    \begin{equation*} a > 0 \quad \text{and} \quad 4ac - b^2 > 0 \end{equation*}

    and is negative definite if and only if

    \begin{equation*} a < 0 \quad \text{and} \quad 4 ac - b^2 > 0 \end{equation*}
    • Example problem

      Show that the critical point $(0, 0)$ of the autonomous system

      \begin{equation*} \frac{dx}{dt} = - x -xy^2, \quad \frac{dy}{dt} = - y - x^2 y \end{equation*}

      is asymptotically stable.

      We try to construct a Liapunov function of the form

      \begin{equation*} V(x, y) = ax^2 + bxy + c y^2 \end{equation*}

      then

      \begin{equation*} V_x(x, y) = 2ax + by, \quad V_y(x, y) = 2cy + bx \end{equation*}

      thus,

      \begin{equation*} \begin{split} \dot{V} &= \frac{dV}{dt} = \frac{dV}{dx} \frac{dx}{dt} + \frac{dV}{dy} \frac{dy}{dt} \\ &= \big( 2ax + by \big) \big( - x - xy^2 \big) + \big( 2cy + bx \big) \big( -y -x^2 y \big) \\ &= - \Big( 2a \big( x^2 + x^2 y \big) + b \big( 2xy + xy^3 + x^3 y \big) + 2c \big( y^2 + x^2 y^2 \big) \Big) \end{split} \end{equation*}

      We observe that if we choose $b = 0$, and $a$ and $c$ to be positive numbers, then $\dot{V}$ is negative-definite and $V$ is positive-definite. Hence, the critical point $(0, 0)$ is asymptotically stable.

Partial Differential Equations

Consider the differential equation

\begin{equation*} y'' + p(x) y' + q(x) y = g(x) \end{equation*}

with the boundary conditions

\begin{equation*} y(\alpha) = y_0, \quad y(\beta) = y_1 \end{equation*}

We call this a two-point boundary value problem.

This is in contrast to what we're used to, which is initial value problems, i.e. where the restrictions are on the initial value of the differential equation, rather than the boundaries of the differential equations.

Eigenvalues and eigenfunctions

Consider the problem consisting of the differential equation

\begin{equation*} y'' + \lambda y = 0 \end{equation*}

together with the boundary conditions

\begin{equation*} y(0) = 0, \quad y(\pi) = 0 \end{equation*}

By extension of terminology from linear algebra, we call each nontrivial (non-zero) constant $\lambda$ an eigenvalue and the corresponding nontrivial (not everywhere zero) solution $y$ an eigenfunction.

Specific functions

Heat equation

Models heat distribution in a row of length $L$.

\begin{equation*} \alpha^2 u_{xx} = u_t \end{equation*}

with boundary conditions:

\begin{equation*} u(0, t) = 0, \quad u(L, t) = 0 \end{equation*}

and initial conditions:

\begin{equation*} u(x, 0) = f(x), \quad 0 \le x \le L \end{equation*}
Wave equation

Models vertical displacement $u(x, t)$ wrt. horizontal position $x$ and time $t$.

\begin{equation*} a^2 u_{xx} = u_{tt} \end{equation*}

where $a^2 = T / \rho$, $T$ being the tension in the string, and $\rho$ being the mass per unit length of the string material.

Reasonable to have the boundary conditions:

\begin{equation*} u(0, t) = 0, \quad u(L, t) = 0, \quad t \ge 0 \end{equation*}

i.e. the ends of the string are fixed.

And the initial conditions:

\begin{equation*} u(x, 0) = f(x), \quad u_t(x, 0) = g(x), \quad 0 \le x \le L \end{equation*}

i.e. we have some initial displacement $f(t)$ and initial (vertical) velocity $g(t)$. To keep our boundary condtions wrt. $x$ specified above consistent:

\begin{equation*} f(0) = f(L) = 0, \quad g(0) = g(L) = 0 \end{equation*}
Laplace equation
\begin{equation*} u_{xx} + u_{yy} = 0 \end{equation*}

or

\begin{equation*} u_{xx} + u_{yy} + u_{zz} = 0 \end{equation*}

Since we're dealing with multi-dimensional space, we have a couple of different ways to specify the boundary conditions:

  • Dirichlet problem : the boundary of the surface takes on specific values, i.e. we have a function $f(x, y)$ which specifies the values on the "edges" of the surface
  • Neumann problem : the values of the normal derivative are prescribed on the boundary

We don't have any initial conditions in this case, as there's no time-dependence.

  • Laplace's equation in cylindrical coordinates

    Let

    \begin{equation*} x = \rho \cos \varphi, \quad y = \rho \sin \varphi, \quad z = z \end{equation*}

    Laplace's equation becomes:

    \begin{equation*} \frac{1}{\rho} \frac{\partial}{\partial \rho} \bigg( \rho \frac{\partial \psi}{\partial \rho} \bigg) + \frac{1}{\rho^2} \frac{\partial^2 \psi}{\partial \psi^2} + \frac{\partial^2 \psi}{\partial z^2} = 0 \end{equation*}

    Consider BCs:

    \begin{equation*} \psi = 0 \text{ for } \rho = 1, \quad \psi = 0 \text{ for } z = 0, \quad \psi = \Psi(\rho, \varphi) \text{ for } z = 1 \end{equation*}

    Using separation of variables: $\psi(\rho, \varphi, z) = R(\rho) \varphi(\varphi)Z(z)$

    \begin{equation*} \frac{1}{R \rho} \frac{d}{d \rho} \bigg( \rho \frac{d R}{d \rho} \bigg) + \frac{1}{\rho^2 \phi} \frac{d^2 \phi}{d \varphi^2} + \frac{1}{Z} \frac{d^2 Z}{dz^2} = 0 \end{equation*}

    we can rewrite as:

    \begin{equation*} \begin{split} \frac{d^2 Z }{dz^2 } = \chi^2 Z &\quad \frac{d^2 \phi}{d \varphi^2} = - m^2 \phi \\ \frac{d^2 R}{d \rho^2} + \frac{1}{\rho} \frac{dR}{d \rho} & + \bigg( \chi^2 - \frac{m^2}{\rho^2} \bigg) R = 0 \end{split} \end{equation*}

    Using $\varphi(z = 0) = 0$, $Z(0) = 0$, hence

    \begin{equation*} \begin{split} \frac{d^2 Z}{dz^2} = \chi^2 Z &\quad \implies \quad Z(z) = a \sinh(\chi z) \\ \frac{d^2 \phi}{d \varphi^2} = - m^2 \phi &\quad \implies \quad \phi(\varphi) = f \cos m \varphi + g \sin m \varphi \end{split} \end{equation*}

    Thus, if $m \in \mathbb{Z}$, solutions are periodic.

    The radial equation can be written in the SL-form

    \begin{equation*} - \big( \rho R' \big)' + \frac{m^2}{\rho} R = \chi^2 \rho R \end{equation*}

    Thus,

    • $p(\rho) = r(\rho) = \rho$: vanish at the origin $\rho = 0$
    • $q(\rho) = \frac{m^2}{\rho}$: unbounded as $\rho \to 0$

    Finally, making the change of variables $x = \chi \rho$ amd write $R(\rho) = y(x)$, we have

    \begin{equation*} y'' + \frac{1}{x}y' + \Bigg( 1 - \frac{m^2}{x^2} \Bigg) y = 0 \end{equation*}

    Which is the Bessel equation, and we have the general solution:

    \begin{equation*} R_m(\rho) = c_1 J_m(\chi \rho) + c_2 Y_m(\chi \rho) \end{equation*}

    Imposing the boundary conditions:

    • $R_m(1) = 0$
    • $R_m(\rho)$ as $\rho \to 0$ needs to be bounded
    • $J_0(0) = 1$ and $J_m(0) = 0$ for $m \ge 1$
    • $Y_m(\rho) \to - \infty$ as $\rho \to 0$ (due to log)

    Hence, we require

    \begin{equation*} c_2 = 0 \quad \text{and} \quad J_m(\chi) = 0 \end{equation*}

    Plotting these Bessel functions, we conclude there exists a countable infinite number of eigenvalues.

    We now superpose the solutions:

    \begin{equation*} \psi_{mn} = \big( f_{mn} \cos (m \varphi) + g_{mn} \sin(m \varphi) \big) J_m(\chi_{mn} \rho) \sinh(\chi_{mn} z) \end{equation*}

    to write the general solution as

    \begin{equation*} \psi(\rho, \varphi, z) = \sum_{m = 0}^{\infty} \sum_{n = 0}^{\infty} \psi_{mn}(\rho, \varphi, z) \end{equation*}

    The constants $f_{mn}$ and $g_{mn}$ are found from the remaining BC,

    \begin{equation*} \Psi(\rho, \varphi) = \sum_{m=0}^{\infty} \sum_{n=0}^{\infty} \psi_{mn}(\rho, \varphi, 1) \end{equation*}

    by projection on $\cos(m \varphi) J_m(\chi_{mn} \rho)$ and $\sin (m \varphi) J_m(\chi_{mn} \rho)$.

    Orthogonality: the Besseul functions $R_{mn}(\rho) = J_n(\chi_{mn} \rho)$ satisfy

    \begin{equation*} L[R_{mn}] = - \big( \rho R_{mn}' \big)' + \frac{m^2}{\rho} R_{mn} = \rho \xi^2 R_{mn} \end{equation*}

    Which has the Sturm-Liouville form, with

    \begin{equation*} \langle L[u], v \rangle = \langle u, L[v] \rangle \end{equation*}

    provided that

    \begin{equation*} 0 = p(x) [u'v - u v']_0^1 \end{equation*}

    The functions $R_{mn}$ satisfy the above at $\rho = 1$, where the contribution at $\rho = 1$ vanishes, and at $\rho = 0$ we have

    \begin{equation*} \lim_{\varepsilon \to 0} p(\varepsilon) [u'(\varepsilon)v(\varepsilon) - u(\varepsilon)v'(\varepsilon)] = 0 \end{equation*}

    since $p(\rho) = \rho$ and $u, v, u'$ and $v'$ are bounded.

    We conclude

    \begin{equation*} \int_{0}^{1} \rho J_{m}(\chi_{mn} \rho) J_{m}(\chi_{mn'} \rho) \ d \rho = 0 \end{equation*}

    for $n \ne n$. We can therefore identify the constants $f_{mn}$ and $g_{mn}$ by projection:

    \begin{equation*} \begin{split} f_{mn} &\prodto \int_{0}^{1} \int_{- \pi}^{\pi} \Psi(\rho, \varphi) \cos(m \varphi) J_m(\chi_{mn} \rho) \rho \ d \rho d \varphi \\ g_{mn} &\prodto \int_{0}^{1} \int_{- \pi}^{\pi} \Psi(\rho, \varphi) \sin(m \varphi) J_m(\chi_{mn} \rho) \rho \ d \rho d \varphi \end{split} \end{equation*}

Boundary Value Problems and Sturm-Liouville Theory

Notation

  • $L[y] = - [p(x) y']' + q(x) y$
  • $\lambda_1 < \lambda_2 < \dots < \lambda_n < \dots$ are the ordered eigenvalues
  • $\phi_1, \phi_2, \dots, \phi_n, \dots$ are the corresponding normalized eigenfunctions
  • $f(x+) = \underset{x \to x^+}{\lim} f(x)$ and equivalent for $f(x-)$

Sturm-Liouville BVP

Equation of the form:

\begin{equation*} [p(x) y']' - q(x) y + \lambda r(x) y = 0 \end{equation*}

OR equivalently

\begin{equation*} L[y] = \lambda r(x) y \end{equation*}

with boundary conditions:

\begin{equation*} \alpha_1 y(0) + \alpha_2 y'(0) = 0, \quad \beta_1 y(1) + \beta_2 y'(1) = 0 \end{equation*}

where we the boundary value problem to be regular, i.e.:

  • $p, p', q$ and $r$ are continuous on the interval $[0, 1]$
  • $p(x) > 0$ and $r(x) > 0$ for all $x \in [0, 1]$

and the boundary conditions to be separated, i.e.:

  • each involves only on the of the boundary points
  • these are the most general boundary conditions you can have for a 2nd order differential equation
Lagrange's Identity

Let $u$ and $v$ be functions having continous second derivatives on the interval $x \in [0, 1]$, then

\begin{equation*} \int_0^1 L[u] \ v \ dx = \int_0^1 [- (pu')' v + quv ] \ dx \end{equation*}

where $L[y]$ is given by

\begin{equation*} L[y] = - [p(x) y']' + q(x) y \end{equation*}

In the case of a Sturm-Liouville problem we have observe that the Lagrange's identity gives us

\begin{equation*} \int_0^1 L[u] v - u L[v] \ dx = - p(x) [u'(x) v(x) - u(x) v'(x)] \Big|_0^1 \end{equation*}

Which we can expand to

\begin{equation*} - p(x) [u'(x) v(x) - u(x) v'(x)] \Big|_0^1 = - p(1) [u'(1) v(1) - u(1) v'(1)] + p(0) [u'(0)v(0) - u(0)v'(0)] \end{equation*}

Now, using the boundary conditions from the Sturm-Liouville problem, and assuming that $\alpha_2 \ne 0$ and $\beta_2 \ne 0$, we get

\begin{equation*} \begin{split} - p(x) [u'(x) v(x) - u(x) v'(x)] \Big|_0^1 &= - p(1) \Bigg[\frac{\beta_1}{\beta_2} u(1) v(1) - u(1) \frac{\beta_1}{\beta_2} v(1) \Bigg] + \Bigg[\frac{\alpha_1}{\alpha_2} u(1) v(1) - u(1) \frac{\alpha_1}{\alpha_2} v(1) \Bigg] \\ &= 0 \end{split} \end{equation*}

And if either $\alpha_2$ or $\beta_2$ are zero, $u(1) = v(1) = 0$ or $u(0) = v(0) = 0$ and the statement still holds.

I.e. the Lagrange's identity under the Sturm-Liouville boundary conditions equals zero.

If $u, v$ are solutions to a boundary value problem of the form def:sturm-lioville-problem, then

\begin{equation*} \int_0^1 L[u] v - u L[v] \ dx = 0 \end{equation*}

or in the form of an inner product

\begin{equation*} \langle L[u], v \rangle - \langle u, L[v] \rangle = 0 \end{equation*}

If a singular boundary value problem of the form def:sturm-lioville-problem satisfies thm:lagranges-identity-sturm-liouville-boundary-conditions then we say the problem is self-adjoint. More specifically,

\begin{equation*} L[y] = \lambda r(x) y \end{equation*}

for an n-th order operator

\begin{equation*} L[y] = p_n(x) \frac{d^n y}{dx^n} + \dots + p_1(x) \frac{dy}{dx} + p_0(x) y \end{equation*}

subject to $n$ linear homogenous boundary conditions at the endpoints is self-adjoint provided that

\begin{equation*} \langle L[u], v \rangle - \langle u, L[v] \rangle = 0 \end{equation*}

E.g. for 4th order we can have

\begin{equation*} L[y] = \big[ p(x) y'' \big]'' - [q(x) y']' + s(x) y \end{equation*}

plus suitable BCs.

Most results from the 2nd order problems extends to the n-th order problems.

Some theorems

All the eigenvalues of the Sturm-Liouville problem are real.

If $\phi_m$ and $\phi_n$ are two eigenfunctions of the Sturm-Lioville problem corresponding to the eigevalues $\lambda_m$ and $\lambda_n$, respectively, and if $\lambda_m \ne \lambda_n$, then

\begin{equation*} \int_0^1 r(x) \phi_m(x) \phi_n(x) \ dx = 0 \end{equation*}

That is, the eigenfunctions $\phi_n, \phi_m$ are *orthogonal to each other wrt. the weight function $r(x)$.

We note that $\phi_m$ and $\phi_n$, with $\lambda_m \ne \lambda_n$, satisfy the differential equations

\begin{equation*} L[\phi_m] = \lambda_m r \phi_m \end{equation*}

and

\begin{equation*} L[\phi_n] = \lambda_n r \phi_n \end{equation*}

respectively. If we let $u = \phi_m$ and $v = \phi_n$, and substitute $L[u]$ and $L[v]$ into Lagrange's Identity with Sturm-Liouville boundary conditions, we get

\begin{equation*} \int_0^1 \lambda_m r(x) \phi_m(x) \phi_n(x) - \lambda_n r(x) \phi_n(x) \phi_m(x) \ dx = (\lambda_m - \lambda_n) \int_0^1 r(x) \phi_m(x) \phi_n(x) \ dx = 0 \end{equation*}

which implies that $\langle \phi_m, \phi_n \rangle_r$ where $\langle \cdot, \cdot \rangle_r$ represents the inner-product wrt. $r(x)$.

The above theorem has further consequences that, if some function $f$ satisfies is continuous on $x \in [0, 1]$, then we can expand $f$ as a linear combination of the eigenfunctions of the Sturm-Liouville equation!

Let $\phi_1, \phi_2, \dots, \phi_n, \dots$ be the normalized eigenfunctions of the Sturm-Liouville problem.

Let $f$ and $f'$ be piecewise continuous on $x \in [0, 1]$. Then the series

\begin{equation*} \sum_{n=1}^{\infty} c_m \phi_m(x) \end{equation*}

whose coefficients $c_m$ are given by

\begin{equation*} c_m = \langle \phi_m, f \rangle_r = \int_0^1 \lambda \phi_m(x) r(x) f(x) \ dx \end{equation*}

converges to $[f(x+) + f(x-)] / 2$ at each point in the open interval $x \in (0, 1)$.

The eigenvalues of the Sturm-Liouville problem are all simple; that is, to each eigenvalue there corresponds only one linearly independent eigenfunction.

Further, the eigenvalues form an infinite sequence and can be ordered according to increasing magnitude so that

\begin{equation*} \lambda_1 < \lambda_2 < \dots < \lambda_n \end{equation*}

Moreover, $\lambda_n \to \infty$ as $n \to \infty$.

Non-homogenous Sturm-Liouville BVP

"Derivation"

Consider the BVP consisting of the nonhomogenous differential equation

\begin{equation*} L[y] = - [p(x) y']' + q(x) y = \mu r(x) y + f(x) \end{equation*}

where $\mu$ is a given constant and $f$ is a given function on $x \in [0, 1]$, and the boundary conditions are as in homogeonous Sturm-Lioville.

To find a solution to this non-homogenous case we're going to start by obtaining the solution for the corresponding homogenous system, i.e.

\begin{equation*} L[y] = \lambda r(x) y \end{equation*}

where we let $\lambda_1 < \lambda_2 < \dots < \lambda_n < \dots$ be the eigenvalues and $\phi_1, \phi_2, \dots, \phi_n, \dots$ be the eigenfunctions of this differential equation. Suppose

\begin{equation*} y = \phi(x) = \sum_{n=1}^{\infty} b_n \phi_n(x) \end{equation*}

i.e. we write the solution as a linear combination of the eigenfunctions.

In the homogenous case we would now obtain the coefficients $b_n$ by

\begin{equation*} b_n = \langle \phi_n, \phi \rangle_r = \int_0^1 \phi_n(x) r(x) \phi(x) \ dx \end{equation*}

which we're allowed to do as a result of the orthogonality of the eigenfunctions wrt. $r(x)$.

The problem here is that we actually don't know the eigenfunctions $\phi_n$ yet, hence we need a different approach.

We now notice that $\phi$ always satisfies the boundary conditions of the problem, since each $\phi_n$ does! Therefore we only need to deduce $b_n$ such that the differential equation is also satisifed. We start by substituing our expansion of $\phi$ into the LHS of the differential equation

\begin{equation*} L[\phi] = L \Bigg[ \sum_{n=1}^{\infty} b_n \phi_n(x) \Bigg] = \sum_{n=1}^{\infty} b_n L[\phi_n] = \sum_{n=1}^{\infty} b_n \lambda_n \phi_n(x) r(x) \end{equation*}

since $L[\phi_n] = \lambda_n r \phi_n$ from the homogenous SL-problem, where we have assumed that we interchange the operations of summations and differentiation.

Observing that the weight function $r(x)$ occurs in all terms except $f(x)$. We therefore decide to rewrite the nonhomogenous term $f(x)$ as $r(x) [f(x) / r(x)]$, i.e.

\begin{equation*} L[\phi] = r(x) \phi(x) + r(x) \frac{f(x)}{r(x)} \end{equation*}

If the function $f / r$ satisfies the conditions in thm:boyce-11.2.4, we can expand it in the eigenfunctions:

\begin{equation*} \frac{f(x)}{r(x)} = \sum_{n=1}^{\infty} c_n \phi_n(x) \end{equation*}

where

\begin{equation*} c_n = \int_0^1 r(x) \frac{f(x)}{r(x)} \phi_n(x) \ dx = \int_0^1 f(x) \phi_n(x) \ dx, \quad n = 1, 2, \dots \end{equation*}

Now, substituting this back into our differential equation we get

\begin{equation*} \sum_{n=1}^{\infty} b_n \lambda_n \phi_n(x) r(x) = \mu r(x) \Bigg( \sum_{n=1}^{\infty} b_n \phi_n(x) \Bigg) + r(x) \sum_{n=1}^{\infty} c_n \phi_n(x) \end{equation*}

Dividing by $r(x)$, we get

\begin{equation*} \sum_{n=1}^{\infty} b_n \lambda_n \phi_n(x) = \mu \Bigg( \sum_{n=1}^{\infty} b_n \phi_n(x) \Bigg) + \sum_{n=1}^{\infty} c_n \phi_n(x) \end{equation*}

Collecting terms of the same $n$ we get

\begin{equation*} \sum_{n=1}^{\infty} \Big( b_n (\lambda_n - \mu) - c_n \Big) \varphi(x) = 0 \end{equation*}

Now, for this to be true for all $x$, we need each of the $n$ terms to equal zero. To make our life super-simple, we assume $\lambda_n \ne \mu$ for all $n$, then

\begin{equation*} b_n = \frac{c_n}{\lambda_n - \mu}, \quad n = 1, 2, \dots \end{equation*}

and thus,

\begin{equation*} y = \phi(x) = \sum_{n=1}^{\infty} \frac{c_n}{\lambda_n - \mu} \phi_n(x) \end{equation*}

And remember, we already have an expression for $c_n$ and know $\lambda_n$ from the corresponding homogeonous problem.

If $\lambda_m = \mu$ for some $m$ then we have two possible cases:

  • $\lambda_m = \mu \ne 0$ and thus there exists no solution of the form we just described
  • $\lambda_m = \mu = 0$ in which case $\int_0^1 f(x) \phi_m(x) \ dx = 0$, thus we can only solve the problem if $f$ is orthogonal to $\phi_m$; in this case we have an infinite number of solutions since the m-th coefficient can be arbitrary.
Summary
\begin{equation*} L[y] = \mu \ r(x) y + f(x) \end{equation*}

with boundary conditions:

\begin{equation*} \alpha_1 y(0) + \alpha_2 y'(0) = 0, \qquad \beta_1 y(1) + \beta_2 y'(1) = 0 \end{equation*}

Expanding $f = r \frac{f}{r} = \sum_{i=1}^{n} c_n \phi_n$, which means that we can rewrite the diff. eqn. as

\begin{equation*} \begin{split} L[\phi] &= \mu r \phi + \sum_{i=1}^{n} c_n \phi_n r \Big( \frac{f}{r} \Big) \\ L \Big[ \sum_{i=1}^{n} b_n \phi_n \Big] &= \end{split} \end{equation*}

We have the solution

\begin{equation*} y = \phi(x) = \sum_{n=1}^{\infty} \frac{c_n}{\lambda_n - \mu} \phi_n(x), \quad \lambda_n \ne \mu \end{equation*}

where $\lambda_n$ and $\phi_n(x)$ are the eigenvalues and eigenfunctions of the corresponding homogenous problem, and

\begin{equation*} c_n = \Big \langle \frac{f(x)}{r(x)}, \phi_n \Big \rangle_r = \int_0^1 r(x) \frac{f(x)}{r(x)} \phi_n(x) \ dx = \int_0^1 f(x) \phi_n(x) \ dx \end{equation*}

If $\lambda_m = \mu$ for some $m$ we have:

  • $\lambda_m = \mu \ne 0$ in which case there exist no solution of the form described above
  • $\lambda_m = \mu = 0$ i which case $\langle f / r, \phi_m \rangle_r = 0$; in this case we have an infinite number of solutions since the m-th coefficient can be arbitrary

Where we have made the following assumptions:

  • Can rewrite the nonhomogenous part as $f(x) = r(x) \ [ f(x) / r(x) ]$
  • Can expand $f(x) / r(x)$ using the eigenfunctions $\phi_m$ wrt. $r$, which requires $f$ and $f'$ to be continuous on the domain $x \in [0, 1]$

Inhomogenous BCs Sturm-Liouville BVP

Derivation (sort-of-ish)

Consider we have at our hands a Sturm-Liouville problem of the sort:

\begin{equation*} \partial_{xx}^2 u - \beta^2 u = \partial_{tt}^2 u, \qquad x \in [0, a], \quad t > 0 \end{equation*}

for any $a, \beta \in \mathbb{R}^+$, satisfying the boundary conditions

\begin{equation*} \begin{split} u(0, t) = 0 &\quad u(a, t) = 0, \quad t > 0 \\ u(x, 0) = f(x), &\quad \partial_t u(x, 0) = 0, \quad \forall x \in [0, a] \end{split} \end{equation*}

This is just a specific Sturm-Liouville problem we will use to motivate how to handle these inhomogenous boundary-conditions.

Suppose we've already obtained the solutions for the above SL-problem using separation of variables, and ended up with:

\begin{equation*} u_n(x, t) = X_n(x) T_n(t) \end{equation*}

as the eigenfunctions, with the general solution:

\begin{equation*} u(x, t) = \sum_{i=1}^{n} c_n u_n(x, t) \end{equation*}

where $c_n = \langle u_n, f \rangle$ such that we satisfy the $u(x, 0)$ BC given above.

Then, suddenly, the examinator desires you to solve the system for a slightly different set of BCs:

\begin{equation*} u(0, t) = T_1, \quad u(a, t) = T_2 \end{equation*}

What an arse, right?! Nonetheless, motivated by the potential of showing that you are not fooled by such simple trickeries, you assume a solution of the form:

\begin{equation*} w(x, t) = u(x, t) + v(x, t) \end{equation*}

where $u(x, t)$ is just as you found previously for the homogenous BCs.

Eigenfunctions (i.e. (countable) infinite number of orthogonal solutions)) arise only in the case of homogenous BCs, as we then still have the Lagrange's identity being satisifed. For inhomogenous BCs, it's not satisfied, and we're not anymore working with a Sturm-Liouville problem.

Nonetheless, we're still solving differential equations, and so we still have the principle of superposition available to work with.

Why would you do that? Well, setting up the new BCs:

\begin{equation*} \begin{split} w(0, t) = u(0, t) + v(0, t) = T_1 &\quad w(a, t) = u(a, t) + v(a, t) = T_2, \quad t > 0 \\ w(x, 0) = u(x, 0) + v(x, 0) = f(x), &\quad \partial_t w(x, 0) = \partial_t u(x, 0) + \partial_t v(x, 0) = 0, \quad \forall x \in [0, a] \end{split} \end{equation*}

Now, we can then quickly observe that we have some quite major simplifications:

\begin{equation*} \begin{split} u(0, t) &= 0 \quad \implies \quad v(0, t) = T_1 \\ u(a, t) &= 0 \quad \implies \quad v(a, t) = T_2 \end{split} \end{equation*}

If we then go on to use separation of variables for $v(x, t)$ too, we have

\begin{equation*} v(x, t) = Y(x) \tau (t) \end{equation*}

Substituting into the simplified BCs we just obtained:

\begin{equation*} v(0, t) = Y(0) \tau(t) = T_1, \quad v(a, t) = Y(a) \tau(t) = T_2 \end{equation*}

Here it becomes quite apparent that this can only work if $\tau(t) = \text{const}$, and if we simply include this constant factor into our $Y(x)$, we're left with the satisfactory simple expressions:

\begin{equation*} v(0, t) = Y(0) = T_1, \quad v(a, t) = Y(a) = T_2 \end{equation*}

This is neat and all, but we're not quuite ready to throw gang-signs in front of the examinator in celebration quite yet. Our expression for the additional $v(x, t)$ has now been reduced to

\begin{equation*} v(x, t) = Y(x) \end{equation*}

Substituting this into the differential equation (as we still of course have to satisfy this), we get

\begin{equation*} Y'' - \beta^2 Y = 0 \end{equation*}

where the t-dependent factor has vanished due to our previous reasoning (magic!). Recalling that $\beta > 0$, the general solution is simply

\begin{equation*} Y(x) = E \cosh (\beta x) + F \sinh(\beta x) \end{equation*}

Substituting into the BCs from before:

\begin{equation*} \begin{split} Y(0) &= T_1 \quad \implies \quad E = T_1 \\ Y(a) = T_2 \quad \implies \quad T_1 \cosh (\beta a) + F \sinh(\beta a) = T_2 \end{split} \end{equation*}

where the last BC $Y(a) = T_2$ gives us

\begin{equation*} F = \frac{T_2 - T_1 \cosh(\beta a)}{\sinh(\beta a)} \end{equation*}

thus,

\begin{equation*} Y(x) = T_1 \cosh(\beta x) + \frac{T_2 - T_1 \cosh(\beta a)}{\sinh (\beta a)} \sinh(\beta x) \end{equation*}

Great! We still have to satisfy the initial-values, i.e. the BCs for $t = 0$. We observe that they have now become:

\begin{equation*} \begin{split} w(0, t) &= u(0, t) + v(0, t) = f(x) \quad \implies \quad u(0, t) = f(x) - Y(x) \\ \partial_t w(0, t) &= \partial_t u(0, t) + \partial_t v(0, t) = \partial_t u(0, t) = 0 \end{split} \end{equation*}

where the last t-dependent BC stays the same due to $v(x, t) = Y(x)$ being independent of $t$. For the first BC, the implication arises from the fact that we cannot alter $Y(x)$ any further to accomodate the change to the complete solution, hence we alter $u(x, t)$. With this alteration, we end up with the complete and final solution to the inhomogenous boundary-condition problem

\begin{equation*} w(x, t) = Y(x) + \sum_{n=1}^{\infty} d_n u_n(x, t) \end{equation*}

where

\begin{equation*} d_n = \langle u_n, f(x) - Y(x) \rangle = \frac{\int_{0}^{a} u_n^*(x) \Big( f(x) - Y(x) \Big) \ dx}{\int_{0}^{a} u_n^*(x) u_n(x) \ dx} \end{equation*}

At this point it's fine to throw gang-signs and walk out.

Observe that $Y(x)$ is kept outside of the sum. It's a tiny tid-bit that might be forgotten in all of this mess: we're adding a function to the general solution to the "complete" PDE, that is

\begin{equation*} w(x, t) = u(x, t) + v(x, t) = u(x, t) + Y(x) \end{equation*}

NOT something like this $w_n(x, t) = u_n(x, t) + Y(x)$.

I sort of did that right away.. But quickly realized I was being, uhmm, not-so-clever. Though I guess we could actually do it if we knew $Y(x)$ to be square-integrable! Buuut..yeah, I was still being not-so-clever.

Example

Suppose we we're presented with a modified wave equation of the following form:

\begin{equation*} \partial_{xx}^2 u - \beta^2 u = \partial_{tt}^2 u, \qquad x \in [0, a], \quad t > 0 \end{equation*}

for any $a, \beta \in \mathbb{R}^+$, satisfying the boundary conditions

\begin{equation*} \begin{split} u(0, t) = 0 &\quad u(a, t) = 0, \quad t > 0 \\ u(x, 0) = f(x), &\quad \partial_t u(x, 0) = 0, \quad \forall x \in [0, a] \end{split} \end{equation*}

and we found the general solution to be

\begin{equation*} u(x, t) = \sum_{n=1}^{\infty} c_n \sin ( \frac{\pi n}{a} x ) \cos (\alpha_n t) \ dt \end{equation*}

where $c_n$ is as given above.

Now, one might wanted, what would the solution be if we suddenly decided on a set of non-homogenous boundary conditions :

\begin{equation*} u(0, t) = T_1, \qquad u(a, t) = T_2, \qquad T_1, T_2 \in \mathbb{R}^+ \end{equation*}

To deal with non-homogenous boundary conditions, we look for a time independent solution $v(x)$ solving the boundary problem

\begin{equation*} v''(x) - \beta^2 v(x) = 0, \qquad v(0) = T_1, \qquad v(a) = T_2 \end{equation*}

Once $v(x)$ is known, we determine the solution to the modified wave equation using

\begin{equation*} u(x, t) = v(x) + w(x, t) \end{equation*}

where $w(x, t)$ satisfies the same modified equation with different initial conditions, but homogenous boundary conditions. Indeed,

\begin{equation*} \begin{split} w(0, t) &= u(0, t) - v(0) = 0 \\ w(L, t) &= u(a, t) - v(a) = 0 \\ w(x, 0) &= f(x) - v(x) \end{split} \end{equation*}

To determine $v(x)$, we solve the second order ODE with constant coefficients. Since $\beta > 0$, its general solution is given by

\begin{equation*} v(x) = a \cosh \beta x + b \sinh \beta x \end{equation*}

We fix the arbitrary constants using the given boundary conditions

\begin{equation*} \begin{split} v(0) = T_1 \quad &\implies \quad a = T_1, \\ v(a) = T_2 \quad &\implies \quad b = \frac{T_2 - T_1 \cosh \beta a}{\sinh \beta a} \end{split} \end{equation*}

Thus, the general solution is given by

\begin{equation*} v(x) = T_1 \cosh \beta x + \frac{T_2 - T_1 \cosh \beta a}{\sinh \beta a} \sinh \beta x \end{equation*}

By construction, the remaining $w(x, t)$ is as in the previous section, but with the coefficients $C_n$ satisfying

\begin{equation*} c_n = \frac{2}{a} \int_{0}^{a} \big( f(x) - v(x) \big) \sin \frac{\pi n }{a} x \ dx \end{equation*}

Thus, the very final solution is given by

\begin{equation*} \begin{split} u(x, t) &= v(x) + w(x, t) \\ &= \Bigg( T_1 \cosh \beta x + \frac{T_2 - T_1 \cosh \beta a}{\sinh \beta a} \sinh \beta x \Bigg) + \Bigg( \sum_{n=1}^{\infty} c_n \sin ( \frac{\pi n}{a} x ) \cos (\alpha_n t) \Bigg) \end{split} \end{equation*}

with $c_n$ as given above.

Singular Sturm-Liouville Boundary Value Problems

We use the term singluar Sturm-Liouville problem to refer to a certain class of boundary value problems for the differential equation

\begin{equation*} L[y] = \lambda r(x) y, \quad 0 < x < 1 \end{equation*}

in which the functions $p, q$ and $r$ satisfy the conditions (same as in the "regular" Sturm-Liouville problem) on the open interval $0 < x < 1$, but at least one of the functions fails to satisfy them at one or both of the boundary points.

Discussion

Here we're curious about the following questions:

  1. What type of boundary conditions can be allowed in a singular Sturm-Liouville problem?
  2. What's the same as in the regular Sturm-Liouville problem?
    • Are the eigenvalues real?
    • Are the eigenfunctions orthogonal?
    • Can a given function be expanded as a series of eigenfunctions?

These questions are answered by studying Lagrange's identity again.

To be concrete we assume $x = 0$ is a singular point while $x = 1$ is not.

Since the boundary value problem is singular at $x = 0$ we choose $\varepsilon > 0$ and consider the improper integral

\begin{equation*} \int_{\varepsilon}^1 \{ L[u] v - u L[v] \} \ dx = - p(x) [ u'(x) v(x) - u(x) v'(x) ] \Big|_{\varepsilon}^{1} \end{equation*}

If we assume the boundary conditions at $x = 1$ are still satisfied, then we end up with

\begin{equation*} \int_{\varepsilon}^1 \{ L[u] v - u L[v] \} \ dx = p(\varepsilon) [ u'(\varepsilon) v(\varepsilon) - u(\varepsilon) v'(\varepsilon)] \end{equation*}

Taking the limit as $\varepsilon \to 0$ :

\begin{equation*} \int_0^1 \{ L[u] v - u L[v] \} \ dx = \underset{\varepsilon \to 0}{\lim} \ p(\varepsilon) [ u'(\varepsilon) v(\varepsilon) - u(\varepsilon) v'(\varepsilon)] \end{equation*}

Therefore, if we have

\begin{equation*} \underset{\varepsilon \to 0}{\lim} \ p(\varepsilon) [ u'(\varepsilon) v(\varepsilon) - u(\varepsilon) v'(\varepsilon)] = 0 \end{equation*}

we have the same properties as we did for the regular Sturm-Liouville problem!

General

In fact, it turns out that the Sturm-Liouville operator

\begin{equation*} L[y] = \frac{1}{w(x)} \Big( - [p(x) y'(x)]' + q(x) y(x) \Big) \end{equation*}

on the space of function satisfying the boundary conditions of the singular Sturm-Liouville problem $H$, is a self-adjoint operator, i.e. it satisfies the Lagrange's identity on this space!

And this as we have seen indications for above a sufficient property for us to construct a space of solutions to the differential equation with these eigenfunctions as a basis.

A bit more information

These lecture notes provide a bit more general approach to the case of singular Sturm-Liouville problems: http://www.iitg.ernet.in/physics/fac/charu/courses/ph402/SturmLiouville.pdf.

Frobenius method

Frobenius method refers to the method where we assume the solution of a differential equation to be analytic, i.e. we can expand it as a power series:

\begin{equation*} y(x) = \sum_{n=0}^{\infty} a_n x^n \end{equation*}

Substituting this into the differential equation, we can quite often derive recurrence-relations by grouping powers of $x$ and solving for $a_n$.

Honours Differential Equations

Equations / Theorems

Reduction of order

Go-to way

If we have some repeated roots of the characteristic equation $r_1 = r_2$ , then the general solution is

\begin{equation*} y = c_1 e^{r_1 t} + c_2 t e^{r_1 t} \end{equation*}

where we've taken the linear combination of the "original" solution

\begin{equation*} y_1 = c_1 e^{r_1 t} \end{equation*}

and the one obtained from reduction of order

\begin{equation*} y_2 = c_2 t e^{r_1 t} \end{equation*}
General

If we know a solution $y_1$ to an ODE, we can reduce the order by 1, by assuming another solution $y_2$ of the form

\begin{equation*} y_2(x) = y_1(x) u(x) \end{equation*}

where $u(x)$ is some arbitrary function which we can find from the linear system obtained from $y(x)$, $y_2'(x)$ and $y_2''(x)$. Solving this system gives us

\begin{equation*} u(x) = ax + b \end{equation*}

i.e. we multiply our first solution with a first-order polynomial to obtain a second solution.

Integrating factor

Assume $y = e^{rx}$ to be a solution, then in a 2nd order homogeneous ODE we get the

\begin{equation*} (r^2 + p r + q) e^{rx} = 0 \end{equation*}

Which means we can obtain a solution by simply solving the quadratic above.

This can also be performed for higher order homogeneous ODEs.

Repeated roots

What if we have a root of algebraic multiplicity greater than one?

If the algebraic multiplicity is 2, then we can use reduction of order and multiply the first solution for this root with the $u(x)$.

Factorization of higher order polynomials (Long division of polynomials)

Good website with examples

Suppose we want to compute the following

\begin{equation*} \frac{3x^3 - 5x^2 + 10x - 3}{3x + 1} \end{equation*}
  1. Divide the first highest order factor of the polynomial by the highest order factor of the divisor, i.e. divide $3x^3$ by $3x$, which gives $x^2$
  2. Multiply the $x^2$ from the above through by the divisor $3x + 1$, thus giving us $3x^3 + x^2$
  3. We subtract this from the corresponding terms of the polynomial, i.e. $3x^3 - 5x^2 - (3x^3 + x^2) = -6x^2$
  4. Divide this remainder by the highest order term in of the divisor again, and repeating this process until we cannot divide by the highest order term of the divisor.

Existence and uniqueness theorem

Consider the IVP

\begin{equation*} y'' + p(t) y' + q(t) y = g(t), \quad y(t_0) = y_0, \quad y'(t_0) = y'_0 \end{equation*}

where $p$ , $q$, and $g$ are continuous on an open interval $I$ that contains the point $t_o$. There is exactly one solution $y = \phi(t)$ of this problem, and the solution exists throughout the interval $I$.

Exact differential equation

Let the functions $M, N, M_y$ and $N_x$, where subscripts denote the partial derivatives, be continuous in the rectangular region $R: \alpha < x < \beta, \gamma < y < \delta$. Then

\begin{equation*} M(x, y) + N(x, y) \frac{dy}{dx} = 0 \end{equation*}

is an exact differential equation in $R$ if and only if

\begin{equation*} M_y(x, y) = N_x(x, y) \end{equation*}

at each point of $R$. That is, there exists a function $\psi$ such that

\begin{equation*} \psi_x(x, y) = M(x, y), \quad \psi_y(x, y) = N(x, y) \end{equation*}

if and only if $M$ and $N$ satisfy the equality above above.

Variation of Parameters

Suppose we have the n-th order linear differential equation

\begin{equation*} L[y] = y^{(n)} + p_1(t) y^{(n - 1)} + \dots + p_{n - 1}(t) y' + p_n(t)y = g(t) \end{equation*}

Suppose we have found the solutions to the corresponding homogenous diff. eqn.

\begin{equation*} y_h(t) = c_1 y_1(t) + c_2 y_2(t) + \dots + c_n y_n(t) \end{equation*}

With the method of variation of parameters we seek a particular solution of the form

\begin{equation*} y_p(t) = u_1(t) y_1(t) + u_2(t) y_2(t) + \dots + u_n(t) y_n(t) \end{equation*}

Since we have $n$ functions $u_i(t)$ to determine we have to specify $n$ conditions.

One of these conditions is cleary that we need to satisfy the non-homongenous diff. eqn. above. Then the $n - 1$ other conditions are chosen to make the computations as simple as possible.

Taking the first partial derivative wrt. $t$ of $y_p$ we get (using the product rule)

\begin{equation*} y_p' = (u_1' y_1 + \dots + u_n' y_n) + (u_1 y_1' + \dots + u_n y_n') \end{equation*}

We can hardly expect it to be simpler to determine $y_p$ if we have to solve diff. eqns. of higher order than what we started out with; hence we try to surpress the terms that lead to higher derivatives of $u_1, \dots, u_n$ by imposing the following condition

\begin{equation*} u_1' y_1 + \dots + u_n' y_n = 0 \end{equation*}

which we can do since we're just looking for some arbitrary functions $u_i$. The expression for $y_p'$ then reduces to

\begin{equation*} y_p' = u_1 y_1' + \dots + u_n y_n' \end{equation*}

Continuing this process for the derivatives $y_p'', \dots, y_p^{(n - 1)}$ we obtain our $n - 1$ condtions:

\begin{equation*} u_1' y_1^{(m)} + \dots + u_n' y_n^{(n)} = 0, \quad m = 1, 2, \dots, n - 2 \end{equation*}

giving us the expression for the m-th derivative of $y_p$ to be

\begin{equation*} y_p^{(m)} = u_1 y_1^{(m)} + \dots + u_n y_n^{(m)}, \quad m = 2, 3, \dots, n - 1 \end{equation*}

Finally, imposing that $y_p^{(n)}$ has to satisfy the original non-homogenous diff. eqn. we take the derivative of $y_p^{(n - 1)}$ and substitute back into the equation. Doing this, and grouping terms involving each of $y_i$ together with their derivatives, most of the terms drop out due to $y_i$ being a solution to the homogenous diff. eqn., yielding

\begin{equation*} u_1' y_1 + \dots + u_n' y_n = g \end{equation*}

Together with the previous $n - 1$ conditons we end up with a system of linear equations

\begin{equation*} \begin{cases} y_1 u_1' + \dots y_n u_n' &= 0 \\ y_1' u_1' + \dots y_n' u_n' &= 0 \\ & \vdots \\ y_1^{(n - 1)} u_1' + \dots y_n^{(n - 1)} u_n' &= g \\ \end{cases} \end{equation*}

(note the $g$ at the end!).

The sufficient condition for the existence of a solution of the system of equations is that the determinant of coefficients is nonzero for each value of $t$. However, this is guaranteed since $\{y_i\}$ form a fundamental set of solutions for the homogenous eqn.

In fact, using Cramers rule we can write the solution of the system of equations in the form

\begin{equation*} u_m'(t) = \frac{g(t) W_m(t)}{W(t)}, \quad m = 1, 2, \dots, n \end{equation*}

where $W_m$ is the determinant of obtained from $W$ by replacing the m-th column by $(0, 0, \dots, 1)^T$. This gives us the particular solution

\begin{equation*} y_p(t) = \sum_{m=1}^{n} y_m(t) \int_{t_0}^t \frac{g(s) W_m(s)}{W(s)} \ ds \end{equation*}

where $t_0$ is arbitrary.

Suppose you have a non-homogenous differential equation of the form

\begin{equation*} y'' + p(t) y' + q(t) y = g(t) \end{equation*}

and we want to find the general solution, i.e. a lin. comb. of the solutions to the corresponding homogenous diff. eqn. and a particular solution. Suppose that we find the solution of the homogenous dif. eqn. to be

\begin{equation*} c_1 y_1(t) + c_2 y_2(t) \end{equation*}

The idea in the method of variation of parameters is that we replace the constants $c_1$ and $c_2$ in the homogenous solution with functions $u_1(t)$ and $u_2(t)$ which we want to produce solutions to the non-homogenous diff. eqn. that are independent to the solutions obtained for the homogenous diff. eqn.

Substituting $u_1(t) y_1(t) + u_2(t) y_2(t)$ into the non-homogenous diff. eqn. we eventually get

\begin{equation*} u_1'(t) y_1(t) + u_2'(t) y_2(t) = g(t) \end{equation*}

which we can solve to obtain our general solution for the non-homogenous diff. eqn.

If the functions $p, q$ and $g$ are continuous on an open interval $I$, and if the functions $y_1$ and $y_2$ are a fundamental set of solutions of the homogenous differential equation corresponding to the non-homogenous differential equation of the form

\begin{equation*} y'' + p(t) y' + q(t) y = g(t) \end{equation*}

then a particular solution is

\begin{equation*} y_p(t) = - y_1(t) \int_{t_0}^{t} \frac{y_2(s) g(s)}{W(y_1, y_2)(s)} \ ds + y_2 \int_{t_0}^{t} \frac{y_1(s) g(s)}{W(y_1, y_2)(s)} \ ds \end{equation*}

where $t_0$ is any conventional chosen point in $I$. The general solution is

\begin{equation*} y = c_1 y_1 (t) + c_2 y_2(t) + y_p(t) \end{equation*}

Parseval's Theorem

The square norm $\langle f, f \rangle$ of a periodic function with convergent Fourier series

\begin{equation*} f(x) = \sum_{n=-\infty}^{\infty} c_n e^{in \pi x / L} \end{equation*}

satisfies

\begin{equation*} \begin{split} \langle f, f \rangle &= \int_{-L}^{L} |f(x)|^2 \ dx = 2L \sum_{n=-\infty}^{\infty} |c_n|^2 \\ &= L \Bigg[ \frac{|a_0|^2}{2} + \sum_{n=1}^{\infty} \Big( |a_n|^2 + |b_n|^2 \Big) \Bigg] \end{split} \end{equation*}

By definition and linearity,

\begin{equation*} \begin{split} \langle f, f \rangle &= \sum_{n, m = - \infty}^{\infty} \int_{-L}^{L} c_n c_m^* e^{i (n - m) \pi x / L} \ dx \\ &= \sum_{n, m = -\infty}^{\infty} c_n c_m^* 2 L \delta_{mn} \qquad \textcolor{red}{\text{orthogonality}} \\ &= 2 L \sum_{n=-\infty}^{\infty} |c_n|^2 \end{split} \end{equation*}

For the last equality, we just need to remember that

\begin{equation*} \begin{split} c_n = \frac{a_n - ib_n}{2}, &\quad c_{-n} = \frac{a_n + ib_n}{2} \\ c_0 &= \frac{a_0}{2} \end{split} \end{equation*}

Indeed,

\begin{equation*} \begin{split} 2 L \sum_{n = -\infty}^{\infty} |c_n|^2 &= 2 L \Bigg[ |c_0|^2 + \sum_{n = 1}^{\infty} \Big( |c_n|^2 + |c_{-n}|^2 \Big) \Bigg] \\ &= 2 L \Bigg[ \frac{|a_0|^2}{4} + \sum_{n=1}^{\infty} \Bigg( \frac{|a_n|^2 + |b_n|^2}{4} + \frac{|a_n|^2 + |b_n|^2}{4} \Bigg) \Bigg] \\ &= L \Bigg[ \frac{|a_0|^2}{2} + \sum_{n=1}^{\infty} \Big( |a_n|^2 + |b_n|^2 \Big) \Bigg] \end{split} \end{equation*}

We also have a Parseval's Identity for Sturm-Liouville problems:

\begin{equation*} \int_{0}^{1} r(x) |f(x)|^2 \ dx = \sum_{n} |c_n|^2 \end{equation*}

where the set $\{ c_n \}$ is determined as

\begin{equation*} c_n = \int_{0}^{1} r(x) f(x) \phi_n(x) \ dx \end{equation*}

and $\phi_n$ are the corresponding eigenfunctions of the SL-problem.

The proof is a simple use of the orthogonality of the eigenfunctions.

Binomial Theorem

Let $\alpha$ be a real number and $k$ a postive integer. Further, define

\begin{equation*} {\alpha \choose k} = \frac{\alpha (\alpha - 1) \dots (\alpha - k + 1)}{k!} \end{equation*}

Then, if $\alpha \in \mathbb{Q}$,

\begin{equation*} (1 + x)^{\alpha} = \sum_{n=0}^{\infty} {\alpha \choose k} x^{k} \end{equation*}

which converges for $|x| < 1$.

This is due to the Mclaurin expansion (Taylor expansion about $x = 0$).

Definitions

Words

bifurication
the appearance of a new solution at a certain parameter value

Wronskian

For a set of solutions $\{y_1, y_2, \dots, y_n\}$, we have

\begin{equation*} W[y_1, \dots, y_n] := \begin{vmatrix} y_1 & y_2 & \dots & y_n \\ y_1' & y_2' & \dots & y_n' \\ \vdots & \vdots & \vdots & \vdots \\ y_1^{(n-1)} & y_2^{(n-1)} & \dots & y_n^{(n-1)} \end{vmatrix} \end{equation*}

i.e. the Wronskian is just the determinant of the solutions to the ODE, which we can then use to tell whether or not the solutions are linearly independent, i.e. if $W[y_1, y_2, \dots, y_n] \ne 0$ we have lin. indep. solutions and thus a unique solution for all initial conditions.

Why?

If you look at the Wronskian again, it's the determinant of the matrix representing the system of linear equations used to solve for a specific vector of initial conditions (if you set the matrix we're taking the determinant of above equal to some $\mathbf{y}_0$ which is the initial conditions).

The determinant of this system of linear equations then tells if it's possible to assign coefficients to these different solutions $y_i$ s.t. we can satisfy any initial conditions, or more specific, there exists a unique solution for each initial condition!

  • if $W[y_1, \dots, y_n] \ne 0$ then the system of linear equations is an invertible matrix, and thus we have a unique solution for each $\mathbf{y}_0$
  • if $W[y_1, \dots, y_n] = 0$ we do NOT have a unique solution for each initial condition $\mathbf{y}_0$

Thus we're providing an answer to the question: do the linear combination of $y_1, \dots, y_n$ include all possible equations?

Properties
  1. If $W[y_1, \dots, y_n] \ne 0$ then $W[y_1, \dots, y_n](x) \ne 0$ for all $x \in [\alpha, \beta]$
  2. Any solution $y(x)$ can be written as a lin. comb. of any fundamental set of solutions $\{y_i(x)\}$
  3. The solutions $\{y_i(x)\}$ form a fundamental set iff they are linearly independent
Proof of property 1

If $W(x_0) \ne 0$ somewhere, $W(x) \ne 0$ everywhere for $x \in [\alpha, \beta]$

Assume $W(x_*) = 0$ at $x=x_*$

Consider

\begin{equation*} \begin{cases} c_1 y_1(x_*) + \dots + c_n y_n(x_*) = 0 \\ c_1 y_1'(x_*) + \dots + c_n y_n(x_*) = 0 \\ \dots \\ c_1 y_1^{(n-1)}(x_*) + \dots + c_n y_n^{(n-1)}(x_*) = 0 \end{cases} \end{equation*}

which can be written

\begin{equation*} A \mathbf{c} = 0 \end{equation*}

with $\det A = W(x_*) = 0$

Hence, $\exists(c_1, \dots, c_n) \neq (0, \dots, 0)$ such that (*) holds.

Thus, we can construct $y(x) = c_1 y_1(x) + \dots + c_n y_n(x)$ which satisfies the ODE at $x = x_*$

Proof of property 2

We want to show that $c_1 y_1 (x) + \dots + c_n y_n (x)$ can satisfy any

\begin{equation*} A \mathbf{c} = \mathbf{y}_0 \end{equation*}

Linearly independent → $\det A \ne 0$ and since $\det A = W(x_0)$, by property 1 we can solve it.

Homogenenous n-th order linear ODEs

\begin{equation*} L[y] = \frac{d^n y}{dx^n} + p_1(x) \frac{d^{n - 1} y}{dx^{n-1}} + \dots \ p_{n-1}(x) \frac{dy}{dx} + p_n(x) y = 0 \end{equation*}

Solutions $y_j$ to homogeneous ODEs forms a vector space

Non-homogeneous n-th order linear ODEs

\begin{equation*} L[y] = \frac{d^n y}{dx^n} + p_1(x) \frac{d^{n - 1} y}{dx^{n-1}} + \dots \ p_{n-1}(x) \frac{dy}{dx} + p_n(x) y = g(x) \end{equation*}
Solution
  1. Solve the corresponding homogeneous linear ODE
  2. Find special case solution for the non-homogeneous
  3. General solution is then the linear combination of these
  • Simple case

    In the simple case of one variable:

    \begin{equation*} y = \phi(t) = c_1 y_1 (t) + c_2 y_2(t) + Y(t) \end{equation*}

    where $y_1$ and $y_2$ are a fundamental set of solutions of the corresponding homogenous equation, and $Y$ is some specific solution to the non-homogenous equation.

Power series

\begin{equation*} y(x) = \sum_{n=0}^\infty a_n (x - x_0)^n \end{equation*}

Laplace transform

An integral transform is a relation of the form

\begin{equation*} F(s) = \int_\alpha^\beta K(s, t) f(t) \ dt \end{equation*}

where $K(s, t)$ is a given function, called the kernel of the transformation, and the limits of integration $\alpha$ and $\beta$ are also given.

Suppose that

  1. $f$ is piecewise continuous on the interval $0 \le t \le A$ for any positive $A$.
  2. $|f(t)| \le K e^{at}$ when $t \ge M$. In this inequality, $K$, $a$, and $M$ are real constants, $K$ and $M$ necessarily positive.

Then the Laplace transform of $f$, denoted $\mathcal{L}\{f(t)\}$ or by $F(s)$, is defined

\begin{equation*} \mathcal{L}\{f(t)\} = F(s) = \int_0^\infty e^{-st} f(t) \ dt \end{equation*}

and exists for $s \ge a$.

Under these restrictions a function $f(t)$ which increases faster than $Ke^{at}$ is does not converge and thus the Laplace transform is not defined for this $f(t)$.

Properties
  • Identities

    Let $\mathcal{L}\{f(x)\}(s) = F(s)$, for $f \in E$

    • S-shift
      \begin{equation*} \mathcal{L}\{e^{-cx} f(x)\}(s) = F(s + c) \end{equation*}
    • X-shift

      If $c \ge 0$ and $f(x) = 0$ for $x < 0$:

      \begin{equation*} \mathcal{L}\{f(x - c)\}(s) = e^{-sc}F(s) \end{equation*}
    • S-derivative
      \begin{equation*} \mathcal{L}\{xf(x)\}(s) = - F'(s) \end{equation*}

      or more generally,

      \begin{equation*} \mathcal{L}\{x^n f(x)\} = - \frac{d^n \mathcal{L}\{f(x)\}}{ds^n} \end{equation*}
    • Scaling

      If $c > 0$:

      \begin{equation*} \mathcal{L}\{f(cx)\}(s) = \frac{1}{c} F(s / c) \end{equation*}
      \begin{equation*} F(sc) = \frac{1}{c} \mathcal{L}\{f(x / c)\} \end{equation*}
  • Linear operator

    The Laplace transform is a linear operator:

    \begin{equation*} \mathcal{L}{f_1(t) + f_2(t)} = \mathcal{L}{f_1(t)} + \mathcal{L}{f_2(t)} \end{equation*}
  • Uniqueness of transform

    We can use the Laplace transform to solve a differential equation, and by

  • Inverse is linear operator

    Frequently, a Laplace transform $F(s)$ is expressible as a sum of serveral terms

    \begin{equation*} F(s) = F_1(s) + F_2(s) + \dots + F_n(s) \end{equation*}

    Suppose that $f_1(t) = \mathcal{L}^{-1}\{F_1(s)\}, \dots, f_n(t) = \mathcal{L}^{-1}\{F_n(s)\}$. Then the function

    \begin{equation*} f(t) = f_1(t) + \dots + f_n(t) \end{equation*}

    has the Laplace transform $F(s)$. By the uniqueness property stated previously, no other continuous function $f$ has the same transform. Thus

    \begin{equation*} \mathcal{L}^{-1}\{F(s)\} = \mathcal{L}^{-1}\{F_1(s)\} + \dots + \mathcal{L}^{-1}\{F_n(s)\} \end{equation*}

    that is, the inverse Laplace transform is also a linear operator.

Solution to IVP

Suppose that functions $f, f', \dots, f^{(n-1)}$ are continuous and that $f^{(n)}$ is piecewise continuous on any interval $0 \le t \le A$. Suppose further that

\begin{equation*} \exists K, a, M \quad : \quad |f(t)| \le Ke^{at}, |f'(t)| \le Ke^{at}, \dots, |f^{(n-1)}| \le Ke^{at} \quad t \ge M \end{equation*}

Then $\mathcal{L}\{f(t)\}$ exists for $s > a$ and is given by

\begin{equation*} \mathcal{L}\{f^{(n)}(t)\} = s^n \mathcal{L}\{f(t)\} - s^{n-1} f(0) - \dots - s f^{(n-2)}(0) - f^{(n-1)}(0) \end{equation*}

We only prove it for the first derivative case, since this can then be expanded for the nth order derivative.

Consider the integral

\begin{equation*} \int_0^A e^{-st} f'(t) \ dt \end{equation*}

whose limit as $A \to \infty$, if it exists, is the Laplace transform of $f'$.

Suppose $f'$ is piecewise continuous, we can partition the interval and write the integral as follows

\begin{equation*} \int_0^A e^{-st} f'(t) \ dt = \int_0^{t_1} e^{-st} f'(t) \ dt + \int_{t_1}^{t_2} e^{-st} f'(t) \ dt + \dots + \int_{t_{k}}^{A} e^{-st} f'(t) \ dt \end{equation*}

Integrating each term on the RHS by parts yields

\begin{equation*} \begin{split} \int_0^A e^{-st} f'(t) \ dt =& e^{-st} f(t) \Big|_0^{t_1} + e^{-st} f(t) \Big|_{t_1}^{t_2} + \dots + e^{-st} f(t) \Big|_{k}^{A} \\ & + \Bigg[ \int_0^{t_1} e^{-st} f(t) \ dt + \int_{t_1}^{t_2} e^{-st} f(t) \ dt + \dots + \int_{t_k}^{A} e^{-st} f(t) \ dt \Bigg] \end{split} \end{equation*}

since $f$ is continuous, the contributions of the integrated terms at $t_1, t_2, \dots, t_k$ cancel, and we can combine the integrals into a single integral, again due to continuity:

\begin{equation*} \int_0^A e^{-st} f'(t) \ dt = e^{-sA} f(A) - f(0) + s \int_0^A e^{-st}f(t) \ dt \end{equation*}

Now finally letting $A \to \infty$ (since that's what we do in the Laplace tranform ) we note that

\begin{equation*} \underset{A \to \infty} s \int_0^A e^{-st} f(t) \ dt = \mathcal{L}{f(t)} \end{equation*}

And since $A \ge M$, we have $|f(A) \le K e^{at}$ ; consequently

\begin{equation*} |e^{-sA} f(A)| \ge Ke^{-(s -a ) A} \implies \underset{A \to \infty}{\lim} e^{-sA}f(A) \to 0, \quad \text{when } s > a \end{equation*}

Finally giving us

\begin{equation*} \mathcal{L}{f'(t)} = s \mathcal{L}{f(t)} - f(0) \end{equation*}
Typical ones
Examples:

Fourier Series

Given a periodic function $f(x)$ with period $2L$, it can be expressed as a Fourier series

\begin{equation*} f(x) = \frac{a_0}{2} + \sum_{n=1}^{\infty} \Bigg( a_n \cos \frac{n \pi x}{L} + b_n \sin \frac{n \pi x}{L} \Bigg) \end{equation*}

where the coefficients are given by

\begin{equation*} \begin{split} a_n = \frac{1}{L} \int_{-L}^{L} f(x) \cos \frac{\pi n x}{L} \ dx \\ b_n = \frac{1}{L} \int_{-L}^{L} f(x) \sin \frac{\pi n x}{L} \ dx \end{split} \end{equation*}

Suppose $f(x)$ and $f'(x)$ are piecewise continuous for $x \in [-L, L]$.

Suppose $f(x)$ is defined outside the interval so that it is periodic with period $2L$. Then the Fourier series of $f(x)$ converges to $f(x)$ where $f(x)$ is continuous and to $\big( f(x^+) + f(x^-) \big) / 2$ where $f(x)$ is discontinuous.

Heavside function

\begin{equation*} u_c(t) = \begin{cases} 0& \quad t < c \\ 1& \quad t \le c \end{cases} \end{equation*}

Which has a discontinuity at $t=c$.

Convolution integral

If $f(t)$ and $g(t)$ are piecewise continuous functions on $[0, \infty)$ then the convolution integral of $f(t)$ and $g(t)$ is,

\begin{equation*} (f * g) (t) = \int_0^t f(t - \tau)g(t) \ d \tau \end{equation*}
Laplace transform
\begin{equation*} \mathcal{L}\{f * g\} = F(s) G(s) \end{equation*}

Phase plane

A phase plane is a visual display of certain characteristics of certain kinds of differential equations; a coodinate plane with axes being the values of the two state variables, e.g. $(x, y)$.

It's a two-dimensional case of the general n-dimensional phase space .

Trajectory

A trajectory $\boldsymbol{\phi}(t)$ of a system

\begin{equation*} \mathbf{x}'(t) = \mathbf{g}(\mathbf{x}) \end{equation*}

simply refers to a solution for some specific initial conditions $\mathbf{c}$, i.e.

\begin{equation*} \boldsymbol{\phi}(0) = \mathbf{c} \end{equation*}

Critical points

Points corresponding to constant solutions or equilibrium solutions, of the following equation

\begin{equation*} \frac{d \mathbf{x}}{dt} = \mathbf{g}(\mathbf{x}) \end{equation*}

are often called critical points.

That is, points $\mathbf{x}_0$ such that

\begin{equation*} \frac{d \mathbf{x}}{dt} = 0 \quad \iff \quad 0 = \mathbf{g}(\mathbf{x}_0) \end{equation*}

There always exists a coordinate transformation $\mathbf{y} = \mathbf{x} - \mathbf{x}_0$, such that

\begin{equation*} \frac{d \mathbf{y}}{d t} = \frac{d \mathbf{x}}{dt} = \mathbf{g}(\mathbf{y}) = \mathbf{g}(\mathbf{y} + \mathbf{x}_0) = \mathbf{f}(\mathbf{x}) \end{equation*}

such that the new system

\begin{equation*} \frac{d \mathbf{y}}{d t} = \mathbf{f}(\mathbf{x}), \quad \mathbf{f}(\mathbf{0}) = \mathbf{0} \end{equation*}

has an equilibrium solution or critical point at the origin.

Special differential equations / solutions

Legendre equation

The Legendre equation is given below:

\begin{equation*} (1 - x^2) y'' - 2x y' + \ell (\ell + 1) y = 0 \end{equation*}

We only need to consider $\ell > -1$ since if $\ell < -1$ we can reparametrize the equation to be of the form above anyways.

In the case where we assume $\ell \in \mathbb{N}$, we note that for even $\ell$ $y_1$ becomes a terminating series, rather than an infinite series, and if $\ell$ is odd $y_2$ is a terminating series, i.e. in both cases we get a polynomial of order $\ell$ !

These polymomials corresponding to a solution of the Legendre equation for a specific integer $\ell$ we call a Legendre Polynomial, denoted $P_{\ell}(x)$.

\begin{equation*} P_{\ell}(x) = \frac{1}{2^{\ell} \ell!} \frac{d^{\ell}}{dx^{\ell}} \Big[ (x^2 - 1)^{\ell} \Big] \end{equation*}

Or the general Legendre equation :

\begin{equation*} (1 - x^2) y'' - 2x y' + \Bigg[ \ell (\ell + 1) - \frac{m^2}{1 - x^2} \Bigg] y = 0 \end{equation*}

Which gives rise to the polynomials defined

\begin{equation*} P_{\ell}^m(x) = (-1)^m (1 - x^2)^{m / 2} \frac{d^m}{dx^m} \Big( P_{\ell}(x) \Big) \end{equation*}

where $P_{\ell}(x)$ are the corresponding Legendre polynomial.

Moreover, using Rodrigues formula

\begin{equation*} P_{\ell}^m(x) = \frac{(-1)^m}{2^{\ell} \ell !} (1 - x^2)^{m / 2} \frac{d^{\ell + m}}{dx^{\ell + m}} (x^2 - 1)^{\ell} \end{equation*}

If we let $- \ell \le m \le \ell$ we can use the relationship between $P_{\ell}^{\pm m}(x)$

\begin{equation*} \frac{d^{\ell - m}}{dx^{\ell - m}} (x^2 - 1)^{\ell} = c_{\ell m} (1 - x^2)^m \frac{d^{\ell + m}}{dx^{\ell + m}} (x^2 - 1)^{\ell} \end{equation*}

to obtain the coefficient

\begin{equation*} P_{\ell}^{-m}(x) = (-1)^m \frac{(\ell - m)!}{(\ell + m)!} P_{\ell}^{m}(x) \end{equation*}

Series Solutions

The sum of the even terms is given by:

\begin{equation*} y_1(x) = 1 + \sum_{m=1}^{\infty} (-1)^m \frac{(\alpha + 2m - 1) (\alpha + 2m - 3) \cdots (\alpha + 1) \alpha (\alpha - 2) \cdots (\alpha - 2m + 2)}{(2m)!} x^{2m} \end{equation*}

and the sum of the odd terms are given by:

\begin{equation*} y_2(x) = x + \sum_{m=1}^{\infty} (-1)^m \frac{(\alpha + 2m)(\alpha + 2m - 2) \cdots (\alpha + 2) (\alpha - 1)(\alpha - 3) \cdots (\alpha - 2m + 1)}{(2m + 1)!} x^{2m + 1} \end{equation*}

TODO Legendre polynomials and Laplace equation using spherical coordinates

Van der Pol oscillator

\begin{equation*} x'' - \mu (1 - x^2) x' + x = 0 \end{equation*}

where $x$ is the position coordinate, which is a function of time $t$, and $\mu$ is a scalar parameter indicating the nonlinearity and the strength of the damping.

Hermite polynomials

We are talking about the physicsts' Hermite polynomials given by

\begin{equation*} H_n(x) = (-1)^n e^{x^2} \frac{d^n}{dx^n} e^{-x^2} = \Bigg( 2x - \frac{d}{dx} \Bigg)^n \cdot 1 \end{equation*}

These are a orthonormal polynomial sequence, and they arise from the differential equation

\begin{equation*} y'' - 2x y' = - 2 \lambda y \end{equation*}

These polynomials are orthogonal wrt. the weight function $w(x) = e^{x^2}$, i.e. we have

\begin{equation*} \int_{-\infty}^\infty H_m(x) H_n(x) w(x) dx = 2^n \sqrt{\pi} \ n! \ \delta_{mn}, \quad \forall m \ne n \end{equation*}

Furthermore, the Hermite polynomials form an orthogonal basis of a the Hilbert space of functions satisfying

\begin{equation*} \int_{-\infty}^\infty |f(x)|^2 w(x) < \infty \end{equation*}

in which the inner product is given by the integral including the Gaussian inner product defined previously:

\begin{equation*} \langle f, g \rangle = \int_{-\infty}^\infty f(x) \overline{g(x)} w(x) dx \end{equation*}

Spherical harmonics

In this section we're looking to tackle the spherical harmonics once and for all.

If we have a look at the Laplace equation in spherical coordinates, we have

\begin{equation*} \nabla^2 f = \frac{1}{r^2} \pdv{r} \Bigg( r^2 \pdv{f}{r} \Bigg) + \frac{1}{r^2 \sin \theta} \pdv{\theta} \Bigg( \sin \theta \pdv{f}{\theta} \Bigg) + \frac{1}{r^2 \sin^2 \theta} \frac{\partial^2 f}{\partial \theta^2} = 0 \end{equation*}

If we then use separation of variables, and consider solutions of the form:

\begin{equation*} f(r, \theta, \phi) = R(r) Y(\theta, \phi) \end{equation*}

We get the following differential equations:

\begin{equation*} \begin{split} \frac{1}{R} \frac{\dd}{\dd{r}} \Bigg( r^2 \frac{\dd{R}}{\dd{r}} \Bigg) &= \lambda \\ \frac{1}{Y} \frac{1}{\sin \theta} \pdv{\theta} \Big( \sin \theta \pdv{Y}{\theta} \Big) + \frac{1}{Y} \frac{1}{\sin^2 \theta} \frac{\partial^2 Y}{\partial \phi^2} &= - \lambda \end{split} \end{equation*}

Further, assuming $Y(\theta, \phi) = \Theta(\theta) \Phi(\phi)$, we can rewrite the second differential equation as

\begin{equation*} \begin{split} \frac{1}{\Phi} \frac{\dd^2 \Phi}{\dd \phi^2} &= -m^2 \\ \lambda \sin^2 \theta + \frac{\sin \theta}{\Theta} \frac{\dd}{\dd \theta} \Bigg( \sin \theta \frac{\dd \Theta}{\dd \theta} \Bigg) &= m^2 \end{split} \end{equation*}

for some number $m$.

Solving for $R$

First we take a look at the differential equation involving $R$,

\begin{equation*} \frac{1}{R} \frac{\dd}{\dd{r}} \Bigg( r^2 \frac{\dd{R}}{\dd{r}} \Bigg) = \lambda \end{equation*}

Which we can rewrite as

\begin{equation*} r^2 R'' + 2 r R' - \lambda R = 0 \end{equation*}

making the substitution

\begin{equation*} x = \ln r \end{equation*}

This is fine, since in spherical coordinates we have $0 < r < \infty$, i.e. $\ln r$ is always defined.

Thus,

\begin{equation*} \begin{split} R' &= \frac{d R}{d x} \frac{d x}{d r} = \frac{1}{r} \frac{d R}{d x} \\ R'' &= \frac{d}{dr} \Bigg( \frac{1}{r} \frac{d R}{d x} \Bigg) = - \frac{1}{r^2} \frac{d R}{d x} + \frac{1}{r} \Bigg( \frac{d x}{d r} \frac{d }{d x} \Big( \frac{d R}{d x} \Big) \Bigg) \\ &= - \frac{1}{r^2} \frac{d R}{d x} + \frac{1}{r^2} \frac{d^2 R}{d x^2} \end{split} \end{equation*}

Substituting back into the differential equation, we get

\begin{equation*} \frac{d^2 R}{d x^2} + \frac{d R}{d x} - \lambda R = 0 \end{equation*}

which has the general solution

\begin{equation*} R(r) = A r^\ell + B r^{- (\ell + 1)} \end{equation*}

where

\begin{equation*} \ell = \frac{-1 + \sqrt{1 + 4 \lambda}}{2} \end{equation*}

solves

\begin{equation*} \ell^2 + \ell - \lambda = 0 \end{equation*}

or rather,

\begin{equation*} \lambda = \ell (\ell + 1) \end{equation*}

RECOGNIZE THIS YO?! How about trying to substitute this into the differential equation involving $\Theta$?

Solving for $\Phi$

The differential equation with $\Phi$ can be written

\begin{equation*} \Phi'' + m^2 \Phi = 0 \end{equation*}

which has the solution

\begin{equation*} \Phi(\phi) = A \cos m \phi + B \sin m \phi = C e^{im \theta} + D e^{- im \theta} \end{equation*}

Further, we have the boundary condition $\Phi(\phi) = \Phi(\phi + 2 \pi)$, which implies $m \in \mathbb{N}$.

Solving for $\Theta$

We have the the ODE

\begin{equation*} \lambda \sin^2 \theta + \frac{\sin \theta}{\Theta} \frac{\dd}{\dd \theta} \Bigg( \sin \theta \frac{\dd \Theta}{\dd \theta} \Bigg) = m^2 \end{equation*}

which we can write out to get

\begin{equation*} \textcolor{blue}{\Theta \lambda \sin^2 \theta} + \sin \theta \Big( \textcolor{green}{\Theta' \cos \theta} + \textcolor{red}{\Theta'' \sin \theta} \Big) = m^2 \Theta \end{equation*}

Making the substitution $x = \cos \theta$ we have

\begin{equation*} \textcolor{green}{\frac{d \Theta}{d \theta}} = \frac{d \Theta}{d x} \frac{d x}{d \theta} = \big( - \sin \theta \big) \frac{d \Theta}{d x} \end{equation*}

And,

\begin{equation*} \begin{split} \textcolor{red}{\frac{d^2 \Theta}{d \theta^2}} &= \frac{d }{d \theta} \Big( \big( - \sin \theta \big) \frac{d \Theta}{d x} \Big) \\ &= \big( - \cos \theta \big) \frac{d \Theta}{d x} + \big( - \sin \theta \big) \frac{d^2 \Theta}{d x^2} \frac{d x}{d \theta} \\ &= \big( - \cos \theta \big) \frac{d \Theta}{d x} + \sin^2 \theta \frac{d^2 \Theta}{d x^2} \\ &= - x \frac{d \Theta}{d x} + (1 - \cos^2 \theta) \frac{d^2 \Theta}{d x^2} \\ &= - x \frac{d \Theta}{d x} + (1 - x^2) \frac{d^2 \Theta}{d x^2} \end{split} \end{equation*}

Substituting back into the ODE from above:

\begin{equation*} \begin{split} \textcolor{blue}{\Theta \lambda \sin^2 \theta} \textcolor{green}{- \sin^2 \theta \cos \theta \frac{d \Theta}{d x}} \textcolor{red}{- \sin^2 \theta \cos \theta \frac{d \Theta}{d x} + \big( \sin^2 \theta \big)^2 \frac{d^2 \Theta}{d x^2}} &= m^2 \Theta \\ \textcolor{blue}{\Theta \lambda} \textcolor{green}{- 2 \cos \theta \frac{d \Theta}{d x}} \textcolor{red}{+ \sin^2 \theta \frac{d^2 \Theta}{d x^2}} &= \frac{m^2}{\sin^2 \theta} \Theta \end{split} \end{equation*}

Observing that

\begin{equation*} \sin^2 \theta = 1 - \cos^2 \theta = 1 - x^2 \end{equation*}

We can write the above equation as

\begin{equation*} \textcolor{blue}{\lambda \Theta} - \textcolor{green}{2 x \frac{d \Theta}{d x}} + \textcolor{red}{(1 - x^2) \frac{d^2 \Theta}{d x^2}} = \frac{m^2}{1 - x^2} \Theta \end{equation*}

Whiiiich, we recognize as the general Legendre differential equation!

\begin{equation*} (1 - x^2) \frac{d^2 \Theta}{dx^2} - 2x \frac{d \Theta}{dx} + \Big( \lambda - \frac{m^2}{1 - x^2} \Big) \Theta = 0 \end{equation*}

where we're only lacking the $\lambda = \ell (\ell + 1)$, for which we have to turn to the differential equation involving $R(r)$.

With $\lambda = \ell (\ell + 1)$ obtained from Solving for $R$, we can rewrite the differential equation involving $\Theta$ as

\begin{equation*} (1 - x^2) \frac{d^2 \Theta}{dx^2} - 2x \frac{d \Theta}{d x} + \Big( \ell (\ell + 1) - \frac{m^2}{1 - x^2} \Big) \Theta = 0, \qquad -1 < x < 1 \end{equation*}

For which we know that the solutions are the corresponding associated Legendré polynomials

\begin{equation*} \Theta(\theta) = P_\ell^m(x) = P_\ell^m(\cos \theta) \end{equation*}

which are obtained by considering the series solution of the equation above, i.e. assuming:

\begin{equation*} y(x) = \sum_{n=1}^{\infty} a_n x^n \end{equation*}

where $x$ is as above. Substituting into the differential equation above, and finding the recurrence-relation for $a_n$ we recover the Legendre polynomials mentioned above.

Bringing $\Phi$ and $\Theta$ together

Now, finally bringing this together with the solution obtained for $\Phi$, we have the spherical harmonics

\begin{equation*} Y_\ell^m( \theta, \phi) = c_\ell^m P_\ell^m (\cos \theta) e^{im \phi} \end{equation*}

where $c_\ell^m$ is simply the normalization constant to such that the eigenfunctions form a basis, which turns out to be

\begin{equation*} c_\ell^m = \sqrt{\frac{2 \ell + 1}{4 \pi} \frac{(\ell - m)!}{(\ell + m)!}} \end{equation*}

Thus, the final expression for the spherical harmonics is

\begin{equation*} Y_\ell^m(\theta, \phi) = \sqrt{\frac{2 \ell + 1}{4 \pi} \frac{(\ell - m)!}{(\ell + m)!}} P_\ell^m(\cos \theta) e^{im \phi} \end{equation*}

Combining everything

Finally, combining the radial solution and the spherical harmonics into the final expression for our solutions:

\begin{equation*} f_\ell^m(r, \theta, \phi) = R(r) Y_\ell^m(\theta, \phi) = r^\ell Y_\ell^m(\theta, \phi) \end{equation*}

where we have set $B = 0$ to ensure regularity at $r = 0$, and not have the following occur:

\begin{equation*} \lim_{r \to 0} R(r) = \lim_{r \to 0} \Big( A r^\ell + B r^{- (\ell + 1)} \Big) = A \lim_{r \to 0} r^\ell + B \lim_{r \to 0} r^{- (\ell + 1)} = B \lim_{r \to 0} r^{- (\ell + 1)} = \infty \end{equation*}

Boundary conditions

  1. Establish that $\Phi$ must be periodic (since we're working in spherical coordinates) whose period evenly divides $2 \pi$, which implies $m \in \mathbb{N}$ and $\Phi$ is a linear combination of $e^{\pm im \phi}$
  2. Using what we observed in 1. and noting that $Y(\theta, \phi)$ is "regular" at the poles of the sphere, where $\theta = 0, \pi$, we have a boundary condition for $\Theta$ (which is a Sturm-Liouville problem) forcing the parameter $\lambda$ to be of the form $\lambda = \ell ( \ell + 1)$
  3. Making the change of variables $t = \cos \theta$ trnasforms this equation into the general Legendre equation, whose solution is a multiple of the associated Legendre Polynomial.

  4. Finally, the equation for $R$ has solutions of the form

    \begin{equation*} R = A r^{\ell} + B r^{- \ell - 1} \end{equation*}
  5. If we want the solution to be "regular" throughout $\mathbb{R}^3$, we have $B = 0$.

When we say regular, we mean that the solution $f(r, \theta, \phi)$ has the property

\begin{equation*} |f(r, \theta, \phi)| < \infty \end{equation*}
Proper description

A priori $m$ is a complex number, BUT because $\Phi$ must be a periodic function whose period evenly divides $2 \pi$, $m$ is necessarily an integer and $\Phi$ is a linear combination of the complex exponentials $e^{\pm im \phi}$.

Further, the solution function $Y(\theta, \phi)$ is regular at the poles of the sphere, where $\theta = 0, \pi$. Imposing this regularity in the solution $\Theta$ of the second equation at the boundary of the domain is a Sturm-Liouville problem that forces the parameter $\lambda$ to be of the form

\begin{equation*} \lambda = \ell (\ell + 1), \quad \ell \ge |m|, \quad \ell \in \mathbb{N} \end{equation*}

Furthermore, a change of variables $t = \cos \theta$ transforms this equation into the (general) Legendre equation, whose solution is a multiple of the associated Legendre polynomial $P_{\ell}^m(\cos \theta)$.

Finally, the equation for $R$ has solutions of the form

\begin{equation*} R(r) = A r^{\ell} + B r^{- \ell - 1} \end{equation*}

And if we require $R(r)$ solution to be regular throughout $\mathbb{R}^3$ forces $B = 0$.

Solutions

Here, the solution assumed to have the special form $Y(\theta, \phi) = \Theta(\theta) \Phi(\phi)$. For a given value of $\ell$, there are $2 \ell + 1$ independent solutions of this form, one for each integer $-\ell \le m \le \ell$. These angular solutions are a product of trigonometric functions, here represented as a complex exponential, and associated Legendre polynomials:

\begin{equation*} Y_{\ell}^m (\theta, \phi) = N e^{im \phi} P_{\ell}^m(\cos \theta) \end{equation*}

which fulfill

\begin{equation*} r^2 \nabla^2 Y_{\ell}^m (\theta, \phi) = - \ell (\ell + 1) Y_{\ell}^m (\theta, \phi) \end{equation*}

The general solution to the Laplace's equation in a ball centered at the origin is a linear combination of the spherical harmonic functions multiplied by the appropriate scale factor $r^{\ell}$,

\begin{equation*} f(r, \theta, \phi) = \sum_{\ell = 0}^{\infty} \sum_{m = - \ell}^{\ell} f_{\ell}^m r^{\ell} Y_{\ell}^m(\theta, \phi) \end{equation*}

where the $f_{\ell}^m$ are constants the factors $r^{\ell} Y_{\ell}^m$ are known as solid harmonics.

Q & A

DONE Why do we actually require the $\ell$ to be an integer?

In solving for $\Phi$ we observe that

\begin{equation*} \Phi(\phi) = A \cos m \phi + B \sin m \phi = C e^{im \theta} + D e^{- im \theta} \end{equation*}

Thus, if we require $\Phi(\phi) = \Phi(\phi + 2 \pi)$ to be true, then we need $\Phi$ to "go full circle" every $\pi$, hence $m \in \mathbb{N}$.

If it does NOT go full circle, then it would be discontinuous.

DONE We have TWO explanations for why we need $\lambda = \ell ( \ell + 1)$, which one is true?
  • Question

    Here we state that $\lambda = \ell (\ell + 1)$ has to be "because it's a Sturm-Liouville problem". I don't understand why it being a Sturm-Liouville problem necessarily imposes this restriction.

    Ah! Maybe it's because Sturm-Liouville problems require the limiting behavior of the boundary conditions to satisfy Lagrange's identity being zero!

    While here, we simply solve the differential equation involving $R(r)$, and $\lambda = \ell (\ell + 1)$ just falls out from this solution, and as far as I can tell, we're not actually saying anything about the boundary conditions in this case.

  • Answer

    From what I can understand, the eigenvalue $\lambda = \ell (\ell + 1)$ simply falls out from $R(r)$ as we found, and $\lambda$ being of this form does not seem to be related in any way to boundary conditions.

    What is related to the boundary conditions, the fact that $\ell$ is an integer.

    What is related to the b

Bessel equation

\begin{equation*} y'' + \frac{1}{x} y' + \bigg( 1 - \frac{v^2}{x^2} \bigg) y = 0 \end{equation*}

This can be solved using Frobenius method.

In the case where $v = m \in \mathbb{Z}$, we end up with the Bessel function of the 1st kind :

\begin{equation*} J_m(x) = \bigg( \frac{x}{2} \bigg)^m \sum_{k=1}^{\infty} (-1)^k \frac{x^{2k}}{k! \ (m + k)!} \end{equation*}

And the Bessel function of the 2nd kind :

\begin{equation*} Y_m(x) = \frac{2}{\pi} \log \bigg( \frac{x}{2} \bigg) J_m(x) + \sum_{k=0}^{\infty} \dots x^{2k} \end{equation*}

Thus, the general solution will be the linear combination:

\begin{equation*} R_m(x) = c_1 J_m(x) + c_2 Y_m(x) \end{equation*}

Where we have the following limiting behavior:

\begin{align*} J_0(0) = 1, & \qquad J_m(0) = 0 \quad \text{for} \quad m \ge 1 \\ Y_m(x) \to & - \infty \quad \text{as} \quad x \to 0 \end{align*}

Note: Quite often we want the solution to be "regular" / nicely behaved as $x \to 0$, thus we often end up setting $c_2 = 0$ in the expression for $R_m$.

Problems

10.2 Fourier Series

Ex. 10.2.1

Assume that there is a Fourier series converging to the function $f$ defined by

\begin{equation*} f(x) = \begin{cases} - x,& \quad -2 \le x < 0 \\ x,& \quad 0 \le x < 2 \end{cases} \end{equation*}

with the property that

\begin{equation*} f(x + 4) = f(x) \end{equation*}

i.e. it's periodic with a period of 4.

Find the components of the Fourier series.

Solution
\begin{equation*} \begin{split} f(x) &= 1 - \frac{8}{\pi^2} \sum_{m=1, 3, 5, \dots}^{\infty} \frac{1}{m^2} \cos \Big( \frac{m \pi}{2} x \Big) \\ &= 1 - \sum_{n=1}^{\infty} \frac{\cos (2n - 1) \pi x / 2}{(2n - 1)^2} \end{split} \end{equation*}

See p. 601 in (Boyce, 2013) for the full solution.

10.5 Separation of variables; Heat conduction in a Rod

Find the solution of the heat conduction problem

\begin{equation*} \begin{split} \text{Eqn: } & 100 u_{xx} = u_t, \quad \qquad \qquad \qquad 0 < x < 1, \quad t > 0 \\ \text{BC: } & u(0, t) = 0, \qquad \qquad \qquad \qquad u(1, t) = 0, \quad t > 0 \\ \text{IV: } & u(x, 0) = \sin 2 \pi x - \sin 3 \pi x, \quad 0 \le x \le 1 \end{split} \end{equation*} 1

Solution

\begin{equation*} u(x, t) = e^{400 \pi^2 t} \sin (2n \pi x) - e^{900 \pi^2 t} \sin (3n \pi x) \end{equation*}

We suppose

\begin{equation*} u(x, t) = X(x) T(t) \end{equation*}

And the boundary conditions are satisfied by

\begin{equation*} X(0) = X(1) = 0 \end{equation*}

First we note that with $u(x, t)$ above we get the following

\begin{equation*} 100 X'' T = X T' \end{equation*}

which gives

\begin{equation*} \frac{X''}{X} = \frac{1}{100} \frac{T'}{T} = - \lambda \end{equation*}

for some constant $\lambda$, which gives us the system

\begin{equation*} \begin{cases} X'' + \lambda X &= 0 \\ T' + 100 \lambda T &= 0 \end{cases} \end{equation*}

The solution to the first equation simply gives us

\begin{equation*} X(x) = c_1 \cos \mu x + c_2 \sin \mu x, \quad \lambda = \mu^2 \end{equation*}

Considering the boundary conditions, we get

\begin{equation*} \begin{split} X(0) &= 0 \implies c_1 = 0 \\ X(1) &= 0 \implies \sin \mu = 0 \implies \mu = \pi n \end{split} \end{equation*}

thus we get the eigenfunctions and eigenvalues for $X(x)$:

\begin{equation*} X_n(x) = \sin n \pi x, \quad \lambda_n = \mu_n^2 = n^2 \pi^2 \end{equation*}

Substituting these eigenvalues into the differential equation with $T$:

\begin{equation*} T' + 100 n^2 \pi^2 T = 0 \end{equation*}

which can be solved by use of integrating factors, thus

\begin{equation*} T_n(t) = e^{100 n^2 \pi^2 t} \end{equation*}

Finally, combining both into the eigenfunctions for the entire solution $u_n(x, t)$

\begin{equation*} u_n(x, t) = T_n(t) X_n(x) = e^{100 n^2 \pi^2 t} \sin n \pi x \end{equation*}

Which gives us the general solution:

\begin{equation*} u(x, t) = \sum_{n=1}^{\infty} e^{100n^2\pi^2 t} \sin n \pi x \end{equation*}

and solving for the coefficients using the initial conditions, i.e. when $t = 0$

\begin{equation*} u(x, 0) = \sin 2 \pi x - \sin 3 \pi x \implies c_2 = 1, \quad c_3 = 0, \quad c_i = 0 \text{ if } i \ne 2, 3$ \end{equation*}

Hence the final solution is

\begin{equation*} u(x, t) = e^{400 \pi^2 t} \sin 2 \pi x - e^{900 \pi^2 t} \sin 3 \pi x \end{equation*}