Functional Analysis

Table of Contents

Notation

Definitions

Bounded operator

We say a linear operator $A: \mathbf{H} \to \mathbf{H}$ is bounded if

\begin{equation*} \exists C \in \mathbb{C} : \norm{A \psi} \le C \norm{\psi}, \quad \forall \psi \in \mathbf{H} \end{equation*}

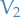If $V_1$ and $V_2$ are normed spaces, a linear map 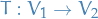$T: V_1 \to V_2$ is bounded if

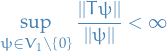
\begin{equation*} \sup_{\psi \in V_1 \setminus \left\{ 0 \right\}} \frac{|| T \psi ||}{||\psi||} < \infty \end{equation*}

If $T$ is bounded, then the supremum above is called the operator norm of $T$, denoted $||T||$.

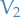Let $V_1$ be a normed space and $V_2$ be a Banach space.

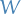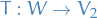Suppose $W$ is a dense subspace of $V_1$ and $T: W \to V_2$ is a bounded linear operator.

Then there exists a unique bounded linear map $\tilde{T} : V_1 \to V_2$ such that

\begin{equation*} \tilde{T} \big|_{W} = T \end{equation*}

Furthermore,

\begin{equation*} ||\tilde{T}|| = ||T|| \end{equation*}

Theorems

Riesz representation theorem

Notation

  • $H$ denotes a Hilbert space

Theorem

This theorem establishes an important connection between a Hilbert space and its continuous dual space.

If the underlying field is $\mathbb{R}$, then the Hilbert space is isometrically isomorphic to its dual space; if it's $\mathbb{C}$, then the Hilbert space is isometrically anti-isomorphic to the dual space.

Let $H$ be the Hilbert space, and $H^*$ denote its dual space, consisting of all continous linear functionals from $H$ into the field $\mathbb{R}$ or $\mathbb{C}$.

If $f \in H$, then the functional $\varphi_f$ is defined by:

\begin{equation*} \varphi_f(g) = \langle g, f \rangle, \quad \forall g \in H \end{equation*}

then $\varphi_f \in H^*$.

The Riesz representation theorem states that every element of $H^*$ can be written uniquely in this form.

Given any continuous functional $\psi_h \in H^*$, the corresponding element $h \in H$ can be constructed uniquely by

\begin{equation*} h = \psi_h(e_1) e_1 + \psi_h(e_2) e_2 + \dots \end{equation*}

where $\{ e_i \}$ is an orthonormal basis of $H$, and the value $h$ does not vary by choice of basis.

Theorem: The mapping $\Phi: H \to H^*$ defined by $\Phi(f) = \varphi_f$ is an isometric (anti-) isomorphism, meaning that:

  • $\Phi$ is bijective
  • The norms of $f$ and $\varphi_f$ agree: $||f|| = ||\Phi(f)||$
  • $\Phi$ is additive: $\Phi(f_1 + f_2) = \Phi(f_1) + \Phi(f_2)$
  • If the base field is $\mathbb{R}$, then $\Phi(\lambda f) = \lambda \Phi(f)$ for $\forall \lambda \in \mathbb{R}$
  • If the base field is $\mathbb{C}$, then $\Phi(\lambda f) = \bar{\lambda} \Phi(f)$ for $\forall \lambda \in \mathbb{C}$

In the mathematical treatment of quantum mechanics, the theorem can be seen as a justification for the popular bra-ket notation. The theorem says that, every bra $\bra{\psi}$ has a corresponding ket $\ket{\psi}$, and the latter is unique.

When we say the dual space is continuous we mean that the linear operator acting on the functions (elements) in the Hilbert space

If $\xi: \mathbf{H} \to \mathbb{C}$ is a bounded linear functional, then there exists a unique $\chi \in \mathbf{H}$ such that

\begin{equation*} \xi(\psi) = \left\langle \chi, \psi \right\rangle, \quad \forall \psi \in \mathbf{H} \end{equation*}

Furthermore, the operator norm of $\xi$ as a linear functional is equal to the norm of $\chi$ as an element of $\mathbf{H}$.

The operator norm is defined as

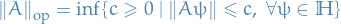
\begin{equation*} \norm{A}_{\text{op}} = \inf \left\{ c \ge 0 \mid \norm{A \psi} \le c, \ \forall \psi \in \mathbb{H} \right\} \end{equation*}

Mercer's Theorem

Let $K: [a, b]^2 \to \mathbb{R}$ be a symmetric continuous function, often called a kernel.

$K$ is said to be non-negative definite (or positive semi-definite) if and only if

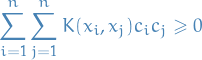
\begin{equation*} \sum_{i=1}^{n} \sum_{j=1}^{n} K(x_i, x_j) c_i c_j \ge 0 \end{equation*}

for all fininte sequences of points $x_1, \dots, x_n \in [a, b]$ and all choices of real numbers $c_1, \dots, c_n$.

We associate with $K$ a linear operator $T_K: L^2([a, b]) \to L^2([a, b])$ by

\begin{equation*} \big( T_K \varphi \big) (x) = \int_{a}^{b} K(x, s) \varphi(s) \ ds, \quad \varpih \in L^2([a, b]) \end{equation*}

The theorem then states that there is an orthonormal basis $\{ e_i \}$ of $L^2([a, b])$ consisting for eigenfunctions of $T_K$ such that the corresponding sequence of eigenvalues $\{ \lambda_i \}$ is nonnegative.

The eigenfunctions corresponding to non-zero eigenvalues are continuous on $[,a b]$ and $K$ has the representation

\begin{equation*} K(s, t) = \sum_{j=1}^{\infty} \lambda_j e_j(s) e_j(t) \end{equation*}

where the convergence is absolute and uniform.

There are alos more general versions of Mercer's thm which establishes the same result for measurable kernels, i.e. $K \in L_{\mu \otimes \mu}^2(X \times X)$ on any compact Hausdorff space $X$.

Generalized functions / distributions

Notation

  • $\mathbb{V}$ be a vector space over $\mathbb{R}$ and $\mathbb{V}^*$ be its dual space
  • $\mathcal{D}$ be the vector space $\mathcal{C}_0^{\infty}$ of functions $\varphi: \mathbb{R} \to \mathbb{R}$ with compact support which are infinitely differentiable

Stuff

  • 'singular functions' occur as a rule only in intermediate stages of solut

  • Given a 'singular function' we know the result of its integration against a "good" function $\varphi$:

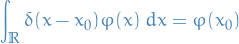
    \begin{equation*} \int_{\mathbb{R}}^{} \delta(x - x_0) \varphi(x) \ dx = \varphi(x_0) \end{equation*}

We say the sequence $\big( \varphi_n \big)$ with $\varphi_n \in \mathcal{D}$ converges to zero if

\begin{equation*} \varphi_n(x) = 0, \quad \forall x \notin I = [a, b], \forall n \in \mathbb{N} \end{equation*}

i.e. $\varphi_n$ has bounded support, and $\varphi_n$ and its derivatives converges uniformly to zero.

We say that the linear function $L \in \mathcal{D}^*$ is continuous if

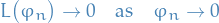
\begin{equation*} L \big( \varphi_n \big) \to 0 \quad \text{as} \quad \varphi_n \to 0 \end{equation*}

The set of continuous linear functionals is denoted $\mathcal{D}'$ and its elements are called distributions or generalized functions.

An example is the Dirac delta function $\delta: \mathcal{D} \to \mathbb{R}$ defined by

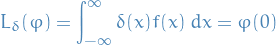
\begin{equation*} L_{\delta}(\varphi) = \int_{-\infty}^{\infty} \delta(x) f(x) \ dx = \varphi(0) \end{equation*}

We can then define scalar multiplication over 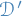$\mathcal{D}'$ by functions $f \in \mathcal{C}^{\infty}$, then if $L \in \mathcal{D}$ and $\varphi \in \mathcal{D}$, then

\begin{equation*} f L(\varphi) = L(f \varphi) \end{equation*}

Since we can add distributions, we can construct linear combinations

\begin{equation*} f_1 L_1 + f_2 L_2 + \dots + f_k L_k \end{equation*}

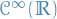of distributions with coefficients in the ring of $\mathcal{C}^{\infty}$ functions. Hence we have a module over $\mathcal{C}^{\infty}(\mathbb{R})$!