Graph Theory
Table of Contents
Notation
 denotes set of vertices in graph
denotes set of vertices in graph  (
( is used when there is no scope for ambiguity)
is used when there is no scope for ambiguity) denotes set of edges in graph
denotes set of edges in graph  (
( is used when there is no scope for ambiguity)
is used when there is no scope for ambiguity) and
and  denotes # of vertices and edges, respectively, unless stated otherwise
denotes # of vertices and edges, respectively, unless stated otherwise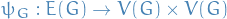 denotes the incidence function which maps an edge to the set of vertices connected by this edge
denotes the incidence function which maps an edge to the set of vertices connected by this edge denotes the set of neigbours of a vertex
denotes the set of neigbours of a vertex 
- A set
 , together with a set
, together with a set  of two-element subsets of
of two-element subsets of  , defines a simple graph
, defines a simple graph 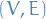 , where the ends of an edge
, where the ends of an edge  are precisely the vertices
are precisely the vertices 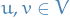
- incident matrix is
 matrix
matrix  , where
, where  is # of times (0, 1, or 2) that vertex
is # of times (0, 1, or 2) that vertex  and egde
and egde  are incident
are incident - adjacency matrix is
 matrix
matrix  , where
, where  is # of edges joining
is # of edges joining  and
and  , with each loop counting as two edges
, with each loop counting as two edges - biparite adjaceny matrix of some biparite graph
![$G[X, Y]$](../../assets/latex/graph_theory_211101297abe6b757cad43363e18504619392036.png) is the
is the  matrix
matrix  , where
, where  is # of edges joining
is # of edges joining  and
and 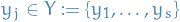
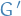 denotes a sub-graph of some graph
denotes a sub-graph of some graph  , i.e.
, i.e.  (unless otherwise specified)
(unless otherwise specified)
Definitions
Terminology
We say a graph  is densily connected at vertex
is densily connected at vertex  if
if  is "large".
is "large".
If we have a cluster of such vertices, we might refer to this cluster as being assortative ; in contrast we refer to clusters of vertices which connect similarily to the rest of the graph (vertices "outside" of the cluster) without necessarily having higher inner density, as disassortative communities / clusters.
General
A tree is a undirected graph in which any two vertices are connected by exactly one path.
E.g. a acyclic connected graph is a tree.
Sometimes a tree also has the additional constraint that every node has at most a single parent, and polytrees refer to what we just defined.
A spanning tree  of an undirected graph
of an undirected graph  is a subgraph that is a tree which includes all of the vertices of
is a subgraph that is a tree which includes all of the vertices of  , with miniumum possible number of edges.
, with miniumum possible number of edges.
In general, a graph may have several spanning trees, but a graph that is not connected will not contain a spanning tree.
If all of the edges of  are also edges of a spanning tree
are also edges of a spanning tree  of
of  , then
, then  is a tree and is identical to
is a tree and is identical to  (i.e. a tree has a unique spanning tree and it's itself).
(i.e. a tree has a unique spanning tree and it's itself).
A cut is a partition of a the vertices of a graph into two disjoint subsets.
Any cut determines a cut-set, that is the set of edges which have one endpoint in each subset of the partition.
A simple graph is a graph where both multiple edges and self-loops are dissallowed.
Thus, in a simple graph with  vertices, each vertex is at most of degree
vertices, each vertex is at most of degree 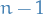 .
.
Let  and
and  be two graphs.
be two graphs.
Graph 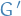 is a sub-graph of
is a sub-graph of  , written
, written  , if
, if

If  contains all of the edges
contains all of the edges  with
with  , then
, then 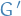 is an induced sub-graph of
is an induced sub-graph of  .
.
When  and there exists an isomorphism between the sub-graph
and there exists an isomorphism between the sub-graph 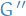 and a graph
and a graph 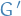 , this mapping represents an appearance of
, this mapping represents an appearance of 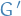 in
in  .
.
A graph is called recurrent or frequent in  , when its frequency
, when its frequency  is aboe a predefined threshold or cut-off value.
is aboe a predefined threshold or cut-off value.
Intersection graph
An intersection graph is a graph that represents the pattern of intersections of a family of sets.
Formally, an intersection graph is an undirected graph formed from a family of sets

by creating one vertex  for each set
for each set  , and connecting two vertices
, and connecting two vertices  and
and 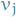 by an edge whenever the corresponding two sets have a nonempty intersection, i.e.
by an edge whenever the corresponding two sets have a nonempty intersection, i.e.
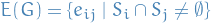
Chordal graph
A chordal graph is one in which all cycles of 4 or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle.
Sometimes these are referred to as triangulated graphs.
Network motifs
Network motifs are defined as recurrent and statistically significant sub-graphs or patterns in a graph.
There is an ensemble 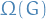 of random graphs corresponding to the null-model associated to
of random graphs corresponding to the null-model associated to  . We should choose
. We should choose  random graphs uniformly from
random graphs uniformly from 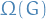 and calculate the frequency for a particular frequent sub-graph
and calculate the frequency for a particular frequent sub-graph 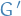 in
in  .
.
If the frequency of 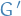 in
in  is higher than its arithmetic mean frequency in
is higher than its arithmetic mean frequency in  random graphs
random graphs 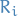 , we acll this recurrent pattern significant and hence treat
, we acll this recurrent pattern significant and hence treat 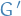 as a network motif for
as a network motif for  .
.
For a small graph 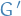 , the network
, the network  and a set of randomized networks
and a set of randomized networks  wher
wher  , the z-score of
, the z-score of 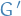 is defined as:
is defined as:

where  and
and  stand for mean and std. dev. frequency in set
stand for mean and std. dev. frequency in set  respectively.
respectively.
The larger the  , the more significant is the sub-graph
, the more significant is the sub-graph 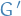 as a motif.
as a motif.
Clique
A clique is defined as a subset of nodes in a graph such that there exists a link between all pairs of nodes in the subset.
In other words, a clique is fully connected.
A maximal clique is a clique such that it is not possible to include any other nodes from the graph in the set without it ceasing to be a clique.
Theorems
Book: Graph Theory
1. Graphs
Notation
 denotes set of vertices in graph
denotes set of vertices in graph  (
( is used when there is no scope for ambiguity)
is used when there is no scope for ambiguity) denotes set of edges in graph
denotes set of edges in graph  (
( is used when there is no scope for ambiguity)
is used when there is no scope for ambiguity) and
and  denotes # of vertices and edges, respectively, unless stated otherwise
denotes # of vertices and edges, respectively, unless stated otherwise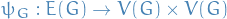 denotes the incidence function which maps an edge to the set of vertices connected by this edge
denotes the incidence function which maps an edge to the set of vertices connected by this edge denotes the set of neigbours of a vertex
denotes the set of neigbours of a vertex 
- A set
 , together with a set
, together with a set  of two-element subsets of
of two-element subsets of  , defines a simple graph
, defines a simple graph 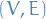 , where the ends of an edge
, where the ends of an edge  are precisely the vertices
are precisely the vertices 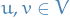
- incident matrix is
 matrix
matrix  , where
, where  is # of times (0, 1, or 2) that vertex
is # of times (0, 1, or 2) that vertex  and egde
and egde  are incident
are incident - adjacency matrix is
 matrix
matrix  , where
, where  is # of edges joining
is # of edges joining  and
and  , with each loop counting as two edges
, with each loop counting as two edges - biparite adjaceny matrix of some biparite graph
![$G[X, Y]$](../../assets/latex/graph_theory_211101297abe6b757cad43363e18504619392036.png) is the
is the  matrix
matrix  , where
, where  is # of edges joining
is # of edges joining  and
and 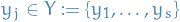
 denotes the degree of
denotes the degree of  , i.e. # of edges incident with
, i.e. # of edges incident with  , each loop counting as two edges
, each loop counting as two edges and
and  are the minimum and maximum degrees of the vertices of
are the minimum and maximum degrees of the vertices of 
 is the average degree of the vertices of
is the average degree of the vertices of 
1.1 Graphs and Their Representations
A graph is an ordered pair  consisting of a set
consisting of a set  of vertices and a set
of vertices and a set  , disjoint from
, disjoint from  , of edges, together with an incidence function
, of edges, together with an incidence function  that associates with each edge of
that associates with each edge of  an unordered pair of vertices of
an unordered pair of vertices of  .
.
If  is an edge and
is an edge and  and
and  are vertices such that
are vertices such that  .
.
A biparite graph is a simple graph where the vertices  can be partitioned into two subsets
can be partitioned into two subsets  and
and  such that every edge has one end in
such that every edge has one end in  and one end in
and one end in  ; such a partition
; such a partition 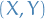 is called a bipartition of the graph, and
is called a bipartition of the graph, and  and
and  its parts.
its parts.
A path is a simple graph whose vertices can be arranged in a linear sequence s.t. two vertices are adjacent if they are consecutive in the sequence, and are non-adjacent otherwise.
A cycle on three or more vertices in a simple graph whose vertices can be arranged in a cyclic sequence s.t. two vertices are adjacent if they are consecutive in the sequence, and are non-adjacent otherwise.
A graph is connected if and only if for every partition of its vertex set into two nonempty sets  and
and  , there is an edge with one end in
, there is an edge with one end in  and one end in
and one end in  ; otherwise the graph is disconnected.
; otherwise the graph is disconnected.
Equivalently, if there is a u-v-path in  (a path fro m
(a path fro m  to
to  ) for every pair of vertices
) for every pair of vertices  .
.
A graph  is k-regular if
is k-regular if
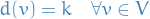
A regular graph is one that is k-regular for some  .
.
Counting in two ways is a proof-technique where we consider a suitable matrix and compute the sum of its entries in two different ways:
- sum of its row sums
- sum of its column sums
Equating these two quantities results in an identity.
Exercises
- 1.1.5
- Question
For
 , characterize the k-regular graphs.
, characterize the k-regular graphs.
- Answer
Let
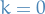 , i.e.
, i.e.

which is simply a graph without any connections between the vertices.
For
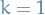 , we have
, we have
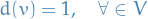
For any
 we then the following possibilities:
we then the following possibilities:
- connected to itself, thus not connected to any other vertices, which in turn implies that we can consider two graphs;
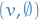 and
and 
- connected to another single vertex
 : a simple sequence of vertices, i.e. a path, since each vertex is connected only to one other
: a simple sequence of vertices, i.e. a path, since each vertex is connected only to one other
In total, a 1-regular graph can be separeted into graphs consisting of a single vertex with no edges (for all the vertices connected by loops) and a single graph which is a path.
For
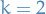 , we have
, we have
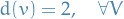
For any
 we then have the following possibilities:
we then have the following possibilities:
- both edges are loops: we can consider two graphs;
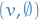 and
and 
- both edges are not loops: here we can have two cases
 is part of a cycle
is part of a cycle  : can consider two separate graphs
: can consider two separate graphs  and
and  , since every
, since every  is connected to two other vertices in
is connected to two other vertices in 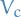 for
for  to form a cycle.
to form a cycle.  is then simply a polygon
is then simply a polygon is not a part of a cycle: we have a simple graph
is not a part of a cycle: we have a simple graph
one edge is loop, one edge is non-loop:
 can then only be connected to a single
can then only be connected to a single  which also has one loop and one non-loop, thus they form:
which also has one loop and one non-loop, thus they form:
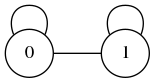
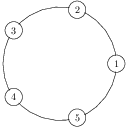
All in all, we can separate a 2-regular graph into graphs of the following classification:
- empty graphs
- k-cycles
- graphs of the form 1
- connected to itself, thus not connected to any other vertices, which in turn implies that we can consider two graphs;
- Question
Terminology
- loop
- edge with identical ends
- link
- edge with distinct ends
- parallel edges
- two or more links with the same pair of ends
- null graph
- graph with zero vertices
- trivial graph
- graph with one vertex
- complete graph
- simple graph in which any two vertices are adjacent
- empty graph
- simple graph in which no two vertices are adjacent, i.e.
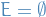
- k-path
- path of length

- k-cycle
- cycle of length

- planar graph
- graph which can be drawn in a plane (2D) s.t. edges meet only at points corresponding to their common ends, i.e. no intersections when drawn in a 2D plane, where the drawing itself is called a planar embedding
- embedding
- "drawing" of a graph on some n-dimensional structure so that its edges intersect only at their ends
Book: Bayesian Reasoning and Machine Learning
Notation
 denotes the parent nodes of the rv.
denotes the parent nodes of the rv.  in the BN
in the BN
7. Making Decisions
Notation
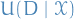 denotes the expected utility of decision
denotes the expected utility of decision  over the set of rvs.
over the set of rvs. 
7.3 Extending Bayesian Networks for Decisions
An Influence Diagram (ID) states which information is required in order to make each decision, and the order in which these decisions are to be made.
We call an information link fundamental if its removal would alter the partial ordering.
7.4 Solving Influence Diagrams
A decision potential on a clique  contains two potentials: a probability potential
contains two potentials: a probability potential 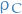 and a utility potential
and a utility potential  . The join potentials for the junction tree are defined as
. The join potentials for the junction tree are defined as
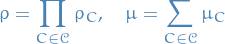
with the junction tree representing the term  .
.
But for IDs there are constraints on the triangulation since we need to preserve the partial ordering induced by the decisions, which gives rise to strong Junction Tree.
- Remove information edges
- Moralization: marry all parents of the remaining nodes
- Remove utility nodes: remove the utility nodes and their parental links
- Strong triangulation: form a triangulation based on an elimination order which obeys the partial ordering of the variables.
- Strong Junction Tree: From the strongly triangulated graph, form a junction tree and orient the edges towards the strong root (the clique that appears last in the eliminiation sequence).
Spectral Clustering
Notation
 denotes the i-th vertex
denotes the i-th vertex when
when  is adjacent to
is adjacent to 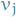
 denotes the edge between
denotes the edge between  and
and 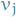
- Edges are non-negatively weighted with the weight matrix
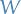
 is the diagonal matrix of
is the diagonal matrix of 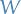 , also called the degree matrix, defined as:
, also called the degree matrix, defined as:
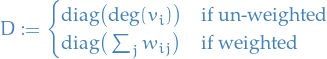
 denotes the unnormalized graph Laplacian
denotes the unnormalized graph Laplacian denotes the normalized graph Laplacian
denotes the normalized graph Laplacian
Stuff
- Want to partition a graph in parts which are roughly the same size and are connected by as few edges as possible, or informally, "as disjoint as possible"
- NP-hard (even approximations are difficult)
- Good heuristic: write cost function as a quadratic form and relaxing the discrete optimization problem of finding the characteristic function of the cut to a real-valued optimization problem
- Leads to an eigenproblem
The volume of a subset of vertices  is the total degree of all vertices in the subset:
is the total degree of all vertices in the subset:

If  is a set of vertices of
is a set of vertices of  , we define it's edge boundary
, we define it's edge boundary  to be the set of edges connecting
to be the set of edges connecting  and its complement
and its complement  .
.
Similiarily, the volume of  is defined as
is defined as

The minimum cut of a graph  refers to the partition
refers to the partition 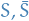 which minimizes
which minimizes  , i.e. the smallest total weight "crossing" between the partitions
, i.e. the smallest total weight "crossing" between the partitions  and
and  .
.
Problem with mincut is that no penalty is paid for unbalanced partitions and therefore nothing prevents the algorithm from making single vertices "clusters".
The Cheeger constant (minimum conductance) of a cut is defined

The normalized cut is defined as

For 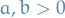 ,
,
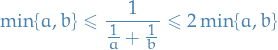
from which we can see that Cheeger constant and normalized cut are closely related.
Both are NP-hard, thus need to be approximated.
The weighted and unweighted , respectively, balanced cuts of a graph are given:
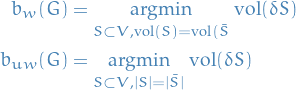
We'll assume balanced partitions exists (e.g. for unweighted version the number of vertices has to be even). For the general case one can easily modify the definition requiring the partition to be "almost balanced", and this will lead to the same relaxed optimization problems in the end.
The unnormalized graph Laplacian is defined to be

and the normalized graph Laplacian
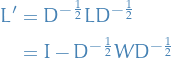
From  and
and  various graph invariants can be estimated in terms of eigenvalues of these matrices.
various graph invariants can be estimated in terms of eigenvalues of these matrices.
Given a vector  , we have the following identity:
, we have the following identity:

thus  is positive semi-definite, and since
is positive semi-definite, and since  is positive definite the same holds for
is positive definite the same holds for  .
.
Spectral clustering
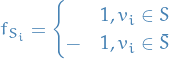
Given a subset  , define the column vector
, define the column vector  as follows:
as follows:
Then it's immediate that
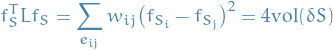
since  and
and  .
For all
.
For all  we have
we have

Consider the weighted balanced cut:

Hence, 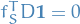 if and only if the cut corresponding to
if and only if the cut corresponding to  is volume-balanced, i.e.
is volume-balanced, i.e.

Therefore, we can reformulate the problem of computing weighted balanced cut as:
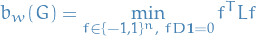
Moreover, as  has constant value
has constant value  for all
for all  , we can rewrite this as
, we can rewrite this as

I'll be honest and say I do not see where this  comes from.
comes from.
In this form, the discrete optimization problem admits a simple relaxation by letting  instead of
instead of  . Noticing that
. Noticing that
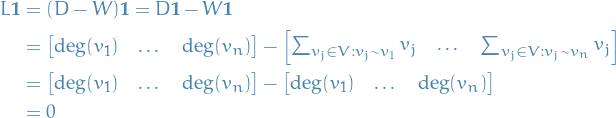
a standard linear algebra argument shows that
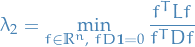
I tried to figure out why "since 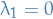 the minimizer is instead
the minimizer is instead 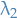 !" and what I can gather is that:
!" and what I can gather is that:
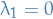 means that the matrix is non-invertible
means that the matrix is non-invertible- Then only consider
 , i.e. subspace not spanned by eigenspace of
, i.e. subspace not spanned by eigenspace of 
- Left with this stuff, which makes sense; the Rayleigh quotient is minimized by the first eigenvalue
where 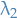 is the second smallest eigenvalue of the generalized eigenvector problem
is the second smallest eigenvalue of the generalized eigenvector problem  . It is clear that the smallest eigenvalue
. It is clear that the smallest eigenvalue  of
of  is
is  (since
(since  as noted earlier) and the corresponding eigenvector is
as noted earlier) and the corresponding eigenvector is  .
.
Further, we can show that for a connected graph,  . Thus, the vector
. Thus, the vector  for which the minimum above is attained is the eigenvector corresponding to
for which the minimum above is attained is the eigenvector corresponding to 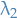 .
.
This leads directly to the bipartitioning algortihm as relaxation of the weighted balanced cut:
- Compute the matrices
 and
and 
Find the eigenvector corresponding to the second smallest eigenvalue of the following generalized eigenvalue problem:

Obtain the partition:

where  denotes the i-th entry of the corresponding eigenvector.
denotes the i-th entry of the corresponding eigenvector.
For unnormalized spectral clustering, a similar argument shows that

and by relaxation we obtain an identical algorithm, except taht the eigenproblem

is sovled instead.
Network Data Analysis
Notation
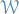 denotes the linear space of all bounded symmetric measureable functions
denotes the linear space of all bounded symmetric measureable functions ![$[0, 1]^2 \to \mathbb{R}$](../../assets/latex/graph_theory_1a5f286271bacf248c029cc3cc6646edcfd01f21.png)
 is a kernel:
is a kernel:
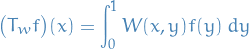
Considered as an operator
![$L_\infty[0, 1] \to L_1[0, 1]$](../../assets/latex/graph_theory_94410d9c0fef82e4ecafd3767ec5240ccc8a2f83.png)
![\begin{equation*}
\norm{T_W}_{\infty \to 1} = \sup_{f \in L_{\infty}[0, 1]: \norm{f}_\infty = 1} \norm{T_w f}_1
\end{equation*}](../../assets/latex/graph_theory_0c63778380a9f823acb9bd2a21ac86b346fb1563.png)
 is used to control sparsity
is used to control sparsity is the
is the is the expected number of occurences of subgraph
is the expected number of occurences of subgraph  in graph
in graph 
- "random graph" = Erdos-Renyi
Stuff
- Treating adjacency-matrix as a multi-dimensional Bernoulli rv. => allows possibility "construction" and "destruction" of connections
Real networks often follow:
Limiting behaviour

- Heterogenous:
 for some choices of
for some choices of  or
or  and
and 
- No ordering
Hence, we consider the limiting behaviour
Graphons
A graphon is a symmetric measurable function ![$W: [0, 1]^2 \to [0, 1]$](../../assets/latex/graph_theory_ad939bc735caf4be8f9ef148566ab85cd762e055.png) .
.
Usually a graphon is understood as defining an exchangeable random graph model according to the following scheme:
- Each vertex
 of the graph is assigned an independent random value
of the graph is assigned an independent random value ![$u_j \sim U[0, 1]$](../../assets/latex/graph_theory_a3f407755cc9e2c71572c9f7fbfca7f6d4611c2e.png)
- Edge
 is independently included in the graph with probability
is independently included in the graph with probability 
A random graph model is an exchangeable random graph model if and only if can be defined in terms of a (possibly random) graphon in this way.
It is an immediate consequence of this definition and the law of large numbers that, if  , exchangeable random graph models are dense almost surely.
, exchangeable random graph models are dense almost surely.
Define a generative model of random graphs
- Fix a nonegative kernel
 and scale
and scale 
- Generate iid Uniform(0, 1) variates

- Indep. connect vertices
 w.p.
w.p. 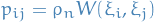
Can we recover  up to scale from an observed graph?
up to scale from an observed graph?
We therefore consider the cut distance, which can be defined naturally on the linera space  of kernels.
of kernels.
Constructing an exchangeable model
Suppose we give 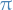 a univariate "prior" distribution
a univariate "prior" distribution
eqn scale the resulting mean matrix  by
by  to control sparsity:
to control sparsity:
![\begin{equation*}
\mathbb{E}[A_{ij} \mid \pi ] = p_{ij} = \rho_n \cdot \pi_i \pi_j
\end{equation*}](../../assets/latex/graph_theory_fc2d992cdcecf69dfde666c3e0f220a41cdb6456.png)
Let  , then
, then
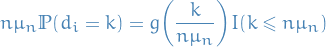
where  is a "Kartauff effect" (?)
is a "Kartauff effect" (?)
Stochastic block models
Assume each node is assigned categorical variable 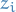 :
:
![\begin{equation*}
\mathbb{E}[A_{ij} \mid z] = \theta_{ab} I(z_i = a) I(z_j = b)
\end{equation*}](../../assets/latex/graph_theory_05e13f0e5075965238b917f7216748a9bd1db15b.png)
The a-th fitted community then comprises  > 1 nodes:
> 1 nodes:
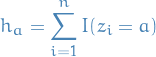
i.e.  is the number of members in the community.
is the number of members in the community.
These "bandwiths" define a CDF  an its inverse
an its inverse  .
.
Any community assignment function  has two components:
has two components:
- A vector
 of community sizes (defines
of community sizes (defines  )
) - A permutation
 of
of  that re-orders the nodes prior to applying the quantile function
that re-orders the nodes prior to applying the quantile function  .
.
Community to which  assigns node
assigns node  is determined by the composition
is determined by the composition  :
:

Thus, each  represents a re-ordering of the network nodes, followed by a partitioning of the unit interval.
represents a re-ordering of the network nodes, followed by a partitioning of the unit interval.
Comparing features
- Inexact graph matching - maximum common subgraph, etc.
- Edit distance - convergence implies that motif prevalences converge also
- Motif prevelance
One way
Count prevalance of subgraph
 in graph
in graph 
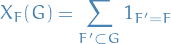
- Compare to a null-model, typically moment matched (i.e. matching something like mean, variance, etc.)
- Compare subgraphs
 somehow
somehow - Finite connected graph
 can be mapped out by a closed walk
can be mapped out by a closed walk  (i.e. sequence of vertices)
(i.e. sequence of vertices) - Walks in a network determine its classification as a topological space
- Euler characteristic:

- Number of closed k-walks in
 derives from its adjancey matrix:
derives from its adjancey matrix: 
- For large classes of networks, walks mapping out maximal trees and cycles dominate => allows comparison between "random graphs"
- Turns out that counting cycles allows one to determine whether or not we're just looking at a "random graph"; i.e. if the graph exhibits any interesting behavior or not
Tree decomposition
- Also called juntion trees, clique trees or join trees
Moralization of a graph is the process of turning a directed graph into an undirected graph by "marrying" of parent nodes.
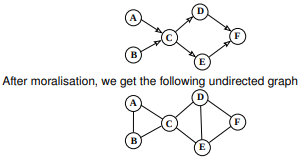
Figure 3: Source http://www.inf.ed.ac.uk/teaching/courses/pmr/slides/jta-2x2.pdf
Triangulation refers to the process of turning a graph into a chordal graph.
One of the reasons why this is so useful is when we turn triangulated graph into a clique tree for use in representing a factor graph.
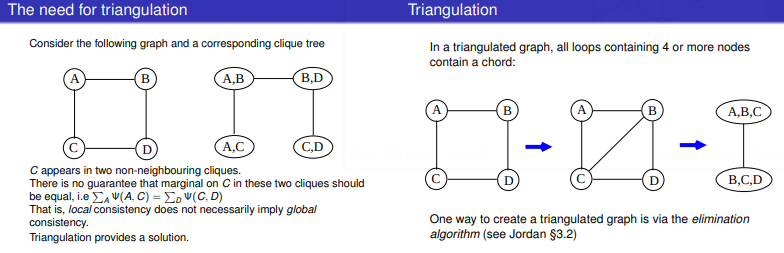
Figure 4: Source http://www.inf.ed.ac.uk/teaching/courses/pmr/slides/jta-2x2.pdf
A junction tree or tree decomposition represents the vertices  of a given graph
of a given graph  as subtrees of a tree, in such a way that the vertices in the given graph are adjacent only when the corresponding subtrees intersect.
as subtrees of a tree, in such a way that the vertices in the given graph are adjacent only when the corresponding subtrees intersect.
Thus,  forms a subgraph of the intersection graph of the subtrees. The full intersection graph is a chordal graph.
forms a subgraph of the intersection graph of the subtrees. The full intersection graph is a chordal graph.
Given a graph  , a junction tree is a pair
, a junction tree is a pair 
 where
where  (in some literature referred to as "supernodes")
(in some literature referred to as "supernodes")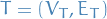 is a tree whose nodes correspond to the subsets
is a tree whose nodes correspond to the subsets  , i.e. a vertex
, i.e. a vertex  is defined by
is defined by 
And this pair  is required to satisfy the following:
is required to satisfy the following:
 , i.e. each vertex is associated with at least one tree node in
, i.e. each vertex is associated with at least one tree node in 
Vertices are adjacent in the graph
 if and only if the corresponding subtrees have a node in common, i.e.
if and only if the corresponding subtrees have a node in common, i.e.

If
 and
and  both contain a vertex
both contain a vertex  , then all nodes
, then all nodes 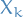 of the tree in (unique) path between
of the tree in (unique) path between 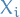 and
and  contain
contain  as well, i.e.
as well, i.e.

where
 denotes the set of notes in the (unique) path between
denotes the set of notes in the (unique) path between 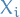 and
and 
A junction tree is not unique, i.e. there exists multiple ways to perform a decomposition described above.
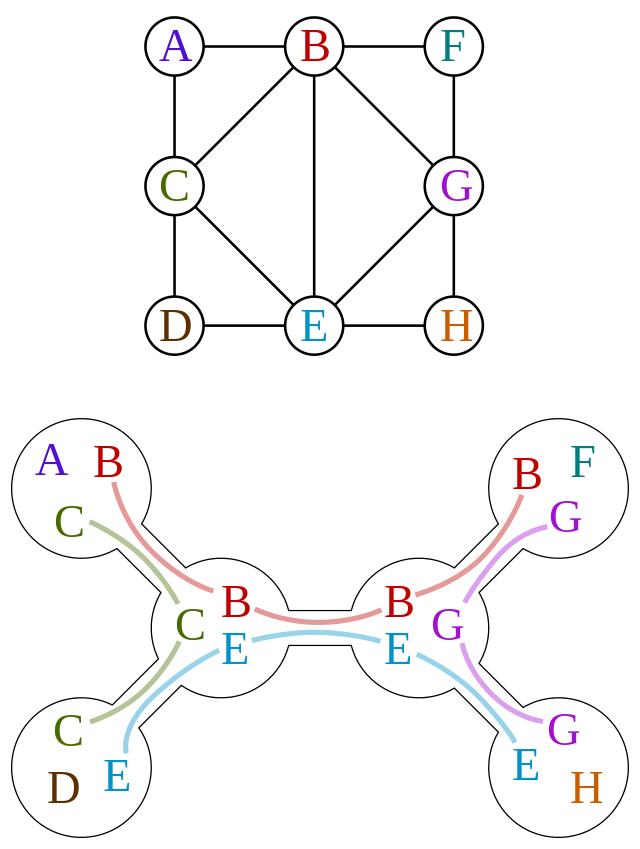
Figure 5: 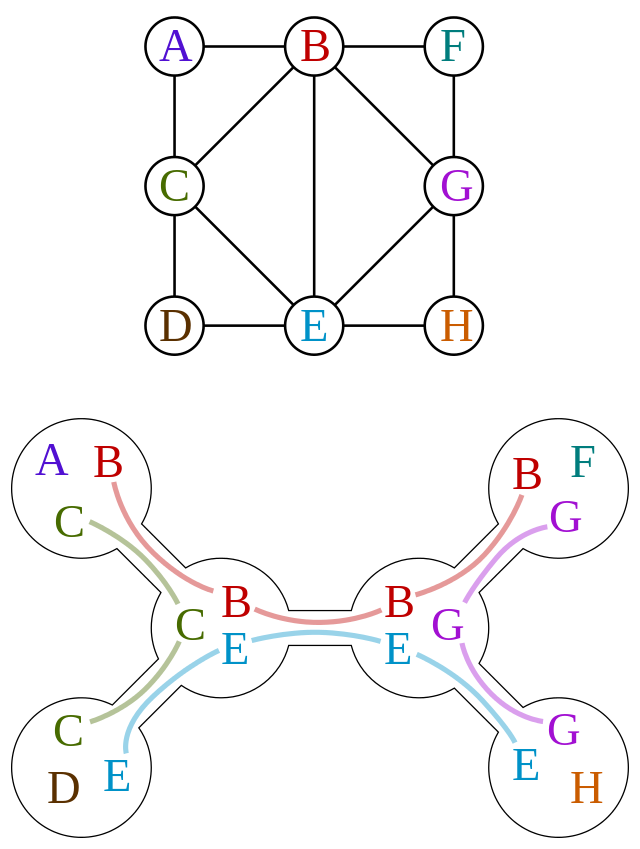
Often you'll see that it's suggested to transform a graph into a chordal graph before attempting to decompose it.
This is due to a theorem which states that the following two are equivalent:
 is triangulated
is triangulated- Clique graph of
 has a junction tree
has a junction tree
One method of exact marginalization in general graphs is called the junction tree algorithm, which is simply belief propagation on a modified graph guaranteed to be a tree.
The basic premise is to eliminate cycles by clustering them into single nodes.
Given a triangulated graph, weight the edges of the clique graph by their cardinality,  , of the intersection of the adjacent cliques
, of the intersection of the adjacent cliques 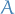 and
and  . Then any maximum-weight spanning tree of the clique graph is a junction tree.
. Then any maximum-weight spanning tree of the clique graph is a junction tree.
Thus, to construct a junction tree, we just have to extract a maximum weight spanning tree out of the clique graph.
A width of a tree decomposition is the size of its largest set 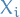 minus one, i.e.
minus one, i.e.

And the treewidth 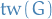 of a graph
of a graph  is the minimum width among all possible tree decompositions of
is the minimum width among all possible tree decompositions of  , i.e.
, i.e.

Stochastic Block Modelling
Notation
 number of vertices, thus
number of vertices, thus ![$v \in [n]$](../../assets/latex/graph_theory_572b16d3a3e596a52b9f6077873ea0d7dff2be40.png)
 number of communities
number of communities n-dimensional random vector with i.i.d. components distributed under
n-dimensional random vector with i.i.d. components distributed under 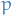 , i.e. representing the community-assignment of each vertex
, i.e. representing the community-assignment of each vertex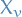 is the random variable representing the community of which vertex
is the random variable representing the community of which vertex  belongs to, taking on values in
belongs to, taking on values in ![$[k]$](../../assets/latex/graph_theory_a46760c00adda23a3fc4c4a47e402dee24e8aaad.png) , i.e.
, i.e. 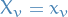 with
with ![$x_v \in [k]$](../../assets/latex/graph_theory_a41b7d71f26a7fe7621f13b84e696f72cfea1448.png)
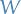 is a
is a  symmetric matrix with vertices
symmetric matrix with vertices  and
and  being connected with probability
being connected with probability  , indep. of other pairs of vertices.
, indep. of other pairs of vertices.![$\Omega_i = \Omega_i(X) := \{ v \in [n] \mid X_v = i, i \in [k] \}$](../../assets/latex/graph_theory_88a31b74931296af74a1720cf551c073a7d60381.png) denotes a community set
denotes a community set denotes a community-graph pair
denotes a community-graph pair
Stuff

- Probability vector
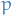 of dimension
of dimension 
- Symmetric matrix
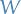 of dimension
of dimension  with entries in
with entries in ![$[0, 1]$](../../assets/latex/graph_theory_68c8fa38d960e53d4308cbf1e65d04c66a554817.png)
Then  defines a n-vertex random graph with labelled vertices, where each vertex is assigned a community label in
defines a n-vertex random graph with labelled vertices, where each vertex is assigned a community label in  independently under the community prior
independently under the community prior 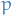 , and pairs of vertices with labels
, and pairs of vertices with labels  and
and  connect independently with probability
connect independently with probability 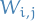 .
.
Further generalizations allow for labelled edges and continuous vertex labels, conencting to low-rank approximation models and graphons.
Thus the distribution of  where
where ![$G = \big( [n], E(G) \big)$](../../assets/latex/graph_theory_42bccc68275c40f74ab2fd71732bbda541b790e6.png) is
is
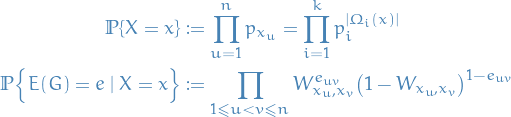
which is just saying:
![\begin{equation*}
\begin{split}
X_u & \sim \text{Multinomial}(k), \quad \forall u \in [n] \\
E_{uv} & \sim \text{Bernoulli}(W_{x_u, x_v}), \quad \forall u, v \in [n], u \ne v
\end{split}
\end{equation*}](../../assets/latex/graph_theory_090207e24f83667a116fe6e96d61c2e989ad2e06.png)
Graphical models
Min-Max propagation
Algorithms
Shortest path
Dijkstra's Shortest Path
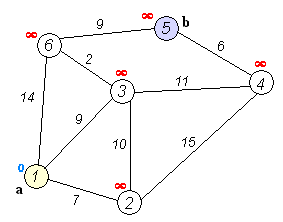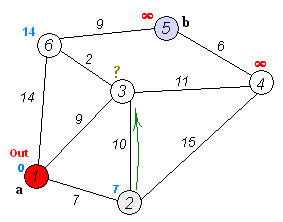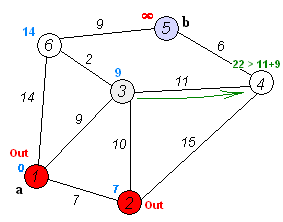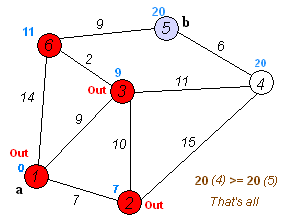
And here's a super-inefficient implementation of Djikstra's shortest path algorithm in Python:
import numpy as np from collections import defaultdict, deque, namedtuple def is_empty(q): return len(q) < 1 def get_neighbors(v, graph): neighs = [] for e in graph.edges: if e.vertices[0] == v: neighs.append((e, e.vertices[1])) elif e.vertices[1] == v: neighs.append((e, e.vertices[0])) return neighs # structures Node = namedtuple('Node', ['value']) Edge = namedtuple('Edge', ['vertices', 'weight', 'directed']) Graph = namedtuple('Graph', ['vertices', 'edges']) # straight foward problem V = [Node(i) for i in range(10)] E = [Edge([V[i - 1], V[i]], i, False) for i in range(1, 9)] + [Edge([V[8], V[9]], 0, False)] G = Graph(V, E) # shortcut! E = E + [Edge([V[4], V[8]], -6, False)] G = Graph(V, E) v_0 = V[0] # start v_n = V[-1] # stop paths = {} path_weights = defaultdict(lambda: np.inf) seen = set() queue = deque([v_0, v_n]) seen.add(v_n) v_curr = queue.popleft() path_weights[v_curr] = 0 # initialize path weight to 0 from starting point path_w = path_weights[v_curr] paths[v_curr] = None edge, v_neigh = get_neighbors(v_curr, G)[0] # update best prev vertex candidate for `v_neigh` paths[v_neigh] = v_curr # update best candidate weight path_weights[v_neigh] = edge.weight + path_w while not is_empty(queue) and v_curr != v_n: for (edge, v_neigh) in get_neighbors(v_curr, G): if v_neigh == paths[v_curr]: # if it's the neighboring vertex we just came from => skip it continue # proposed path is improvement over previous path with `v_neigh` ? candidate_path_weight = path_weights[v_neigh] if edge.weight + path_w < candidate_path_weight: # update best prev vertex candidate for `v_neigh` paths[v_neigh] = v_curr # update best candidate weight path_weights[v_neigh] = edge.weight + path_w if v_neigh not in seen: queue.append(v_neigh) seen.add(v_neigh) # sort `queue` so that the next visit is to the current "shortest" path queue = deque(sorted(queue, key=lambda v: path_weights[v])) v_curr = queue.popleft() path_w = path_weights[v_curr] # upon termination we simply walk backwards to get the shortest path optimal_path = [v_n] v_curr = v_n while v_curr != v_0: v_curr = paths[v_curr] optimal_path.append(v_curr) def display_path(path): print("Optimal path: " + " --> ".join([str(v.value) for v in path])) display_path(list(reversed(optimal_path))) print("Observe that some nodes are NEVER seen, as we'd like!") from pprint import pprint pprint(list(paths.keys()))
Optimal path: 0 --> 1 --> 2 --> 3 --> 4 --> 8 --> 9 Observe that some nodes are NEVER seen, as we'd like! [Node(value=0), Node(value=1), Node(value=2), Node(value=3), Node(value=4), Node(value=5), Node(value=8), Node(value=7), Node(value=9)]
#include <iostream> #include <memory> template<typename T> struct BinTreeNode { T value; std::shared_ptr<BinTreeNode<T>> left = nullptr; std::shared_ptr<BinTreeNode<T>> right = nullptr; BinTreeNode(T v) : value(v) { } }; int main() { std::shared_ptr<BinTreeNode<int>> root = std::shared_ptr<BinTreeNode<int>>(new BinTreeNode<int>(0)); root->left = std::make_shared<BinTreeNode<int>>(1); root->right = std::make_shared<BinTreeNode<int>>(2); root->left->left = std::make_shared<BinTreeNode<int>>(4); std::cout << root->value << std::endl; std::cout << root->left->value << std::endl; std::cout << root->left->left->value << std::endl; std::shared_ptr<BinTreeNode<int>> current = root; for (auto i = 0; i < 10; i++) { // using "raw" pointers, these `BinTreeNode` instances will live long enough // but risking dangling pointers in the case were we delete a parent node // UNLESS we specificly delete them (which we can do using a custom destructor for `BinTreeNode`) // Instead we can use `std::shared_ptr` which has an internal reference-counter, // deallocating only when there are no references to the object std::shared_ptr<BinTreeNode<int>> next = std::make_shared<BinTreeNode<int>>(i); std::cout << next->value << std::endl; if (next->value >= current->value) { current->right = next; } else { current->left = next; } current = next; } std::cout << root->right->right->value << std::endl; return 0; }
Bellman-Ford algorithm
- Computes shortest paths from single source vertex to all other vertices in a weighted digraph
- Slower than Dijkstra's Algorithm for same problem, but more versatile
- Capable of handling edges with negative weights
- Can be used to discover negative cycles (i.e. a cycle whose edges sum to a negative value)
- E.g. arbitrage opportunities on Forex markets
Relation to Dijkstra's algorithm:
- Both based on principle of relaxation:
- Approximation of the correct distance is gradually replaced by more accurate values until eventually reaching the optimum solution
- Approx. distnace to each vertex is an overestimate of true distance, and is replacted by the minimum of its old value and the length of the newly found path
- All nodes are initialized to be
 away from the source vertex
away from the source vertex 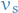 , i.e. an overestimate
, i.e. an overestimate - Update these distances at each iteration
- All nodes are initialized to be
- Difference:
- Dijkstra's: uses priority queue to greedily select the closest vertex that has not been processed, and performs this relaxation process on all of its outgoing edges
- BF: simply relaxes all the edges, and does this
 times (since there can be at most
times (since there can be at most  edges on a path between any two vertices)
edges on a path between any two vertices)
- Can terminate early if shortest paths does not change between two iterations
- In practive the ordering of which we update the edges can improve the runtime
Impl
def bellman_ford(vertices, edges, source):
distances = {source: 0.0}
previous = {}
# instead of using infinity as initial value, we simply
# check if the vertex is already in ``distances`` as a
# proxy for "infinity" distance. Hence we do not need an initialization.
# perform relaxation iterations
diff = True
i = 0
while diff and i < len(vertices) - 1:
diff = False
# iterate over vertices which are reachable
for v in (v for v in vertices if v in distances):
v_dist = distances[v]
outgoing_edges = [e for e in edges if e[0] == v]
for (_, u, w) in outgoing_edges:
if u not in distances or v_dist + w < distances[u]:
# found new shortert path to vertex ``u``
distances[u] = v_dist + w
previous[u] = v
# made a change
diff = True
# update counter
i += 1
return distances
# negative cycle
edges = [
(0, 1, 1.0),
(1, 2, 1.0),
(0, 2, 4.0),
(2, 3, 1.0),
(3, 0, -5.0)
]
vertices = [v for v in range(4)]
bellman_ford(vertices, edges, 0)
Conclusion
| Algorithm | Greedy | Negative edges? | Complexity | |
|---|---|---|---|---|
| Dijkstra | Y | N | ||
| Bellman-Ford | N | Y |  |
Code
graph-tool python
import graph_tool.all as gt g = gt.collection.data["football"] g
# Out[4]: : <Graph object, undirected, with 115 vertices and 613 edges at 0x7f25204da438>
state = gt.minimize_blockmodel_dl(g) state
# Out[6]: : <BlockState object with 10 blocks (10 nonempty), degree-corrected, for graph <Graph object, undirected, with 115 vertices and 613 edges at 0x7f25204da438>, at 0x7f24d806d588>
_ = state.draw(pos=g.vp.pos, output="./.graph_theory/figures/football-sbm-fit.png")

Figure 7: Graph of the football-dataset with the different communities colored.
%matplotlib inline import matplotlib.pyplot as plt edges = state.get_matrix() _ plt.matshow(edges.todense())
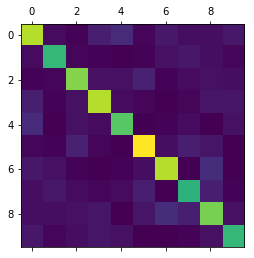
Figure 8: Connections between the different clusters (and the degrees within the clusters along the diagonal)
Course
Notation
Graph is a pair
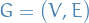 where
where 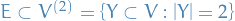 , e.g.
, e.g.

- Order of
 refers to
refers to  , which is often denoted
, which is often denoted 
- Size of
 is |E(G)|$, often denoted
is |E(G)|$, often denoted 
- Will only deal with simple graphs (or rather, the def above only includes simple graphs)
 often used to refer to the edge
often used to refer to the edge 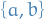
- If
 we say "
we say " is adjacent to
is adjacent to  " and might write
" and might write 
Two graphs
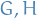 are *isomorphic$ if there exists a bijection
are *isomorphic$ if there exists a bijection  such that
such that

i.e. edge-preserving bijection between vertices
 is empty graph of order
is empty graph of order  and size 0
and size 0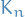 is complete graph of order
is complete graph of order  and size
and size 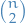 , i.e. all pairs vertices adjacent
, i.e. all pairs vertices adjacent is a path of order
is a path of order  and size
and size 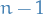
 is a circuit of order
is a circuit of order  and size
and size  , i.e. just a path with the ends joined, or a cycle
, i.e. just a path with the ends joined, or a cycle- A subgraph of
 is a graph
is a graph  with
with  and
and  (so every graph of order
(so every graph of order  is a subgraph of
is a subgraph of 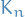 )
) - A subgraph of
 induced by the subset
induced by the subset 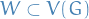 written
written ![$G[W]$](../../assets/latex/graph_theory_f3bb08e5180801458aa10dfc6cf46a9e088d1b95.png) is the graph
is the graph  , i.e. the vector set
, i.e. the vector set 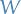 and all edges of
and all edges of  lying inside
lying inside 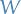
Lecture 1
The components of  are the maximal connected subgraphs induced by the equivalence classes of the relation "there is a u-v-path or
are the maximal connected subgraphs induced by the equivalence classes of the relation "there is a u-v-path or  ".
".
A forest is a graph containing no circuit.
A tree is a connected forest, i.e. components of a forest are trees. Equivalently, it's connected but has no circuit.
The following are equivalent
 is a tree (connected but has no circuit)
is a tree (connected but has no circuit) is minimal connected, i.e.
is minimal connected, i.e.  is connected but removal of any edge kills connectivity
is connected but removal of any edge kills connectivity is maximial circuit-free, i.e.
is maximial circuit-free, i.e.  has no circuit, but addition of any new edge creates a circuit
has no circuit, but addition of any new edge creates a circuit
 : Let
: Let  be connected circuit free. Suppose
be connected circuit free. Suppose  and
and 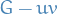 is connected (i.e.
is connected (i.e.  without the edge
without the edge  ). Then there is a path
). Then there is a path  in
in 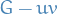 , so
, so  contains the circuit
contains the circuit  . Thus contradiction means
. Thus contradiction means  is minimal connected.
is minimal connected.
 : Let
: Let  be minimal conected. Suppose
be minimal conected. Suppose  has a circuit
has a circuit  and let
and let  . Then,
. Then,  and
and 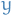 are connected by at least two paths, so we can remove one edge along one of these paths but
are connected by at least two paths, so we can remove one edge along one of these paths but  still remain connected
still remain connected 
 is circuit-free.
is circuit-free.
 : Let
: Let  be a tree. If
be a tree. If  there is a path
there is a path  in
in  from
from  to
to  , so
, so  is a circuit in
is a circuit in  . So
. So  is maximal circuit-free.
is maximal circuit-free.
 : Let
: Let  be maximal circuit-free. Let
be maximal circuit-free. Let  . Either
. Either  or
or  has a circuit
has a circuit  so
so 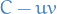 is a u-v-path in
is a u-v-path in  . Either way
. Either way  is joined to
is joined to  , so
, so  is connected.
is connected.
Discrete Exterior Calculus
- Great quick overview of the idea: http://www.cs.jhu.edu/~misha/Fall09/17-dec.pdf
- Based on a set of notes which looks really promising: desbrun05_discr_exter_calcul