Theory
Table of Contents
Overview
This document covers a lot of the more "pure" sides of Machine Learning, e.g. attempts at establishing bounds on convergence.
Most of this is built upon the Probably Approximately Correct (PAC) framework, which attempts to bound the errors the generalization of models.
Good sources, where I've gotten a lot of this from:
Notation
![$[m] = \left\{ 1, \dots, m \right\}$](../../assets/latex/theory_e48738a920711d373ed16fd09958ff87095e9692.png) , for a
, for a 
 denotes the result of applying
denotes the result of applying 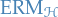 to
to  ,
,

 denotes the true risk of
denotes the true risk of  , where
, where 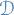 is the distribution, and
is the distribution, and  the labelling-function
the labelling-function denotes denotes the probability of getting a nonrepresentative sample, and we say
denotes denotes the probability of getting a nonrepresentative sample, and we say  is the confidence parameter of our prediction
is the confidence parameter of our prediction denotes the accuracy parameter, dealing with the fact that we cannot guarantee perfect label prediction:
denotes the accuracy parameter, dealing with the fact that we cannot guarantee perfect label prediction:  is a failure of the learner, while
is a failure of the learner, while  means we view the output of the learner as approximately correct
means we view the output of the learner as approximately correct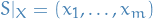 denotes an instance of the training set
denotes an instance of the training setEmpirical Risk Minimization rule is denoted:

i.e. the set of learners which minimizes the empirical risk
 .
.
bb* Empirical Risk Minimization (EMR) Standard Empirical Risk Minimization: minimize the empirical loss
![\begin{equation*}
L_S(h) = \frac{\big| i \in [m] : h(x_i) \ne y_i \big|}{m}
\end{equation*}](../../assets/latex/theory_74e054325d90d9d067186062e0163ec406f7dcd4.png)
A risk function is the expected loss of classifier  wrt. the probability distribution
wrt. the probability distribution 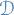 over
over  , namely
, namely
![\begin{equation*}
L_{\mathcal{D}}(h) := \mathbb{E}_{z \sim \mathcal{D}} \big[ \ell(h, z) \big]
\end{equation*}](../../assets/latex/theory_29844aa82ccf60f88e7bd1990968e7e911ffb140.png)
Empirical risk is the expected loss over a given sample  , namely,
, namely,
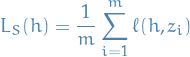
Finite Hypothesis Classes
- Simple restriction in attempt to avoid "overfitting" is to bound the size of the hypotheses; i.e. consider a restricted hypothesis class

For now we make the following assumption:
There exists  such that
such that

That is, there exists an optimal hypothesis in the restricted hypothesis class  which obtaines the global minimum true risk, i.e. minimum loss over the full data distribution.
which obtaines the global minimum true risk, i.e. minimum loss over the full data distribution.
Hence, we would like to upper bound the probability to sample m-tuple of instances which lead to failure. That is, find an upper bound for
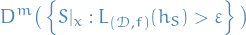
Then let
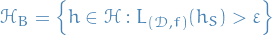
i.e. all the "bad" hypotheses, such that the probability of failure of the learner is greater than  .
.
Further, let
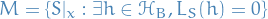
i.e. 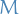 is set of all training instances which would "mislead" us into believing one of the wrong hypotheses (
is set of all training instances which would "mislead" us into believing one of the wrong hypotheses ( ) is "good" (i.e. has zero average loss on the training data).
) is "good" (i.e. has zero average loss on the training data).
With our Realizability Assumption (i.e. that 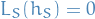 ), then
), then
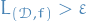
can only happen if for some  we have
we have  . That is,
. That is,

which means that

Further, we can rewrite
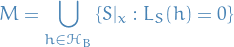
Hence,
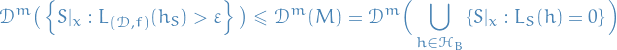
To summarize: probability of learner failing in an  sense, is bounded above by the probability of the learner being a misleading learner, i.e. having minimal training error and being in the "bad" hypotheses class.
sense, is bounded above by the probability of the learner being a misleading learner, i.e. having minimal training error and being in the "bad" hypotheses class.
And because of how probability-measures work, probabilities of finite unions can be written
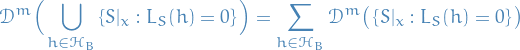
Suppose now that  . By definition,
. By definition,
![\begin{equation*}
L_S(h) = 0 \iff h(x_i) = f(x_i), \quad \forall i \in [m]
\end{equation*}](../../assets/latex/theory_b3758f6f4d9f1cad2d3084269620aeea0b207656.png)
and due to the i.i.d. sampling of the training set, the joint probability of this occuring is then
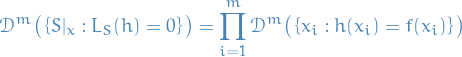
Further, for each individual sample in the training set we have

where the last inequality follows from the fact that  .
.

simply denotes the probability of this  correctly labelling the
correctly labelling the  over the entire true distribution
over the entire true distribution  . Since these equalities are indicator variables, thus binary, this corresponds to the expectation
. Since these equalities are indicator variables, thus binary, this corresponds to the expectation
![\begin{equation*}
\mathbb{E} \big[ h(x) = y \big]
\end{equation*}](../../assets/latex/theory_aad9a2c6302bdd5b3ce6249f854b3daefd6c396a.png)
and since ![$L_{(\mathcal{D}, f)}(h) = \mathbb{E}[h(x) \ne y]$](../../assets/latex/theory_0036225e85859650509a9ed460eb7d4ae280a843.png) by definition, we have
by definition, we have

which is the second equality in the above expression.
Finally, observing that for  , we have
, we have

we obtain
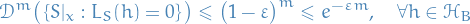
Combining this with the sum over the  we saw earlier, we conclude that
we saw earlier, we conclude that

Let
 be a finite hypothesis class
be a finite hypothesis class

 such that
such that
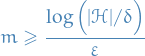
Then, for any labeling function  , and any distribution
, and any distribution 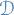 , for which the realizability assumption holds, over the choice of an i.i.d. sample
, for which the realizability assumption holds, over the choice of an i.i.d. sample  of size
of size  , we have that for every ERM hypothesis,
, we have that for every ERM hypothesis,  ,
,

That is, the 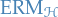 rule over a finite hypothesis class will be probably (with confidence
rule over a finite hypothesis class will be probably (with confidence  ) approximately (up to error
) approximately (up to error  ) correct (PAC).
) correct (PAC).
Probably Approximately Correct (PAC)
A hypothesis class  is PAC learnable if there exist a function
is PAC learnable if there exist a function 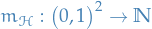 and a learning algorithm with the property:
and a learning algorithm with the property:
- for every

- for every distribution
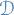 over
over 
- for every labeling function

if the realizable assumption holds wrt.  ,
, 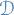 , and
, and  , then when running the learning algorithm on
, then when running the learning algorithm on  i.i.d. examples generated by
i.i.d. examples generated by 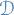 and labeled by
and labeled by  , the algorithm returns a hypothesis
, the algorithm returns a hypothesis  s.t.
s.t.

We will often refer to  as the sample complexity of learning
as the sample complexity of learning  .
.
 defines how far the output classifier can be from the optimal one
defines how far the output classifier can be from the optimal one is how likely the classifier is to meet the accuracy requirement
is how likely the classifier is to meet the accuracy requirement
Every finite hypothesis class is PAC learnable with sample complexity
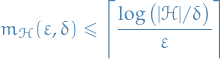
Agnostic PAC learning - relaxing realization assumption
A hypothesis class  is agnostic PAC learnable wrt a set
is agnostic PAC learnable wrt a set  and a loss function
and a loss function 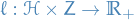 , if there exists a function
, if there exists a function 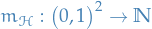 and an algorithm with the property
and an algorithm with the property
- for every

- for every distribution
 over
over 
when running the learning algorithm on  i.i.d. examples drawn from
i.i.d. examples drawn from 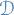 , the algorithm returns
, the algorithm returns  such that
such that
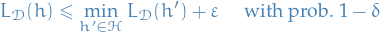
where
![\begin{equation*}
L_{\mathcal{D}}(h) = \underset{z \sim \mathcal{D}}{\mathbb{E}} \big[ \ell(h, z) \big]
\end{equation*}](../../assets/latex/theory_c4c6df9e2a99745e926ee1c19a74fe9174625abb.png)
Uniform convergence
A training sample  is called
is called  wrt. domain
wrt. domain  , hypothesis class
, hypothesis class  , loss function
, loss function  , and distribution
, and distribution 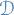 , if
, if

Assume that a training set is  .
.
Then, any output of  , namely, any
, namely, any

satisfies

From Lemma 4.2 we know that a  rule
rule  is an agnostic PAC-learner if
is an agnostic PAC-learner if  is
is  with probability
with probability  !
!
This is motivates the following definition of Uniform Convergence:
We say that a hypothesis class  has the uniform convergence property (wrt. domain
has the uniform convergence property (wrt. domain  and loss
and loss  ) if there exists a function
) if there exists a function 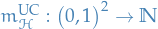 such that for
such that for
- every

- every probability distribution
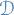 over
over 
if  is a sample of
is a sample of  examples drawn i.i.d. according to
examples drawn i.i.d. according to 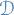 , then
, then  is
is  , with at least probability
, with at least probability  .
.
Let  be a sequence of i.i.d. random variables and assume that for all i,
be a sequence of i.i.d. random variables and assume that for all i,
![\begin{equation*}
\mathbb{E}[\theta_i] = \mu, \quad \mathbb{P} \big[ a \le \theta_i \le b \big] = 1
\end{equation*}](../../assets/latex/theory_8cb0ab9601c74549e2157fdd6800c0b65e0164b9.png)
Then, for any  ,
,
![\begin{equation*}
\mathbb{P} \Bigg[ \frac{1}{m} \left| \sum_{i=1}^{m} \theta_i - \mu \right| > \varepsilon \Bigg] \le 2 \exp \Big( - 2 m \varepsilon^2 / (b - a)^2 \Big)
\end{equation*}](../../assets/latex/theory_13cdda5683d593ca656e7a65bed422892021a6ae.png)
Using Hoeffding's Inequality, one can prove the following:
Let  be a finite hypothesis class, let
be a finite hypothesis class, let  be a domain, and let
be a domain, and let ![$\ell: \mathcal{H} \times Z \to [0, 1]$](../../assets/latex/theory_bc182736c1681a336f1d30dfefbee990980ad370.png) be a loss function.
be a loss function.
Then,  enjoys the uniform convergence property with sample complexity
enjoys the uniform convergence property with sample complexity
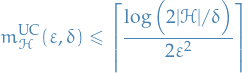
Furthermore, the class is agnostically PAC learnable using the ERM algorithm with sample complexity
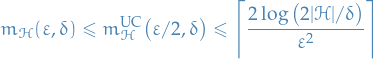
Even though Corollary 4.6 only holds for finite hypothesis in practice it might also provide us with upper bounds to "infinite" hypothesis classes, due to parameters most often being represented using floating point representations, which consists of 64 bits.
That is, if we're computationally approximating some  , there is only
, there is only 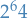 different values
different values  actually can take on. If we then have
actually can take on. If we then have  parameters, we can use Corollary 4.6 to obtain the following bound:
parameters, we can use Corollary 4.6 to obtain the following bound:
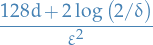
This is often referred to as the discretization trick.
Bias-Complexity Tradeoff
Let 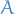 be any learning algorithm for the task of binary classification wrt. to the 0-1 loss over a domain
be any learning algorithm for the task of binary classification wrt. to the 0-1 loss over a domain  .
Let
.
Let  be any number smaller than
be any number smaller than 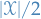 , representing a training set size.
, representing a training set size.
Then, there exists a distribution 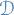 over
over 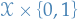 such that:
such that:
- There exists a function
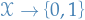 with
with 
With probability of at least
 over the choice of
over the choice of  we have that
we have that
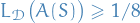
No-Free-Lunch theorem states that for every learner, there exists a task on which it fails even though that task can be successfully learned by another learner.
Let  such that
such that 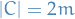 .
.
We will prove this using the following intuition:
- Any learning algorithm that observes only half of the instances in
 has no information on what should be the labels of the rest of the instances in
has no information on what should be the labels of the rest of the instances in 
- Therefore, there exists a "reality", that is some target function
 , that would contradict the labels that
, that would contradict the labels that 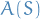 predicts on the unobserved instances in
predicts on the unobserved instances in 
Since 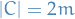 by assumption, there are
by assumption, there are  unique mappings
unique mappings  . Denote these
. Denote these  . For each
. For each  , let
, let 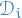 be a distribution over
be a distribution over 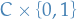 defined by
defined by
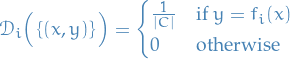
Then we have

We can combine Lemma lemma:no-free-lunch-theorem-intermediate-lemma-1 with Lemma lemma:shalev2014understanding-B1, from which we observe
![\begin{equation*}
\mathbb{P} \big[ Z > 1 / 8 \big] \ge \frac{\mu - 1 / 8}{1 - 1 / 8} = \frac{\mu - 1 / 8}{7 / 8} = \frac{8}{7} \mu - \frac{1}{7} \ge \frac{8}{7} \cdot \frac{1}{4} - \frac{1}{7} = \frac{2}{7} - \frac{1}{7} = \frac{1}{7}
\end{equation*}](../../assets/latex/theory_99828d111f908678e499221c45fb63f2f9d1915f.png)
where we've used ![$\mu = \mathbb{E} \big[ L_{\mathcal{D}} \big( A(S) \big) \big] \ge \frac{1}{4}$](../../assets/latex/theory_0f884bc814a935b8e8c0d7cd66938e9007c24c74.png) . Hence,
. Hence,
![\begin{equation*}
\mathbb{P} \big[ Z > 1 / 8 \big] \ge \frac{1}{7}
\end{equation*}](../../assets/latex/theory_19525aa0d12d16d7f02eed077b99223ceac0d2e4.png)
concluding our proof.
For every algorithm 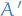 , that receives a training set of
, that receives a training set of  examples from
examples from 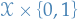 there exists a function
there exists a function  and a distribution
and a distribution 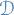 over
over 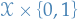 , such that
, such that  and
and
![\begin{equation*}
\underset{S \sim D^m}{\mathbb{E}} \big[ L_{\mathcal{D}} \big( A(S) \big) \big] \ge \frac{1}{4}
\end{equation*}](../../assets/latex/theory_a1c4e7f382321f7d66dcaf658da5870106a494a2.png)
Let 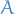 be some algorithm that receives a training set of
be some algorithm that receives a training set of  examples from
examples from 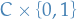 and returns a function
and returns a function 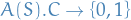 , i.e.
, i.e.
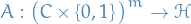
There are  possible sequences of
possible sequences of  samples from
samples from  . Let
. Let
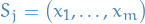
and

i.e.  denotes the sequences containing instances in
denotes the sequences containing instances in  labeled by
labeled by  .
.
If the distribution is 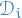 , as defined above, then the possible training sets
, as defined above, then the possible training sets 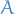 can receive are
can receive are  , and all these training sets have the same probability of being sampled. Therefore,
, and all these training sets have the same probability of being sampled. Therefore,
![\begin{equation*}
\underset{S \sim \mathcal{D}_i^m}{\mathbb{E}} \big[ L_{\mathcal{D}_i} \big( A(S) \big) \big] = \frac{1}{k} \sum_{j=1}^{k} L_{\mathcal{D}_i} \big( A(S_j^i) \big)
\end{equation*}](../../assets/latex/theory_54c15d0e007a14b378c209842fc6c637edc0fc95.png)
Using the fact that maximum is larger than average, and average is larger than minimum, we have
![\begin{equation*}
\begin{split}
\max_{i \in [T]} \frac{1}{k} \sum_{j=1}^{k} L_{\mathcal{D}_i} \big( A(S_j^i) \big)
& \ge \frac{1}{T} \sum_{i=1}^{T} \frac{1}{k} \sum_{j=1}^{k} L_{\mathcal{D}_i} \big( A(S_j^i) \big) \\
&= \frac{1}{k} \sum_{j=1}^{k} \frac{1}{T} \sum_{i=1}^{T} L_{\mathcal{D}_i} \big( A(S_j^i) \big) \\
& \ge \min_{j \in [k]} \frac{1}{T} \sum_{i=1}^{T} L_{\mathcal{D}_i} \big( A(S_j^i) \big)
\end{split}
\end{equation*}](../../assets/latex/theory_9c33a8e69751300944324af64bf4bb90a2cbd088.png)
The above equation is saying that the maximum risk expected over possible rearrangements of  achieved by
achieved by  is greater than the minimum of the expected risk over possible
is greater than the minimum of the expected risk over possible  using the optimal arrangement ordering of
using the optimal arrangement ordering of  .
.
Now, fix some ![$j \in [k]$](../../assets/latex/theory_e747e9c4bf21f864dade19712be4f9737aba2dfc.png) , and denote
, and denote 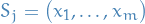 and let
and let  be the examples in
be the examples in  that do not appear in
that do not appear in  , i.e.
, i.e.
![\begin{equation*}
v_a : v_a \ne x_b, \quad \forall b \in [m], \quad \forall a \in [p]
\end{equation*}](../../assets/latex/theory_503415d205068bcf09fab029494e338c8ebb50ad.png)
Clearly  , since we're assuming
, since we're assuming 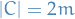 and
and  , and therefore the "best" case scenario is if we get
, and therefore the "best" case scenario is if we get  distinct samples.
distinct samples.
Therefore, for every function  and every
and every ![$i \in [T]$](../../assets/latex/theory_2b7ffbfdd966e63b901eb26d45b24c63addbb938.png) we have
we have
![\begin{equation*}
\begin{split}
L_{\mathcal{D}_i}(h) &= \frac{1}{2m} \sum_{x \in C}^{} \mathbbm{1} \big[ h(x) \ne f_i(x) \big] \\
&\ge \frac{1}{2m} \sum_{r=1}^{p} \mathbbm{1} \big[ h(v_r) \ne f_i(v_r) \big] \\
&\ge \frac{1}{2p} \sum_{r=1}^{p} \mathbbm{1} \big[ h(v_r) \ne f_i(v_r) \big]
\end{split}
\end{equation*}](../../assets/latex/theory_89d4504df8478e45b5ad0f75553930d365522496.png)
Hence,
![\begin{equation*}
\begin{split}
\frac{1}{T} \sum_{i=1}^{T} L_{\mathcal{D}_i} \Big( A(S_j^i) \Big)
& \ge \frac{1}{T} \sum_{i=1}^{T} \frac{1}{2p} \sum_{r=1}^{p} \mathbbm{1} \big[ A(S_j^i)(v_r) \ne f_i(v_r) \big] \\
& = \frac{1}{2p} \sum_{r=1}^{p} \frac{1}{T} \sum_{i=1}^{T} \mathbbm{1} \big[ A(S_j^i)(v_r) \ne f_i(v_r) \big] \\
&\ge \frac{1}{2} \min_{r \in [p]} \frac{1}{T} \sum_{i=1}^{T} \mathbbm{1} \big[ A(S_j^i)(v_r) \ne f_i(v_r) \big]
\end{split}
\end{equation*}](../../assets/latex/theory_837c0656c73067f8c03f39b4131a8517d0623cb0.png)
Next, fix some ![$r \in [p]$](../../assets/latex/theory_af9cabe0b509536fa1e8dd275c59c10895690fd9.png) .
.
We can partition all the functions in  into
into  disjoint pairs, where for a pair
disjoint pairs, where for a pair  we have
we have

Since such a pair must have  , it follows that
, it follows that
![\begin{equation*}
\mathbbm{1} \big[ A(S_j^i)(v_r) \ne f_i(v_r) \big] + \mathbbm{1} \big[ A(S_j^{i'})(v_r) \ne f_i(v_r) \big] = 1
\end{equation*}](../../assets/latex/theory_db3b3acb6a83d70a8cb70922d42a1f9e75e8e7e3.png)
which yields
![\begin{equation*}
\frac{1}{T} \sum_{i=1}^{T} \mathbbm{1} \big[ A(S_j^i)(v_r) \ne f_i(v_r) \big] = \frac{1}{2}
\end{equation*}](../../assets/latex/theory_26129d3eaaff46597e6d6f2219ed18ff8cdff17b.png)
Substituting this back into
![\begin{equation*}
\frac{1}{T} \sum_{i=1}^{T} L_{\mathcal{D}_i} \Big( A(S_j^i) \Big) \ge \frac{1}{2} \min_{r \in [p]} \frac{1}{T} \sum_{i=1}^{T} \mathbbm{1} \big[ A(S_j^i)(v_r) \ne f_i(v_r) \big] = \frac{1}{4}
\end{equation*}](../../assets/latex/theory_9cc600295632d0c840acd933a3c30bfd4192d79a.png)
and this into
![\begin{equation*}
\max_{i \in [T]} \underset{S \sim \mathcal{D}_i^m}{\mathbb{E}} \big[ L_{\mathcal{D}_i} \big( A(S_j^i) \big) \big] \ge \max_{i \in [T]} \frac{1}{k} \sum_{j=1}^{k} L_{\mathcal{D}_i} \big( A(S_j^i) \big) \ge \frac{1}{T} \sum_{i=1}^{T} L_{\mathcal{D}_i} \big( A(S_j^i) \big) \ge \frac{1}{4}
\end{equation*}](../../assets/latex/theory_ac6452828388149bad7ea23298433af7ed9253a3.png)
Hence, there exists a sample such that
![\begin{equation*}
\underset{S \sim \mathcal{D}^m}{\mathbb{E}} \Big[ L_{\mathcal{D}} \big( A'(S) \big) \Big] \ge \frac{1}{4}
\end{equation*}](../../assets/latex/theory_aa71d53738c4bca50b58a3bbc6b9635aa73fd476.png)
for every algorithm 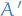 .
.
We decompose the error of an 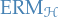 predictor into two components as follows.
predictor into two components as follows.
Let  be an
be an 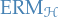 hypothesis. Then, we can write
hypothesis. Then, we can write

where
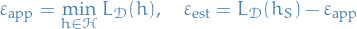
 denotes the approximation error, which is the minimum possible risk achievable by a predictor in the given hypothesis class
denotes the approximation error, which is the minimum possible risk achievable by a predictor in the given hypothesis class 
 denotes the estimation error, which is the difference between the best achivable error and the error achieved by
denotes the estimation error, which is the difference between the best achivable error and the error achieved by 
The VC-Dimension
Let  be a class of functions from
be a class of functions from  to
to  , and let
, and let  .
.
The restriction of  to
to  is the set of functions
is the set of functions  which can be derived from
which can be derived from  . That is,
. That is,

A hypothesis class  shatters a finite set
shatters a finite set  if the restriction of
if the restriction of  to
to  is the set of all functions
is the set of all functions  .
.
That is, if  .
.
Shattering is basically a way of stating
- All functions mapping from the subset
 to the set of binary labels
to the set of binary labels - If the hypothesis-class we're trying to learn contains all possible functions from
 to
to 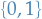 then we say it's shattered, and this indicates that it will be difficult (if not impossible) to learn due to the fact that if
then we say it's shattered, and this indicates that it will be difficult (if not impossible) to learn due to the fact that if  and
and  is shattered by
is shattered by  , i.e.
, i.e.  is the set of all possible mappings
is the set of all possible mappings 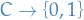 , then
, then  is not PAC-learnable, since we cannot satisfy arbitrary bounds simply by adjusting the number of samples.
is not PAC-learnable, since we cannot satisfy arbitrary bounds simply by adjusting the number of samples.
The VC-dimension of a hypothesis class  denoted
denoted  , is the maximal size of a set
, is the maximal size of a set  that can be shattered by
that can be shattered by  .
.
If  can shatter sets of arbitrarily large size, we say that
can shatter sets of arbitrarily large size, we say that  has infinite VC-dimension.
has infinite VC-dimension.
Let  be a class of infinite VC-dimension. Then,
be a class of infinite VC-dimension. Then,  is not PAC-learnable.
is not PAC-learnable.
Generalization
Here we will consider generalization on classification tasks using PAC-learning theory.
Notation
 samples of inputs and outputs
samples of inputs and outputs distribution on labelled data
distribution on labelled data denotes
denotes  i.i.d. samples of data bpoints
i.i.d. samples of data bpoints 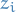 from
from  (often just write
(often just write  , and have the
, and have the  be implied)
be implied) denotes the set of classifiers / hypotheses
denotes the set of classifiers / hypotheses  which we consider to explain the data
which we consider to explain the data denotes the loss of classifier
denotes the loss of classifier  on point
on point 
 denotes the average loss of classifier
denotes the average loss of classifier  on the sample-set
on the sample-set  , i.e.
, i.e.
![\begin{equation*}
L_{S_m}(h) = \mathbb{E}_{z \sim S_m} \big[ l(h, z) \big]
\end{equation*}](../../assets/latex/theory_d864767f037ebaa9e2bee726499f0435dd228e35.png)
 denotes the average loss over the entire distribution
denotes the average loss over the entire distribution  :
:
![\begin{equation*}
L_D(h) = \mathbb{E}_{z \sim D} \big[ l(h, z) \big]
\end{equation*}](../../assets/latex/theory_2d2eaec18723189c27918935071b169b0d483c36.png)
Generalization error

Generalization under ERM
The objective is

i.e.  which best explains the dataset, which is Empirical Risk Minimization since we're minimizing the empirical loss.
which best explains the dataset, which is Empirical Risk Minimization since we're minimizing the empirical loss.
We then define the generalization error as follows:
The generalization error is defined

which measures how well hypothesis  generalizes to a distribution
generalizes to a distribution  when its performance on a sample
when its performance on a sample  drawn from
drawn from  is known.
is known.
Generalization Theory
- Generalization theory attempts to upper bound the
 from the generalization error
from the generalization error
Rademacher Complexity
- Formalize notion of complexity of a hypothesis

Let
 is the hypothesis class
is the hypothesis class is
is  i.i.d. samples from
i.i.d. samples from 
And then the coefficients
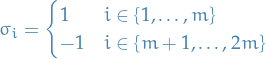
Then the Rademacher Complexity of  on a distribution
on a distribution  is defined as
is defined as
![\begin{equation*}
\mathcal{R}_{m, D}(\mathcal{H}}) = \underset{S \sim D^m}{\mathbb{E}} \Bigg[ \frac{1}{2m} \sup_{h \in \mathcal{H}} \Big| \sum_{i=1}^{2m} \sigma_i h(z_i) \Big| \Bigg]
\end{equation*}](../../assets/latex/theory_24f2a36b15f5a91fd190668d0d239988b2208b41.png)
The 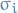 simply flip the sign of the classification (we're assuming
simply flip the sign of the classification (we're assuming  for all
for all  ) simply changes the classification of
) simply changes the classification of  to opposite one.
to opposite one.
This therefore corresponds to flipping the labels of half the datapoints randomly and retaining the labels of the other half. We choose the  which correlates well with this random relabeling (if half classified as positive and half classified as negative, and then for this specific
which correlates well with this random relabeling (if half classified as positive and half classified as negative, and then for this specific  we just happen to flip all the the ones which are positive to negative, then we get our
we just happen to flip all the the ones which are positive to negative, then we get our  ).
).
I struggle a bit with interpreting the Rademacher Complexity intuitively. Why would this indicate high complexity of the hypothesis class?
- Because we can consider ….
For a given loss function  , we have that the generalization error of all hypothesis
, we have that the generalization error of all hypothesis  on a sample
on a sample  of
of  i.i.d. samples drawn from a distribution
i.i.d. samples drawn from a distribution  , is
, is
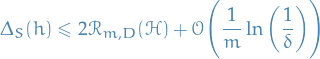
for all  , with probability
, with probability  .
.
Hence, the generalization error  of a hypothesis
of a hypothesis  can be upper bounded by the Rademacher complexity.
can be upper bounded by the Rademacher complexity.
This is more a sketch of the poof.
Suppose for a random sample  the generalization error is high. Then
the generalization error is high. Then
- Split
 into sets
into sets 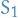 and
and 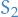 randomly, with sets being of equal size
randomly, with sets being of equal size - For a given
 (picked independently of
(picked independently of  ), consider
), consider 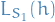 and
and 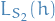
For large
 , we have
, we have  and thus
and thus

(with
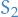 being sort of like our "test" set and
being sort of like our "test" set and 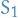 the "training" set). Thus
the "training" set). Thus
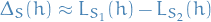
Since
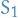 and
and 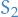 are picked randomly, we can just consider
are picked randomly, we can just consider 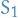 as the first half of the samples
as the first half of the samples  and then the difference reduces to
and then the difference reduces to
![\begin{equation*}
\begin{split}
\underset{S \sim D^m}{\mathbb{E}} \Bigg[ \underset{z \sim S_2}{\mathbb{E}} \big[ L(h, z) \big] - \underset{z \sim S_1}{\mathbb{E}} \big[ L(h, z) \big] \Bigg]
&\le \underset{S \sim D^m}{\mathbb{E}} \Bigg[ \frac{1}{m} \Big| \sum_{i=1}^{m} \sigma_i h_i(z_i) \Big| \Bigg] \\
& \le \sup_{h \in \mathcal{H}} \underset{S \sim D^m}{\mathbb{E}} \Bigg[ \frac{1}{m} \Big| \sum_{i=1}^{m} \sigma_i h(z_i) \Big| \Bigg]
\end{split}
\end{equation*}](../../assets/latex/theory_fe018defdb8934ceaa73642e1611b9cdf66258dc.png)
Thus we have
![\begin{equation*}
\begin{split}
\Delta_S(h) & \le \sup_{h \in \mathcal{H}} \underset{S \sim D^m}{\mathbb{E}} \Bigg[ \Big| \frac{1}{m} \sum_{i=1}^{m} \sigma_i h(z_i) \Big| \Bigg] \\
& \le \underset{S \sim D^m}{ \mathbb{E}} \Bigg[ \sup_{h \in \mathcal{H}} \frac{1}{m} \Big| \sum_{i=1}^{m} \sigma_i h(z_i) \Big| \Bigg] = 2 \mathcal{R}_{m, D}(\mathcal{H})
\end{split}
\end{equation*}](../../assets/latex/theory_e7a7026f7b7bc9ee56f24bdd3e81e49f2aca981a.png)
where the factor of
 is simply due to our definition of Rademacher complexity involving
is simply due to our definition of Rademacher complexity involving  .
We also leave out the "concentration term" (I believe this depends on the "variance" of the underlying distribution)
.
We also leave out the "concentration term" (I believe this depends on the "variance" of the underlying distribution)
Let
 be a sequence of independent random variables taking on values in a set
be a sequence of independent random variables taking on values in a set 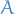
 be a sequence of positive real constants
be a sequence of positive real constants
If  satisfies
satisfies

for  , then
, then
![\begin{equation*}
\mathbb{P} \big( \left\{ \varphi(z_1, \dots, z_m) - \mathbb{E}_{z_1, \dots, z_m} \big[ \varphi(z_1, \dots, z_m) \big] \right\} \ge \varepsilon \big) \le \exp \bigg( - \frac{2 \varepsilon^2}{\sum_{i=1}^{n} c_i^2} \bigg)
\end{equation*}](../../assets/latex/theory_e07a5b5139b94c8570bac7e484c5d01aec88de38.png)
Let
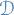 be a fixed distribution over the space
be a fixed distribution over the space 
 be a given constant
be a given constant be a set of bounded functions, wlog. we in particular assume
be a set of bounded functions, wlog. we in particular assume ![$\mathcal{F} \subseteq \left\{ f: Z \to [0, 1] \right\}$](../../assets/latex/theory_b9b00a1f655c36361ead9aae84eefee57fde4236.png)
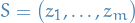 be a sequence of i.i.d. samples from
be a sequence of i.i.d. samples from 
Then, with probability at least  over the draw of
over the draw of  , for every function
, for every function  ,
,
![\begin{equation*}
\mathbb{E}_D \big[ f(z) \big] \le \widehat{\mathbb{E}}_S \big[ f(z) \big] + 2 R_m(\mathcal{F}) + \sqrt{\frac{\log (1 / \delta)}{m}}
\end{equation*}](../../assets/latex/theory_a655ec27a00c1747ff46e12ccc36c29cf89898be.png)
We have
![\begin{equation*}
\mathbb{E}_D \big[ f(z) \big] - \widehat{\mathbb{E}}_S \big[ f(z) \big] \le \sup_{h \in \mathcal{F}} \bigg( \mathbb{E}_D \big[ h(z) \big] - \widehat{\mathbb{E}}_S \big[ h(z) \big] \bigg)
\end{equation*}](../../assets/latex/theory_84daf4a8bc90fb07b1c4aab73fda6289e8cc3ac2.png)
so
![\begin{equation*}
\mathbb{E}_D \big[ f(z) \big] \le \widehat{\mathbb{E}}_S \big[ f(z) \big] + \sup_{h \in \mathcal{F}} \bigg( \mathbb{E}_D \big[ h(z) \big] - \widehat{\mathbb{E}}_S \big[ h(z) \big] \bigg)
\end{equation*}](../../assets/latex/theory_db38593444cbdefaf28694012b4389db933392c3.png)
Consider letting
![\begin{equation*}
\varphi(S) = \sup_{h \in \mathcal{F}} \mathbb{E}_D \big[ h(z) \big] - \widehat{\mathbb{E}}_S \big[ h(z) \big]
\end{equation*}](../../assets/latex/theory_341e02b0cc9855b2d7325d310943944d11d475cd.png)
Let 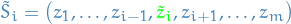 with
with 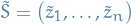 being identitically distributed as
being identitically distributed as  . Then
. Then
![\begin{equation*}
\left| \varphi \big( S \big) - \varphi \big( \tilde{S}_i \big) \right| = \left| \widehat{\mathbb{E}}_{S} \big[ h(z) \big] - \widehat{\mathbb{E}}_{\tilde{S}_i} \big[ h(z) \big] \right| = \frac{1}{m} \sup_{h \in \mathcal{F}} \left| h(z_i) - h(\tilde{z}_i) \right|
\end{equation*}](../../assets/latex/theory_6c7ad988ae7e5f3ff1468f787ba05d33a0e5fed3.png)
and, finally, since 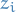 are bounded and we assume
are bounded and we assume  are all bounded, we can wlog. assume
are all bounded, we can wlog. assume

Thus,
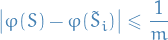
Using McDarmid's inequality, this implies that
![\begin{equation*}
\mathbb{P} \big( \varphi(S) - \mathbb{E}_S \big[ \varphi(S) \big] \ge t \big) \le e^{- t^2 / \big( \frac{1}{m} \sum_{i=1}^{m} \frac{1}{m^2} \big)} = e^{- t^2 m}
\end{equation*}](../../assets/latex/theory_72bda96b07f0b30a1f7a70cbe508f2120f1dce22.png)
One issue: don't yet know how to compute ![$\mathbb{E} [ \varphi(S) ]$](../../assets/latex/theory_c7d1727fd9c48b56934ea441bfd80065ecdc0331.png) !
!
First let's solve for  such that the above probability is
such that the above probability is  :
:
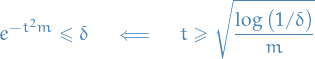
And since
![\begin{equation*}
\mathbb{P} \Big( \left\{ \varphi(S) - \mathbb{E}_S[\varphi(S)] \le t \right\} \Big) = 1 - \mathbb{P} \Big( \left\{ \varphi(S) - \mathbb{E}_S \big[ \varphi(S) \big] \ge t \right\} \Big) \ge 1 - \delta
\end{equation*}](../../assets/latex/theory_5771eb8287a2e11588256d14e1f3ab4dec25015d.png)
which is what we want. Thus, with probability at least  , we have deduced that
, we have deduced that
![\begin{equation*}
\varphi(S) \le \mathbb{E}_S \big[ \varphi(S) \big] + \underbrace{\sqrt{\frac{\log(1 / \delta)}{m}}}_{t}
\end{equation*}](../../assets/latex/theory_7840784d87c955584e08bd850bff99b1a059352d.png)
and thus, substituting into our original bound on ![$\mathbb{E}_D \big[ f(z) \big]$](../../assets/latex/theory_d0297aeb185fe32963d68707b0d06938fe94f7c3.png) ,
,
![\begin{equation*}
\begin{split}
\mathbb{E}_D \big[ f(z) \big] &= \widehat{\mathbb{E}}_S \big[ f(z) \big] + \sup_{h \in \mathcal{F}} \bigg( \mathbb{E}_D \big[ h(z) \big] - \widehat{\mathbb{E}}_S \big[ h(z) \big] \bigg) \\
&= \widehat{\mathbb{E}}_S \big[ f(z) \big] + \varphi(S) \\
&\le \widehat{\mathbb{E}}_S \big[ f(z) \big] + \mathbb{E}_S \big[ \varphi(S) \big] + \sqrt{\frac{\log(1 / \delta)}{m}} \\
&= \widehat{\mathbb{E}}_S \big[ f(z) \big] + \mathbb{E}_S \Bigg[ \sup_{h \in \mathcal{F}} \bigg( \mathbb{E}_D\big[h(z)\big] - \widehat{\mathbb{E}}_S \big[h(z)\big] \bigg) \Bigg] + \sqrt{\frac{\log(1 / \delta)}{m}}
\end{split}
\end{equation*}](../../assets/latex/theory_dffd2c12fed70a47159ec08c72b43fc7579c1d4f.png)
with probability at least  .
.
We're now going to make use of a classic symmetrization technique. Observe that due to the independence of the samples
![\begin{equation*}
\mathbb{E}_{\tilde{S}} \Big[ \widehat{\mathbb{E}}_{\tilde{S}} \big[ h(z) \big] \mid S \Big] = \frac{1}{m} \sum_{i=1}^{m} \underbrace{\mathbb{E}_{\tilde{S}} \big[ h(\tilde{z}_i) \mid S \big]}_{= \mathbb{E}_D [ h(z)]} = \frac{1}{m} \sum_{i=1}^{m} \mathbb{E}_D \big[h(z) \big] = \mathbb{E}_D \big[ h(z) \big]
\end{equation*}](../../assets/latex/theory_d333df714ae9c2d3617e96ed255c177bfa815ec6.png)
and
![\begin{equation*}
\mathbb{E}_{\tilde{S}} \Big[ \widehat{\mathbb{E}}_S \big[ h(z) \big] \mid S \Big] = \widehat{\mathbb{E}}_S \big[ h(z) \big]
\end{equation*}](../../assets/latex/theory_53fed5ac59704b268231cbe76202c62c355deef9.png)
The reason why we're writing ![$\mathbb{E}_{\tilde{S}} \big[ \hat{\mathbb{E}}_S[h(z)] \mid S \big]$](../../assets/latex/theory_2d83569a498549c417814749235c3f3ef1019ff2.png) rather than just
rather than just ![$\mathbb{E}_{\tilde{S}} \big[ \hat{\mathbb{E}}_S[h(z)] \big]$](../../assets/latex/theory_234dd6e14ed192c0eb666ca6d40d47ee138ff793.png) is because, if we're being rigorous, we're really taking the expectation over the 2m-dimensional product-space.
is because, if we're being rigorous, we're really taking the expectation over the 2m-dimensional product-space.
Therefore, we can write
![\begin{equation*}
\begin{split}
\mathbb{E}_S \Bigg[ \sup_{h \in \mathcal{F}} \bigg( \mathbb{E}_D \big[ h(z) \big] - \widehat{\mathbb{E}}_S \big[ h(z) \big] \bigg) \Bigg] &= \mathbb{E}_S \Bigg[ \sup_{h \in \mathcal{F}} \bigg( \mathbb{E}_{\tilde{S}} \Big[ \widehat{\mathbb{E}}_{\tilde{S}} \big[ h(z) \big] \mid S \Big] - \mathbb{E}_{\tilde{S}} \Big[ \widehat{\mathbb{E}}_S \big[ h(z) \big] \Big] \bigg) \Bigg] \\
&= \mathbb{E}_S \Bigg[ \sup_{h \in \mathcal{F}} \bigg( \mathbb{E}_{\tilde{S}} \Big[ \widehat{\mathbb{E}}_{\tilde{S}} \big[ h(z) \big] - \widehat{\mathbb{E}}_S \big[ h(z) \big] \mid S \Big] \bigg) \Bigg]
\end{split}
\end{equation*}](../../assets/latex/theory_718393a114422f73230338436d805530f5cb7d80.png)
Moreover, we can use the fact that  is a convex function, therefore Jensen's inequality tells us that
is a convex function, therefore Jensen's inequality tells us that
![\begin{equation*}
\begin{split}
\mathbb{E}_S \Bigg[ \sup_{h \in \mathcal{F}} \bigg( \mathbb{E}_{\tilde{S}} \Big[ \widehat{\mathbb{E}}_{\tilde{S}} \big[ h(z) \big] - \widehat{\mathbb{E}}_S \big[ h(z) \big] \mid S \Big] \bigg) \Bigg]
&\le \mathbb{E}_S \bigg[ \mathbb{E}_{\tilde{S}} \Big[ \sup_{h \in \mathcal{F}} \Big( \widehat{\mathbb{E}}_{\tilde{S}} \big[ h(z) \big] - \widehat{\mathbb{E}}_S \big[ h(z) \big] \Big) \mid S \Big] \bigg] \\
&= \mathbb{E}_{S, \tilde{S}} \bigg[ \sup_{h \in \mathcal{F}} \bigg( \Big[ \widehat{\mathbb{E}}_{\tilde{S}} \big[ h(z) \big] - \widehat{\mathbb{E}}_S \big[ h(z) \big] \Big] \bigg) \bigg]
\end{split}
\end{equation*}](../../assets/latex/theory_d3aaf6a4ae081c77bd2e212e277393703d6cab8e.png)
Since
![\begin{equation*}
\widehat{\mathbb{E}}_{\tilde{S}} \big[ h(z) \big] - \widehat{\mathbb{E}}_S \big[ h(z) \big] = \frac{1}{m} \sum_{i=1}^{m} \big( h(\tilde{z}_i) - h(z_i) \big)
\end{equation*}](../../assets/latex/theory_840db1d6c6ec177a24db73d3b18015bff58be371.png)
the above is then
![\begin{equation*}
\mathbb{E}_S \Bigg[ \sup_{h \in \mathcal{F}} \bigg( \mathbb{E}_{\tilde{S}} \Big[ \widehat{\mathbb{E}}_{\tilde{S}} \big[ h(z) \big] - \widehat{\mathbb{E}}_S \big[ h(z) \big] \mid S \Big] \bigg) \Bigg] \le \mathbb{E}_{S, \tilde{S}} \Bigg[ \sup_{h \in \mathcal{F}} \bigg( \frac{1}{m} \sum_{i=1}^{m} \Big( h(\tilde{z}_i) - h(z_i) \Big) \bigg) \Bigg]
\end{equation*}](../../assets/latex/theory_43e86ab4ce6def6742fcc3d61f156396f6e5cd6a.png)
This is where the famous Rademacher random variables  , with probability
, with probability  , come in: note that
, come in: note that
![\begin{equation*}
\mathbb{E}_{\sigma, \mathcal{D}} \big[ \sigma f(z) \big] = \mathbb{E}_D \big[ f(z) \big]
\end{equation*}](../../assets/latex/theory_e0f9472b0e7d6d570b91d61dca18c96d7800e265.png)
for any integrable function  . In particular,
. In particular,
![\begin{equation*}
\begin{split}
\mathbb{E}_{S, \tilde{S}} \Bigg[ \sup_{h \in \mathcal{F}} \bigg( \frac{1}{m} \sum_{i=1}^{m} \Big( h(\tilde{z}_i) - h(z_i) \Big) \bigg) \Bigg]
&= \mathbb{E}_{S, \tilde{S}, \sigma} \Bigg[ \sup_{h \in \mathcal{F}} \bigg( \frac{1}{m} \sum_{i=1}^{m} \sigma_i \Big( h(\tilde{z}_i) - h(z_i) \Big) \bigg) \Bigg] \\
&= \mathbb{E}_{S, \tilde{S}, \sigma} \Bigg[ \sup_{h \in \mathcal{F}} \bigg( \frac{1}{m} \sum_{i=1}^{m} \sigma_i h(\tilde{z}_i) + \frac{1}{m} \sum_{i=1}^{m} (- \sigma_i) h(z_i) \bigg) \Bigg] \\
&\le \mathbb{E}_{S, \tilde{S}, \sigma} \Bigg[ \sup_{h \in \mathcal{F}} \bigg( \frac{1}{m} \sum_{i=1}^{m} \sigma_i h(\tilde{z}_i) \bigg) + \sup_{h \in \mathcal{F}} \bigg( \frac{1}{m} \sum_{i=1}^{m} \sigma_i h(z_i) \bigg) \Bigg] \\
&= \mathbb{E}_{\tilde{S}, \sigma} \Bigg[ \sup_{h \in \mathcal{F}} \bigg( \frac{1}{m} \sum_{i=1}^{m} \sigma_i h(\tilde{z}_i) \bigg) \Bigg] + \mathbb{E}_{S, \sigma} \Bigg[ \sup_{h \in \mathcal{F}} \bigg( \frac{1}{m} \sum_{i=1}^{m} \sigma_i h(z_i) \bigg) \Bigg] \\
&= 2 \underbrace{\mathbb{E}_{S, \sigma} \Bigg[ \sup_{h \in \mathcal{F}} \bigg( \frac{1}{m} \sum_{i=1}^{m} \sigma_i h(z_i) \bigg) \Bigg]}_{= R_m(\mathcal{F})} \\
&= 2 R_m(\mathcal{F})
\end{split}
\end{equation*}](../../assets/latex/theory_1b79c56e5a699ba26bc59b7e4de02e4b85061d32.png)
That is, we have now proven that
![\begin{equation*}
\mathbb{E}_S \Bigg[ \sup_{h \in \mathcal{F}} \bigg( \mathbb{E}_D \big[ h(z) \big] - \widehat{\mathbb{E}}_S \big[ h(z) \big] \bigg) \Bigg] \le 2 R_m(\mathcal{F})
\end{equation*}](../../assets/latex/theory_e26bb530bafee9372a816542b034d788c3acd5fe.png)
Finally, combining it all:
![\begin{equation*}
\begin{split}
\mathbb{E}_D \big[ f(z) \big] &\le \widehat{\mathbb{E}}_S \big[ f(z) \big] + \mathbb{E}_S \Bigg[ \sup_{h \in \mathcal{F}} \bigg( \mathbb{E}_D\big[h(z)\big] - \widehat{\mathbb{E}}_S \big[h(z)\big] \bigg) \Bigg] + \sqrt{\frac{\log(1 / \delta)}{m}} \\
&\le \widehat{\mathbb{E}}_S \big[ f(z) \big] + 2 R_m(\mathcal{F}) + \sqrt{\frac{\log(1 / \delta)}{m}}
\end{split}
\end{equation*}](../../assets/latex/theory_1d150dc62547b28ebee748a48a701e5c1efa210a.png)
QED boys.
For each  , we have
, we have
![\begin{equation*}
\mathbb{E}_D \big[ f(z) \big] \le \widehat{\mathbb{E}}_S \big[ f(z) \big] + 2 \hat{R}_m (\mathcal{F}) + 3 \sqrt{\frac{\log (2 / \delta)}{m}}
\end{equation*}](../../assets/latex/theory_6a506794037c9d87f29c46ce8e6ef67c24183509.png)
First notice that  satisfies the necessary conditions of McDiarmid's inequality, and so we immediately have
satisfies the necessary conditions of McDiarmid's inequality, and so we immediately have

for any  . Again we can solve for RHS being less than
. Again we can solve for RHS being less than  , giving us
, giving us
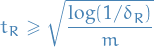
If we denote  the constant obtained for our earlier application of McDiarmid's inequality to bound the difference
the constant obtained for our earlier application of McDiarmid's inequality to bound the difference ![$\varphi(S) - \mathbb{E}_S \big[ \varphi(S) \big]$](../../assets/latex/theory_e4ca303326b414a1bc2d02ab58469901fa9a31c1.png) , we then have
, we then have
![\begin{equation*}
\mathbb{E}_D \big[ f(z) \big] \le \widehat{\mathbb{E}}_S \big[ f(z) \big] + 2 \hat{R}_m(\mathcal{F}) + 2 \sqrt{\frac{\log (1 / \delta_R)}{m}} + \sqrt{\frac{\log (1 / \delta_D)}{m}}
\end{equation*}](../../assets/latex/theory_120dd4e092fdcfe6dc32c4bf486ec7208e3968ce.png)
with probability at least  . Setting
. Setting  , we get
, we get
![\begin{equation*}
\mathbb{E}_D \big[ f(z) \big] \le \widehat{\mathbb{E}}_S \big[ f(z) \big] + 2 \hat{R}_m(\mathcal{F}) + 3 \sqrt{\frac{\log(2 / \delta)}{m}}
\end{equation*}](../../assets/latex/theory_ccfd09d64f53979a40ecd50fe8a95b47678d74c2.png)
with probability at least  , as wanted.
, as wanted.
PAC-Bayesian generalization bounds
- Now consider Bayesian approach where we have a prior on the hypothesis class and using data to arrive at a posterior distribution
Notation
 is a prior distribution on the hypothesis class
is a prior distribution on the hypothesis class 
 posterior distribution over the hypothesis class
posterior distribution over the hypothesis class 
 denotes the KL-divergence of
denotes the KL-divergence of  and
and 
Stuff
- Prediction for input
 is to pick random hypothesis
is to pick random hypothesis  according to
according to  and predict
and predict 
Gives rise to the error
![\begin{equation*}
\underset{h \sim Q}{\mathbb{E}} \big[ L_D(h) \big]
\end{equation*}](../../assets/latex/theory_045653c9ff292e1b376ecbd8f77e903ea1a0daa5.png)
Consider a distribution  on the data. Let
on the data. Let
 be a prior distribution over hypothesis class
be a prior distribution over hypothesis class 

Then with probability  , on a i.i.d. sample
, on a i.i.d. sample 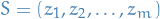 of size
of size  from
from  , for all distributions
, for all distributions  over
over  (which could possibly depend on
(which could possibly depend on  ), we have that
), we have that
![\begin{equation*}
\Delta_S \Big( Q(\mathcal{H}) \Big) = \underset{h \sim Q}{\mathbb{E}} \Big[ L_D(h) \Big] - \underset{h \sim Q}{ \mathbb{E}} \Big[ L_S(h) \Big] \le \sqrt{\frac{D \big( Q || P \big) + \ln m / \delta}{2 (m - 1)}}
\end{equation*}](../../assets/latex/theory_ef9add097892db854b1e6af1f7ef93991317df1a.png)
This is saying that the generalization error is bounded above by the square root of the KL-divergence of the distributions (plus some terms that arise from the "concentration bounds").
From this theorem, in order to minimize the error on the real distribution  , we should try to simultaneously minimize the empirical error as well as the KL-divergence between the posterior and the prior.
, we should try to simultaneously minimize the empirical error as well as the KL-divergence between the posterior and the prior.
Observe that for fixed  , using a standard Hoeffdings inequality, we have that
, using a standard Hoeffdings inequality, we have that
![\begin{equation*}
\underset{S}{\text{Pr}} \big[ \Delta(h) > \varepsilon \big] \le e^{- 2m \varepsilon^2}
\end{equation*}](../../assets/latex/theory_226554d3a4272c5bf96d095c0ecc110e37266e29.png)
which means the generalization error of a given hypothesis exceeds a given constant is exponentially small. Thus, with very high probability, the generalization error is bounded by a small constant. Roughly, this says that 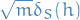 behaves like a univariate gaussian. Using concentration bounds, this further implies that
behaves like a univariate gaussian. Using concentration bounds, this further implies that
![\begin{equation*}
\underset{S}{\mathbb{E}} \Big[ \exp \Big(2 (m - 1) \Delta(h)^2 \Big) \Big] \le m
\end{equation*}](../../assets/latex/theory_307ea30576e3963c8331dd9a1e54fc57ec70e631.png)
and therefore, with high probability over  ,
,

Then consider the expression (which can be obtained by working backwards from the statement of the claim)
![\begin{equation*}
2 ( m- 1) \underset{h \sim Q}{\mathbb{E}} \textcolor{green}{\big[ \Delta (h) \big]^2} - D(Q||P) \le
2 ( m- 1) \underset{h \sim Q}{\mathbb{E}} \textcolor{red}{\big[ \Delta (h)^2 \big]} - D(Q||P)
\end{equation*}](../../assets/latex/theory_d23f8a392f7914ac41490fc490470f71ad1c5bce.png)
where the inequality is by convexity of squares. This in turn is now
![\begin{equation*}
\begin{split}
2 (m - 1) \underset{h \sim Q}{\mathbb{E}} \big[ \Delta (h)^2 \big] - D(Q || P)
&= \underset{h \sim Q}{\mathbb{E}} \Bigg[ 2(m - 1) \Delta(h)^2 - \ln \frac{Q(h)}{P(h)} \Bigg] \\
&= \underset{h \sim Q}{\mathbb{E}} \Bigg[ \ln \Bigg( \exp \Big( 2 (m - 1) \Delta(h)^2 \Big) \frac{P(h)}{Q(h)} \Bigg) \Bigg] \\
&\le \ln \underset{h \sim Q}{\mathbb{E}} \Bigg[ \ln \Bigg( \exp \Big( 2 (m - 1) \Delta(h)^2 \Big) \frac{P(h)}{Q(h)} \Bigg) \Bigg]
\end{split}
\end{equation*}](../../assets/latex/theory_b7f3b25aac172c9f5c98740dbcb8ad31361a707d.png)
where the last inequality uses Jensen's Inequality along with the concavity of  . Also, we have
. Also, we have
![\begin{equation*}
\ln \underset{h \sim Q}{\mathbb{E}} \Bigg[ \Bigg( \exp \Big( 2 (m - 1) \Delta(h)^2 \Big) \frac{P(h)}{Q(h)} \Bigg) \Bigg] = \ln \underset{h \sim P}{\mathbb{E}} \Big[ \exp \big( 2 (m - 1) \Delta(h)^2 \big) \Big]
\end{equation*}](../../assets/latex/theory_e3f07a631644090d56e188bc21d071624b341a44.png)
where the last step is a standard trick; using the KL-divergence term to switch the distribution over which expectation is taken (same as used in Importance Sampling).
Hence,
![\begin{equation*}
2 (m - 1) \underset{h \sim Q}{\mathbb{E}} \big[ \Delta(h) \big]^2 - D(Q || P) \le \ln \bigg( \underset{h \sim P}{\mathbb{E}} \Big[ \exp \big( 2 (m - 1) \Delta(h)^2 \big) \Big] \bigg)
\end{equation*}](../../assets/latex/theory_a1b5818dde1d85f3f7844f2021265b42c4301ecd.png)
Now, substituting this what we found earlier
![\begin{equation*}
\underset{S}{\mathbb{E}} \Bigg[ \underset{h \sim P}{\mathbb{E}} \Big[ \exp \Big( 2 (m - 1) \Delta(h)^2 \Big) \Big] \Bigg] = \mathbb{E}_{h \sim P} \Bigg[ \underset{S}{\mathbb{E}} \Big[ \exp \Big( 2 (m- 1) \Delta(h)^2 \Big) \Big] \Bigg]
\end{equation*}](../../assets/latex/theory_208c332fe1e17ce59b2a98b81c0fce6b31cd684d.png)
since  is independent of
is independent of  . This then implies (again, from what we found above)
. This then implies (again, from what we found above)
![\begin{equation*}
\underset{h \sim P}{\mathbb{E}} \Big[ \exp \Big( 2(m - 1) \Delta(h)^2 \Big) \Big] = \mathcal{O}(m)
\end{equation*}](../../assets/latex/theory_8f4b3770e6548290f47917b5c1627bda86c9b30c.png)
Combining the two previous expressions
![\begin{equation*}
\begin{split}
2(m - 1) \underset{h \sim Q}{\mathbb{E}} \Big[ \Delta(h) \Big]^2 - D(Q || P)
& \le \mathcal{O} \Big( \ln (m) \Big) \\
\implies \underset{h \sim Q}{\mathbb{E}} \Big[ \Delta(h) \Big]^2 & \le \frac{\mathcal{O} \big( \ln(m) \big) + D(Q || P)}{2 (m - 1)} \\
\underset{h \sim Q}{\mathbb{E}} \Big[ \Delta(h) \Big] & \le \sqrt{\frac{\mathcal{O} \big( \ln(m) \big) + D(Q || P)}{2 (m - 1)}}
\end{split}
\end{equation*}](../../assets/latex/theory_5f61b20fb1fa24661b8a8ebc5c58f8bd0455ad52.png)
as claimed!
Appendix
Measure Concentration
Let  be a rv. that takes values in
be a rv. that takes values in ![$[0, 1]$](../../assets/latex/theory_68c8fa38d960e53d4308cbf1e65d04c66a554817.png) . Assume that
. Assume that ![$\mathbb{E}[Z] = \mu$](../../assets/latex/theory_076c625183dcdf30f19008275058e9c8b636988e.png) . Then, for any
. Then, for any  ,
,
![\begin{equation*}
\mathbb{P} \big[ Z > 1- a \big] \ge \frac{\mu - (1 - a)}{a}
\end{equation*}](../../assets/latex/theory_9fcbb2fce5ca3e50b76bc47c27293b7ca3b4d688.png)
This also implies that for every  :
:
![\begin{equation*}
\mathbb{P} \big[ Z > a \big] \ge \frac{\mu - a}{1 - a} \ge \mu - a
\end{equation*}](../../assets/latex/theory_5be5257fd0e4b45b018107bdc36fb6d49c992f46.png)
Bibliography
Bibliography
- [shalev2014understanding] Shalev-Shwartz & Ben-David, Understanding machine learning: From theory to algorithms, Cambridge university press (2014).