Recursive Bayesian Filtering

Table of Contents

Notation

Kalman Filter

Assumed model

We assume the state to be random variable $\mathbf{x}_k$ as follows:

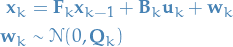\begin{equation*} \begin{split} \mathbf{x}_k &= \mathbf{F}_k \mathbf{x}_{k-1} + \mathbf{B}_k \mathbf{u}_k + \mathbf{w}_k \\ \mathbf{w}_k &\sim \mathcal{N}(0, \mathbf{Q}_k) \end{split} \end{equation*} 1

and the measurements or observations to be a random variable $\mathbf{z}_k$:

\begin{equation*} \begin{split} \mathbf{z}_k &= \mathbf{H}_k \mathbf{x}_k + \mathbf{v}_k \\ \mathbf{v}_k &\sim \mathcal{N}(0, \mathbf{R}_k) \end{split} \end{equation*} 2

I.e. both state $\mathbf{x}_k$ and measurement $\mathbf{z}_k$ are assumed to be normally distributed with covariance-matrices $\mathbf{Q}_k$ and $\mathbf{R}_k$, respectively.

Deduction

Notation

  • $\mathbf{x}_k$ state
  • $\hat{ \mathbf{x} }_k$ predicted state
  • $\mathbf{P}_k$ covariance matrix for the predicted state
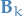  • $\mathbf{B}_k$ control-matrix, e.g. mapping external forces to how it affects the state
  • $\mathbf{u}_k$ control-vector, e.g. external force
  • $\mathbf{Q}_k$ covariance matrix describing external uncertainty from the environment
  • $\mathbf{H}_k$ maps the predicted state to the measurement-space, i.e. "predict" measurement from state
  • $\mathbf{z}_k$ real measurement
  • $\mathbf{R}_k$ uncertainty in real measurements

Algorithm

We start out by writing the predicted state $\hat{\mathbf{x}}_k$ as a function of the previous $\hat{\mathbf{x}}_{k-1}$ predicted state:

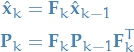\begin{equation*} \begin{split} \hat{\mathbf{x}}_k &= \mathbf{F}_k \hat{\mathbf{x}}_{k-1} \\ \mathbf{P}_k &= \mathbf{F}_k \mathbf{P}_{k-1} \mathbf{F}_k^T \end{split} \end{equation*} 3

Where $\mathbf{P}_k$ is due to the following identify:

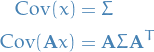\begin{equation*} \begin{split} \text{Cov}(x) &= \Sigma \\ \text{Cov}(\mathbf{A} x) &= \mathbf{A} \Sigma \mathbf{A}^T \end{split} \end{equation*} 4

I.e. mapping the covariance at step $k-1$ to the covariance of the state at step $k$.

The next step is then to incorporate "external forces", where we use:

  • $\mathbf{u}_k$ - control vector which defines how
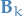  • $\mathbf{B}_k$ - the matrix

I like to view $\mathbf{B}_k \mathbf{u}_k$ as a simple function mapping the control-vector $\mathbf{u}_k$ to the state-space, or rather, a function which maps the external "force" to how this "force" affects the state.

This, together with the uncertainty of the external "forces" / influences:

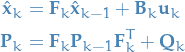\begin{equation*} \begin{split} \hat{\mathbf{x}}_k &= \mathbf{F}_k \hat{\mathbf{x}}_{k-1} + \mathbf{B}_k \mathbf{u}_k \\ \mathbf{P}_k &= \mathbf{F}_k \mathbf{P}_{k-1} \mathbf{F}_k^T + \mathbf{Q}_k \end{split} \end{equation*} 5

Now, what if we can see the real measurement for step $k$, $\mathbf{z}_k$, before proceeding? Well, we would like to update our model! To do this, we need to relate the predicted state to the real state . We thus write the predicted measurement as:

\begin{equation*} \hat{\mathbf{z}}_k = \mathbf{H}_k \hat{\mathbf{x}}_k \end{equation*} 6

Now, we can then write the real measurement as follows:

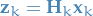\begin{equation*} \mathbf{z}_k = \mathbf{H}_k \mathbf{x}_k \end{equation*} 7

And we of course want the following to be true:

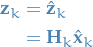\begin{equation*} \begin{split} \mathbf{z}_k &= \hat{\mathbf{z}}_k \\ &= \mathbf{H}_k \hat{\mathbf{x}}_k \end{split} \end{equation*} 8

Therefore we can map the predicted state to the measurement-space by using the matrix $\mathbf{H}_k$.

Thus we have a model for making the predictions, now we need to figure out how to update our model!

For this we first map our "internal" state $\hat{\mathbf{x}}_k$ to the measurement-space. In this case, our measurements only consists of the position $p_k$.

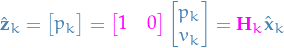
\begin{equation*} \hat{\mathbf{z}}_k = \begin{bmatrix} p_k \end{bmatrix} = \textcolor{magenta}{\begin{bmatrix} 1 & 0 \end{bmatrix}} \begin{bmatrix} p_k \\ v_k \end{bmatrix} = \textcolor{magenta}{\mathbf{H}_k} \hat{\mathbf{x}}_k \end{equation*}

Thus, the predicted measurements follow $\hat{\mathbf{z}}_k \sim \mathcal{N} \big( \textcolor{magenta}{\mathbf{H}_k} \hat{\mathbf{x}}_k, \textcolor{magenta}{\mathbf{H}_k} \mathbf{P}_k \textcolor{magenta}{\mathbf{H}_k^T} \big)$ and the real measurements follow $\mathbf{z}_k \sim \mathcal{N} \big(\textcolor{Magenta}{\mathbf{H}_k} \mathbf{x}_k, \textcolor{magenta}{\mathbf{R}_k} \big)$, where $\mathbf{x}_k$ is the "real" internal state.

To compute our updated state, we can then take the joint distribution of the predicted and real measurements, incorporating information from both our estimate and the current measurement.

Due to the joint-probability of two Gaussian rvs. also being Guassian, with mean $\mu$ and covariance $\Sigma$

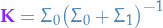
\begin{equation*} \textcolor{Purple}{\mathbf{K}} = \Sigma_0 \big( \Sigma_0 + \Sigma_1 \big)^{-1} \end{equation*}
\begin{equation*} \mu = \mu_0 + \textcolor{Purple}{\mathbf{K}} \big( \mu_1 - \mu_0 \big) \end{equation*}
\begin{equation*} \Sigma = \big( \mathbf{I} - \textcolor{Purple}{\mathbf{K}} \big) \Sigma_0 \end{equation*}

In the context of Kalman filters we call 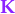$\textcolor{Purple}{\mathbf{K}}$ the Kalman gain.

By letting $\big( \mu_0, \Sigma_0 \big) = \big( \mathbf{H}_k \hat{\mathbf{x}}_k \big)$ and $\big( \mu_1, \Sigma_1 \big) = \big( \mathbf{z}_k, \mathbf{R}_k \big)$, we get the update-equations:

\begin{equation*} \hat{\mathbf{x}}_k' = \hat{\mathbf{x}}_k + \mathbf{K}' \big( \mathbf{z}_k - \mathbf{H}_k \hat{\mathbf{x}}_k \big) \end{equation*}
\begin{equation*} \mathbf{P}_k' = \mathbf{P}_k - \mathbf{K}' \mathbf{H}_k \mathbf{P}_k \end{equation*}

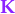where $\mathbf{K}'$ is $\textcolor{Purple}{\mathbf{K}}$ without the $\mathbf{H}_k$ in front.

Summary

Predict!

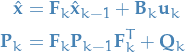\begin{equation*} \begin{split} \hat{\mathbf{x}} &= \mathbf{F}_k \hat{\mathbf{x}}_{k-1} + \mathbf{B}_k \mathbf{u}_k \\ \mathbf{P}_k &= \mathbf{F}_k \mathbf{P}_{k-1} \mathbf{F}_k^T + \mathbf{Q}_k \end{split} \end{equation*} 9

Update! Since our predictive model is Gaussian, and we assume a Gaussian distribution for our measurements, we simply update our model parameters $\hat{\mathbf{x}}_k, \mathbf{P}_k$ by taking the joint-distribution of these two Gaussian rvs., which again gives us a Guassian distribution with the new updated paramters:

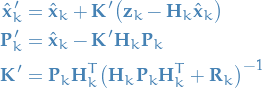\begin{equation*} \begin{split} \hat{\mathbf{x}}_k' &= \hat{\mathbf{x}}_k + \mathbf{K}' \big( \mathbf{z}_k - \mathbf{H}_k \hat{\mathbf{x}}_k \big) \\ \mathbf{P}_k' &= \hat{\mathbf{x}}_k - \mathbf{K}' \mathbf{H}_k \mathbf{P}_k \\ \mathbf{K}' &= \mathbf{P}_k \mathbf{H}_k^T \big( \mathbf{H}_k \mathbf{P}_k \mathbf{H}_k^T + \mathbf{R}_k \big)^{-1} \end{split} \end{equation*} 10

Prediction

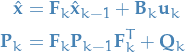\begin{equation*} \begin{split} \hat{\mathbf{x}} &= \mathbf{F}_k \hat{\mathbf{x}}_{k-1} + \mathbf{B}_k \mathbf{u}_k \\ \mathbf{P}_k &= \mathbf{F}_k \mathbf{P}_{k-1} \mathbf{F}_k^T + \mathbf{Q}_k \end{split} \end{equation*} 11

Update

Since our predictive model is Gaussian, and we assume a Gaussian distribution for our measurements, we simply update our model parameters $\hat{\mathbf{x}}_k, \mathbf{P}_k$ by taking the joint-distribution of these two Gaussian rvs., which again gives us a Guassian distribution with the new updated parameters:

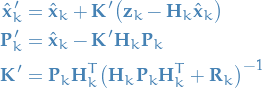\begin{equation*} \begin{split} \hat{\mathbf{x}}_k' &= \hat{\mathbf{x}}_k + \mathbf{K}' \big( \mathbf{z}_k - \mathbf{H}_k \hat{\mathbf{x}}_k \big) \\ \mathbf{P}_k' &= \hat{\mathbf{x}}_k - \mathbf{K}' \mathbf{H}_k \mathbf{P}_k \\ \mathbf{K}' &= \mathbf{P}_k \mathbf{H}_k^T \big( \mathbf{H}_k \mathbf{P}_k \mathbf{H}_k^T + \mathbf{R}_k \big)^{-1} \end{split} \end{equation*} 12

Particle Filtering

Notation

  • $x_k^{(i)}$ denotes the k-th sampled step of the i-th "particle" / sample-sequence
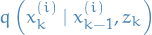  • $q\left(x_{k}^{(i)} \mid x_{k - 1}^{(i)}, z_k \right)$ is the "importance distribution" which we can sample from

Overview

  • Can represent arbitrary distributions
    • But this is an approximate method, unlike method such as Kalman Filter which are (asymptotically) exact and "optimal"
  • Name comes from the fact that we're keeping track of multiple "particles"
    • "Particle" is just a single "chain" of samples
  • Main building-block is Importance Sampling (IS)
    • "Extended" to sequences, which we call Sequential Importance Sampling

Sequential Importance Sampling (SIS)

Sequential Importance Sampling (SIS) extends Importance Sampling (IS) by updating the sample-weights $w_k^{(i)}$ sequentially.

The particle and weight updates, respectively, are defined by

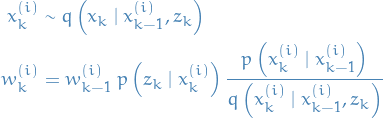
\begin{equation*} \begin{split} x_k^{(i)} & \sim q\left(x_k \mid x_{k-1}^{(i)}, z_k \right) \\ w_k^{(i)} & = w_{k - 1}^{(i)} \ p \left(z_k \mid x_k^{(i)} \right) \frac{p \left(x_k^{(i)} \mid x_{k - 1}^{(i)} \right)}{q \left(x_k^{(i)} \mid x_{k - 1}^{(i)}, z_k \right)} \end{split} \end{equation*}

IMPORTANT: normalize the weights after each weight-update, such that we can use the weights to approximate the expectations.

\begin{equation*} \mathbb{E}[f(x_k)] = \frac{1}{N} \sum_{i=1}^{N} w_k^{(i)} f \left( x_k^{(i)} \right) \end{equation*}

Degeneracy phenomenon

  • Usually after a few iterations of SIS most particles have neglible weights
    • => large computation efforts for updating particles with very small contributions: highly inefficient

  • One can "measure" degeneracy using the "effective sample size":

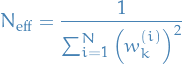
    \begin{equation*} N_{\text{eff}} = \frac{1}{\sum_{i=1}^{N} \left( w_k^{(i)} \right)^2 } \end{equation*}
    • Uniform: $N_{\text{eff}} = N$
    • Severe degeneracy: $N_{\text{eff}} = 1$
  • To deal with degeneracy we introduce resampling
  1. When degeneracy is above a threshold, eliminate particles with low importance weights

  2. Sample $N$ new samples / "particles" $\{ \tilde{x}_k^{(i)} \}$ by

    \begin{equation*} \begin{split} j &\sim \text{Categorical} \left( w_k^{(1)}, \dots, w_k^{(N)} \right) \\ \tilde{x}_k^{(i)} & := x_k^{(j)} \end{split} \end{equation*}

    i.e. we're generating new particles by drawing from the current particles, each with probability equal to the corresponding weight.

    • If we eliminiated the particles with low importance weights, the corresponding weights should of course not be included.

  3. New samples and weights are

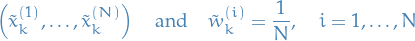
    \begin{equation*} \left( \tilde{x}_k^{(1)}, \dots, \tilde{x}_k^{(N)} \right) \quad \text{and} \quad \tilde{w}_k^{(i)} = \frac{1}{N}, \quad i = 1, \dots, N \end{equation*}

    i.e. new weights are uniform.

A good threshold is a "measure" of degeneracy using the "effective sample size":

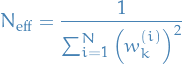
\begin{equation*} N_{\text{eff}} = \frac{1}{\sum_{i=1}^{N} \left( w_k^{(i)} \right)^2 } \end{equation*}
  • Uniform: $N_{\text{eff}} = N$
  • Severe degeneracy: $N_{\text{eff}} = 1$

Practical considerations

Implementing the categorical sampling method used in resampling can efficiently be performed by

  1. Normalize weights
  2. Calculate an array of the cumulative sum of the weights
    • Partitions the range $[0, 1]$ into $N$ intervals
    • If $u \sim \text{Uniform}$, then the interval $u$ falls into is the corresponding $x_k^{(i)}$
  3. Randomly generate $N$ uniform numbers $\{ u_i \}$ and determine the corresponding samples

Generic Particle Filtering

Combining SIS and resampling, we get generic Particle Filtering.

At each "step" $k$, we "obtain new states" / "update the particles" through:

  1. Produce tuple of samples $\left(x_k^{(1)}, \dots, x_k^{(N)} \right)$ using SIS
  2. Compute $N_{\text{eff}}$
    • If $N_{\text{eff}} < N_{\text{thr}}$: resample!