Normalizing flows

Table of Contents

Literature

Results

"Why the name?!"

I've received this question or a similar one on more than one occation. Normalizing flows is really not a good name for what it is supposed to represent. It is also unclear whether or not it refers to the base distribution together with the transformation, or just the transformation itself, ignoring the base distribution which is transformed.

I've received questions such as

  • "Is this related to gradient flows in differential equations and manifolds?" which is a completely valid question because that is indeed what it sounds like it is! I'd say something like "Well, kind of, but also not really. A gradient flow could technically be used in a normalizing flow but it's way too strict of an requirement; you really just need a differentiable bijection with a differentiable inverse. A gradient flow is indeed this (at least locally), but yeah, you can also just have, say, addition by a constant factor."

Today, I'd say a normalizing flow is a piecewise [[file:..mathematicsgeometry.org::def:diffeomorphism][diffeomorphic]] [[file:..mathematicsmeasuretheory.org::def:push-forward-measure][push-forward]], or in simpler terms, it's a differentiable function 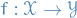$f: \mathcal{X} \to \mathcal{Y}$ with a differentiable inverse 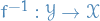$f^{-1}: \mathcal{Y} \to \mathcal{X}$ together with a base distribution $P$ on $\mathcal{X}$ with a density $p: \mathcal{X} \to [0, 1]$.

So, why isn't it just called a this? It seems like the term normalizing flows was popularized in 2014 by rezende15_variat_infer_with_normal_flows. This paper refers to the "method of normalizing flows" from tabak2010density in which we can probably find the first use of the term. In this work they do the following

  1. Define

    \begin{equation*} \rho(x) = \mu \big( y(x) \big) \left| \mathcal{J}_y(x) \right| \end{equation*}

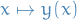    where $\mu(y)$ is a known density and $\mathcal{J}_y(x)$ denotes the Jacobian of the map $x \mapsto y(x)$.

  2. Define the mapping $y(x)$ as an "infinite composition of infinitesimal transformations", i.e. a (gradient) flow $z_t = \phi_t(x)$ s.t.

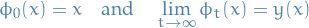
    \begin{equation*} \phi_0(x) = x \quad \text{and} \quad \lim_{t \to \infty} \phi_t(x) = y(x) \end{equation*}

  3. Define

    \begin{equation*} \tilde{\rho}_t(x) = \mu \big( \phi_t(x) \big) \mathcal{J}_{\phi_t}(x) \end{equation*}

    then

    \begin{equation*} \tilde{\rho}_0(x) = \mu(x) \quad \text{and} \quad \lim_{t \to \infty} \tilde{\rho}_t(x) = \rho(x) \end{equation*}

  4. Given a set of samples $\left\{ x^j \right\}_{j = 1}^m$, we can measure the quality of the estimated density $\tilde{\rho}_t(x)$ by the log-likelihood, treating it as a functional on $\phi_t$:

    \begin{equation*} L[\phi_t] = \frac{1}{m} \sum_{j=1}^{m} \log \tilde{\rho}_t(x^j) \end{equation*}

    This suggests constructing the flow $\phi_t$ by following the direction of ascent of $\mathcal{L}[\phi_t]$, i.e. s.t.

    \begin{equation*} \dv{}{t} L[\phi_t] \ge 0 \end{equation*}

    and such that $y(x) = \lim_{t \to \infty} \phi_t(x)$ is the (local) minimizer.

\begin{equation*} \dv{z}{t} = \frac{1}{\mu(z)} \rho_t(z) \big( \nabla_z \mu(z) \big) - \nabla_z \rho_t(z) \end{equation*}

where

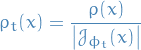
\begin{equation*} \rho_t(x) = \frac{\rho(x)}{\left| \mathcal{J}_{\phi_t}(x) \right|} \end{equation*}

Note that

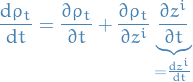
\begin{equation*} \dv{\rho_t}{t} = \pdv{\rho_t}{t} + \pdv{\rho_t}{z^i} \underbrace{\pdv{z^i}{t}}_{= \dv{z^i}{t}} \end{equation*}

In this work they describe a method of defining a (gradient) flow

Basically, in this work they define a gradient flow using the log-likelihood which transforms from a known density $\mu$ to the unknown density $\rho$. They also consider the dual of the flow, which transforms from $\rho$ to $\mu$, which they refer to as "transforming $\rho$ to normality", i.e. a normalizing flow in the sense that it's a flow which transforms a density to normality / a normal distribution. For practical purposes they consider "infinitesimal" small additive changes, which is basically what we today refer to as residual normalizing flows behrmann18_inver_resid_networ. They also point out that the work of "Gaussianization" which was done in 2002 follow a similar idea, though not using flows.