LDA: Latent Dirichlet Allocation
Table of Contents
Motivation
Bag-of-words models in general performs quite well, and we're looking for a probabilistic model of text. Let's look at the underlying assumptions of a bag-of-word model:
- Ordering of words within a document is irrelevant
- Ordering of documents in entire corpus is irrelevant
In probability we call this exchangebility. You remember anything about this? [BROKEN LINK: No match for fuzzy expression: *Dirichlet%20process] maybe?!
Notation
- word is the basic unit of discrete data, defined to be an item
from a vocabulary indexed by
 .
Represented using unit-basis vectors that have a single component
equal to 1 and all other components equal to 0. Thus, using superscripts
to denote components,the
.
Represented using unit-basis vectors that have a single component
equal to 1 and all other components equal to 0. Thus, using superscripts
to denote components,the  word in the vocabulary is
represented by a V-vector
word in the vocabulary is
represented by a V-vector  such that
such that  and
and 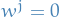 for
for  .
. - document is a sequence of
 words denoted by
words denoted by  where
where 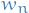 is the
is the  word in the sequence
word in the sequence - corpus is a collection of
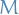 documents denoted by
documents denoted by  .
. - topic is characterized by a distribution over words
Latent Dirichlet Allocation
- Generative model of a corpus
- Documents are represented as a random mixtures over latent topics
Notation
 parameter for Dirichlet distribution
parameter for Dirichlet distribution latent random variable for some document (
latent random variable for some document ( for a specific document
for a specific document  )
drawn from a
)
drawn from a 
 is a k-dimensional one-hot-vector representing the chosen topic for a word
i.e. with the i-th component equal to 1 and all other components being 0 (
is a k-dimensional one-hot-vector representing the chosen topic for a word
i.e. with the i-th component equal to 1 and all other components being 0 (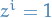 for a unique
for a unique  )
)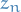 is the same as
is the same as  , but for the specific n-th word
, but for the specific n-th word 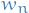 in a document, i.e. topic for this word.
in a document, i.e. topic for this word. is a
is a  matrix parameterizing the word probabilities,
i.e.
matrix parameterizing the word probabilities,
i.e. 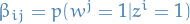
Model
Assume the following generative model for each document  in a corpus
in a corpus  :
:
- Choose
 , i.e. the length of the document
(following this distribution is not a strict requirement)
, i.e. the length of the document
(following this distribution is not a strict requirement) - Choose
 , used as a parameter for a multinomial later on
, used as a parameter for a multinomial later on - Each word
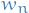 in the document of length
in the document of length  is assigned as follows:
is assigned as follows:
- Choose a topic

- Choose a word
 , multinomial distribution conditioned
on the topic
, multinomial distribution conditioned
on the topic 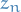
- Choose a topic
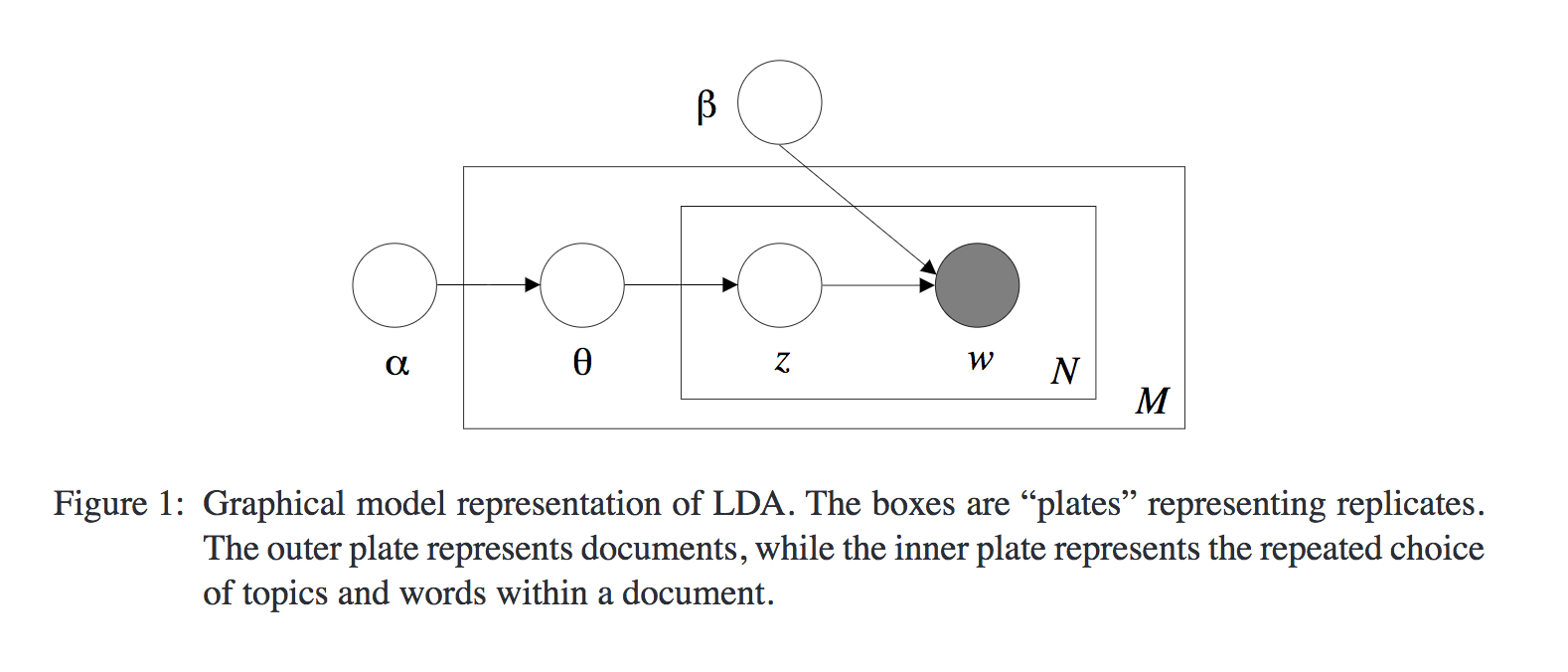
Dirichlet
My interpretation
From a Dirichlet we draw a  -vector which corresponds to a multinomial distribution,
with each component corresponding to the probability of the corresponding topic / label / class.
In our case,
-vector which corresponds to a multinomial distribution,
with each component corresponding to the probability of the corresponding topic / label / class.
In our case,  then corresponds to the i-th component of
then corresponds to the i-th component of  ,
i.e. the probability of topic
,
i.e. the probability of topic  .
.
From the paper
A k-dimensional Dirichlet random variable  can take values in the (k−1)-simplex
(a k-vector
can take values in the (k−1)-simplex
(a k-vector  lies in the (k − 1)-simplex if
lies in the (k − 1)-simplex if 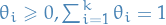 ),
and has the following probability density on this simplex:
),
and has the following probability density on this simplex:
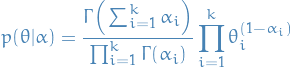 1
1
When we're talking about the (k - 1)-simplex we're referring to a region of space where
the parameters of the mutlinomial can be (domain of all  ). Why
). Why  ?
Since we require that the sum over all
?
Since we require that the sum over all  equals 1, after choosing a value for
equals 1, after choosing a value for  of these, the last one is determined as
of these, the last one is determined as  .
.
The  and
and  being referred to in this section on the Dirichlet has nothing to do with
notation used elswhere in this text, and simply represents some arbitrary integer
being referred to in this section on the Dirichlet has nothing to do with
notation used elswhere in this text, and simply represents some arbitrary integer  and some random variable
and some random variable  .
.
Joint distributions
First we have the joint distribution over the topic mixture  , topics
, topics  and words
and words  for one document:
for one document:
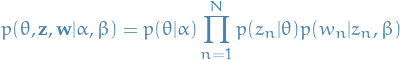 2
2
Where  where
where  since
since 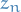 is a one-hot vector representing the
n-th chosen topic.
is a one-hot vector representing the
n-th chosen topic.
topic mixture simply refers to a latent variable which the rv. topic depends on.
Then to obtain the probability of a document  , i.e. a set of words
, i.e. a set of words  ,
we simply integrate over all topic mixtures
,
we simply integrate over all topic mixtures  and summing over all possible
topic assignments
and summing over all possible
topic assignments 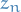
 3
3
And finally, to obtain the distribution over our corpus, i.e. our set of documents, we simply take the product over all documents
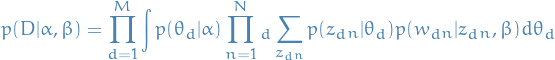 4
4
Inference
Our inference problem is to compute the distributions of the latent variables  and
and  given a document
given a document  .
.
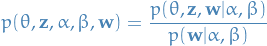 5
5
Both of which we deduced in the previous section! Unfortunately, this computation is intractable. Luckily there exists methods to deal with this: variational inference, MCMC and Laplace approximation.