Graphical models
Table of Contents
Notation
 denotes the parent nodes of the rv.
denotes the parent nodes of the rv.  in the BN
in the BN denotes a clique
denotes a clique denotes a set of variables in the clique
denotes a set of variables in the clique 
 are potential functions
are potential functions
Markov Random Fields
A Markov random field, also known as a Markov network or an undirected graphical model, has a set of nodes each of which corresponds to a variable or group of variables, as well as a set of links each of which connects a pair of nodes.
The links are undirected, i.e. do not carry arrows.
The Markov blanket of a node in a graphical model contains all the variables that "shield" the node from the rest of the network.
What this really means is that every set of nodes in a graphical model is conditionally independent of 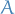 when conditioned on the set
when conditioned on the set  , where
, where  denotes the Markov blanket of
denotes the Markov blanket of 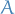 ; formally for distinct nodes
; formally for distinct nodes 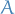 and
and 

In a Bayesian network,  is simply the set of nodes consisting of:
is simply the set of nodes consisting of:
- parents of
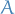
- children of
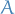
- parents of children of
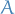 (these nodes are sometimes referred to has having a "explaining-away" effect)
(these nodes are sometimes referred to has having a "explaining-away" effect)
Belief Network
A belief network is a distribution of the form
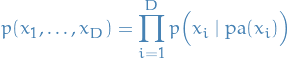
where  denotes the parental variables of variable
denotes the parental variables of variable 
This can be written as a DAG, with the i-th node in the graph corresponding to the factor  .
.
Factorization properties
- Without loss of generality, only consider maximal cliques, since all other cliques are subsets
The joint distribution is written as a product of potential functions  over the maximal cliques of the graph
over the maximal cliques of the graph
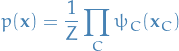
where the partition function is given by
which ensures that the distribution  is correctly normalized.
is correctly normalized.
To make a formal connection between the conditional independence and factorization for undirected graphs, we restrict attention to potential functions  that are strictly positive, thus we can express them as:
that are strictly positive, thus we can express them as:

where  is called the energy function , and the exponential representation is called the Boltzmann distribution or Gibbs distribution.
is called the energy function , and the exponential representation is called the Boltzmann distribution or Gibbs distribution.
A graph is said to be a D map (for dependency map) of a distribution if every conditional indepedence statement satisfied by the distribution is reflected in the graph.
Thus a completely disconnected graph (no links) wil l be a trivial D map for any distribution.
A graph is said to be a I map (for independence map) if every conditional independence statement implied by the graph is satisfied by a specific distribution.
Clearly a fully connected graph will be a trivial I map for any distribution.
If is the case that every conditional independence property of the distribution is reflected in the graph, and vice versa, then graph is said to be a perfect map.
Inference in Graphical Models
Notation
 denotes a variable (can be scalar, vector, matrices, etc.)
denotes a variable (can be scalar, vector, matrices, etc.) denotes a subset of variables
denotes a subset of variables 
 denotes the set of factor nodes that are neighbours of
denotes the set of factor nodes that are neighbours of 
 denotes the set of variables in the subtree connected to the variable node
denotes the set of variables in the subtree connected to the variable node  via a factor node
via a factor node 
 denotes the set of variables in the subtree connected to the variable node
denotes the set of variables in the subtree connected to the variable node  via a factor node
via a factor node 
- f
 depends on
depends on  , which we denote
, which we denote 
 represents the product of all the factors in the group associated with factor
represents the product of all the factors in the group associated with factor 
Message from factor node
 to variable node
to variable node  :
:
Message from variable node
 to factor node
to factor node  :
:
where
 denotes the set of factors in the subtree connected to the factor node
denotes the set of factors in the subtree connected to the factor node  via the variable node
via the variable node 
Factor graphs
Can write joint distribution over a set of variables in the form of a product of factors
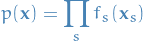
where
 denotes a subset of the variables.
denotes a subset of the variables.
- Directed graphs represent special cases in which factors
 are local conditional distributions
are local conditional distributions - Undirect graphs are a special case in which factors are potential functions over the maximal cliques (the normalizing coefficient
 can be viewed as a factor defined over the empty set of variables)
can be viewed as a factor defined over the empty set of variables)
Converting distribution expressed in terms of undirected graph to factor graph
- Create variable nodes corresponding to the nodes in the original undirected graph
- Create additional factor nodes corresponding to the maximal cliques

- Factors
 are set equal to the clique potentials
are set equal to the clique potentials 
There might be several factor graphs corresponding to the same undirected graph, i.e. this construction is not unique.
Sum-product algorithm
- Problem: evaluate local marginals over nodes or subsets of nodes
- Applicable to tree-structured graphs
- Exploit structure of the graph to achieve:
- efficient, exact inference algorithm for finding marginals
- in situations where several marginals are required to allow computations to be shared efficiently
- Summarized: barber2012


Belief propagation is a special case of sum-product algorithm, which performs exact inference on directed graphs without loops. (You have already written about this)
For actual implementation it's useful to use the logarithmic version of the messages. See barber2012.
Derivation
Marginal is obtained by summing the joint distribution over all variables except
 so that
so that
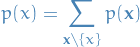
where
 denotes the set of variables in
denotes the set of variables in  with the variable
with the variable  omitted.
omitted.
Joint distribution of the set of variables
 can be written as a product of the form
can be written as a product of the form

Rewriting the marginal above using the joint distribution notation:
![\begin{equation*}
\begin{split}
p(x) &= \prod_{s \in \text{ne}(x)} \Bigg[ \sum_{X_s} F_s(x, X_s) \Bigg] \\
&= \prod_{s \in \text{ne}(x)} \mu_{f_s \to x}(x)
\end{split}
\end{equation*}](../../assets/latex/graphical_models_b2ec044a3d4700dfce208b842605adccda639fa6.png)
i.e. marginal is given by the product of all incoming messages arriving at node
 .
.
Each factor
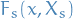 can be descrbied by a factor (sub-)graph and so can itself be factorized:
can be descrbied by a factor (sub-)graph and so can itself be factorized:

where, for convenience, we have denoted the variable associated with factor
 , in addition to
, in addition to  , by
, by  .
.
Message
 to
to  can be rewritten:
can be rewritten:
![\begin{equation*}
\begin{split}
\mu_{f_s \to x} (x) & = \sum_{x_1} \dots \sum_{x_M} f_s(x, x_1, \dots, x_M) \prod_{m \in \text{ne}(f_s) \setminus x} \Bigg[ \sum_{X_{xm}} G_m(x_m, X_{sm}) \Bigg] \\
&= \sum_{x_1} \dots \sum_{x_M} f_s(x, x_1, \dots, x_M) \prod_{m \in \text{ne}(f_s) \setminus x} \mu_{x_m \to f_s}(x_m)
\end{split}
\end{equation*}](../../assets/latex/graphical_models_ed38558fbf9f5ab743f19ce60843b8599c35b751.png)
i.e. marginalizing over all the variables which
 depend on, and the "messages" which are being sent from the variables to the factor
depend on, and the "messages" which are being sent from the variables to the factor  . Thus, to evaluate message sent by factor to variable along the link connceting them:
. Thus, to evaluate message sent by factor to variable along the link connceting them:
- Take product of incoming messages along all other links coming into the factor node
- Multiply by the factor associated with that node
- Marginalize over all of the variables associated with the incoming messages
Message
 to
to  can be written:
can be written:
![\begin{equation*}
\begin{split}
\mu_{x_m \to f_s}(x_m) &= \prod_{l \in \text{ne}(x_m) \setminus \left\{ f_s \right\}} \Bigg[ \sum_{X_{ml}} F_l(x_m, X_{ml}) \Bigg] \\
&= \prod_{l \in \text{ne}(x_m) \setminus \left\{ f_s \right\}} \mu_{f_l \to x_m}(x_m)
\end{split}
\end{equation*}](../../assets/latex/graphical_models_3226a6e5accea75ba4dc8de769bf7b441a1333a0.png)
i.e. to evaluate messages passed from variables to adjacent factors we simply take the product of incoming messages the incoming messages along all other links.
- Messages can be computed recursively
- Start: if leaf-node is:
variable: message it sends along its one and only link is given by

factor: message it sends is simply
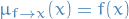
- Start: if leaf-node is:
Finally, if we wish to find the marginal distributions
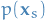 associated with the sets of variables belonging to each factors:
associated with the sets of variables belonging to each factors:

Summarized
The sum-product algorithm can then be summarized as:
- Variable node
 is chosen as root of the factor graph
is chosen as root of the factor graph - Messages are initiaed at the leaves of the graph, if leaf is:
variable: message it sends along its one and only link is given by

factor: message it sends is simply
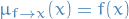
Message passing steps are applied recursively until messages have been propagated along every link:
![\begin{equation*}
\begin{split}
\mu_{f_s \to x} (x) & = \sum_{x_1} \dots \sum_{x_M} f_s(x, x_1, \dots, x_M) \prod_{m \in \text{ne}(f_s) \setminus x} \Bigg[ \sum_{X_{xm}} G_m(x_m, X_{sm}) \Bigg] \\
&= \sum_{x_1} \dots \sum_{x_M} f_s(x, x_1, \dots, x_M) \prod_{m \in \text{ne}(f_s) \setminus x} \mu_{x_m \to f_s}(x_m) \\
&= \sum_{X_s} F_s(x, X_s)
\end{split}
\end{equation*}](../../assets/latex/graphical_models_de527777dce5e0b8d981b548df9620f6c66785ca.png)
and
![\begin{equation*}
\begin{split}
\mu_{x_m \to f_s}(x_m) &= \prod_{l \in \text{ne}(x_m) \setminus \left\{ f_s \right\}} \Bigg[ \sum_{X_{ml}} F_l(x_m, X_{ml}) \Bigg] \\
&= \prod_{l \in \text{ne}(x_m) \setminus \left\{ f_s \right\}} \mu_{f_l \to x_m}(x_m)
\end{split}
\end{equation*}](../../assets/latex/graphical_models_3226a6e5accea75ba4dc8de769bf7b441a1333a0.png)
Once root node has received messages from all of its of its neighbors, the marginal can be evaluated by:
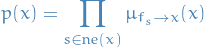
or, if one wants the marginal distribution
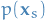 associated with the sets of variables belong to each of the factors:
associated with the sets of variables belong to each of the factors:

- If we started from a:
- directed graph: already correctly normalized
undirected graph: started with unknown normalization constant
 . From steps 1-4 we now have unnormalized marginal
. From steps 1-4 we now have unnormalized marginal  , which we can marginalize over a single one of these
, which we can marginalize over a single one of these  (holding all other variables constant), which then gives us the normalization constant:
(holding all other variables constant), which then gives us the normalization constant:
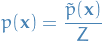
Could find marginals for every variable in the node in the graph by first passing messages from leaf to root, as in sum-product algorithm, and then when receiving all messages to the root, pass messages from the root back to the leaves.
Then we would have computed the messages along each of the links / edges in both directions, hence we could simply marginalize over these messages to obtain the wanted marginal.
Max-sum algorithm
Problem: find most probable state or sequence:

which will have the joint probability

- Summarized: barber2012
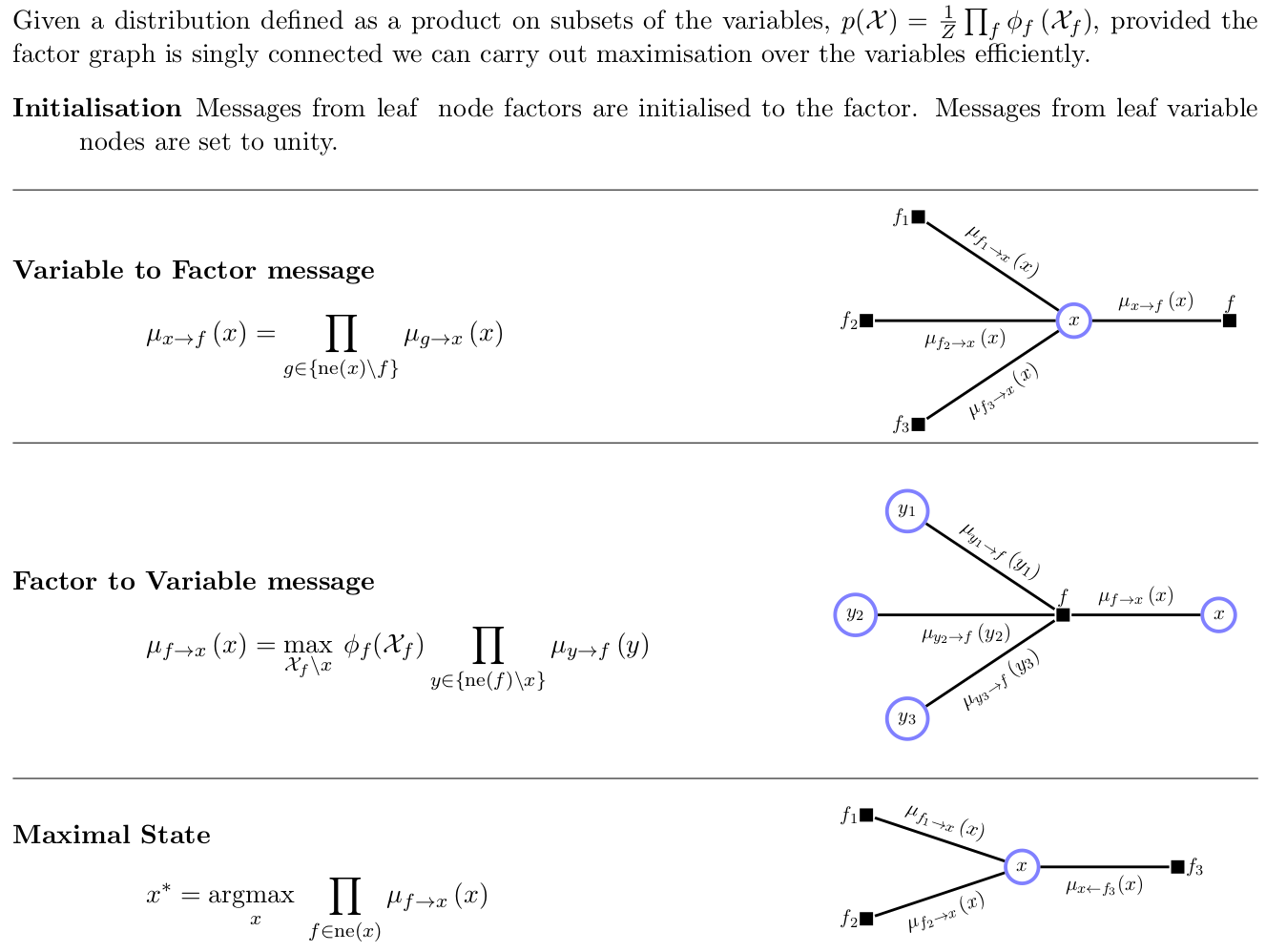
Figure 1: barber2012
Derivation
Will make use of

which holds if
 (always true for factors in graphical models!)
(always true for factors in graphical models!)
Work with
 instead (for numerical purposes), i.e.
instead (for numerical purposes), i.e.

where the distributive property is preserved since

hence we replace products with sums.
Causality
In setting any variable into a particular state we need to surgically remove all parental links of that variable.
This is called the do operator, and constrants observational ("see") inference  with a casual ("make" or "do") inference
with a casual ("make" or "do") inference  .
.
Formally, let all variables  be written in terms of the interventon variables
be written in terms of the interventon variables  and the non-intervention variables
and the non-intervention variables  .
.
For a Belief Network  , inferring the effect of setting variables
, inferring the effect of setting variables 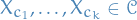 , in states
, in states  , is equivalent to standard evidential inference in the post intervention distribution:
, is equivalent to standard evidential inference in the post intervention distribution:
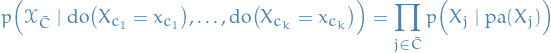
where any parental variable inclded in the intervention set is set to its intervention state. An alternative notation is
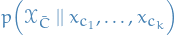
Intervention here refers to the "act of intervening", as in making some variable take on a particular state, i.e. we're interferring with the "total" state.
Bibliography
Bibliography
- [barber2012] Barber, Bayesian Reasoning and Machine Learning, Cambridge University Press (2012).