Expectation propagation

Table of Contents

Notation

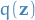
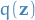  • $\text{KL}(p || q)$ denotes the Kullback-Leibler divergence, to be minimized wrt. $q(\mathbf{z})$

  • $q(\mathbf{z})$ is the approximate distribution, which is a member of the exponential family, i.e. can be written:

    \begin{equation*} q(\mathbf{z}) = h(\mathbf{z}) g(\boldsymbol{\eta}) \exp \Big( \boldsymbol{\eta}^T \mathbf{u}(\mathbf{z}) \Big) \end{equation*}
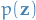  • $p(\mathbf{z})$ is a fixed distribution
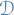  • $\mathcal{D}$ denotes the data
  • $\boldsymbol{\theta}$ denotes the parameters / hidden variables

Exponential family

The exponential family of distributions over $\mathbf{x}$, given parameters $\boldsymbol{\eta}$, is defined to be the set of distribtions of the form

\begin{equation*} p(\mathbf{x} \mid \boldsymbol{\eta}) = h(\mathbf{x}) g(\boldsymbol{\eta}) \exp \Big( \boldsymbol{\eta}^T \mathbf{u}(\mathbf{x}) \Big) \end{equation*}

where:

  • $\mathbf{x}$ may be discrete or continuous
  • $\mathbf{u}(\mathbf{x})$ is just some function of $\mathbf{x}$

MLE

If we wanted to estimate $\boldsymbol{\eta}$ in a density of the exponential family, we would simply take the derivative wrt $\boldsymbol{\eta}$ of the likelihood of the distribution and set to zero:

\begin{equation*} \nabla g(\boldsymbol{\eta}) \int h(\mathbf{x}) \exp \Big[ \boldsymbol{\eta}^T \mathbf{u}(\mathbf{x}) \Big] \ d \mathbf{x} + g (\boldsymbol{\eta}) \int h(\mathbf{x}) \exp \Big( \boldsymbol{\eta}^T \mathbf{u}(\mathbf{x}) \Big) \ d \mathbf{x} = 0 \end{equation*}

Rearranging, we get

\begin{equation*} - \frac{1}{g(\boldsymbol{\eta})} \nabla g(\boldsymbol{\eta}) = g(\boldsymbol{\eta}) \int h(\mathbf{x}) \exp \Big( \boldsymbol{\eta}^T \mathbf{u}(\mathbf{x}) \Big) = \mathbb{E} \big[ \mathbf{u}(\mathbf{x}) \big] \end{equation*}

which is just

\begin{equation*} - \nabla \ln g(\boldsymbol{\eta}) = \mathbb{E} \big[ \mathbf{u}(\mathbf{x}) \big] \end{equation*}

The covariance of $\mathbf{u}(\mathbf{x})$ can be expressed in terms of the second derivatives of $g(\boldsymbol{\eta})$, and similarily for higher order moments.

Thus, if we had set of i.i.d. data denoted by $\mathbf{X} = \left\{ \mathbf{x}_1, \dots, \mathbf{x}_n \right\}$, for which the likelihood function is given by

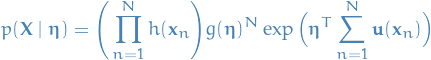
\begin{equation*} p(\mathbf{X} \mid \boldsymbol{\eta}) = \Bigg( \prod_{n = 1}^N h(\mathbf{x}_n \Bigg) g(\boldsymbol{\eta})^N \exp \Big( \boldsymbol{\eta}^T \sum_{n=1}^{N} \mathbf{u}(\mathbf{x}_n) \Big) \end{equation*}

which is minimized wrt. $\boldsymbol{\eta}$ when

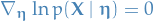
\begin{equation*} \nabla_{\boldsymbol{\eta}} \ln p(\mathbf{X} \mid \boldsymbol{\eta}) = 0 \end{equation*}

giving us the MLE estimator

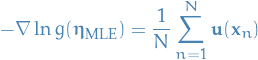
\begin{equation*} - \nabla \ln g (\boldsymbol{\eta}_{\text{MLE}}) = \frac{1}{N} \sum_{n=1}^{N} \mathbf{u}(\mathbf{x}_n) \end{equation*}

i.e. the MLE estimator depends on the data only through $\sum_n \mathbf{u}(\mathbf{x}_n)$, hence $\mathbf{u}(\mathbf{x})$ is a sufficient statistic.

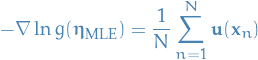
\begin{equation*} - \nabla \ln g (\boldsymbol{\eta}_{\text{MLE}}) = \frac{1}{N} \sum_{n=1}^{N} \mathbf{u}(\mathbf{x}_n) \end{equation*}

Minimizing KL-divergence between two exponential distributions

The KL divergence then becomes

\begin{equation*} \text{KL}(q || p) = - \ln g(\boldsymbol{\eta}) - \boldsymbol{\eta}^T \mathbb{E}_{p(\mathbf{z})} \big[ \mathbf{u}(\mathbf{z}) \big] + \text{const} \end{equation*}

where $\boldsymbol{\eta}$, $g(\cdot)$ and $\mathbf{u}(\cdot)$ define the approximation distribution $q$.

We're not making any assumptions regarding the underlying distribution of 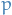$p$.

Which is minimized wrt. $\boldsymbol{\eta}$ by

\begin{equation*} - \nabla \ln g(\boldsymbol{\eta}) = \mathbb{E}_{p(\mathbf{z})} \big[ \mathbf{u}(\mathbf{z}) \big] \end{equation*}

From MLE estimator for exponential we then have

\begin{equation*} \mathbb{E}_{q(\mathbf{z})} \big[ \mathbf{u}(\mathbf{z}) \big] = \mathbb{E}_{p(\mathbf{z})} \big[ \mathbf{u}(\mathbf{z}) \big] \end{equation*}

hence, the optimum solution corresponds to matching the expected sufficient statistics!

Expectation propagation

  • Joint probability of data and parameters given by

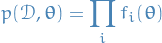
    \begin{equation*} p(\mathcal{D}, \boldsymbol{\theta}) = \prod_i f_i(\boldsymbol{\theta}) \end{equation*}

  • Want to evaluate

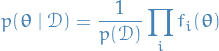
    \begin{equation*} p(\boldsymbol{\theta} \mid \mathcal{D}) = \frac{1}{p(\mathcal{D})} \prod_i f_i(\boldsymbol{\theta}) \end{equation*}

    and $p(\mathcal{D})$ for model comparison:

    \begin{equation*} p(\mathcal{D}) = \int \prod_i f_i(\boldsymbol{\theta}) \ d \boldsymbol{\theta} \end{equation*}

  • Expectation propagation is based on the approximation to the posterior distribution $p(\boldsymbol{\theta} \mid \mathcal{D})$ by $q(\boldsymbol{\theta})$

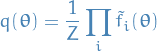
    \begin{equation*} q(\boldsymbol{\theta}) = \frac{1}{Z} \prod_i \tilde{f}_i (\boldsymbol{\theta}) \end{equation*}

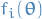    where $\tilde{f}_i(\boldsymbol{\theta})$ is an approximation to the factor $f_i(\boldsymbol{\theta})$ in the true posterior

  • To be tractable, need to constrain the approximators $\tilde{f}_i$ => assume to be exponential

  • Want to determine $\tilde{f}_i(\boldsymbol{\theta})$ by minimizing KL divergence between true and approx. posterior:

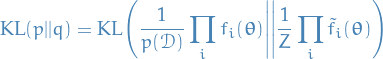
    \begin{equation*} \text{KL}(p || q) = \text{KL} \Bigg( \frac{1}{p(\mathcal{D})} \prod_i f_i(\boldsymbol{\theta}) \Bigg|\Bigg| \frac{1}{Z} \prod_i \tilde{f}_i(\boldsymbol{\theta}) \Bigg) \end{equation*}

One approach of doing this would be to minimize KL divergence between the pairs 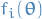$f_i(\boldsymbol{\theta})$ and $\tilde{f}_i(\boldsymbol{\theta})$ of factors.

It turns out that this no good; even though each of the factors are approximated individually, the product could still give a poor approximation.

(Also, if our assumptions are not true, i.e. true posterior is actually not of the exponential family, then clearly this approach would not be a good one.)

Expectation propagation optimizes each factor $\tilde{f}_i(\boldsymbol{\theta})$ in turn, given the "context" of all remaining factors.

Suppose we wish to update our estimate for $\tilde{f}_j(\boldsymbol{\theta})$, then we would like the following (assuming data was drawn from some exponential distribution):

\begin{equation*} q^{\text{new}}(\boldsymbol{\theta}) \propto \tilde{f}_j(\boldsymbol{\theta}) \prod_{i \ne j} \tilde{f}_i(\boldsymbol{\theta}) \approx f_j(\boldsymbol{\theta}) \prod_{i \ne j} \tilde{f}_j(\boldsymbol{\theta}) \end{equation*}

i.e. want to optimize for the j-th factor conditioned on our estimate for all the other factors. (Expectation maximization, anyone?)

This problem we can pose as minimizing the following KL divergence

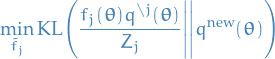
\begin{equation*} \min_{\tilde{f}_j} \text{KL} \Bigg( \frac{f_j(\boldsymbol{\theta}) q^{\backslash j}(\boldsymbol{\theta})}{Z_j} \Bigg|\Bigg| q^{\text{new}}(\boldsymbol{\theta}) \Bigg) \end{equation*}

where:

  • new approximate distribution:

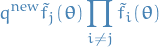
    \begin{equation*} q^{\text{new}} \prodto \tilde{f}_j(\boldsymbol{\theta}) \prod_{i \ne j} \tilde{f}_i(\boldsymbol{\theta}) \end{equation*}

  • the unnormalized distribution:

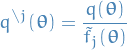
    \begin{equation*} q^{\backslash j}(\boldsymbol{\theta}) = \frac{q(\boldsymbol{\theta})}{\tilde{f}_j(\boldsymbol{\theta})} \end{equation*}

  • normalization with $\tilde{f}_j$ replaced by $f_j$:

    \begin{equation*} Z_j = \int f_j(\boldsymbol{\theta}) q^{\backslash j}(\boldsymbol{\theta}) \ d \boldsymbol{\theta} \end{equation*}

Which we already know comes down to having:

\begin{equation*} \mathbb{E}_{q(\mathbf{z})} \big[ \mathbf{u}(\mathbf{z}) \big] = \mathbb{E}_{p(\mathbf{z})} \big[ \mathbf{u}(\mathbf{z}) \big] \end{equation*}
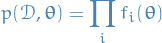
\begin{equation*} p(\mathcal{D}, \boldsymbol{\theta}) = \prod_i f_i(\boldsymbol{\theta}) \end{equation*}

and we wish to approximate the posterior distribution $p(\boldsymbol{\theta} \mid \mathcal{D})$ by a distribution of the form

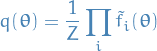
\begin{equation*} q(\boldsymbol{\theta}) = \frac{1}{Z} \prod_i \tilde{f}_i(\boldsymbol{\theta}) \end{equation*}

and the model evidence $p(\mathcal{D})$.

  1. Initialize all of the approximating factors $\tilde{f}_i(\boldsymbol{\theta})$

  2. Initialize the posterior approximation by setting

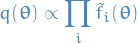
    \begin{equation*} q(\boldsymbol{\theta}) \propto \prod_i \tilde{f}_i(\boldsymbol{\theta}) \end{equation*}
  3. Until convergence:
    1. Choose a factor $\tilde{f}_j(\boldsymbol{\theta})$ to improve

    2. Remove $\tilde{f}_j(\boldsymbol{\theta})$ from posterior by division:

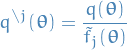
      \begin{equation*} q^{\backslash j}(\boldsymbol{\theta}) = \frac{q(\boldsymbol{\theta})}{\tilde{f}_j(\boldsymbol{\theta})} \end{equation*}

    3. Let $q^{\text{new}}(\boldsymbol{\theta})$ be such that

      \begin{equation*} \mathbb{E}_{q^{\backslash j} f_j(\boldsymbol{\theta}) / Z_j}(\boldsymbol{\theta})}\big[ \mathbf{u}(\boldsymbol{\theta}) \big] = \mathbb{E}_{q^{\text{new}}(\boldsymbol{\theta})} \big[ \mathbf{u}(\boldsymbol{\theta}) \big] \end{equation*}

      i.e. matching the sufficient statistics (moments) of $q^{\text{new}}(\boldsymbol{\theta})$ with those of $q^{\backslash j}(\boldsymbol{\theta}) f_j(\boldsymbol{\theta})$, including evaluating the normalization constant

      \begin{equation*} Z_j = \int q^{\backslash j}(\boldsymbol{\theta}) f_j(\boldsymbol{\theta}) \ d \boldsymbol{\theta} \end{equation*}

    4. Evaluate and store new factor

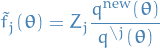
      \begin{equation*} \tilde{f}_j(\boldsymbol{\theta}) = Z_j \frac{q^{\text{new}}(\boldsymbol{\theta})}{q^{\backslash j}(\boldsymbol{\theta})} \end{equation*}

  4. Evaluate the approximation to the model evidence:

    \begin{equation*} p(\mathcal{D}) \approx \int \prod_i \tilde{f}_i(\boldsymbol{\theta}) \ d \boldsymbol{\theta} \end{equation*}

Notes

  • No guarantee that iterations will converge
    • Fixed-points guaranteed to exist when the approximations are in the exponential family
      • So at least then it converges, but to what? Dunno
      • Can also have multiple fixed-points
    • However, if iteratiors do converge; resulting solution will be a stationary point of a particular energy function (although each iteration is not guaranteed to actually decrease this energy function)
  • Does not make sense to apply EP to mixtures as the approximation tries to capture all of the modes of the posterior distribution

Moment matching / Assumed density filtering (ADF): a special case of EP

  • Initializes all $\tilde{f}_j(\boldsymbol{\theta})$ to unity and performs a single pass through the approx. factors, updating each of them once
  • Does not make use of batching
  • Highly dependent on order of data points, as $f_j(\boldsymbol{\theta})$ are only updated once