Expectation Maximization (EM)

Table of Contents

Summary

Expectation Maximization (EM) is an algorithm for obtaining the probability of some hidden random variable $\mathbf{Z}$ given some observations $\mathbf{X}$.

It is a two-step algorithm, which are repeated in order until convergence:

  1. Expectation-step: Choose some probability distribution $Q_i$,

    \begin{equation*} Q_i := P(z^{ (i) } | x^{ (i) }; \Theta) \end{equation*} 1

    which gives us a (tight) lower-bound for $l(\Theta)$ for the curren estimate of $\Theta$

  2. Maximization-step: optimize the

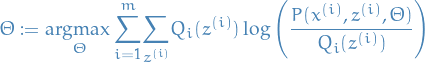    \begin{equation*} \Theta := \underset{\Theta}{\text{argmax }} \overset{m}{\underset{i=1}{\sum}} \underset{z^{(i)}}{\sum} Q_i (z^{ (i) }) \log \Bigg( \frac{P(x^{ (i) }, z^{ (i) }, \Theta)}{Q_i (z^{ (i) })} \Bigg) \end{equation*} 2

Or rather, following the notation of Wikipedia:

  1. Expectation step (E step): Calculate (or obtain an expression for) the expected value of the (complete) log likelihood function, with respect to the conditional distribution of $\mathbf {Z}$ given $\mathbf {X}$ under the current estimate of the parameters $\boldsymbol\theta^{(t)}$:

    \begin{equation*} Q(\boldsymbol\theta|\boldsymbol\theta^{(t)}) = \operatorname{E}_{\mathbf{Z}|\mathbf{X},\boldsymbol\theta^{(t)}}\left[ \log L (\boldsymbol\theta;\mathbf{X},\mathbf{Z}) \right] \end{equation*} 3

  2. Maximization step (M step): Find the parameter that maximizes this quantity:

    \begin{equation*} \boldsymbol\theta^{(t+1)} = \underset{\boldsymbol\theta}{\operatorname{arg\,max}} \ Q(\boldsymbol\theta|\boldsymbol\theta^{(t)}) \end{equation*} 4

Notation

  • $x^{ (i) }$ is the $i^{ \text{th} }$ observation
  • $z^{ (i) }$ is the rv. related to the $i^{ \text{th} }$
  • $\Theta$ is a set of parameters for our model, which we want to estimate
  • $l(\Theta)$ is the log-likelihood of the data given the estimated parameters $\Theta$
  • $\underset{z^{ (i) } \sim Q_i}{E} [ \dots ]$ means the expectation over the rv. $z^{ (i) }$ using the probability distribution $Q_i$

Goal

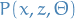
  • Have some model for $P(x, z, \Theta)$
  • Observe only $x$

  • Objective is then to maximize:

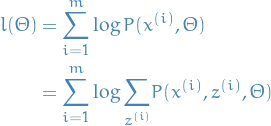    \begin{equation*} \begin{split} l(\Theta) &= \overset{m}{\underset{i = 1}{\sum}} \log P(x^{(i)}, \Theta) \\ &= \overset{m}{\underset{i=1}{\sum}} \log \underset{z^{(i)}}{\sum} P(x^{(i)}, z^{(i)}, \Theta) \end{split} \end{equation*} 5

    i.e. maximize the log-likelihood over the parameters $\Theta$ by marginalizing over the rvs. $z^{ (i) }$.

Idea

The idea behind the EM algorithm is to at each step construct a lower-bound for the log-likelihood using our estimate for $\Theta$ from the previous step. In this sense, the EM algorithm is a type of inference known as variational inference.

The reason for doing this is that we can often find a closed-form optimal value for 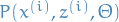$P(x^{(i)}, z^{(i)}, \Theta)$, which is not likely to be the case if we simply tried to take the derivative of $P(x^{(i)}, \Theta)$ set to zero and try to solve.

Finding the optimal parameters for the M-step is just to take the derivative of the M-step, set to zero and solve. It turns out that this is more often easier than directly doing the same for $l(\Theta)$.

Viewing it in the form coordinate descent

If we let

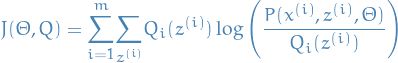\begin{equation*} J(\Theta, Q) = \overset{m}{\underset{i=1}{\sum}} \underset{z^{(i)}}{\sum} Q_i (z^{ (i) }) \log \Bigg( \frac{P(x^{ (i) }, z^{ (i) }, \Theta)}{Q_i (z^{ (i) })} \Bigg) \end{equation*} 6

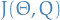then we know from Jensen's inequality that $l(\Theta) \geq J(\Theta, Q)$, and so increasing $J(\Theta, Q)$ at each step also monotonically increases the log-likelihood $l(\Theta)$. It can be shown that this is then equivalent to using coordinate descent on $J$.

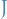Derivation

If we take our objective defined above, we and simply multiply by 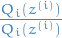$\frac{Q_i (z^{(i)})}{Q_i (z^{(i)})}$, we get:

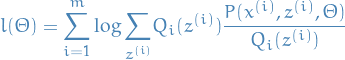\begin{equation*} l(\Theta) = \overset{m}{\underset{i=1}{\sum}} \log \underset{z^{(i)}}{\sum} Q_i (z^{ (i) }) \frac{P(x^{ (i) }, z^{ (i) }, \Theta)}{Q_i (z^{ (i) })} \end{equation*} 7

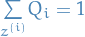Where we choose $Q_i$ to be s.t. $Q_i (z^{ (i) }) \geq 0$ and $\underset{z^{ (i) }}{\sum} Q_i = 1$, i.e. $Q_i$ is a probability distribution.

We then observe that the last sum (within the $\log$) is actually the following expectation:

\begin{equation*} \underset{z^{(i)}}{\sum} Q_i (z^{ (i) }) \frac{P(x^{ (i) }, z^{ (i) }, \Theta)}{Q_i (z^{ (i) })} = \underset{z^{ (i) } \sim Q_i}{E} \Bigg[ \frac{P(x^{ (i) }, z^{ (i) }, \Theta)}{Q_i (z^{ (i) })} \Bigg] \end{equation*} 8

Now using Jensen's inquality for a concave (because $\log (a)$ is concave) function $f$, which tells us $f(E[X]) \geq E[f(X)]$:

\begin{equation*} \log \Bigg( \underset{z^{ (i) } \sim Q_i}{E} \Bigg[ \frac{P(x^{ (i) }, z^{ (i) }, \Theta)}{Q_i (z^{ (i) })} \Bigg] \Bigg) \geq \underset{z^{ (i) } \sim Q_i}{E} \Bigg[ \log\Bigg( \frac{P(x^{ (i) }, z^{ (i) }, \Theta)}{Q_i (z^{ (i) })} \Bigg) \Bigg] \end{equation*} 9

Thus, we have constructed a lower-bound on the log-likelihood:

\begin{equation*} l(\Theta) \geq \overset{m}{\underset{i=1}{\sum}} \underset{z^{ (i) } \sim Q_i}{E} \Bigg[ \log\Bigg( \frac{P(x^{ (i) }, z^{ (i) }, \Theta)}{Q_i (z^{ (i) })} \Bigg) \Bigg] \end{equation}x Now what we want is for this inequality to be /tight/, i.e. that we have /equality/, so that we ensure we're actually improving our estimate by each step. Therefore we want to choose $Q_i$ s.t. \begin{equation} \frac{P(x^{ (i) }, z^{ (i) }, \Theta)}{Q_i (z^{ (i) })} = \text{constant}, \quad \forall z^{ (i) } \end{equation*} 10

Why? This would imply that the expectation above would also be constant. And since $f(c) = E[f(c)]$ is true for any constant $c$, the inequality would be tight, i.e. be an equality, as wanted!

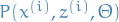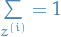It's also equivalent of saying that we want $Q_i$ to be proportional to $P(x^{ (i) }, z^{ (i) }, \Theta)$. Combining this with the fact that we want $Q_i$ to be a probability distribution, so we need to satisfy the proportionality and $\underset{z^{ (i) }}{\sum} = 1$. Then it turns out (makes sense, since we need it to sum to 1 and be prop to $P$) that we want:

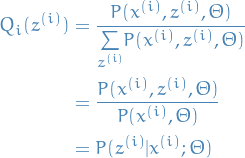\begin{equation*} \begin{split} Q_i(z^{ (i) }) &= \frac{P(x^{ (i) }, z^{ (i) }, \Theta)}{\underset{z^{ (i) }}{\sum} P(x^{ (i) }, z^{ (i) }, \Theta)} \\ &= \frac{P(x^{ (i) }, z^{ (i) }, \Theta)}{P(x^{ (i) }, \Theta)} \\ &= P(z^{ (i) } | x^{ (i) }; \Theta) \end{split} \end{equation*} 11

Which gives us the E-step of the EM-algorithm:

\begin{equation*} Q_i := P(z^{ (i) } | x^{ (i) }; \Theta) \end{equation*} 12

Giving us a (tight) lower-bound for $l(\Theta)$ for the current estimate of $\Theta$.

The M-step is then to optimize that lower-bound wrt. $\Theta$:

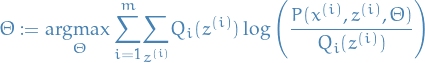\begin{equation*} \Theta := \underset{\Theta}{\text{argmax }} \overset{m}{\underset{i=1}{\sum}} \underset{z^{(i)}}{\sum} Q_i (z^{ (i) }) \log \Bigg( \frac{P(x^{ (i) }, z^{ (i) }, \Theta)}{Q_i (z^{ (i) })} \Bigg) \end{equation*} 13

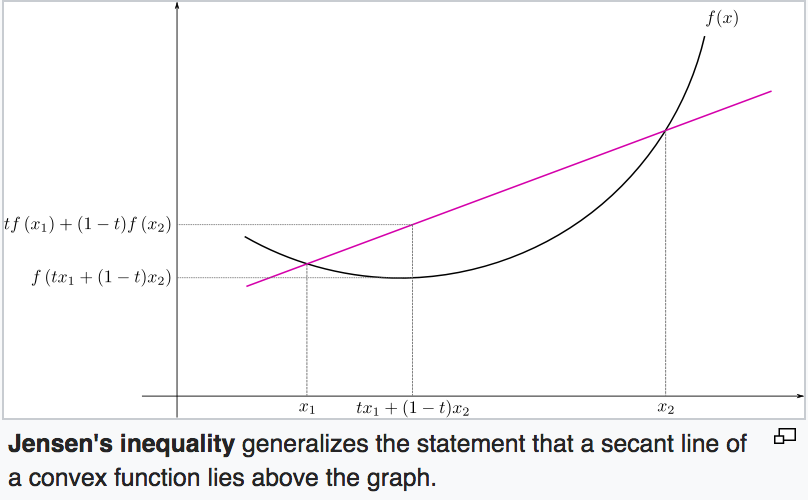
Appendix A: Jensen's inquality

If

  • $f$ is a convex function.
  • $X$ is a rv.

Then $f(E[X]) \leq E[f(x)]$.

Further, if $f''(x) > 0$ ($f$ is strictly convex), then $E[(f(X)] = f(E[X]) \iff X = E[X]$ "with probability 1".

If we instead have:

  • $f$ is a concave function

Then $f(E[X]) \geq E[f(X)]$. This is the one we need for the derivation of EM-algorithm.

To get a visual intuition, here is a image from Wikipedia: jensens_inequality.png