Clustering algorithms
Table of Contents
Notation
 is the
is the  observation
observation is the dimension of the data, i.e.
is the dimension of the data, i.e. 
K-means clustering
Summary
- Guarantees local minima converges
- No guarantee for global minima
Notation
 is the mean of the
is the mean of the  cluster
cluster
Idea
K-means clustering is performing using two steps:
Randomly initialize
 cluster centroids with means
cluster centroids with means
 1
1
Repeat until convergence:
- Set
 , i.e. assign the
, i.e. assign the  data
to the cluster for which it is closest to the mean.
data
to the cluster for which it is closest to the mean. - Update mean of cluster as follows:
 μj = { {} 1 \{c(i) = j \} x(i)}
{{} 1 \{c(i) = j\} }
μj = { {} 1 \{c(i) = j \} x(i)}
{{} 1 \{c(i) = j\} }
- Set
Convergence here means until the assignments to the different clusters do not change.
Gaussian mixture models
Summary
Notation
 is the latent / unobserverd / hidden random variable which we want to estimate
is the latent / unobserverd / hidden random variable which we want to estimate is the assigned cluster for the
is the assigned cluster for the  observation
observation 
 represents the probability of the
represents the probability of the  "cluster" assignment
"cluster" assignment
Idea
We have a latent random variable  and
and 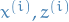 have a joint distribution:
have a joint distribution:
 2
2
The model is as follows:
 where
where 

Note that this model is identical to Gaussian Discriminant Analysis, except the fact that we have replaced our labeled outputs
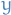 by latent
variable
by latent
variable  .
.
Optimization
Special case of EM
See this for more on Expectation Maximization (EM).
Repeat until convergence:
(E-step) Guess values of
 's and compute:
's and compute:
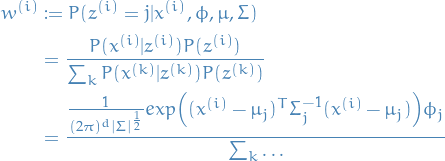 3
3
Where the
 means that we sum over the same expression as
in the numerator for every
means that we sum over the same expression as
in the numerator for every  , and the numerator is simply the Gaussian PDF
multiplied by the probability of
, and the numerator is simply the Gaussian PDF
multiplied by the probability of  .
.
- (M-step) Compute for each cluster
 :
:
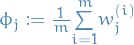 , i.e. take average of weights computed above
, i.e. take average of weights computed above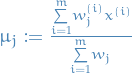 , i.e. weighted average for the ith observation
, i.e. weighted average for the ith observation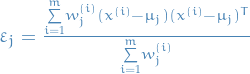 , i.e. the variance using the previously computed weights
, i.e. the variance using the previously computed weights
Parallels to Gaussian Discriminant Analysis
In GDA we have:
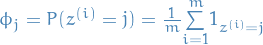
But in our case (GMM) we do not know which cluster the observation
belongs to, so instead we use the "soft-weights" 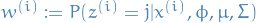 and so get
and so get 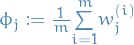 .
.
Mean-shift
- Non-parametric feature-space analysis technique for locating a maxima of a density function, a so-called mode-seeking algorithm
Mean shift is an iterative method for locating the maxima - the modes - of density function given discrete data sampled from that function.
- Choose a kernel function
 , which determines the weights of the nearby points for re-estimation of the mean.
, which determines the weights of the nearby points for re-estimation of the mean. The weighted mean of the density in the window determined by
 is
is
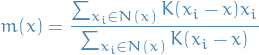
where
 is the neighborhood of
is the neighborhood of  , a set of points for which
, a set of points for which 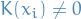 .
.
- Set

- Repeate 2-3 until
 converges
converges
The procedure gets it's name from the difference 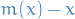 , which is called the mean shift.
, which is called the mean shift.
A rigid proof for convergence of the algorithm using a general kernel in a high dimensional space is still not known.
Convergence has been shown for one-dimension with differentiable, convex, and strictly increasing profile function.
Convergence in higher dimensions with a finite number of the stationary points (or isolated) has been proven, however, sufficient conditions for a general kernel to have a finite (or isolated) stationary points have not been provided.