Symmetries of Particles and Fields
Table of Contents
 is the symmetries of electrodynamics
is the symmetries of electrodynamics is the symmetries of the weak interactions
is the symmetries of the weak interactions is the symmetries of the color (quarks)
is the symmetries of the color (quarks)
Metric tensor
 has real eigenvalues
has real eigenvalues  :
:
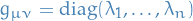
Rescale sucht that
 keeping
keeping  fixed. Rescaling follows
fixed. Rescaling follows
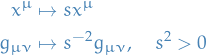
which we can do separately for each
 , hence
, hence
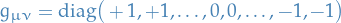
which we call the canonical basis.
Example: space time
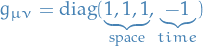
such that
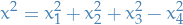
Usually, we use the opposite signature metric, using  and $x4 = x0:
and $x4 = x0:

which gives
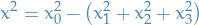
Raising and lowering indices using the metric tensor
 if and only if
if and only if  is invertible.
is invertible.
Can use metric to raise and lower indices

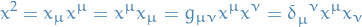
Can raise indices of metric
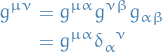
were we've contracted over  . Then
. Then

which implies  is the /inverse of
is the /inverse of  .
.
Same with Levi-Civita symbols

and derivatives wrt. $xμ
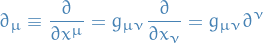
If metric is definite
If metris is definite, the we can choose basis such that 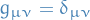 , i.e. can ignore distinction between upper and lower indices!
, i.e. can ignore distinction between upper and lower indices!
Matrix groups
Lorentz group
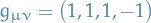
is called  which has
which has  .
.
1D groups
All 1D Lie groups are such that the parameter  can be chosen such that
can be chosen such that

Furthermore, all 1D Lie groups are Abelian.
 and
and  are isomorphic.
are isomorphic.
Let  be a
be a  dimensional compact Abelian Lie group. Then
dimensional compact Abelian Lie group. Then
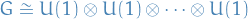
If  is compact, then for every representation there exists an equivalent unitary representation.
is compact, then for every representation there exists an equivalent unitary representation.
Lie algebras
Generators
Consider group 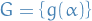 where we choose
where we choose 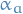 with
with ![$a \in [1, \dim G]$](../../assets/latex/symmetries_of_particles_and_fields_0dc91a7de12fd0d443d5ca7cfc3794cf84d34532.png) such that
such that
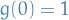
Taylors thm expand  about
about 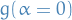 , so we can write
, so we can write
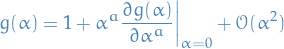
for "small"  .
.
Define
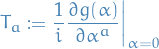
Matrices  are the generators of the group.
are the generators of the group.
The  is put in to make
is put in to make  hermitian (in a unitary representation).
hermitian (in a unitary representation).
Examples
Example: 
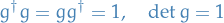
which implies

Thus, the generators are hermitian and traceless.
Example: 
We generally choose Pauli matrices as generators:
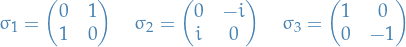
Example: 
Generators are Gell-Mann
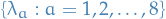
Example: 
- Don't have constraint
 .
. - Generators of
 ,
,  are also the part a subset of the generators of
are also the part a subset of the generators of  , and "including the trace" we have
, and "including the trace" we have  as the generators for
as the generators for 
Example: 
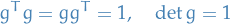
for  ,
, 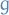 is real, where we generally omit the
is real, where we generally omit the  in the def. of generators.
in the def. of generators.
Taking Taylor expansion, as for  , we have
, we have

i.e.  are anti-symmetric.
are anti-symmetric.
Example:  and
and 
For  , generally choose:
, generally choose:
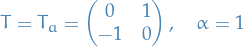
For  , generally choose
, generally choose
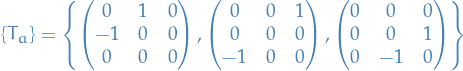
Additional constraint  is automatically satisfied (why?).
is automatically satisfied (why?).
Commutations
Consider  with
with  .
.
Expanding each of these using their Taylor expansion up to and including 2nd order terms, then take the commutation relation between  and
and  , the expansion of
, the expansion of 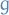 and
and  , respectively, we have
, respectively, we have
For this to be true  we must have
we must have

for some numbers 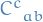 .
.
Which implies
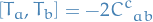
where 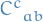 are called the structure constants.
are called the structure constants.
Exponentiation
Consider 1D subgroup  ,
,  labeled by the single parameter
labeled by the single parameter  .
.
Chose  such that
such that

Diff. wrt. 

and set  , which gives us a differential equation for all
, which gives us a differential equation for all  :
:
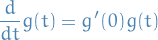
which has the solution
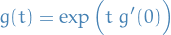
Or, if you consider this in the familiar notation used in Diff. Geom. for the exponential map, we can write this as

where  , s.t.
, s.t.

where  , i.e. maps from the Lie algebra to the Lie group.
, i.e. maps from the Lie algebra to the Lie group.
Going back to the earier notation of  , we can write
, we can write
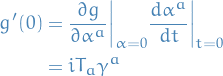
where
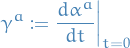
which implies

Adjoint representation
Can define an adjoint representation:

then

Examples
 and
and 
 take generators
take generators 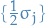 , with
, with
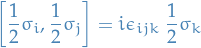
and so the structure constants are
 .
.
Consider

Then
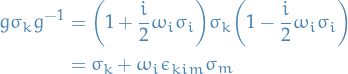
So if we write
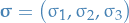 , then we can write
, then we can write

which is just rotation in
 !
!
Therefore the adjoint representation of
 is the defining or fundamental representation of
is the defining or fundamental representation of  . hence
. hence

for elements "close to the identity".
In general, the adjoint representation is not the fundamental representation of some other group…
Killing form
The Killing form

real symmetric  matrix.
matrix.
Usually we'll choose diagonal basis such that

Examples

So we rescale generators such that
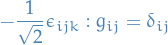
Application of killing form
- Can use Killing form to lower and raise indices
E.g. kan define structure consts with all lower indices

This is an invariant tensor → can be written as a product of generators
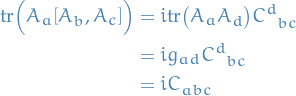
Invariant Tensors
Let  be a Lie group.
be a Lie group.
An invariant tensor

is a tensor that remains invariant under the actions of group  , i.e.
, i.e.
