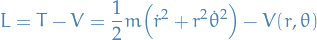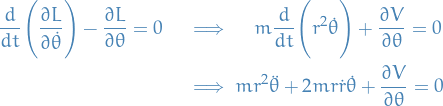Lagrangian Dynamics

Table of Contents

Notation

  • $\mathbf{r}$ position vector of particle of mass $m$
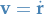  • $\mathbf{v} = \dot{\mathbf{r}}$ is velocity
  • $\mathbf{p} = m \mathbf{v}$ is linear momentum
  • $T$ is kinetic energy
  • $\mathbf{e}_\phi$ is the unit vector perpendicular to $\mathbf{e}_r$ (the unit position vector)

Stuff

Equations / Theorems

Galilean Transformation

Transforms from one inertial frame to another moving at constant velocity $V$ relative to it

\begin{equation*} \mathbf{r} = \mathbf{r}' + \mathbf{V} t + \mathbf{b}, \quad \dot{\mathbf{V}} = \mathbf{0}, \dot{\mathbf{b}} = 0 \end{equation*}

Then,

\begin{equation*} \mathbf{v} = \mathbf{v}' + \mathbf{V} \end{equation*}
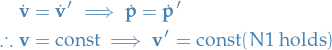
\begin{equation*} \begin{split} \dot{\mathbf{v}} &= \dot{\mathbf{v}}' \implies \dot{\mathbf{p}} = \dot{\mathbf{p}}' \\ \therefore \mathbf{v} &= \text{const} \implies \mathbf{v}' = \text{const} (N1 \text{ holds}) \\ \end{split} \end{equation*}

Conservation laws

Linear momentum

Angular momentum

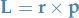
\begin{equation*} \mathbf{L} = \mathbf{r} \times \mathbf{p} \end{equation*}
Proof
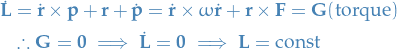
\begin{equation*} \begin{split} \dot{\mathbf{L}} &= \dot{\mathbf{r}} \times \mathbf{p} + \mathbf{r} + \dot{\mathbf{p}} = \dot{\mathbf{r}} \times \omega \dot{\mathbf{r}} + \mathbf{r} \times \mathbf{F} = \mathbf{G} (\text{torque}) \\ & \therefore \mathbf{G} = \mathbf{0} \implies \dot{\mathbf{L}} = \mathbf{0} \implies \mathbf{L} = \text{const} \end{split} \end{equation*}

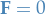
Remember, in this case we have $\mathbf{r} || \mathbf{F}$ and thus $× $\mathbf{F} = 0$

Lagrange's equations

Equations of motion in terms of generalised coordinates.

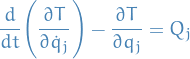
\begin{equation*} \frac{d}{dt} \Bigg( \frac{\partial T}{\partial \dot{q}_j}\Bigg) - \frac{\partial T}{\partial q_j} = Q_j \end{equation*}
  • equivalent to Newton's laws
  • constraint equation have been eliminated
  • constraint forces do not appear - they don't contribute to $\{Q_j\}$

Remember that the generalized forces $\{Q_j\}$ are simply the forces projected onto the generalized coordinates $\{q_j\}$.

Derivation

We restrict our attention to functions of the form 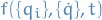$f(\{q_i\}, \{\dot{q}\}, t)$, where $\{q_i\}$ denotes the generalised coordinates.

We assume Newton's Laws to be true in this derivation.

Since 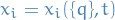$x_i = x_i(\{q\}, t)$ we can apply the "cancellation of dots" which just says that for the case where $f$ is not a function of $\{\dot{q}_i\}$, then we have

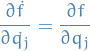
\begin{equation*} \frac{\partial \dot{f}}{\partial \dot{q_j}} = \frac{\partial f}{\partial q_j} \end{equation*}

thus,

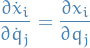
\begin{equation*} \frac{\partial \dot{x}_i}{\partial \dot{q}_j} = \frac{\partial x_i}{\partial q_j} \end{equation*}
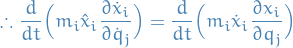
\begin{equation*} \therefore \frac{d}{dt} \Big( m_i \hat{x}_i \frac{\partial \dot{x}_i}{\partial \dot{q}_j} \Big) = \frac{d}{dt} \Big( m_i \dot{x}_i \frac{\partial x_i}{\partial q_j} \Big) \end{equation*}

Further,

\begin{equation*} \begin{align} \frac{d}{dt} \Bigg[ \frac{\partial}{\partial \dot{q}_j} \Big(\frac{1}{2} m_i \dot{x}_i^2 \Big) \Bigg] &= \frac{d}{dt} \big( m_i \dot{x}_i \big) \frac{\partial x_i}{\partial q_j} + m_i \dot{x}_i \frac{d}{dt} \Big( \frac{\partial x_i}{\partial q_j} \Big) \\ &= m_i \ddot{x}_i \frac{\partial x_i}{\partial q_j} + m_i \dot{x}_i \frac{\partial}{\partial q_j} \dot{x}_i \\ &= F_i \frac{\partial x_i}{\partial q_j} + \frac{\partial}{\partial q_j} \Big( \frac{1}{2} m_i \dot{x}_i^2 \Big) \quad & \text{by Newtons 2nd law} \end{align} \end{equation*}

Summing over $i$

\begin{equation*} \frac{d}{dt} \Bigg[ \frac{\partial}{\partial \dot{q}_j} \Big( \sum_i \frac{1}{2} m_i \dot{x}_i^2 \Big) \Bigg] \end{equation*}

we see that it's just the kinetic energy $T$ as a function of the generalised coordinates, velocities and time.

Thus,

\begin{equation*} \frac{d}{dt} \Bigg[ \frac{\partial}{\partial \dot{q}_j} \Big( \sum_i \frac{1}{2} m_i \dot{x}_i^2 \Big) \Bigg] = \sum_i F_i \frac{\partial x_i}{\partial q_j} + \frac{\partial}{\partial q_j} \Big( \sum_i \frac{1}{2} m_i \dot{x}_i^2 \Big) \end{equation*}

where the first term is just 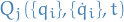$Q_j(\{q_i\}, \{\dot{q}_i\}, t)$.

Since the constraint forces do now work, the sum over all constraint forces is zero.

Therefore we end up with Lagrange Equations

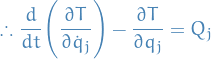
\begin{equation*} \therefore \frac{d}{dt} \Bigg( \frac{\partial T}{\partial \dot{q}_j}\Bigg) - \frac{\partial T}{\partial q_j} = Q_j \end{equation*}

Using conservative forces

If the forces are conservative there exists a potential energy function such that

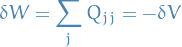
\begin{equation*} \delta W = \sum_j Q_j \deltaq_j = - \delta V \end{equation*}

Assume $V = V(\{qj\}, t) then

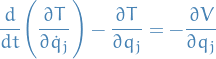
\begin{equation*} \frac{d}{dt} \Bigg( \frac{\partial T}{\partial \dot{q}_j} \Bigg) - \frac{\partial T}{\partial q_j} = - \frac{\partial V}{\partial q_j} \end{equation*}

Since $\frac{\partial V}{\partial \dot{q}_j} = 0$, we may write

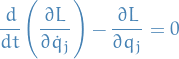
\begin{equation*} \frac{d}{dt} \Bigg( \frac{\partial L}{\partial \dot{q}_j} \Bigg) - \frac{\partial L}{\partial q_j} = 0 \end{equation*}

where $L(\{q_j\}, \{\dot{q}_j\}, t) = T(\{q_j\}, \{\dot{q}_j\}, t) - V(\{q_j\}, t)$

This is for holonomic constraints.

This applies to systems which also does not conserve their energy, unlike the usual

\begin{equation*} T + V \end{equation*}

which is only valid for systems which conserve energy.

Examples
  • Single particle in Cartesian Coordinate

    We have

    \begin{equation*} L = T - V = \frac{1}{2} \sum_{i = 1}^{3} m \dot{x_i}^2 - V(\{x_i\}) \end{equation*}

    Substituting into Lagrange's equation for conservative forces

    \begin{equation*} \frac{d}{dt} \Bigg( \frac{\partial L}{\partial \dot{q}_i} \Bigg) - \frac{\partial L}{\partial x_i} = 0 \quad \implies \quad m \ddot{x}_i + \frac{\partial V}{\partial x_i} = 0 \end{equation*}
  • Single particle in polar coordinates
    \begin{equation*} T = \frac{1}{2} m \Big[ \dot{r}^2 + (r \dot{\theta})^2 \Big] \end{equation*}
    \begin{equation*} L = T - V = \frac{1}{2} m \Big( \dot{r}^2 + r^2 \dot{\theta}^2 \Big) - V(r, \theta) \end{equation*}

    Substituing into Lagrange's equations wrt. $r_i$

    \begin{equation*} \frac{d}{dt} \Bigg( \frac{\partial L}{\partial \dot{r}_i} \Bigg) - \frac{\partial L}{\partial x_i} = 0 \quad \implies m \ddot{r} - m r \dot{\theta}^2 + \frac{\partial V}{\partial r} = 0 \end{equation*}

    and wrt. $\theta$

    \begin{equation*} \begin{split} \frac{d}{dt} \Bigg( \frac{\partial L}{\partial \dot{\theta}} \Bigg) - \frac{\partial L}{\partial \theta} = 0 \quad & \implies \quad m \frac{d}{dt} \Bigg( r^2 \dot{\theta} \Bigg) + \frac{\partial V}{\partial \theta} = 0 \\ & \implies mr^2 \ddot{\theta} + 2mr \dot{r} \dot{\theta} + \frac{\partial V}{\partial \theta} = 0 \end{split} \end{equation*}

Definitions

Intertial frame

A frame in which Newtons 1st and 2nd laws hold.

Newtons Laws

Newtons 3rd law

Weak
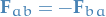
\begin{equation*} \mathbf{F}_{ab} = - \mathbf{F}_{ba} \end{equation*}

for two objects $a$ and $b$ acting on each other.

Strong

Weak assumption AND $\mathbf{F}_{ab}$ acts along $\mathbf{r}_a - \mathbf{r}_b$

Effect potential

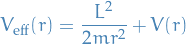
\begin{equation*} V_{\text{eff}} (r) = \frac{L^2}{2 m r^2} + V(r) \end{equation*}

due to

\begin{equation*} E = T + V = \frac{1}{2} m (\dot{r}^2 + r^2 \dot{\phi}^2 ) + V(r) \end{equation*}

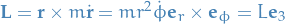where $\mathbf{L} = \mathbf{r} \times m \dot{\mathbf{r}} = m r^2 \dot{\phi} \mathbf{e}_r \times \mathbf{e}_\phi = L \mathbf{e}_3$ gives us

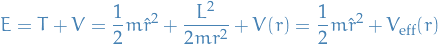
\begin{equation*} E = T + V = \frac{1}{2} m \hat{r}^2 + \frac{L^2}{2m r^2} + V(r) = \frac{1}{2} m \hat{r}^2 + V_\text{eff}(r) \end{equation*}

Constraint force

Constraint forces do no work in any small instantaneous displacement of the system consistent with the constraints themselves.

Does not mea that the constraint forces can do no work during the actual motion of the system, e.g. a particle constrained to lie on a surface which is itself moving: there may then be a component of the actual particle velocity in the direction of the constraint force, so that work is done.

Circular orbits

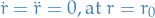
\begin{equation*} \dot{r} = \ddot{r} = 0, \text{at} \ r = r_0 \end{equation*}
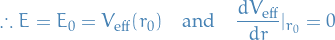
\begin{equation*} \therefore E = E_0 = V_\text{eff}(r_0) \quad \text{and} \quad \frac{d V_\text{eff}}{dr} |_{r_0} = 0 \end{equation*}

Holonomic constraints

Example

\begin{equation*} f(\mathbf{r}_a, \mathbf{r}_b, \dots, \mathbf{r}_N; \ t) = 0 \end{equation*}

i.e. it's a algebraic equation between the coordinates, not a differentiable relation and not an inequality.

Generalised coordinates

Consider a system with 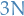$3N$ coordinates, i.e. 3D with $N$ particles each with coordinates, and let these coordinates be denoted by $xi,$ where $i=1, \dots, 3N$.

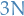That is, we're just "flattening" the $N \times 3$ matrix to a $3N$ vector.

If $\exists M$ holonomic constraints, not all $x_i$ are independent, and $\exists a$ set of independent variables

\begin{equation*} q_i = q_i (x_1, \dots, x_{3N}, t), \quad i=1, \dots, 3N - M \end{equation*}

We might have dependence between the $x_i$ due to the constraints being imposed, and thus representing the coordinates in the above way is just "removing" the dependence between the $x_i$.

Hence, we end up with a basis of 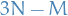$3N - M$ dimensions.

Our aim is to derive 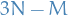$3N-M$ 2nd order differential eq. for the set of generalised coordinates $\{q_i\}$.

Transformation from $\{x\}$ to $\{q\}$ is invertible using constraint eq., that is:

\begin{equation*} x_i = x_i \Big( \{q_j\}, t) \end{equation*}

$\{x_i\}$ cannot be varied independently without violating the constraints, whereas we can vary $\{q_i\}$ while still satisfying the constraints.

Generalised velocities

If $\{q_i\}$ denotes the generalised coordinates, then $\{\dot{q}_i\}$ represents the generalised velocities.

Generalised forces

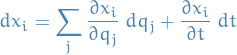
\begin{equation*} d x_i = \sum_j \frac{\partial x_i}{\partial q_j} \ dq_j + \frac{\partial x_i}{\partial t} \ dt \end{equation*}

Here 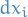$dx_i$ may have a component in the direction of a constraint force, due to motion, and so the constraint force may do work, e.q. a body on a surface is utself moving.

"Instantaneous", i.e. 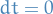$dt = 0$

Then a small change consistent with constraints

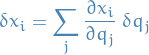
\begin{equation*} \delta x_i = \sum_j \frac{\partial x_i}{\partial q_j} \ \delta q_j \end{equation*}

In a virtual displacement the work done is

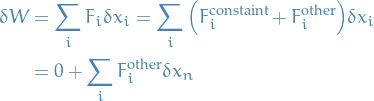
\begin{equation*} \begin{align} \delta W &= \sum_i F_i \delta x_i = \sum_i \Big( F_i^\text{constaint} + F_i^\text{other} \Big) \delta x_i \\ &= 0 + \sum_i F_i^\text{other} \delta x_n \end{align} \end{equation*}

since constraint forces do no work.

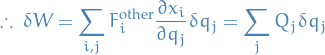
\begin{equation*} \therefore \ \delta W = \sum_{i, j} F_i^\text{other} \frac{\partial x_i}{\partial q_j} \delta q_j = \sum_j Q_j \delta q_j \end{equation*}

where

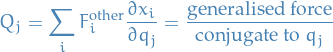
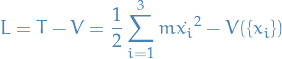
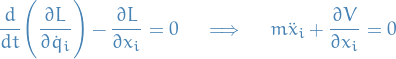
\begin{equation*} Q_j = \sum_i F_i^\text{other} \frac{\partial x_i}{\partial q_j} = \frac{\text{generalised force}}{\text{conjugate to } q_j} \end{equation*}

Problems

Stuff