Quantum Mechanics
Table of Contents
2. A First Approach to Classical Mechanics
2.5 Poisson Brackets and Hamiltonian Mechanics
Let  and
and 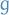 be two smooth functions on
be two smooth functions on 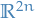 , where an element of
, where an element of 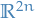 is thought of as a pair
is thought of as a pair  , with
, with
 representing position of a particle
representing position of a particle
 representing the momentum of a particle
representing the momentum of a particle
Then the Poisson bracket of  and
and 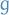 , denoted
, denoted 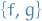 is the function on
is the function on 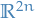 given by
given by
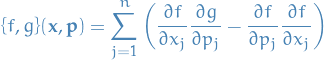
For all smooth functions  ,
, 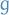 and
and  on
on 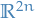 we have the following:
we have the following:
 for all
for all 
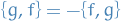
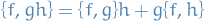
Jacobi identity:

The position and momentum functions satisfy the following Poisson bracket relations:
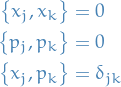
If a particle in 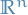 has the usual sort of energy function (kinetic energy plus potential energy), we have
has the usual sort of energy function (kinetic energy plus potential energy), we have
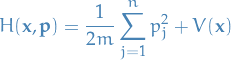
Wit the Hamiltonian, and as usual, having  , we can write Netwon's laws as:
, we can write Netwon's laws as:
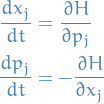
These equations we refer to has Hamilton's equations.
If  is a solution of the Hamilton's equation, then for any function
is a solution of the Hamilton's equation, then for any function  on
on 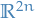 , we have
, we have
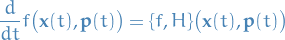
Call a smooth function  on
on  a conserved quantity if
a conserved quantity if  is independent of
is independent of  for each solution
for each solution  of Hamilton's equations.
of Hamilton's equations.
Then  is a conserved quantity if and only if
is a conserved quantity if and only if

In particular, the Hamiltonian  is a conserved quantity.
is a conserved quantity.
Solving Hamilton's equatons on  gives rise to a flow on
gives rise to a flow on  , that is, a family
, that is, a family  of diffeomorphisms of
of diffeomorphisms of 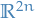 , where
, where  is equal to the solution at time
is equal to the solution at time  of Hamilton's equations with initial conditions
of Hamilton's equations with initial conditions  .
.
Since it is possible (depending on the choice of potential function  ) that a particle can escape to infinity in finite time, the maps
) that a particle can escape to infinity in finite time, the maps  are not necessarily defined on all of
are not necessarily defined on all of 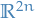 , but only on some subset therof.
, but only on some subset therof.
If  is defined on all of
is defined on all of 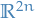 we say it's complete.
we say it's complete.
The flow associated with Hamilton's equations, for an arbitrary Hamitonian function  , preserves the (2n)-dimensional volume measure
, preserves the (2n)-dimensional volume measure
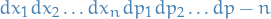
What this means, more precisely, is that if a measurable set  is contained in the domain of
is contained in the domain of  for some
for some  , then the volume of
, then the volume of  is equal to the volume of
is equal to the volume of  .
.