Optimization

Table of Contents

THE resource

jain17_non_convex_optim_machin_learn

Notation

  • Support of a vector $\mathbf{x}$ is denoted by

    \begin{equation*} \text{supp}(x) := \{ i: \mathbf{x}_i \ne 0 \} \end{equation*}

    A vector $x$ is referred to as s-sparse if $|\text{supp}(x)| \le s$

  • $\norm{\mathbf{x}}_0$ denotes the number of zero-entries in $\mathbf{x}$
  • $\sigma_1(A) \ge \sigma_2(A) \ge \dots \ge \sigma_{\min \{ m,n \}}(A)$ denote A's singular values

  • Frobenius norm of $A$

    \begin{equation*} \norm{A}_F := \sqrt{\sum_{i, j} A_{ij}^2} = \sqrt{\sum_{i} \sigma_i(A)^2} \end{equation*}

  • Nuclear norm of $A$

    \begin{equation*} \norm{A}_* := \sum_{i} \sigma_i(A) \end{equation*}

  • Spectral norm of $A$

    \begin{equation*} \norm{A}_2 := \max_i \sigma_i(A) \end{equation*}
  • Random variables are denoted with upper-case letters $X, Y$

Definitions

Algebraic Riccati equation

The (algebraic) Riccati equation is problem of finding an unknown matrix $X$ in

  • Continuous case:

    \begin{equation*} A^T X + XA - XB R^{-1} + Q = 0 \end{equation*}

  • Discrete case:

    \begin{equation*} X = A^T X A - \big( A^T X B \big) \big( R + B^T XB \big)^{-1} \big( B^T XA \big) + Q \end{equation*}

where $A$, $B$, $Q$, and $R$ are known real coefficient matrices.

Lagrange multipliers

TODO Modern formulation via differentiable manifolds

Notation

  • $M$ smooth manifold
  • $f : M \to \mathbb{R}$ is a differentiable function we wish to maximize
  • $V \subseteq M$
  • $\varphi : V \to \mathbb{E}^n$ is a local chart

Stuff

By extension of Fermat's Theorem the local maxima are only points where the exterior derivative $df = 0$.

In particular, the extrema are a subset of the critical points of the function $f' = f \circ \varphi^{-1} : U \to \mathbb{R}$.

This is just a mapping from $U \subseteq M$ to

Convex optimization

Visualization

Convexity

  • Interpolation in codomain > interpolation in domain
using Plots, LaTeXStrings, Printf

f(x) = (x - 1) * (x - 2)
x₀, x₁ = 0., 6.


anim = @animate for t = 0:0.01:1
    z = (1 - t) * x₀ + t * x₁

    p = plot(-2:0.05:7, f, label="f(x)", legend=:topleft)
    # title!("Convexity: interpolation in codomain > interpolation in domain")
    vline!([z], label="", linestyle=:dash)
    scatter!([x₀, x₁], [f(x₀), f(x₁)], label="")
    plot!([x₀, x₁], f.([x₀, x₁]),
          label = L"(1 - t) f(x_0) + tf(x_1)",
          annotations = [(x₀ - 0.2, f(x₀), Plots.text(L"f(x_0)", :right, 10)), (x₁ + 0.2, f(x₁), Plots.text(L"f(x_1)", :left, 10))])
    scatter!([z], [f(z)],
             label="",
             annotations = [(z + 0.1, f(z), Plots.text(latexstring(@sprintf("f(%.2f x_0 + %.2f x_1)\\quad", (1 - t), t)), :left, 10))])
    scatter!([z], [(1 - t) * f(x₀) + t * f(x₁)],
             label = "",
             annotations = [(z - 0.1, (1 - t) * f(x₀) + t * f(x₁), Plots.text(latexstring(@sprintf("%.2f f(x_0) + %.2f f(x_1)\\quad", (1 - t), t)), :right, 10))])
end

gif(anim, "test.gif")

Definitions

A convex combination of a set of $n$ vectors $\mathbf{x}_i \in \mathbb{R}^p$ in an arbitrary real space is a vector

\begin{equation*} \mathbf{x}_\theta := \sum_{i=1}^{n} \theta_i \mathbf{x}_i \end{equation*}

where:

  • $\boldsymbol{\theta} = (\theta_1, \dots, \theta_2)$
  • $\theta_i \ge 0$
  • $\sum_{i = 1}^{n} \theta_i = 1$

A convex set is a subset of an affince space that is closed under convex combinations.

More specifically, in a Euclidean space, a convex region is a region where, for every pair of points within the region, every point on the straight line segment that joins the pair of points is also within the region, i.e. we say the set $S$ is a convex set if and only if

\begin{equation*} \begin{split} \forall \mathbf{x}, \mathbf{y} \in S, & \quad \lambda \in [0, 1] \\ (1 - \lambda) \mathbf{x} + \lambda \mathbf{y} & \in S \end{split} \end{equation*}

The boundary of a convex set is always a convex curve, i.e. curve in the Euclidean plane which lies completely on one side of it's tangents.

The intersection of all convex sets containing a given subset $A$ of Euclidean space is called the convex hull of $A$, i.e. the smallest convex set containing the subset $A$.

It's like a "convex closure" of $A$.

A continuously differentiable function $f: \mathbb{R}^p \to \mathbb{R}$ is considered convex if

\begin{equation*} f({y}) \ge f({x}) + \Big\langle \nabla f({x}), {y} - {x} \Big\rangle, \quad \forall {x}, {y} \in \mathbb{R}^p \end{equation*}

In more generality, a continuous function $f$ is convex if for all $x \in \mathbb{R}^p$,

\begin{equation*} \exists g_x: \quad f(y) \ge f(x) + \left\langle g_x, y - x \right\rangle, \quad \forall y \in \mathbb{R}^p \end{equation*}

where the subscript of $g_x$ emphasizes that this vector can depend on $x$. Alternatively, if for all $x, y \in \mathbb{R}^p$,

\begin{equation*} f \Big( tx + (1 - t)y \Big) \le t f(x) + (1 - t) f(y), \quad \forall t \in [0, 1] \end{equation*}

i.e. linear interpolation in input-space is "worse" than linear interpolation in output-space.

A continuously differentiable function $f: \mathbb{R}^p \to \mathbb{R}$ is considered β-strongly convex

\begin{equation*} f({y}) \ge f({x}) + \Big\langle \nabla f({x}), {y} - {x} \Big\rangle + \beta \norm{{x} - {y}}_2^2 \end{equation*}

Similarily to a convex function, we don't require $f$ to be differentiable. In more generality, a contiuous function $f$ is β-strongly convex if for all $x, y \in \mathbb{R}^p$ and for all $t \in [0, 1]$ we have nesterov2009primal

\begin{equation*} f \big( tx + (1 - t)y \big) \le t f(x) + (1 - t) f(y) - \frac{1}{2} \beta \cdot t (1 - t) \norm{x - y}_2^2 \end{equation*}

Contrasting with the definition of a convex function, the only difference is the additional term 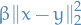$\beta \norm{{x} - {y}}_2^2$.

Quasi-convex and -concave

A quasiconvex function is a function $f: \mathcal{X} \to \mathbb{R}$ such that the preimage $f^{-1} \big( (- \infty, a) \big)$ is a convex set.

To be precise, a function $f: \Omega \to \mathbb{R}$ defined on a convex set $\mathcal{X} \subseteq \mathbb{R}^d$ is quasiconvex if

\begin{equation*} f \big( \lambda x + (1 - \lambda) y \big) \le \max \left\{ f(x), f(y) \right\} \end{equation*}

for all $x, y \in \mathcal{X}$ and $\lambda \in [0, 1]$.

In words, $f$ is quasiconvex then it is always true that a point directly between two other points does not give a higher value of the function than both of the other points do.

A function $f: \mathcal{X} \to \mathbb{R}$ is quasiconcave if we take the above definition and replace convex with concave and $\le$ with $\ge$.

Simplex

A simplex is a generalization of the notion of a triangle or a tetrahedron to arbitrary dimensions.

Specifically, a k-simplex is a k-dimensional polytope which is the convex hull of its $k + 1$ vertices.

More formally, suppose the $k + 1$ points $u_0, \dots, u_k \in \mathbb{R}^k$ are affinely independent, which means $u_1 - u_0, \dots, u_k - u_0$ are linearly independent. Then, the simplex determined by them is the set of points

\begin{equation*} C = \Bigg\{ \theta_0 u_0 + \dots + \theta_k u_k \bigg| \sum_{i=0}^{k} \theta_i = 1 \text{ and } \theta_i \ge 0 \ \forall i \Bigg\} \end{equation*}

Subgradient

Notation

Stuff

We say $g \in \mathbb{R}^n$ is a subgradient of $f: \mathbb{R}^n \to \mathbb{R}$ at $x$ if

\begin{equation*} f(z) \ge f(x) + g^T(z - x), \quad \forall z \end{equation*}

where $g$ replaces the gradient in the definition of a convex function.

Observe that the line $f(x) + g^T(z - x)$ is a global lower bound of $f$.

We say a function $f: \mathbb{R}^n \to \mathbb{R}$ is subdifferentiable at $x$ if there exists at least one subgradient at $x$.

The set of all subgradients at $x$ is called the subdifferential: $\partial f (x)$.

Some remarks:

  • $f$ is convex and differentiable $\implies$ $\partial f(x) = \left\{ \nabla f(x) \right\}$.
  • Any point $x$, there can be 0, 1, or infinitely many subgradients.
  • $\partial f(x) = \emptyset \implies f$ is not convex.

If $0 \in \partial f$, then $x$ is a global minimizer of $f$.

This is easily seen from definition of subgradient, since if $g = 0$, then $f(z) \ge f(x), \forall z$, i.e. global minimizer.

In general there might exist multiple global minimizers.

Subgradient Descent

  1. Suppose $f$ is convex, and we start optimizing at $x_0$
  2. Repeat

    1. Step in a negative subgradient direction:

      \begin{equation*} x = x_0 - t g \end{equation*}

      where $t > 0$ is the step-size and $g \in \partial f(x_0)$.

The following theorem tells us that the subgradient gets us closer to the minimizer.

Suppose $f$ is convex.

  • Let $x = x_0 - tg$ for $g \in \partial f(x_0)$
  • Let $z$ be any point for which $f(z) < f(x_0)$

Then for small enough $t > 0$,

\begin{equation*} || x - z ||_2 < || x_0 - z ||_2 \end{equation*}

i.e. it's a contraction mapping and it has a unique fixed point at

\begin{equation*} z = x^* \in \underset{x}{\text{argmin}}\ f(x) \end{equation*}

That is, the negative subgradient step gets us closer to minimizer.

Suppose $f$ is convex.

  • Let $x = x_0 - tg$ for $g \in \partial f(x_0)$
  • Let $z$ be any point for which $f(z) < f(x_0)$

Then

\begin{equation*} \begin{split} \norm{x - z}_2^2 &= \norm{x_0 - tg - z}_2^2 \\ &= \norm{x_0 - z}_2^2 - 2 t g^T \big( x_0 - z \big) + t^2 \norm{g}_2^2 \\ & \le \norm{x_0 - z}_2^2 - 2 t \big( f(x_0) - f(z) \big) + t^2 \norm{g}_2^2 \end{split} \end{equation*}

where we've used the definition a subgradient to get the inequality above.

Now consider $- 2 t \big( f(x_0) - f(z) \big) + t^2 \norm{g}_2^2$.

  • It's a convex quadration (facing upwards)

  • Has zeros at

    \begin{equation*} t = 0 \quad \text{and} \quad t = \frac{2 \big( f(x_0) - f(z) \big)}{\norm{g}_2^2} > 0 \end{equation*}

  • Therefore, due intermedite value theorem and convexity (facing upwards), we know the term above is negative if

    \begin{equation*} t \in \Bigg( 0, \frac{2 \big( f(x_0) - f(z) \big)}{\norm{g}_2^2} \Bigg) \end{equation*}

    Hence,

    \begin{equation*} \norm{x - z}_2^2 < \norm{x_0 - z}_2^2, \quad x_0 \ne z \end{equation*}

We then observe that if $f$ is Lipschitz, we have

\begin{equation*} \norm{f(x) - f(z)}_2^2 < \alpha \norm{x - z}_2^2 \end{equation*}

with $\alpha \in (0, 1)$, then the subgradient descent using a decreasing step-size is a contraction mapping with a fixed point at $z$! Hence,

\begin{equation*} \lim_{k \to \infty} f \Big( x_{\text{best}}^{(k)} \Big) = f(x^*) \end{equation*}

If we're using a fixed step-size, we cannot guarantee the term considered in the proof of subgradient descent decreasing the objective function is negative (since at some point we get too close to $z$, and so the fixed $t$ we're using is not in the required interval).

That is why we use a decreasing step-size in the theorem above.

Using a fixed step-size, we still have the following bound

\begin{equation*} \lim_{k \to \infty} f \Big( x_{\text{best}}^{(k)} \Big) \le f \big( x^* \big) + \alpha^2 t / 2 \end{equation*}

Cutting-plane method

  • Used in linear integer programming

Consider an integer linear programming problem in standard form as

\begin{equation*} \begin{split} \max_{x}\ & c^T x \\ \text{subject to } & Ax = b \quad x \ge 0, \quad x_i \in \mathbb{Z} \end{split} \end{equation*}

Gomory's cut

A Gomory's cut can be described geometrically as follows:

  1. Drop requirement for $x_i \in \mathbb{Z}$ and solve resulting linear program
    • Solution will be a vertex of the convex polytope consisting of all feasible points
  2. If this vertex is not an integer point
    1. Find a hyperplane with the vertex on one side and all feasible integer points on the other
    2. Add this as an additional linear constraint to exclude the vertex found
    3. Solve resulting linear program
    4. Goto Step 2.0
  3. Fin

One of my first thoughts regarding this was "But how the heck can you separate this vertex from all feasible points with a $\ge$, since lin. prog. can't handle strict inequalities?!".

Solution: it says separating the vertex from all feasible INTEGER points, duh. This is definitively doable if the vertex is non-integer! Great:) Meza happy.

Non-convex optimization

Convex Relaxation

  • Relax problem such that we end up with a convex problem
  • E.g. relaxation of sparse linear regression, you end up with Lasso regression
    • It's really $\ell_1$ regression, but as you can read on that link, it can be viewed as a approximation to the non-convex $\ell_0$ "norm", $\norm{\cdot}_0$ (it's not really a norm)
  • Can sometimes talk about the relaxation gap, which tells how different the optimal convex solution is from the non-convex
  • Relaxation-approach can often be very hard to scale

TODO Convex Projections

Under uncertainty

Stochastic programming

Stochastic Linear Programming

A two-stage stochastic linear program is usually formulated as

\begin{equation*} \begin{split} \min_x & c^T x + \mathbb{E}_{\omega} \big[ Q(x, \omega) \big], \quad x \in X \\ \text{subject to} & \quad Q(x, \omega) = \min f(\omega)^T y \\ & \quad D(\omega) y \ge h(\omega) + T (\omega) x, \quad y \in Y \end{split} \end{equation*}

The first stage of the problem is the minimization above, which is performed prior to the realization of the uncertain parameter $\omega \in \Omega$.

The second stage is finding the variables $y$.

Linear quadratic programming

  • Class of dynamic optimization problems
  • Related to Kalman filter:
    • Recursive formulations of linear-quadratic control problems and Kalman filtering both involve matrix Riccati equations
    • Classical formulations of linear control and linear filtering problems make use of similar matrix decompositions
  • "Linear" part refeers refers to the "motion" of the state
  • "Quadratic" refers to the preferences

Stochastic optimization

TODO

Topics in Convex optimization

Lecture 1

Notation

  • Black-box model: given input $x \in \mathbb{R}^$, a "oracle" returns $f(x)$
  • Complexity of the algorithm is the number of queries made to the black-box oracle

  • Consider Lipschitz functions wrt. infinity-norm, i.e.

    \begin{equation*} \mathcal{F}_L = \left\{ f : [0, 1]^n \to \mathbb{R} \mid \left| f(x) - f(y) \right| \le L \norm{x - y}_{\infty}, \quad \forall x, y \in [0, 1]^n \right\} \end{equation*}

  • Goal: find $\bar{x} \in [0, 1]^n$ s.t.

    \begin{equation*} f(\bar{x}) - f^* \le \varepsilon \end{equation*}

Stuff

There is an algorithm with complexity $\big( \lfloor \frac{L}{2 \varepsilon} \rfloor + 2 \big)^n$ that can achieve the "goal" for all $f \in \mathcal{F}_L$.

Grid search! Let $\big( x_i \big)_{i = 1}^N$ be the grid points, where

\begin{equation*} N = \bigg( \Big\lfloor \frac{L}{2 \varepsilon} \Big\rfloor + 2 \bigg)^n \end{equation*}

is then the number of grid points.

Query $f$ at the grid points $\big( x_i \big)_{i = 1}^N$. Find grid point $\bar{x}$ that achives the minimum of $f$ on $[0, 1]^n$.

Let $\tilde{x}$ be the closest grid point to $x^*$

\begin{equation*} f(\bar{x}) - f^* \le f(\tilde{x}) - f^* \le L \norm{\tilde{x} - x^*} \le L \cdot \frac{\varepsilon}{L} = \varepsilon \end{equation*}

For any algo $A$ that acheives the "goal" for all $f \in \mathcal{F}_L$, there exists an $f \in \mathcal{F}_L$ s.t. on $f$, the algo will require at least $\big( \lfloor \frac{L}{4 \varepsilon} \rfloor \big)^1 - 1$.

Gradient-based

Conjugate Gradient Descent (CGD)

Notation

  • $x_* \in \mathbb{R}^n$ is such that

    \begin{equation*} A x_* = b \end{equation*}

Resources

  • [BROKEN LINK: No match for fuzzy expression: *GP%20&%20Kernel%20stuff]

Setup

Suppose we want to solve the system of linear equations

\begin{equation*} A x = b \end{equation*}

where

  • $x, b \in \mathbb{R}^n$
  • $A \in \mathbb{R}^{n \times n}$ is symmetric and positive-definitive

As it turns out, since $A$ is symmetric and positive-definite we can define an inner product wrt. $A$:

\begin{equation*} \left\langle u, v \right\rangle_A = u^T A v \end{equation*}

We say two vectors $u, v \in \mathbb{R}^n$ are conjugate if they are orthogonal wrt. inner product wrt. $A$, i.e. if

\begin{equation*} \left\langle u, v \right\rangle_A = u^T A v = 0 \end{equation*}

Method (direct)

Let

\begin{equation*} P := \left\{ p_1, \dots, p_n \right\} \end{equation*}

be a set of mutually orthogonal vectors (wrt. $A$), thus $P$ forms a basis of $\mathbb{R}^n$.

We can therefore express $x_*$ in this basis:

\begin{equation*} x_* = \sum_{i=1}^{n} \alpha_i p_i \end{equation*}

Let's consider left-multiplication $A x_* = b$ by $p_k^T$:

\begin{equation*} p_k^T A x_* = p_k^T b \end{equation*}

LHS can be written

\begin{equation*} \begin{split} p_k^T A x_* &= \sum_{i=1}^{n} \alpha_i p_k^T A p_i \\ &= \alpha_k p_k^T A p_k \\ &= \alpha_k \left\langle p_k, p_k \right\rangle_A \\ &= \alpha_k \norm{p_k}_A^2 \end{split} \end{equation*}

where we've let $\norm{p_k}_A$ denote the norm induced by the inner-product wrt. $A$. Therefore:

\begin{equation*} \left\langle p_k, b \right\rangle = \alpha_k \norm{p_k}_A^2 \quad \implies \quad \alpha_k = \frac{\left\langle p_k, b \right\rangle}{\norm{p_k}_A^2} \end{equation*}

Great! These solutions are exact, so why the heck did someone put the term "gradient" into the name?!

Because you might be satisfied with an approximation to the method if this would mean you don't have to find all $n$ of these "conjugate" / orthogonal (wrt. $A$) vectors! This motivatives writing it as a iterative method, which we can terminate when we get some $\varepsilon$ near the true solution.

Iterative

Observe that $x_*$ is actually the unique minimizer of the quadratic $f: \mathbb{R}^n \to \mathbb{R}$

\begin{equation*} f(x) = \frac{1}{2} x^T A x - x^T b \end{equation*}

since

\begin{equation*} \nabla f(x) = A x - b \end{equation*}

The fact that $x_*$ is a unique solution can then be seen by the fact that it's hessian

\begin{equation*} \nabla^2 f(x) = A \end{equation*}

is symmetric positive-definite.

This implies uniqueness of solution only if we can show that

\begin{equation*} x^T A x - x^T b \ge 0, \quad \forall x \ \end{equation*}

Since $A$ is positive-definite, we have

\begin{equation*} x^T A x = x_a \tensor{A}{^{a}_{b}} x^b > 0, \quad \forall x \in \mathbb{R}^n \setminus \left\{ 0 \right\} \end{equation*}

means that all $\tensor{A}{^{a}_{b}} \ge 0$. <= NOT TRUE.

Suppose $\exists i, j = 1, \dots, n$ s.t. $\tensor{A}{^{i}_{j}} &lt; 0$, which also implies $\tensor{A}{^{j}_{i}} = \tensor{A}{^{i}_{j}} &lt; 0$ by symmetry of $A$. Then if $x^i = x^j = 1$ and $x^a = 0$ for $a \notin \left\{ i, j \right\}$, we have

\begin{equation*} \frac{1}{2} x^T A x = \frac{1}{2} x_a \tensor{A}{^{a}_{b}} x^b \begin{cases} \tensor{A}{^{i}_{j}} + \frac{1}{2}(\tensor{A}{^{i}_{i}} + \tensor{A}{^{j}_{j}}) &amp; \text{if } i \ne j \\ \frac{1}{2} (\tensor{A}{^{i}_{i}} + \tensor{A}{^{j}_{j}}) = \tensor{A}{^{i}_{i}} &amp; \text{if } i = j \end{cases} \end{equation*}

If we let $a = b$, it is at least apparent that the diagonals of $A$ has to be non-negative. What about when $a \ne b$? Well, we then need

\begin{equation*} \tensor{A}{^{i}_{i}} + \tensor{A}{^{j}_{j}} &gt; 2 \tensor{A}{^{i}_{j}} \end{equation*}

Since $i, j$ are arbitrary, we require this to hold for all $i, j = 1, \dots, n$ s.t. $i \ne j$.

Great; that's all we need! Since for a symmetric real matrix we can do the eigenvalue decomposition of $A$, i.e.

\begin{equation*} A = V D V^T \end{equation*}

where $D$ is a diagonal matrix with eigenvalues of $A$ as its entries, and $V$ is an orthonormal matrix. Thus

\begin{equation*} x^T A x = (V^T x)^T D (V^T x) = y^T D y \end{equation*}

where we've let $y = V^T x$. We can equivalently consider the case where $y^a = y^b = 1$ and $y^c = 0$ for $c \not\in \left\{ a, b \right\}$. This then proves that the eigenvalues of a symmetric positive-definite matrix $A$ are all positive.

Gradient-free optimization

Random optimization

Idea

\begin{equation*} x_{k + 1} = x_k - h_k \frac{f(x_k + \mu_k u) - f(x_k)}{\mu_k} u \end{equation*}

where

  • $u$ is a random vector distributed, say, uniformly over the unit sphere

This converges under the assumption that $\mu_k \to 0$.

Mirrored descent

Suppose we want to minimize regret

\begin{equation*} R_T(i) := \sum_{t = 1}^{T} \ell_t(I_t) - \ell_t(i) \end{equation*}

where

  • $I_t \in [n]$ is a random variable indicating which index we chose as time $t$
  • $i \in [n]$
  • $\ell_t \in \left\{ 0, 1 \right\}^n$ indicating the loss of 0-1 loss of choosing the corresponding index

One approach is to solving this problem is to

  1. Define a discrete distribution over the indices $[n]$, i.e. $p \in \Delta_n = \left\{ p \in \mathbb{R}^n \mid \sum_{i = 1}^{n} p_i = 1 \right\}$.
  2. Use gradient descent to find the optimal weights $p_i$

TODO: watch first lecture to ensure that you understand the regret-bound for gradient descent

Doing the above naively, leads to the following bound

\begin{equation*} R_T(i) \le \sqrt{T n} \end{equation*}

which unfortunately scales with dimensionality in $\sqrt{n}$.

Mirrored descent takes advantage of the following idea:

  • If we suppose there's one true optimal arm, say $i^*$, then the resulting solution $p^*$ should be "sparse" in the sense that it should only have one non-zero entry, i.e. $p_i^* = 1$ and $p_j = 0$ for $j \ne i^*$.
    • Equivalently, $p^*$ will be a vertex in the simplex $\Delta_n$
  • Naive gradient descent does not make use of this information → want to incorporate this somehow

There's an alternative approach: Franke-Wolfe is a convex-optimization algorithm which aims to point the gradient steps towards verticies.

This works very well for static problems, but in this formulation the function we're evaluating $\ell_t$ is allowed to change wrt. $t$, and apparently this is no good for Franke-Wolfe.

nesterov2013introductory