Fractals
Table of Contents
Notation
Mandelbrot set
The Mandelbrot set is the set complex numbers for which the function

does not diverge when iterated from 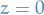 , i.e. remains bounded in absolute value.
, i.e. remains bounded in absolute value.
Formally, the Mandelbrot set is the set of values of  in the complex plane for which the orbit of
in the complex plane for which the orbit of  under iteration of the quadratic map
under iteration of the quadratic map
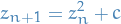
remains bounded.
The Mandelbrot set 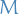 is defined by a family of complex quadratic polynomials
is defined by a family of complex quadratic polynomials

given by

where  is a complex parameter. For each
is a complex parameter. For each  , one considers the behavior of the sequence
, one considers the behavior of the sequence
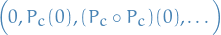
obtained by iteration  starting at critical point
starting at critical point 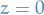 . This either escapes to infinity or stays within a disk of finite radius; the Mandelbrot set is then the set of all points
. This either escapes to infinity or stays within a disk of finite radius; the Mandelbrot set is then the set of all points  such that the sequence stays within a disk of finite radius.
such that the sequence stays within a disk of finite radius.
More formally, if 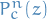 denotes the n-th iterate of
denotes the n-th iterate of  (i.e.
(i.e.  composed with itself
composed with itself  times), the Mandelbrot set is the subset of the complex plane given by
times), the Mandelbrot set is the subset of the complex plane given by
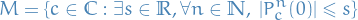
As explained below, it is in fact possible to simplify this definition by taking 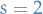 .
.
Visualizations of Mandelbrot sets
- Color all points
 that belong to the Mandelbrot set
that belong to the Mandelbrot set 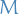 black and all other points white
black and all other points white
Connection to Julia sets
An equivalent definition of the Mandelbrot set is as the subset of the complex plane consisting of those parameters  for which the Julia set of
for which the Julia set of  is connected.
is connected.
Julia set
Let  be a holomorphic function from the Riemann sphere to itself.
be a holomorphic function from the Riemann sphere to itself.
Such  are precisely the complex rational functions, that is
are precisely the complex rational functions, that is
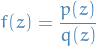
where  and
and  are complex polynomials.
are complex polynomials.
Assume that 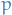 and
and  are non-constant, and that they have no common roots (i.e.
are non-constant, and that they have no common roots (i.e.  does not divide
does not divide 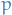 ). Then there is a finite number of open sets
). Then there is a finite number of open sets  , that are left invariant by
, that are left invariant by  and are such that:
and are such that:
 is dense in the plane
is dense in the plane behaves in a regular and equal way on each of the sets
behaves in a regular and equal way on each of the sets 
The last statement means that the termini of the sequences of iterations generated by the points of  are either
are either
- the same set => finite cycle
 are finite cycles of circular or annular shaped sets centered at the same point
are finite cycles of circular or annular shaped sets centered at the same point
These sets  are the Fatou domains of
are the Fatou domains of  , and their union is the Fatou set
, and their union is the Fatou set  of
of  .
.
Further, each of the Fatou domains contains at least on critical point of  , i.e. a (finite) point
, i.e. a (finite) point  such that
such that

if either of the following is the case:
- degree of the numerator
 is at least two larger than the degree of the denominator
is at least two larger than the degree of the denominator 
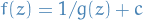 for some
for some  and a rational function
and a rational function  satisfying this condition
satisfying this condition
The complement of the Fatou set  is the Julia set
is the Julia set  of
of  .
.
 is a nowhere dense set (it is without interior points) and an uncountable set (of the same cardinality as the real numbers).
is a nowhere dense set (it is without interior points) and an uncountable set (of the same cardinality as the real numbers).
Like  ,
,  is left invariant by
is left invariant by  , and on this set the iteration is repelling, meaning that
, and on this set the iteration is repelling, meaning that

for all  in a neighborhood of
in a neighborhood of  (within
(within  ).
).
This means that  behaves chaotically on the Julia set.
behaves chaotically on the Julia set.
There are points in the Julia set whose sequence of iterations is finite, there are only a countable number of such points (and thus they only make up a infinitely small part of the Julia set). The sequences generated by points outside this set behave chaotically, a phenomenon called deterministic chaos.
Equivalent definitions of Julia sets are:
 is the smallest closed set containing at least three points which is completely invariant under
is the smallest closed set containing at least three points which is completely invariant under  (Möbius transformation?)
(Möbius transformation?) is the closure of the set of repelling periodic points
is the closure of the set of repelling periodic pointsFor all but at most two points
 , the Julia set is the set of limit points of the full backwards orbit
, the Julia set is the set of limit points of the full backwards orbit
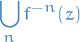
i.e. limit points of the union of pre-images of all the iterations.
- If
 is an entire function, then
is an entire function, then  is the boundary of the set of points which converge to infinity under iteration.
is the boundary of the set of points which converge to infinity under iteration. - If
 is a polynomial, then
is a polynomial, then  is the boundary of the filled Julia set: i.e. those points whose orbits under iterations of
is the boundary of the filled Julia set: i.e. those points whose orbits under iterations of  remain bounded.
remain bounded.
Julia set of a Mandelbrot set
Mandelbrot sets are given by

where  is a complex parameter.
is a complex parameter.
The Julia set of for this system is the subset of complex plane given by:

where  is the n-th iterator of
is the n-th iterator of 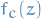 , i.e.
, i.e.  , n times.
, n times.

Figure 1: Source: https://www.wikiwand.com/en/Julia_set