Numerical Recipes

Armadillo test
Random number generation
- Box method Sampling
- Checkpoint 1

Armadillo test

#include <iostream>
#include <armadillo>

using namespace std;
using namespace arma;

int main()
{
  mat m = randn<mat>(4, 5);

  cout << m << endl;

  return 0;
}

Random number generation

Box method Sampling

Algorithm

Let the distribution to generate be $f(x)$
$f(x)$ is defined in the range $[a, b]$
Find a number $y_m$ such that $y_m > \underset{x \in [a, b]}{\max} f(x)$
Generate a random number $x_1 \sim U(0, 1)$
Convert to random number in the range $[a, b]$ by the letting $x_1' = a + (b-a) x_1$
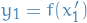
Compute the value $y_1 = f(x_1')$
Generate random number $\alpha \sim U(0, 1)$
Obtain random number in the range $[0, y_m]$ by computing $y_2 = \alpha y_m$
Perform the test: if( y_2 < y_1)
- If true : return $x_1$
- If false : discard $x_1$ and go back to step 4
Repeat steps above until the wanted number of random values have been obtain.

Basically, we end up drawing random numbers in a rectangle box and ONLY keeping the numbers which are under the curve of $f(x)$ .

Code

Main code - C++

#define _USE_MATH_DEFINES

#include <math.h>
#include <iostream>
#include <armadillo>
#include <thread>
#include <fstream>

using namespace std;
using namespace arma;

/**
 * Finds the maximum of the function using coordinate ascent.
 */
template <typename F>
double find_max(F&& f,
                Col<double> initial,
                Col<double> x_min = Col<double>{},
                Col<double> x_max = Col<double>{},
                bool use_xlim = false,
                double alpha = 0.05) {
  if (use_xlim) {
    if (x_min.n_elem != initial.n_elem || x_max.n_elem != initial.n_elem) {
      throw "different dimensions for initial values and limits for x";
    }
    else if (x_min.n_elem != x_max.n_elem) {
      throw "different dimensions for x_min and x_max";
    }
  }

  Col<double> res = vec(initial);

  double x_curr, x_next;
  double y_curr, y_next;

  double x_l, x_r;
  double y_l, y_r;

  uword i;
  do {
    // iterate through each dimension and see if we can obtain a greater y
    for (i = 0; i < res.n_elem; ++i) {
      if (use_xlim) {
        if (res[i] < x_min[i]) {
          res[i] = x_min[i];
        }
        else if (res[i] > x_max[i]) {
          res[i] = x_max[i];
        }
      }
      x_curr = res[i];
      y_curr = f(res);

      // candidate x's
      x_l = x_curr - alpha;
      x_r = x_curr + alpha;      

      // compute candidate y's
      res[i] = x_l;
      if (use_xlim) {
        if (res[i] < x_min[i]) {
          res[i] = x_min[i];
        }
        else if (res[i] > x_max[i]) {
          res[i] = x_max[i];
        }
      }
      y_l = f(res);

      res[i] = x_r;
      if (use_xlim) {
        if (res[i] < x_min[i]) {
          res[i] = x_min[i];
        }
        else if (res[i] > x_max[i]) {
          res[i] = x_max[i];
        }
      }
      y_r = f(res);

      // check if best candidate y is better
      x_next = y_l < y_r ? x_r : x_l;
      res[i] = x_next;
      y_next = f(res);

      if (y_next <= y_curr) {
        // new y is worse => reset to old x
        res[i] = x_curr;
      }
    }

    // output
    // cout << y_curr << endl;
  } while(y_next > y_curr);

  return f(res);
}

void test_find_max() {
  double maximum = 100;
  Col<double> a = randu<Col<double>>(1);

  const auto f = [&maximum](Col<double> v) -> double {
    if (abs(sum(v)) > maximum) {
      return maximum;
    }
    else {
      return abs(sum(v));
    }
  };

  // trying out `find_max`
  double y_m = find_max(f, a);

  cout << "Maximum: " << y_m << endl;
}

/** INTEGRATION METHODS */
enum SAMPLING_METHOD {
  BOX_METHOD = 0
};

template <typename F, uint N>
struct IntegrationArgs {
  F&& f;
  uint num_samples;
  int n_jobs;
  SAMPLING_METHOD sampling_method; // sampling_method to use for integration
  Col<double> x_min;
  Col<double> x_max;
  double y_m;                      // at least the maximum of the function being passed

  bool save = false;               // specifies whether or not to save the xs and ys

  IntegrationArgs(F&& func) : f(func) { }
};

/**
 * Wrapper to enable type-deduction for the `IntegrationArgs`.
 * 
 * https://stackoverflow.com/a/797632
 */
template <uint N, typename F>
IntegrationArgs<F, N> integration_args(F&& func,
                                       Col<double> x_min,
                                       Col<double> x_max,
                                       double y_max = 0,
                                       bool auto_find_max = false,
                                       SAMPLING_METHOD sampling_method = BOX_METHOD,
                                       int n_jobs = 1,
                                       bool save = false) {
  auto args = IntegrationArgs<F, N>(func);
  args.x_min = x_min;
  args.x_max = x_max;
  args.num_samples = N;
  args.sampling_method = sampling_method;
  args.n_jobs = n_jobs;

  args.save = save;

  if (auto_find_max) {
    // create an starting-point for finding the maximum value of the function in this domain
    Col<double> initial = randu<Col<double>>(x_min.n_elem); // U(0, 1)
    initial %= (x_min - x_max);                               // U(0, b - a)
    initial += x_max;                                        // U(a, b) = a + U(0, b - a)

    cout << initial << endl;
    args.y_m = find_max(func, initial) + 0.05;  // adding an extra constant for good measure
  }
  else {
    args.y_m = y_max;
  }


  // return IntegrationArgs<F, N>(func, x_min, x_max, y_max, find_max, sample_method, n_jobs);
  return args;
}

template <uint N, typename F>
IntegrationArgs<F, N> integration_args(F&& func,
                                       Col<double> x_min,
                                       Col<double> x_max,
                                       SAMPLING_METHOD sampling_method = BOX_METHOD,
                                       int n_jobs = 1) {
  return integration_args<N, F>(func, x_min, x_max, 0, true, sampling_method, n_jobs);
}

template <uint N, typename F>
IntegrationArgs<F, N> integration_args_persist(F&& func,
                                       Col<double> x_min,
                                       Col<double> x_max,
                                       SAMPLING_METHOD sampling_method = BOX_METHOD,
                                       int n_jobs = 1) {
  auto a = integration_args<N, F>(func, x_min, x_max, 0, true, sampling_method, n_jobs);
  a.save = true;
  return a;
}

template <uint N, typename F>
ostream& dump(ostream &o, const IntegrationArgs<F, N>& args) {
  o << "Integration arguments:" << endl;
  o << "Domain:\n" << args.x_min << " " << args.x_max << endl;
  o << "Num samples: " << args.num_samples << endl;
  return o;
}


/**
 * Samples from UNDER a function using the "box sampling_method".
 */
template <typename F, uint K>
Col<double> _box_method_sampling(IntegrationArgs<F, K> args) {
  Col<double> a = args.x_min;
  Col<double> b = args.x_max;

  double y_m = args.y_m;

  Col<double> x_1;
  double y_1;
  double y_2;

  uint N = 1000;
  Col<double> results = zeros(N);
  uint i;
  for (i = 0; i < N; ++i) {
    do {
      x_1 = a + (b - a) % randu<vec>(size(a)); // draw new random input
      y_1 = args.f(x_1);                       // compute f(x)
      y_2  = randu() * y_m;                    // comparison value
    } while (y_2 >= y_1);                      // keep going until we have a valid value

    results[i] = y_1;
  }

  return results;
}

/**
 * Using samples from UNDER the function, compute the integral using the Riemann sum.
 */
template <typename F, uint N>
double monte_carlo_integration(IntegrationArgs<F, N> args) {
  Col<double> a = args.x_min;
  Col<double> b = args.x_max;
  Col<double> range = b - a;

  double y_m = args.y_m;
  cout << "Maximum value for f used in integration: " << y_m << endl;

  Col<double> x_1;
  double y_1;
  double y_2;

  dump(cout, args);

  uint inside = 0;
  uint i;

  if (args.save) {
    Mat<double> out_x_1 = zeros(N);
    Col<double> out_y_1 = zeros(N);
    Col<double> out_y_2 = zeros(N);

    for (i = 0; i < N; ++i) {
      x_1 = a + range % randu<Col<double>>(size(a)); // draw new random input
      y_1 = args.f(x_1);                             // compute f(x)
      y_2  = randu() * y_m;                          // comparison value

      if (y_2 < y_1) {
        inside++;
      }

      // store values      
      out_x_1[i] = x_1[0];
      out_y_1[i] = y_1;
      out_y_2[i] = y_2;
    }

    out_x_1.save("x_1.txt", csv_ascii);
    out_y_1.save("y_1.txt", csv_ascii);
    out_y_2.save("y_2.txt", csv_ascii);
  }
  else {
    for (i = 0; i < N; ++i) {
      x_1 = a + range % randu<Col<double>>(size(a)); // draw new random input
      y_1 = args.f(x_1);                             // compute f(x)
      y_2  = randu() * y_m;                          // comparison value

      if (y_2 < y_1) inside++;
    }
  }

  cout << "Range: " << range << endl;

  double ratio = ((double)inside) / N;
  cout << "Monte Carlo integration: [" << inside << " / " << N << "] " << ratio << endl;

  // compute area of box
  Col<double> diff = b - a;

  // this is just a `reduce`, since an actual `reduce` is only available from C++17
  double tot = y_m;  // "height"
  std::for_each(std::begin(diff), std::end(diff), [&tot](double v) {
      tot *= v;  // "widths"
  });

  cout << "Box 'volume': " << tot << endl;

  return ratio * tot;
}


/**
 * Wrapper around multiple sampling_method of integration, which is specified in the `args`.
 */
template <typename F, uint N>
Col<double> integrate(IntegrationArgs<F, N> args) {
  switch (args.sampling_method) {
    case BOX_METHOD: {
      return Col<double>{monte_carlo_integration(args)};
    }
    default:
      throw "invalid sampling_method of integration specified";
  }
}

/** END INTEGRATION METHODS */


/** Gaussian distribution */
class MyGaussian
{
public:
  Col<double> mu;
  Mat<double> sigma;

  //! Default constructor
  MyGaussian(Col<double> mean, Mat<double> variance) : mu(mean), sigma(variance) {
    _sigma_det = det(variance);
    _sigma_inv = inv(variance);
  };


  double evaluate(Col<double> x);
  double integralAnalytic();

  template <uint N>
  Col<double> integralNumeric();

protected:
private:
  // to not have to recompute these each time
  double _sigma_det;
  Mat<double> _sigma_inv;

  double _domain_width = 10;  // can't integrate to and from infinity
};

double MyGaussian::evaluate(Col<double> x) {
  Col<double> diff = this->mu - x;

  // apparently we're not supposed the normalization constant...

  // double z = 1.0 / sqrt(2 * M_PI * this->_sigma_det);
  // return (z * exp(- 0.5 * diff.t() * this->_sigma_inv * diff))[0];

  return exp(- 0.5 * diff.t() * this->_sigma_inv * diff)[0];
}

template <uint N>
Col<double> MyGaussian::integralNumeric() {
  auto f = [&](Col<double> x) {
    return this->evaluate(x);
  };

  const auto job_args = integration_args<N>(f, this->mu - this->_domain_width * this->_sigma_det,
                                            this->mu + this->_domain_width * this->_sigma_det,
                                            BOX_METHOD);
  return integrate(job_args);
}


double MyGaussian::integralAnalytic() {
  // assuming we're integrating from -\infty to \infty
  return (this->_sigma_det) * sqrt(2 * M_PI);
}


/**
 * Simple test for the `MyGaussian` class
 */
void test_my_gaussian() {
  Col<double> mu = zeros(1);
  Mat<double> sigma = eye(1, 1);
  auto g = new MyGaussian(mu, sigma);
  cout << "Gaussian parameters: "
       << "mu = " << g->mu
       << "sigma = " << g->sigma << endl;

  auto numerical = g->integralNumeric<10000>();
  cout << "f(x) = " << g->evaluate(zeros(1)) << endl
       << "Numerical integration: " << numerical[0] << endl
       << "Size of numerical integration " << size(numerical) << endl
       << "Analytical integration: " << g->integralAnalytic() << endl;
}

/** END MyGaussian */


int main()
{
  test_find_max();

  // the Gaussian stuff
  test_my_gaussian();

  // // setup for parallel Monte-Carlo integration
  // const int N = 100000000;
  // const int n_jobs = 3;
  // const int n_per_job = N / n_jobs;
  // const auto job_args = integration_args<n_per_job>(f, x_min, x_max,BOX_METHOD);

  // Col<double> runs[n_jobs];
  // thread threads[n_jobs];
  // int i;

  // // start jobs
  // for (i = 0; i < n_jobs; ++i) {
  //   threads[i] = thread([i, &job_args,&runs]() {
  //       runs[i] = integrate(job_args);
  //     });
  // }

  // // gather results
  // for (i = 0; i < n_jobs; ++i) {
  //   threads[i].join();
  //   cout << "Integral " << i << ": " << runs[i];
  // }

  return 0;
}

Maximum: 100
Gaussian parameters: mu =         0
sigma =    1.0000

   4.9904

Maximum value for f used in integration: 1.04995
Integration arguments:
Domain:
  -10.0000
    10.0000

Num samples: 10000
Range:    20.0000

Monte Carlo integration: [1199 / 10000] 0.1199
Box 'volume': 20.9991
f(x) = 1
Numerical integration: 2.51779
Size of numerical integration 1x1
Analytical integration: 2.50663

Visualization

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# load data
x_1 = np.loadtxt("x_1.txt")
y_1 = np.loadtxt("y_1.txt")
y_2 = np.loadtxt("y_2.txt")

# plot it
mask = y_1 > y_2
xs = x_1
xs_true = np.linspace(-10, 10, x_1.shape[0])
ys_true = norm.pdf(xs_true, 0, 1)
xs_in = xs[mask]
xs_out = xs[~mask]
ys_in = y_1[mask]
ys_out = y_1[~mask]

ratio = y_2[mask].shape[0] / y_2.shape[0]
box = np.max(y_1) * (np.max(xs) - np.min(xs))
z = ratio * box

# plt.scatter(xs_out, ys_in)
# plt.scatter(xs_in, ys_out)
plt.scatter(xs[mask], y_2[mask] / z, s=1)
plt.scatter(xs[~mask], y_2[~mask] / z, s=1)
plt.plot(xs_true, ys_true, label="$\mathcal{N}(0, 1)$")
plt.legend()
plt.show()

print(z)

Bugs

DONE Apparently I'm drawing examples if they're ON the curve, not UNDER

No. Well yes, but that was because I was drawing all the points where $y_1 > y_2$ , which is NOT what I ought to. The points UNDER the curve is of course $\forall y_2 : y_2 \le y_1$ where $y_1$ is literally values evaluated for $f(x)$ !
DONE Got the wrong integral

Well, I wasn't. I was of course already divinding by the normalization factor, i.e. the integral, and thus I got the wrong result compared to their unnormalized integral… So the code worked, I just compared with the wrong values.

Checkpoint 1

Code

Main code

#define _USE_MATH_DEFINES

#include <math.h>
#include <iostream>
#include <armadillo>
#include <fstream>

using namespace std;
using namespace arma;

/**
 * Finds the maximum of the function using coordinate ascent.
 */
template <typename F>
double find_max(F&& f,
                Col<double> initial,
                Col<double> x_min = Col<double>{},
                Col<double> x_max = Col<double>{},
                bool use_xlim = false,
                double alpha = 0.05,
                uword max_steps = 1000) {
  if (use_xlim) {
    if (x_min.n_elem != initial.n_elem || x_max.n_elem != initial.n_elem) {
      throw "different dimensions for initial values and limits for x";
    }
    else if (x_min.n_elem != x_max.n_elem) {
      throw "different dimensions for x_min and x_max";
    }
  }

  Col<double> res = vec(initial);

  double x_curr, x_next;
  double y_curr, y_next;

  double x_l, x_r;
  double y_l, y_r;

  uword cnt = 0;
  uword i;
  do {
    // iterate through each dimension and see if we can obtain a greater y
    for (i = 0; i < res.n_elem; ++i) {
      if (use_xlim) {
        if (res[i] < x_min[i]) {
          res[i] = x_min[i];
        }
        else if (res[i] > x_max[i]) {
          res[i] = x_max[i];
        }
      }
      x_curr = res[i];
      y_curr = f(res);

      // candidate x's
      x_l = x_curr - alpha;
      x_r = x_curr + alpha;      

      // compute candidate y's
      res[i] = x_l;
      if (use_xlim) {
        if (res[i] < x_min[i]) {
          res[i] = x_min[i];
        }
        else if (res[i] > x_max[i]) {
          res[i] = x_max[i];
        }
      }
      y_l = f(res);

      res[i] = x_r;
      if (use_xlim) {
        if (res[i] < x_min[i]) {
          res[i] = x_min[i];
        }
        else if (res[i] > x_max[i]) {
          res[i] = x_max[i];
        }
      }
      y_r = f(res);

      // check if best candidate y is better
      x_next = y_l < y_r ? x_r : x_l;
      res[i] = x_next;
      y_next = f(res);

      if (y_next <= y_curr) {
        // new y is worse => reset to old x
        res[i] = x_curr;
      }
    }

    cnt++;
    // output
    // cout << y_curr << endl;
  } while(y_next > y_curr && cnt < max_steps);

  return f(res);
}

void test_find_max() {
  double maximum = 100;
  Col<double> a = randu<Col<double>>(1);

  const auto f = [&maximum](Col<double> v) -> double {
    if (abs(sum(v)) > maximum) {
      return maximum;
    }
    else {
      return abs(sum(v));
    }
  };

  // trying out `find_max`
  double y_m = find_max(f, a);

  cout << "Maximum: " << y_m << endl;
}

/** Sampling */

template <typename F>
struct SamplingArgs {
  F&& f;
  Col<double> x_min;
  Col<double> x_max;
  double y_m;

  uint n_samples = 1000;
  int n_jobs = 1;
  bool save = false;
  string out_filename = "samples.txt";

  SamplingArgs(F&& func) : f(func) { }
};


template <typename F>
SamplingArgs<F> sampling_args(F&& func, Col<double> x_min, Col<double> x_max, uint n_samples = 1000, bool save = false) {
  auto a = SamplingArgs<F>(func);
  a.x_min = x_min;
  a.x_max = x_max;
  a.n_samples = n_samples;
  a.save = save;

  a.y_m = find_max(a);

  return a;
}


template <typename F>
double find_max(SamplingArgs<F> arg) {
  Col<double> initial = randu<Col<double>>(arg.x_min.n_elem); // U(0, 1)
  initial %= (arg.x_min - arg.x_max);                         // U(0, b - a)
  initial += arg.x_max;                                       // U(a, b) = a + U(0, b - a)
  return find_max(arg.f, initial, arg.x_min, arg.x_max, true, 0.001, 10000) + 0.05;
}


/**
 * Samples from UNDER a function using the "box sampling_method".
 */
template <typename F>
Mat<double> box_method_sampling(SamplingArgs<F> args) {
  Col<double> a = args.x_min;
  Col<double> b = args.x_max;

  double y_m = args.y_m;

  Col<double> x_1;
  double y_1;
  double y_2;

  uint i;
  uword j;
  mat result = zeros<mat>(args.n_samples, a.n_elem + 1); // (n, p + 1)
  for (i = 0; i < args.n_samples; ++i) {
    do {
      x_1 = a + (b - a) % randu<vec>(size(a)); // draw new random input
      y_1 = args.f(x_1);                       // compute f(x)
      y_2  = randu() * y_m;                    // comparison value
    } while (y_2 >= y_1);                      // keep going until we have a valid value

    for (j = 0; j < x_1.n_elem; ++j) {
      result(i, j) = x_1[j];
    }
    result(i, j) = y_2;
  }

  return result;
}

/** END Sampling */

/** Checkpoint 1 */
double exponential(double lambda, double x) {
  return lambda * exp(- lambda * x);
}

void test_exponential(double lambda, uint n) {
  auto x_min = Col<double>{ 0 };
  auto x_max = Col<double>{ 20 };
  auto f = [lambda](Col<double> x) { return lambda * exp(- lambda * x[0]); };
  auto args = sampling_args(f, x_min, x_max, n, true);
  args.y_m = 1;
  args.out_filename = "samples_test.txt";
  auto out = box_method_sampling(args);

  out.save(args.out_filename, raw_ascii);
}


int main() {
  // test_find_max();

  // sampling from an exponential
  // test_exponential(1 / 2.2, 1000);

  double lambda = 1 / 2.2;
  uint n = 1000 * 500;

  auto x_min = Col<double>{ 0 };
  auto x_max = Col<double>{ 20 };

  auto f = [lambda](Col<double> x) { return lambda * exp(- lambda * x[0]); };
  auto args = sampling_args(f, x_min, x_max, n, true);

  cout << "y_m: " << args.y_m << endl;

  cout << "Sampling...";
  auto out = box_method_sampling(args);
  cout << "OK" << endl;

  cout << "Saving to file " << args.out_filename << "...";
  out.save(args.out_filename, raw_ascii);
  cout << "OK" << endl;
}

y_m: 0.504752 Sampling…OK Saving to file samples.txt…OK

Visualization

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# parameters
n_experiments = 500
n_per_experiment = 1000

# load data
data = np.loadtxt("samples.txt")
runs = data.reshape(-1, n_per_experiment, 2)
means = runs.mean(axis=1)

single_experiment_std = runs[0, :, 0].std()
single_experiment_mean = runs[0, :, 0].mean()
print("Std. error of the mean for single experiment of {} samples: {:.5f} ± {:.5f}".format(
    n_per_experiment,
    single_experiment_mean,
    single_experiment_std / np.sqrt(n_per_experiment)
))

all_experiments_std = means[:, 0].std()
all_experiments_mean = means[:, 0].mean()
print("Std. error of the mean over {} experiments of {} samples: {:.5f} ± {:.5f}".format(
    n_experiments,
    n_per_experiment,
    all_experiments_mean,
    all_experiments_std / np.sqrt(n_per_experiment)
))

fig, axes = plt.subplots(2, figsize=(15, 8))
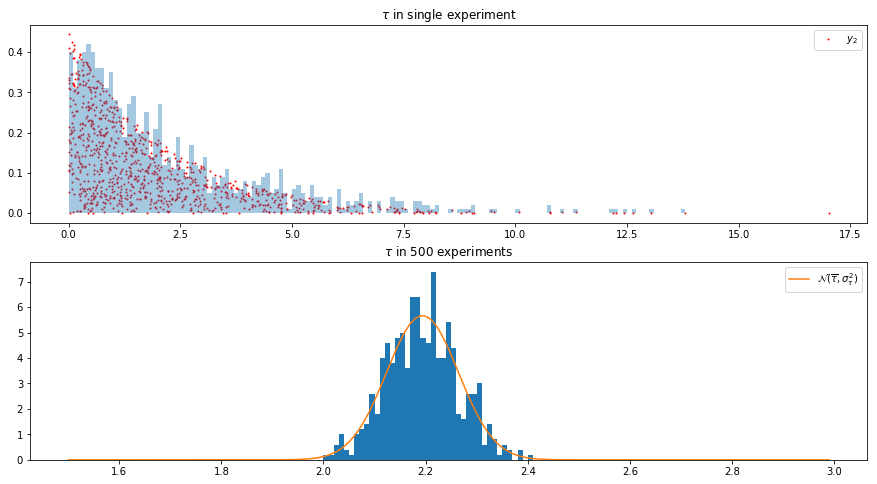
axes[0].set_title(r"$\tau$ in single experiment")
axes[0].hist(runs[0, :, 0], np.arange(0, 15, 0.1), normed=True, alpha=0.4)
axes[0].scatter(runs[0, :, 0], runs[0, :, 1], s=1, c="r", label="$y_2$")

axes[1].set_title(r"$\tau$ in 500 experiments")
axes[1].hist(means[:, 0], np.arange(1.5, 3, 0.01), normed=True)

xs = np.arange(1.5, 3, 0.01)
axes[1].plot(xs, norm.pdf(xs, loc=all_experiments_mean,
                          scale=all_experiments_std),
             label=r"$\mathcal{N}(\overline{\tau}, \sigma_\tau^2)$")

axes[0].legend()
axes[1].legend()
fig

Questions

How well can you expect to measure the true lifetime from 1 experiment?

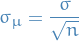
$\begin{equation*} \sigma_\mu = \frac{\sigma}{\sqrt{n}} \end{equation*}$

and then

$\begin{equation*} \mu \pm \sigma_\mu \end{equation*}$

is the std. error of the mean.

How well can you expect to measure the true lifetime from 500 experiments?

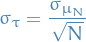
$\begin{equation*} \sigma_\tau = \frac{\sigma_{\mu_N}}{\sqrt{N}} \end{equation*}$

and then

$\begin{equation*} \tau \pm \sigma_\tau \end{equation*}$

is the std. error of the mean.

Numerical Recipes

Table of Contents

Armadillo test

Random number generation

Box method Sampling

Algorithm

Code

Main code - C++

Visualization

Bugs

Checkpoint 1

Code

Main code

Visualization

Questions

How well can you expect to measure the true lifetime from 1 experiment?

How well can you expect to measure the true lifetime from 500 experiments?