Thermodynamics

Table of Contents

Notation

  • $Q$ is heat / thermal energy
  • $U$ is internal energy

Equations / Laws

Zeroth Law

If each of two systems is in thermal equilibrium with a third system they are in thermal equilibrium with each other.

First Law of Thermodynamics

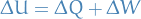
\begin{equation*} \Delta U = \Delta Q + \Delta W \end{equation*}

Maxwell-Boltzmann distribution

\begin{equation*} f(v) = \sqrt{\left(\frac{m}{2 \pi kT}\right)^3}\, 4\pi v^2 e^{- \frac{mv^2}{2kT}} \end{equation*}

Compressibility

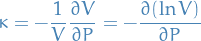
\begin{equation*} \kappa = - \frac{1}{V} \frac{\partial V}{\partial P} = - \frac{\partial (\ln V)}{\partial P} \end{equation*}

Bulk modulus

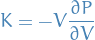
\begin{equation*} K = - V \frac{\partial P}{\partial V} \end{equation*}

Heat capacity

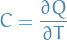
\begin{equation*} C = \frac{\partial Q}{\partial T} \end{equation*}

Thermal expansivity

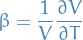
\begin{equation*} \beta = \frac{1}{V} \frac{\partial V}{\partial T} \end{equation*}

Bernoulli Equation

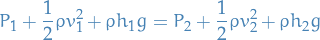
\begin{equation*} P_1 + \frac{1}{2}\rho v_1^2 + \rho h_1 g = P_2 + \frac{1}{2}\rho v_2^2 + \rho h_2 g \end{equation*}

Ideal gas law

\begin{equation*} PV = n RT = N k_B T \end{equation*}

Work (reversible process)

"Derivation"

thermodynamics_work_reversible_fig.png

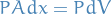
\begin{equation*} P A dx = P dV \end{equation*}

which gives us

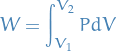
\begin{equation*} W = \int_{V_1}^{V_2} P dV \end{equation*}

Differential

\begin{equation*} dW = - P dV \end{equation*}

where work is defined as the work done ON the system by its surroundings .

TODO Boltzmann Distribution

\begin{equation*} \frac{\langle N_i \rangle}{N} = \frac{g_i}{e^{(\varepsilon_i - \mu) / kT}} = \frac{1}{Z} g_i e^{\varepsilon_i / kT} \end{equation*}

In the case where we have no degeneracy (or you simply care about the probability of specific state corresponding to some energy $ε$i instead of the probability of the energy $\varepsilon_i$ itself, i.e. don't want to included all possible states which can take on the this energy):

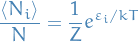
\begin{equation*} \frac{\langle N_i \rangle}{N} = \frac{1}{Z} e^{\varepsilon_i / kT} \end{equation*}

Notation

  • $\langle N_i \rangle$ is the expected number of particles in the energy level indexed by $i$
  • $N$ total number of particles
  • $\varepsilon_i$ the energy of the ith energy level
  • $g_i$ is the degeneracy of the ith energy level with energy $\epsilon_i$ (this is always an integer), which corresponds to the number of quantum mechanical observables which can take on an energy of $\epsilon_i$

Derivation

Source

In our deduction we're going to consider a microcanonical ensemble.

To begin with, we ignore the problem of degeneracy; i.e. we assume there is only one way to put $N_i$ particles into the energy level $\varepsilon_i$.

The number of possible ways to "bin" the particles in the different energies:

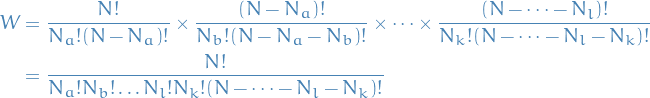
\begin{equation*} \begin{split} W &= \frac{N!}{N_a! (N - N_a)!} \times \frac{(N - N_a)!}{N_b! (N - N_a - N_b)!} \times \dots \times \frac{(N - \dots - N_l)!}{N_k! (N - \dots - N_l - N_k)!} \\ &= \frac{N!}{N_a! N_b! \dots N_l! N_k! (N - \dots - N_l - N_k)!} \end{split} \end{equation*}

where each of the factor on the first line represents the number of possible ways to partition all $N$ particles into groups of $N_a$, then the rest of the particles partitioned into bins of size $N_b$, and so on. I.e. we end up counting the number of possible ways to partition all $N$ particles into the different "energy-bins" with $N_i$ particles in the ith "energy-bin".

Because we're "exhausting" the number of particles, i.e. we keep "binning" until we have no particles left (each particle MUST be assigned a bin), then $(N - \dots - N_l - N_k)! = 0! = 1$, and we can write

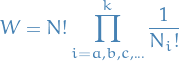
\begin{equation*} W = N! \prod_{i=a, b, c, ...}^k \frac{1}{N_i!} \end{equation*}

Which is just the multinomial coefficient , the number of ways to arrange $N$ objects into $k$ bins, ignoring order / permutations.

Now we want to take into account the possible degeneracy degree $\varepsilon$ of each energy level. The $N_i$ corresponding to the energy $\varepsilon_i$ can then be arranged in $g_i^{N_i}$ ways within the energy-level (since for each particle with energy $\varepsilon_i$ can go in either of the $g_i$ "sub-bins"). Thus,

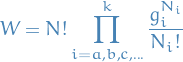
\begin{equation*} W = N ! \prod_{i=a, b, c, \dots}^k \frac{g_i^{N_i}}{N_i!} \end{equation*}

BUT when doing this we're treating the particles as distinguishable , i.e. the order of arranging into the "sub-bins" matter, which leads to a "invalid" entropy (not extensive , which means that the entropy is not proportional to the amount of substance, which it really ought to be). This is called the Gibbs paradox. This leads to the Bose-Einstein expression for 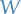$W$ :

\begin{equation*} W = \prod_i \frac{(N_i + g_i - 1)!}{N_i!(g_i - 1)!} \end{equation*}

NOT FINISHED YET DUE TO REALIZING THIS NOT FITTING AS WELL INTO AN ANKI CARD AS I HAD HOPED.

Adiabatic expansion

\begin{equation*} P V^{\gamma} = \text{constant} \end{equation*}

Clapeyron equation

\begin{equation*} \frac{dp}{dT} = \frac{S_m^\text{vap} - S_m^\text{liq}}{V_m^\text{vap} - V_m^\text{liq}} \quad \text{and} \quad \frac{dp}{dT} = \frac{S_m^\text{liq} - S_m^\text{sol}}{V_m^\text{liq} - V_m^\text{sol}} \end{equation*}

Which is basically saying that when we're moving between two phases, the change in pressure 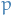$p$ wrt. temperature $T$ is equal to the ratio between the change in entropy and volume.

TODO Derivation

Van der Waals equation

\begin{equation*} \big(p + \frac{a}{V_m^2} \big) \big( V_m - b \big) = RT \end{equation*}

TODO Derivation

Lennard-Jones potential

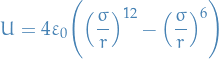
\begin{equation*} U = 4 \varepsilon_0 \Bigg( \Big( \frac{\sigma}{r} \Big)^{12} - \Big( \frac{\sigma}{r} \Big)^6 \Bigg) \end{equation*}

where the first term is the repulsion and the second term is the Van der Waals forces.

Ionic bonding

\begin{equation*} U(r) = 1.481 \varepsilon \Big[ \pm \Big(\frac{\sigma}{r} \Big) + \Big(\frac{\sigma}{r} \Big)^9 \Big] \end{equation*}
  • assumes single and complete ionisation, which is why we can consider the pairwise potential as the Coloumb force (1st term) together with a repulsive force (2nd term)
  • attraction via electron exchanges to produces filled orbitals results in charged particles that attract

Surface energy

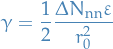
\begin{equation*} \gamma = \frac{1}{2} \frac{\Delta N_\text{nn} \varepsilon}{r_0^2} \end{equation*}

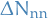where $\varepsilon$ is the seperation energy and $\Delta N_\text{nn}$ is the change in nearest neighbours .

TODO Derivation

Capillary rise

Viscosity

Viscosity characterizes the sheer forces that exist in a moving fluid.

For a gas we have

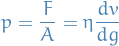
\begin{equation*} p = \frac{F}{A} = \eta \frac{dv}{dg} \end{equation*}

Reynolds number

\begin{equation*} R_e = \frac{\text{interial forces}}{\text{viscous forces}} \end{equation*}

Braggs Law

\begin{equation*} 2 d \sin \theta = \lambda n \end{equation*}

Miller indices

Index system tused to identify equally-spaced parallel planes intersecting lattice points.

It works as follows:

If the plane intercepts at:

  • $\frac{a}{h}$ along the x-axis
  • $\frac{b}{k}$ along the y-axis
  • $\frac{c}{l}$ along the z-axis

the the lattice has Miller indices $(hkl)$

Entropy

\begin{equation*} dS = \frac{d Q_\text{rev}}{T} \end{equation*}

Or with a fixed energy, for a system in a particular macrostate , defined by the number of associated micro-states $\Omega$ :

\begin{equation*} S = k_B \ln \Omega \end{equation*}

Internal energy

\begin{equation*} dU = T dS - p dV \end{equation*}

This is true regardless of whether or not the process is reversible!

Gibbs function

The function

Is a state-function.

\begin{equation*} G = H - TS \end{equation*}

and

\begin{equation*} dG = Vdp - SdT \end{equation*}

Criterion for spontanous process

\begin{equation*} \Delta G \le 0 \end{equation*}

and in equilibrium

\begin{equation*} \Delta G = 0 \end{equation*}

Enthalpy

Is a state-function.

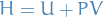
\begin{equation*} H = U + PV \end{equation*}

and

\begin{equation*} dH = T dS + V dp \end{equation*}

Helmholtz function

\begin{equation*} F = U - TS \end{equation*}

and

\begin{equation*} dF = - S dT - p dV \end{equation*}

Second Law of Thermodynamics

\begin{equation*} dS \ge 0 \end{equation*}

for any process, in total. That is,

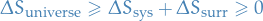
\begin{equation*} \Delta S_\text{universe} \ge \Delta S_\text{sys} + \Delta S_\text{surr} \ge 0 \end{equation*}

Maxwell's relations

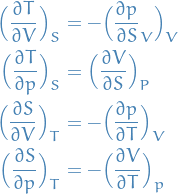
\begin{equation*} \begin{split} \Big( \frac{\partial T}{\partial V} \Big)_S &= - \Big( \frac{\partial p}{\partial S}_V \Big)_V \\ \Big( \frac{\partial T}{\partial p} \Big)_S &= \Big( \frac{\partial V}{\partial S} \Big)_P \\ \Big( \frac{\partial S}{\partial V} \Big)_T &= - \Big( \frac{\partial p}{\partial T} \Big)_V \\ \Big( \frac{\partial S}{\partial p} \Big)_T &= - \Big( \frac{\partial V}{\partial T} \Big)_p \end{split} \end{equation*}

Definitions

Temperature

The temperature of a system is a property that determines whether or not that system would be in thermal equilibrium with other systems.

Equilibrium state

An equilibrium state is one in which all the bulk physical properties do not change with time and are uniform throughout the system

Young's Modulus

Young's modulus is a measure of the ability of a material to withstand changes in length when under lengthwise tension or compression.

Systems

Closed system

Cannot exchange matter with its surroundings, but may exchange energy.

Isolated system

No exchange of any material or energy with surroundings.

Reversible process

A process where every step for the system and its surroundings can be reversed. A reversible process involves a series of equilibrium states.

Path-independent integral over $P$ wrt. $V$ for an ideal gas (this is true for any state variables )

Ensembles

Microcanonical ensemble

A microcanonical ensemble is a mechanical ensemble which represents the possible states of the particles in a system where the total energy of the system is exactly known .

Grand canonical ensemble

A grand canonical ensemble is the statistical ensemble that is used to represent the possible states of a mechanical system of particles that is being maintained in thermodynamic equilibrium (thermal and chemical) with a reservoir.

Canonical ensemble

A canonical ensemble is the statistical ensemble that is used to represent the possible states of a mechanical system in thermal equilibrium with a heat bath at a fixed temperature. The system can exchage energy with the heat bath, so that the states of the system will differ in total energy.

Adiabatic process

A adiabatic process is a reversible and adiathermal (thermally isolated) process.

Bonding

Covalent bonding

Strong and directional based bonding based on electron-sharing .

Metallic bonding

Attraction of like species via sharing of free electrons.

It's similar to covalent , but the electrons are completely delocalized and free to move.

Hydrogen bonding

Hydrogen atom itself is shared between atoms.

Isotropic

A process is called isotropic if 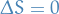$\Delta S = 0$.