Quantum Mechanics
Table of Contents
- Reading
- Progress
- Definitions
- Stuff
- Zero point energy
- Quantum Harmonic Oscillator
- Correspondance principle
- Operators
- Coherence
- Observables
- Momentum
- Angular momentum
- Angular momentum - reloaded
- Central potential
- Hydrogen atom
- Spin - intrinsic angular momentum
- Addition of angular momenta
- Identical Particles
- Fourier Transforms and Uncertainty Relations
- Bra, kets, and matrices
- Time-independent Perturbation Theory
- Time-dependent Perturbation Theory
- Radiation
- Quantum Scattering Theory
- Central Field Approximation
- Variational Method
- Hidden Variables, EPR Paradox, Bell's Inequality
- Quantum communication
- Quantum computing
- Cohen-Tannoudji - Quantum Mechanics
- Principles of Quantum Mechanics - Dirac
- Quantum Theory for Mathematicians
- Notation
- 2. A First Approach to Classical Mechanics
- 3. A First Approach to Quantum Mechanics
- 4. The Free Schrödinger Equation
- 5. A Particle in a Square Well
- 6. Perspectives on the Spectral Theorem
- 7. Spectral Theorem for Bounded Self-Adjoint Operators
- 8. Spectral Theorem for Bounded Self-Adjoint Operators: Proofs
- Practice problems
- Q & A
Reading
- Quantum Physics - Stephen Gasiorowicz
- "Quantum Physics", Messiah, p. 463 Appendix A: Distributions & Fourier Transform
Progress
- Note taken on
p. 115
Definitions
Words
- plane wave
- multi-dimensional wave
- wave packet
- superposition of plane waves
- hilbert space
- Banach space withe addition of an inner product
- banach space
- Space with metric, and is complete wrt. to the metric in a sense that each Cauchy sequence converges to a limit within the space.
- isotropic
- Independent of orientation.
Bound / unbound wave equations
Bound energy
Restricts us to positive energies 
Unbound energy
Allows both positive and negative energies 
Schrödinger equation
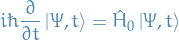
Operators
Position operator

Russel-Sanders notation
States that arise in coupling orbital angular momentum  and spin
and spin  to give total angular momentum
to give total angular momentum  are denoted:
are denoted:

where the  is "optional" (not always included).
is "optional" (not always included).
Further, remember that we often use the following notation to denote the different angular momentum  :
:
Stuff
Zero point energy
Heisenbergs uncertainty principle tells us that a particle cannot sit motionless at the bottom of it's potential well, as this would imply that the uncertainty in momentum  would be infinite. Therefore, the lowest-energy state of the system (called ground state ) must be a distribution for the position and momentum which at all times satisfy the uncertainty principle.
would be infinite. Therefore, the lowest-energy state of the system (called ground state ) must be a distribution for the position and momentum which at all times satisfy the uncertainty principle.
Near the bottom of a potential well, the Hamiltonian of a general system (the quantum-mechanical operator giving a system its energy) can be approximated as a quantum harmonic oscillator:
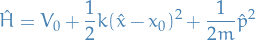
Quantum Harmonic Oscillator
![\begin{equation*}
\hat{H} = \Bigg[ - \frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} + \frac{1}{2} m \omega^2 x^2 \Bigg]
\end{equation*}](../../assets/latex/quantum_mechanics_7c9244b8b792fc892f30045f30726f21b7065032.png)
Thus, the eigenvalue function of the Hamiltonian becomes
![\begin{equation*}
\Bigg[ - \frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} + \frac{1}{2} m \omega^2 x^2 \Bigg] \psi = E \psi
\end{equation*}](../../assets/latex/quantum_mechanics_2f748733cb811a4375991e37f90dfb46653a92b6.png)
As it turns out, this differential equation has the eigenfunctions:

where  denote the n-th [BROKEN LINK: No match for fuzzy expression: *Hermite%20polynomials], with
denote the n-th [BROKEN LINK: No match for fuzzy expression: *Hermite%20polynomials], with  .
.
Further, using the raising and lowering operators discussed in Angular momentum - reloaded we can rewrite the solutions as
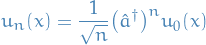
Annihiliation / lowering operator:
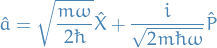
Creation / Raising operator:

Solution
There's two ways of going about this:
- Solving using the ladder operators, but you somehow need to obtain the ground levels
- Solving using straight up good ole' method of variation of parameters and Sturm-Liouville theory
Solving using ladder-operators
- Notation
 is the eigenfunction corresponding to the n-th eigenvalue
is the eigenfunction corresponding to the n-th eigenvalue 
 , which is dimensionless
, which is dimensionless , which is dimensionless
, which is dimensionless

- Stuff
The Hamiltonian in this case is given by
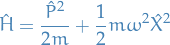
with the TISE

For convenience we rewrite the Hamiltonian
![\begin{equation*}
\begin{split}
\hat{H} &= \hbar \omega \Bigg[ \frac{\hat{P}^2}{2 m \hbar \omega} + \frac{m \omega}{2 \hbar} \hat{X}^2 \Bigg] \\
&= \hbar \omega \Big[ \hat{\eta}^2 + \hat{\xi}^2 \Big]
\end{split}
\end{equation*}](../../assets/latex/quantum_mechanics_1b9eb857df709299df3905ea14d5e3c26105ae1c.png)
But
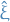 and
and  do not commute:
do not commute:
![\begin{equation*}
[ \hat{\xi}, \hat{\eta} ] = \frac{i}{2}
\end{equation*}](../../assets/latex/quantum_mechanics_bc97facb3df45546b6eb9ea1c63fdc884d279f40.png)
So we instead use the notation of
 and
and  which have the property
which have the property
![\begin{equation*}
[ \hat{a}, \hat{a}^\dagger ] = 1
\end{equation*}](../../assets/latex/quantum_mechanics_437cd4aa86dd5274e5e835448fe308d9ced59efa.png)
Once again rewriting the Hamiltonian

Observe that
![\begin{equation*}
[ \hat{H}, \hat{a} ] = - \hbar \omega \ \hat{a}
\end{equation*}](../../assets/latex/quantum_mechanics_c327ba7d4fd17a0a95440c738d7aa8b70d19d63b.png)
Conider the following operation:
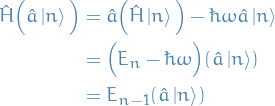
where we in the last line used the fact that for a simple Harmonic Oscillator
 .
.
Thus,

I.e. applying
 to an eigenfunction
to an eigenfunction  gives us the eigenfunction of the
gives us the eigenfunction of the  eigenstate.
eigenstate.
We call this operator the annhiliation or lowering operator.
We can do exactly the same of
 to observe that
to observe that

which is why we call
 the creation or rising operator.
the creation or rising operator.
Buuut there's a problem: we can potential "annihilate" below to a state with energy below zero! To fix this we simply define the ground state such that
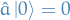
Thus,
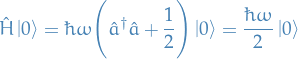
And all other higher energy states can then be constructed from this, by successsive application of

- Normalizing the lowering- and raising-operator
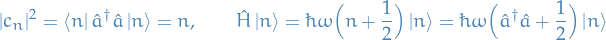
Thus,
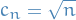
Doing the same for
 , we get
, we get
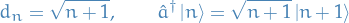
- Solving for the ground-state
We can find the proper solution for the ground-state by solving the differential equation
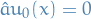
And substituting in for
 both the
both the 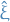 and
and  , so that we get the differential equation. Solving this, we get
, so that we get the differential equation. Solving this, we get

- Normalizing the lowering- and raising-operator
Solving the differential equation
We start of by rewriting the Schrödinger equation for the harmonic oscillator:
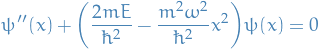
Letting  , we have
, we have
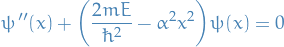
We'll require our solution to be normalizable, i.e. square-integrable, therefore we need the differential equation to be satisfied as  , in which case we can drop the constant term:
, in which case we can drop the constant term:
Letting  which is just a constant (apparently…), we have
which is just a constant (apparently…), we have
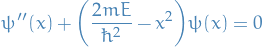
I'm not sure I'm "cool" with this. There's clearly something weird going on here, since  is a parameter of the potential, NOT a variable which we can just set.
is a parameter of the potential, NOT a variable which we can just set.
Letting 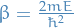 , we then have
, we then have

Therefore we instead consider the simpler problem:
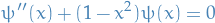
where we've dropped the  , which we will include later on through the us of method of variation of parameters. This clearly has the solution
, which we will include later on through the us of method of variation of parameters. This clearly has the solution
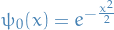
Now, using method of variation of parameters, we suppose there exists some particular solution of the form:

For which we have
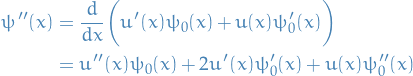
Substituting into the diff. eqn. involving  ,
,

Since  satisfies the original equation, we have
satisfies the original equation, we have
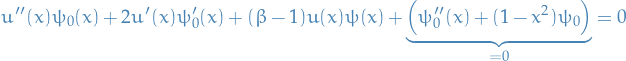
Seeing this, we substitute in our solution for  ,
,
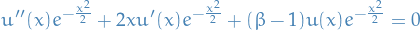
Thus,
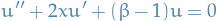
Which, if we let
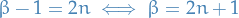
gives us

which we recognize as Hermite differential equation! Hence, we have the solutions

Why the  though? Well, if you attempt to solve the Hermite equation above using a series solution, i.e. assuming
though? Well, if you attempt to solve the Hermite equation above using a series solution, i.e. assuming
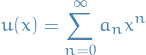
you end up seeing that you'll have a recurrence relation which depends on the integer  , and further that for this to be square-integrable we require the series to terminate for some
, and further that for this to be square-integrable we require the series to terminate for some  , hence you get that dough above.
, hence you get that dough above.
Also, it shows us that we do indeed have a (countably) infinite number of solutions, as we'd expect from a Sturm-Liouville problem such as the Schrödinger equation :)
Correspondance principle
The correspondence principle states that the behavior of systems described by quantum mechanics reproduces the classical physics in the limit of large numbers.
Operators
Momentum
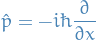
"Derivation"
Considering the wave equation of a free particle, we have
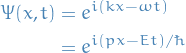
Taking the derivative of the above, and rearranging, we obtain:
![\begin{equation*}
p \big[ \Psi(x, t) \big] = - i \hbar \frac{\partial}{\partial x} \big[ \Psi(x, t) \big]
\end{equation*}](../../assets/latex/quantum_mechanics_e9d4453e606f945090485ae9d0290df6002f09da.png)
and thus we have the momentum operator
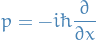
Hamiltonian
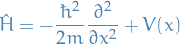
"Derivation"
Where the Hamiltonian comes from the fact that for TISE we have the following:
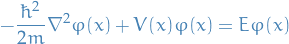
which we can then write as:
![\begin{equation*}
\Big[ - \frac{\hbar^2}{2m} \nabla^2 + V(x) \Big] \varphi(x) = E \varphi(x)
\end{equation*}](../../assets/latex/quantum_mechanics_8bb0ba994b3bb23184cb1145a8f97a41fbf95342.png)
and we have our operator  !
!
In the above "derivation" of the Hamiltonian, we assume TISE for convenience. It works equally well with the time-dependence, which is why we can write the TIDE expression using the Hamiltonian.
In fact, one can deduce it from writing the wave-function as a function of  and
and  , and then note the operator defined for the momentum
, and then note the operator defined for the momentum  . This operator can then be substituted into the classical formula for the energy to provide use with a definition of the Hamiltonian operator.
. This operator can then be substituted into the classical formula for the energy to provide use with a definition of the Hamiltonian operator.
Theorems
Conserved operators
A time-independent operator is conserved if and only if ![$[\hat{H}, \hat{O}] = 0$](../../assets/latex/quantum_mechanics_0e8e7c400c52fc780f5169d1701b8510b3d8e98a.png) , i.e. it commutes with the Hermitian operator.
, i.e. it commutes with the Hermitian operator.
Coherence
Stack excange answer
This guy provides a very nice explanation of quantum coherence and entanglement.
Basically what he's saying is that coherence refers to the case where the wave-functions which are superimposed to create the wave-function of the particle under consideration have a definite phase difference , i.e. the phase-difference between the "eigenstates" is does not change wrt. time and is not random .
Another answer to the same question says:
"It is better to think of there being one and only one wavefunction that describes all the particles in the universe."
Which is trying to make sense of entanglement, saying that we can look at the "joint probability" of e.g. two particles and based on measurement taken from one particle we can make a better judgement of the probability-distribution of the measurement of the other particle. At least this is how I interpret it.
Observables
Each dynamic variable is associated with a linear operator, say  , and it's expectation can be computed:
, and it's expectation can be computed:
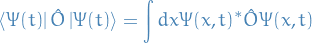
when there is no ambiguity about the state in which the average is computed, we shall write

The possible outcomes of an observable is given by the eigenvalue of the corresponding operator  , i.e. the solutions of the eigenvalue equation:
, i.e. the solutions of the eigenvalue equation:

where  is the eigenstate corresponding to the eigenvalue
is the eigenstate corresponding to the eigenvalue  .
.
Observables as Hermitian operators
Observables are required to be Hermition operators, i.e. operators such that for the operator 

where  is called the Hermitian conjugate of
is called the Hermitian conjugate of  .
.
We an operator corresponding to an Observable to be a Hermitian operator as this is the only way to ensure that all the eigenvalues of the corresponding operator are real, and we want our measurements to be real, of course.
Compatilibity Theorem
Given two observables  and
and  , represented by the Herimitian operators
, represented by the Herimitian operators 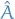 and
and  , then the following statements are equivalent:
, then the following statements are equivalent:
 and
and  are compatible
are compatible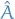 and
and  have a common eigenbasis
have a common eigenbasis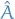 and
and  commute, i.e.:
commute, i.e.: ![$[\hat{A}, \hat{B}] = 0$](../../assets/latex/quantum_mechanics_81fb46d729367fa031cd2235cf831733ac641fb3.png)
Generalised Uncertainty Relation
If  and
and  denote the uncertainties in observables
denote the uncertainties in observables  and
and  respectively in the state
respectively in the state  , then the generalised uncertainty relation states that
, then the generalised uncertainty relation states that

Momentum
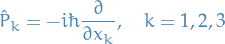
Then
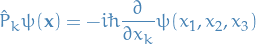
And we have commutability, and thus the we can interchange the order of derivation
![\begin{equation*}
[ \hat{P}_k, \hat{P}_l ] = 0 \quad \iff \quad \frac{\partial^2}{\partial x_k \partial x_l} \psi(\mathbf{x}) = \frac{\partial^2}{\partial x_l \partial x_k} \psi(\mathbf{x})
\end{equation*}](../../assets/latex/quantum_mechanics_7658b0d23bc723beff7c1a5c272a23ed3ccbe578.png)
and
![\begin{equation*}
[\hat{X}_k, \hat{P}_l ] = i \hbar \delta_{k l}
\end{equation*}](../../assets/latex/quantum_mechanics_a027de200f6a6bd03149d7d3e73a77262e3bc648.png)
Hence,
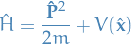
where
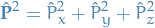
Separation of variables
Here we consider the TISE for a isotropic harmonic oscillator in 3 dimensions, for which the potential is
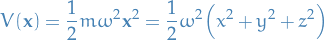
We can then factorize the Hamiltonian in the following way
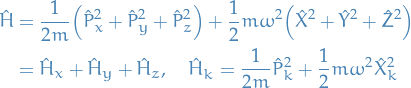
Using this in the Schrödinger equation, we get

And we then assume that we can express 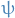 as
as

which gives us
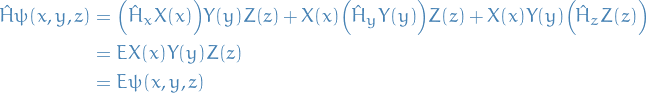
Which gives us
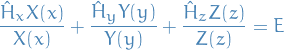
And since  is a constant, we can write
is a constant, we can write  , which gives us a system of equations
, which gives us a system of equations
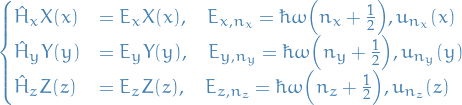
where  denotes the eigenfunction in the k-th dimension for the n-th quantised energy-level (remember we're working with a harmonic osicallator).
Which gives
denotes the eigenfunction in the k-th dimension for the n-th quantised energy-level (remember we're working with a harmonic osicallator).
Which gives

where  denotes the factors of the Hermite polynomials.
denotes the factors of the Hermite polynomials.
Angular momentum


Commutation
The interesting thing about the angular momentum operators, is that unlike the position- and momentum-operators in different dimensions does not commute!
![\begin{equation*}
[ \hat{L}_i, \hat{L}_j ] = i \hbar \ \varepsilon_{ijk} \hat{L}_k
\end{equation*}](../../assets/latex/quantum_mechanics_f8bde5f495abd6e1ba2602cd2d88deb66c4bf878.png)
This implies that the angular momentum in different dimensions are not compatible observables, i.e. we cannot observe one without affecting the distribution of measurements for the other!
Square of the angular momentum
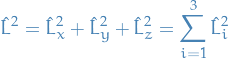
or in spherical coordinates,
![\begin{equation*}
\hat{L}^2 = - \hbar^2 \Bigg[ \frac{1}{\sin \theta} \frac{\partial}{\partial \theta} \Big( \sin \theta \frac{\partial}{\partial \theta} \Big) + \frac{1}{\sin^2 \theta} \frac{\partial^2}{\partial \phi^2} \Bigg]
\end{equation*}](../../assets/latex/quantum_mechanics_e278815117a1879fd90a7bb09ce03062e544f1c5.png)
We then observe that  is compatible with any of the Cartesian components of the angular momentum:
is compatible with any of the Cartesian components of the angular momentum:
![\begin{equation*}
[\hat{L}^2, \hat{L}_x] = [\hat{L}^2, \hat{L}_y] = [\hat{L}^2, \hat{L}_z] = 0
\end{equation*}](../../assets/latex/quantum_mechanics_fe55448db26b86f1a2a21359463590e941836788.png)
which also tells us that they have a common eigenbasis / simultaneous eigenfunctions .
Angular momentum operators in spherical coordinates
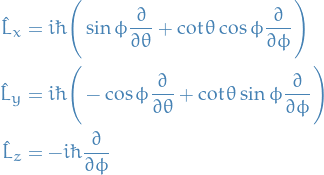
Eigenfunctions
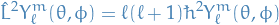
where 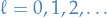 and
and
![\begin{equation*}
Y_{\ell}^m (\theta, \phi) = (-1)^m \Bigg[ \frac{2 \ell + 1}{4 \pi} \frac{(\ell - m)!}{(\ell + m)!} \Bigg]^{-1/2} P_{\ell}^m ( \cos \theta ) e^{im \phi}
\end{equation*}](../../assets/latex/quantum_mechanics_6b0080c4bd12192170ef19bf5522f169365a378f.png)
with 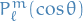 known as the associated Legendre polynomials.
known as the associated Legendre polynomials.
![\begin{equation*}
Y_{\ell}^m (\theta, \phi) = (-1)^m \Bigg[ \frac{2 \ell + 1}{4 \pi} \frac{(\ell - m)!}{(\ell + m)!} \Bigg]^{-1/2} P_{\ell}^m ( \cos \theta ) e^{im \phi}
\end{equation*}](../../assets/latex/quantum_mechanics_6b0080c4bd12192170ef19bf5522f169365a378f.png)
with 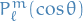 known as the associated Legendre polynomials.
known as the associated Legendre polynomials.
Quantisation of angular momentum
The eigenvalue function for the magnitude of the angular momentum tells us that the angular momentum is quantised. The square of the magnitude of the angular momentum can only assume one of the discrete set of values
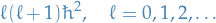
and the z-component of the angular momentum can only assume one of the discrete set of values

for a given value of  .
.
Laplacian operator

Angular momentum - reloaded
We move away from the notation of using  for angular momentum because what follows is true for any operator satisfying these properties.
for angular momentum because what follows is true for any operator satisfying these properties.
To generalize what the raising and lowering operators we found for the angular momentum we let  denote an (Hermitian) operator which satisfies the following commutation relations:
denote an (Hermitian) operator which satisfies the following commutation relations:
![\begin{equation*}
[\hat{J}_k, \hat{J}_\ell ] = i \hbar \varepsilon_{k \ell m} \hat{J}_m, \qquad \hat{J}^2 = \sum_{k} \hat{J}_k^2, \qquad [ \hat{J}^2, \hat{J}_k ] = 0
\end{equation*}](../../assets/latex/quantum_mechanics_0d94e73b27f56d9bfa0d4ca74705817023e31037.png)
And since  and
and  are compatible, we know that these have a common eigenbasis, which we denote
are compatible, we know that these have a common eigenbasis, which we denote  , and we write the eigenvalues in the following form:
, and we write the eigenvalues in the following form:
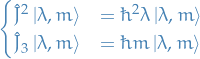
Further, we introduce the raising and lowering operators defined by:
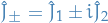
for which we can compute the following properties:
![\begin{equation*}
[ \hat{J}^2, \hat{J}_\pm ] = 0
\end{equation*}](../../assets/latex/quantum_mechanics_114b4d8c8dc48f5d8a1bf1fe7d3a0b3e011ede3c.png)
![\begin{equation*}
[ \hat{J}_3, \hat{J}_\pm ] = \pm \hbar \hat{J}_{\pm}
\end{equation*}](../../assets/latex/quantum_mechanics_b83e24ac7ccf18b9fc35a2c0ee7b44e4a132c084.png)
I.e. we're working with a raising operator for  .
.
Considering the action of the commutator 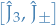 on an eigenstate
on an eigenstate  , we obtain the following:
, we obtain the following:


which tells us that both 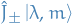 are also eigenstates of the
are also eigenstates of the  but with eigenvalues
but with eigenvalues  , unless
, unless  .
.
Thus  and
and  act as raising and lowering operators for the z-component of
act as raising and lowering operators for the z-component of  .
.
Further, notice that since  we have
we have

Hence, the eigenstates generated by the action of  are still eigenstates of
are still eigenstates of  belonging to the same eigenvalue
belonging to the same eigenvalue  . Thus, we can write
. Thus, we can write
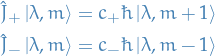
where  are proportionality constants.
are proportionality constants.
The notation used for the eigenstates  is simply saying that we know that the eigenvalue for
is simply saying that we know that the eigenvalue for  does not change under the operator
does not change under the operator  , and thus only the eigenvalue corresponding to
, and thus only the eigenvalue corresponding to  changes with the factor
changes with the factor  (or rather another term of
(or rather another term of  ) and so we denote this new eigenstate as
) and so we denote this new eigenstate as  .
.
To generalize the raising and lowering operators we found for the angular momentum we let  denote an (Hermitian) operator which satisfies the following commutation relations:
denote an (Hermitian) operator which satisfies the following commutation relations:
![\begin{equation*}
[\hat{J}_k, \hat{J}_\ell ] = i \hbar \varepsilon_{k \ell m} \hat{J}_m, \qquad \hat{J}^2 = \sum_{k} \hat{J}_k^2, \qquad [ \hat{J}^2, \hat{J}_k ] = 0
\end{equation*}](../../assets/latex/quantum_mechanics_0d94e73b27f56d9bfa0d4ca74705817023e31037.png)
And since  and
and  are compatible, we know that these have a common eigenbasis, which we denote
are compatible, we know that these have a common eigenbasis, which we denote  , and we write the eigenvalues in the following form:
, and we write the eigenvalues in the following form:
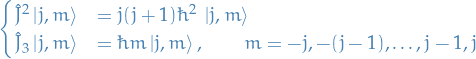
with 
The set of  states
states  is called a multiplet.
is called a multiplet.
We introduce the raising and lowering operators defined by:
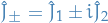
for which we can compute the following properties:
![\begin{equation*}
[ \hat{J}^2, \hat{J}_\pm ] = 0
\end{equation*}](../../assets/latex/quantum_mechanics_114b4d8c8dc48f5d8a1bf1fe7d3a0b3e011ede3c.png)
![\begin{equation*}
[ \hat{J}_3, \hat{J}_\pm ] = \pm \hbar \hat{J}_{\pm}
\end{equation*}](../../assets/latex/quantum_mechanics_b83e24ac7ccf18b9fc35a2c0ee7b44e4a132c084.png)
And we have the relations:
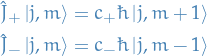
with
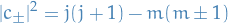
or, if we're assuming  , we have
, we have
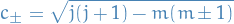
There was originally also the relation

which I somehow picked up from the lecture. But I'm not entirely sure what this actually means…
Some proofs
Lowering operator on an eigenstate is another eigenstate


Where the RHS is due to the commutation relation we deduced earlier. This gives us the equation
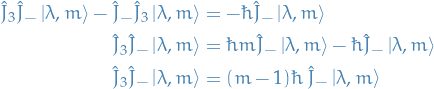
which tells us that  is also an eigenstate of
is also an eigenstate of  but with the eigenvalue
but with the eigenvalue 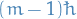 .
.
Just to make it completely obvious what we're saying, we can write the relation above as:

Eigenvalues are bounded
The eigenvalues of  are bounded above and below, or more specifically
are bounded above and below, or more specifically

Further, we have the following properties:
Eigenvalues of
 are
are 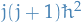 , where
, where  is one of the allowed values
is one of the allowed values
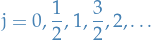
 thus we label the eigenstates of
thus we label the eigenstates of  and
and  by
by  rather than by
rather than by  , so that
, so that
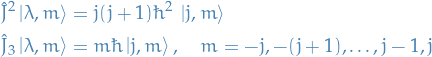
- For an eigenstate
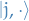 , there are
, there are  possible eigenvalues of
possible eigenvalues of 
The set of  states
states  is called a multiplet
is called a multiplet
We start by observing the following:
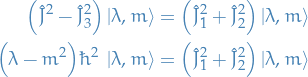
Taking the scalar product with  yields
yields

so that

Hence the spectrum of  is bounded above and below, for a given
is bounded above and below, for a given  . We can deduce that
. We can deduce that
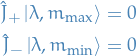
Using the following relations:
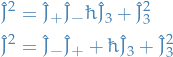
and applying the  to
to  and
and  in turn, we can obtain the following relations:
in turn, we can obtain the following relations:

Using the notation  and using the equality above, we get the equation
and using the equality above, we get the equation
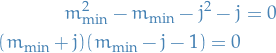
and we see that, since  by definition, the only acceptable root to the above quadratic is
by definition, the only acceptable root to the above quadratic is

Now, since  and
and  differ by some integer,
differ by some integer,  , we can write
, we can write

Or equivalently,

Hence, the allowed values are
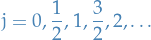
for any given value of  , we see that
, we see that  ranges over the values
ranges over the values

which is a total of  values.
values.
Concluding the following:
Eigenvalues of
 are
are 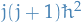 , where
, where  is one of the allowed values
is one of the allowed values
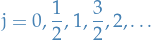
Since
 we can equally well label the simultaneous eigenstates of
we can equally well label the simultaneous eigenstates of  and
and  by
by  rather than by
rather than by  , so that
, so that
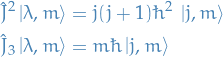
- For a eigenvalue of
 , there are
, there are  possible eigenvalues of
possible eigenvalues of  , denoted by
, denoted by  , where
, where  runs from
runs from  to
to 
- The set of
 states
states  is called a multiplet
is called a multiplet
- Which step makes it so that the j in the case of "normal" angular momentum only takes on integer values?
In the case where we're working with "normal" angular momentum, the spherical harmonics are also eigenfunctions
 . Since we require that the wave function must be single-valued, the spherical coordinates must be periodic in
. Since we require that the wave function must be single-valued, the spherical coordinates must be periodic in  with period
with period  :
:

this implies that
 is an integer, hence
is an integer, hence  must also be an integer.
must also be an integer.
Properties of J
 implies
implies

I.e.
 , thus
, thus  is positive definite
is positive definite
 such that
such that
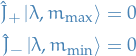
This is :
![\begin{equation*}
\begin{split}
\hat{J}_+ \hat{J}_- &= (\hat{J}_1 + i \hat{J}_2) (\hat{J}_1 - i \hat{J}_2) \\
&= \hat{J}_1^2 + \hat{J}_2^2 + i [\hat{J}_2, \hat{J}_1] \\
&= \hat{J}^2 - \hat{J}_3^2 + \hbar \hat{J}_3
\end{split}
\end{equation*}](../../assets/latex/quantum_mechanics_911ceee78d27d219e0244df53696cbbeaab6bfa0.png)
and
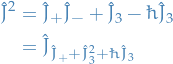
:
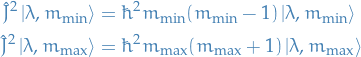
 ,
,  implies that
implies that 
Normalization constant
Computing the matrix elements
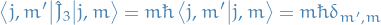
The matrix is 
And for the raising and lowering operators
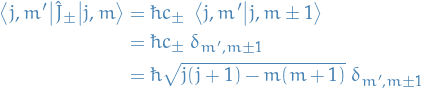
Q & A
DONE Which step makes it so that the j in the case of "normal" angular momentum only takes on integer values?
In the case where we're working with "normal" angular momentum, the spherical harmonics are also eigenfunctions  . Since we require that the wave function must be single-valued(?), the spherical coordinates must be periodic in
. Since we require that the wave function must be single-valued(?), the spherical coordinates must be periodic in  with period
with period  :
:

this implies that  is an integer, hence
is an integer, hence  must also be an integer.
must also be an integer.
I'm not sure what they mean by "single-valued". From the notes they do this:

of which I'm not entirely sure what they mean.
From looking at looking at the spherical harmonics from a [BROKEN LINK: No match for fuzzy expression: *Spherical%20harmonics] the eigenvalue 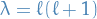 for some non-negative integer
for some non-negative integer  , is due to regularity on the poles
, is due to regularity on the poles  .
.
Central potential
Notation
 is the angle vertical to the xy-plane
is the angle vertical to the xy-plane is the angle in the xy-plane
is the angle in the xy-plane is the mass (avoids confusion with the magnetic quantum number
is the mass (avoids confusion with the magnetic quantum number  )
) is the position vector
is the position vector denotes the magnitude of the position vector
denotes the magnitude of the position vector
Stuff
![\begin{equation*}
\Bigg[ - \frac{\hbar^2}{2 \mu} \nabla^2 + V(r) \Bigg] u(\mathbf{r}) = E u(\mathbf{r})
\end{equation*}](../../assets/latex/quantum_mechanics_13bbbaed0b51bcbaa3c90d5ffd6342c6a32f24fc.png)
In spherical coordinates we write the Laplacian as

we can then rewrite this in terms of the angular momentum operator:

and thus the TISE becomes
![\begin{equation*}
\frac{h^2}{2 \mu} \Big[ - \frac{1}{r^2} \frac{\partial}{\partial r} \Big( r^2 \frac{\partial}{\partial r} \Big) + \frac{1}{\hbar^2 r^2} \hat{L}^2 \Big] u(r, \theta, \phi) = \big(E - V(r) \big) u(r, \theta, \phi)
\end{equation*}](../../assets/latex/quantum_mechanics_11e638756cc41efa66c97d677103f28bd6280626.png)
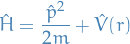
where  , then any pair of
, then any pair of 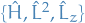 commutes, so there exists a set of simultaneous eigenstates
commutes, so there exists a set of simultaneous eigenstates 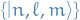 .
.
Hydrogen atom
Notation
 effective mass of system
effective mass of system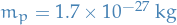

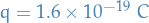

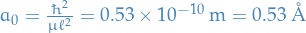
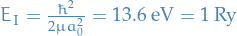
 is the Bohr radius
is the Bohr radius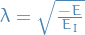

Stuff
Superposition of eigenstates of proton and electron
(Coloumb) potential:
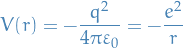
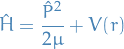
where the effective mass is
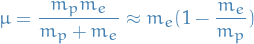
The TISE is:
![\begin{equation*}
\Big[ - \frac{\hbar^2}{2 \mu} \nabla^2 + V(r) \Big] \Psi(\mathbf{x}) = E \Psi(\mathbf{x})
\end{equation*}](../../assets/latex/quantum_mechanics_ed915b37098138dd5f7f255de76794f6f6c99b51.png)
We make the ansatz: 
Thus,
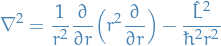
Thus, we end up with
![\begin{equation*}
\Bigg[ \frac{\hbar^2}{2 \mu}\frac{d^2}{dr^2} - \frac{e^2}{r} + \frac{\hbar^2 \ell (\ell + 1)}{2 \mu r^2} \Bigg] \chi_{\ell}(r) = E \chi_{\ell} (r), \quad \chi_\ell(0) = 0
\end{equation*}](../../assets/latex/quantum_mechanics_5d7a57dcaaf7ea61855fd930d4fbea34b21a8e8c.png)
and we let
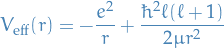
We now introduce some "scales" for length and energy:
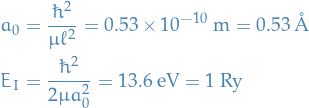
where  is the Bohr radius. Further, we let
is the Bohr radius. Further, we let
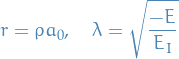
Substituting these scales into the TISE deduced earlier:
![\begin{equation*}
\Bigg[ - \frac{\hbar^2}{2 \mu} \frac{1}{a_0^2} \frac{d^2}{d \rho^2} + \frac{\hbar^2 \ell (\ell + 1)}{2\mu a_0^2 \rho^2} - \frac{e^2}{a_0 \rho} - E \Bigg] \chi_{\ell}(a_0 \rho) = 0
\end{equation*}](../../assets/latex/quantum_mechanics_cb7a6f560631a5a4b60a73735b6382ba8d308cb2.png)
![\begin{equation*}
- E_I \Bigg[ - \frac{d^2}{d \rho^2} - \frac{\ell (\ell + 1)}{\rho^2} + \frac{2}{\rho} + \frac{E}{E_I} \Bigg] \chi_{\ell} (a_0 \rho) = 0
\end{equation*}](../../assets/latex/quantum_mechanics_eb52366033707e1f92bd3d6ea61d29457dbcfa19.png)
We tehn introduce another function of  instead of
instead of  :
:

which gives us
![\begin{equation*}
\Bigg[ \frac{d^2}{d \rho^2} - \frac{\ell (\ell + 1)}{\rho^2} + \frac{2}{\rho} - \lambda^2 \Bigg] u_\ell(\rho) = 0
\label{tise-wrt-u-rho}
\end{equation*}](../../assets/latex/quantum_mechanics_17c59af110e339bfb23ad04579c83ea8ce5fe806.png) 1
1
with boundary conditions:  .
.
We then consider the boundary condition where  :
:
![\begin{equation*}
\rho \to \infty : \Bigg[ \frac{d^2}{d \rho^2} - \lambda^2 \Bigg] u_{\ell}(\rho) = 0 \implies u_{\ell}(\rho) = e^{\pm \rho \lambda}
\end{equation*}](../../assets/latex/quantum_mechanics_bc28652f07b4d56b79761bafdb60a859a5c65c49.png)
But since we need it to be bounded:

Another ansatz:  , which is simply the familiar method of variation of parameters, where we tack on another function of
, which is simply the familiar method of variation of parameters, where we tack on another function of  , the independent variable, to obtain another solution
, the independent variable, to obtain another solution  which is independent of
which is independent of  .
.
If we then plug our  into the [tise-wrt-u-rho], which ends up being
into the [tise-wrt-u-rho], which ends up being
![\begin{equation*}
y_{\ell}''(\rho) - 2 \lambda y_{\ell}' (\rho) + \Bigg[ - \frac{\ell (\ell + 1)}{\rho^2} + \frac{2}{\rho} \Bigg] y_{\ell}(\rho) = 0
\end{equation*}](../../assets/latex/quantum_mechanics_90918c8acb0edf8b06eb95c61ccc0a0429b23e16.png)
where due to the behaviour of  we have
we have

Ansatz:
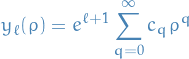
Spin - intrinsic angular momentum
Notation
 denotes the eigenstate of a system with spin (eigenvalue of
denotes the eigenstate of a system with spin (eigenvalue of  )
)  in the z-direction, and
in the z-direction, and  being the eigenvalue of
being the eigenvalue of 
 since the first number (
since the first number ( ) is provided in the second anyways
) is provided in the second anyways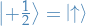 and
and 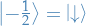
 etc. we use to represent the coefficient of the function
etc. we use to represent the coefficient of the function  in some basis
in some basis- when we say a system has spin
 , we're talking about a system with eigenvalue of
, we're talking about a system with eigenvalue of  to be
to be 
Stuff
Now that we know
![\begin{equation*}
[ \hat{J}_k , \hat{J}_l ] = i \hbar \varepsilon_{klm} \hat{J}_m
\end{equation*}](../../assets/latex/quantum_mechanics_3b516984539a54c7b52c023f4a3520ef48f77318.png)
 eigenvalues:
eigenvalues: 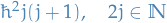
 eigenvalues:
eigenvalues: 
From the orbital angular momentum, we have


In the case of orbital angular momentum , we have the requirement that  , which implies
, which implies  , rather than
, rather than  which we found in the Angular momentum - Reloaded.
which we found in the Angular momentum - Reloaded.
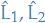 are diff. operators, which implies
are diff. operators, which implies  diff. operators
diff. operators
For a given value of  ,
, 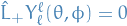 since
since  is the maximum for a spherical harmonic.
is the maximum for a spherical harmonic.

Now using the properties derived for the more general  operator we can deduce the all the other spherical harmonics by the usage of raising and lowering operators.
operator we can deduce the all the other spherical harmonics by the usage of raising and lowering operators.

And it satisfies the commutation relation
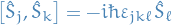
and

Thus, we can construct a basis using the eigenstates of 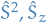 , i.e. they form a C.S.O.C..
, i.e. they form a C.S.O.C..
And as we've seen earlier, if an operator satisfies the above properties, we have:
- eigenvalues of
 :
: 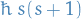 ,
, 
- eigenvalues of
 :
: 
For a given value of  ,
,  has
has  elements
elements

And the eigenfunctions have the relations:
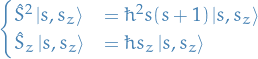
Example: system of spin 1 / 2
Since  , we have:
, we have:
- eigenvalue of
 is
is 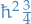
- eigenvalue of
 are
are 
The basis of the space of the physical states is then
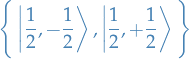
where we use the notation

Thus, any eigenstate we can expand in this basis:
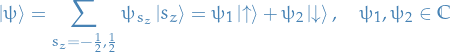
and then
 is the prob. of finding the system in
is the prob. of finding the system in  measuring
measuring 
 is the prob. of finding the system in
is the prob. of finding the system in  measuring
measuring 
TODO Pauli matrices
Since we can write
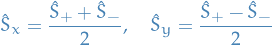
Addition of angular momenta
Notation
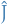 , without integer subscripts refers to the total angular momentum , and thus
, without integer subscripts refers to the total angular momentum , and thus  refers to the z-component of this total angular momentum
refers to the z-component of this total angular momentum refers to the z-component of the angular momentum indexed by, well, 1
refers to the z-component of the angular momentum indexed by, well, 1 refers to the square of the angular momentum indexed by 1
refers to the square of the angular momentum indexed by 1
Stuff
This excerpt from some book might be a really good way of getting a better feel of all of this
In this section we deal with the case of having two angular momenta!
For example, we might wish to consider an electron which has both an intrinsic spin and some orbital angular momentum, as in a real hydrogen atom.
Total angular momentum operator

where we assume  and
and  are independent angular momenta, meaning each satisfies the usual angular momentum commutation relations
are independent angular momenta, meaning each satisfies the usual angular momentum commutation relations

where
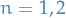 labels the individual angular momenta
labels the individual angular momenta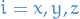 stands for cyclic permutations.
stands for cyclic permutations.
Furthermore, any component of  commutes with any component of
commutes with any component of  :
:
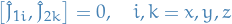
so that the two angular momenta are compatible.
It follows that the four operators  are mutually commuting and thus must posses a common eigenbasis!
are mutually commuting and thus must posses a common eigenbasis!
This common eigenbasis is known as the uncoupled basis and is denoted  .
.
It has the following properties:
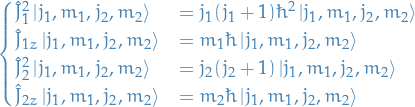
The allowed values of the total angular momentum quantum number  , given two angular momenta corresponding to the quantum numbers
, given two angular momenta corresponding to the quantum numbers  and
and 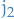 are:
are:
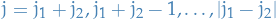
and for each of these values of  , we have
, we have  take on the
take on the  values
values

The z-component of the total angular momentum operator  commutes with
commutes with  and
and  , thus the set of four operators
, thus the set of four operators  are also a mutually commuting set of operators with a common basis known as the coupled basis, denoted
are also a mutually commuting set of operators with a common basis known as the coupled basis, denoted  and satisfying
and satisfying
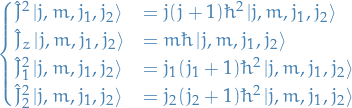
these are states of definite total angular momentum and definite z-component of total angular momentum but not in general states with definite  or
or  .
.
In fact, these states are expressible as linear combinations of the states of the uncoupled basis, with coefficients known as Clebsch-Gordan coefficients.
I think what they mean by "states of definite angular momentum…" are the states which are coupled in a way that one eigenvalue decides the other?
TODO Example: two half-spin particles
Suppose we have two half-spin particles (e.g. electrons) with spin quantum numbers 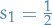 and
and  .
.
According to the Addition theorem, the total spin quantum number  takes on the values
takes on the values 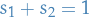 and we require
and we require 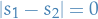 .
.
Thus, two electroncs can only have a total spin:
 called the triplet states, for which there are three possible values of the spin magnetic quantum number
called the triplet states, for which there are three possible values of the spin magnetic quantum number 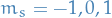
 called the singlet states, for which there are only a single possible value
called the singlet states, for which there are only a single possible value 
Let's denote the elements of the uncoupled basis as

where the subscripts 1 and 2 refer to electron 1 and 2, respectively. The operators  and
and 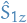 act only on the parts labelled 1, and so on.
act only on the parts labelled 1, and so on.
If we let  be the state which has
be the state which has  and
and 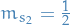 then it must have
then it must have  , i.e. total z-component of spin
, i.e. total z-component of spin  , and can therefore only be
, and can therefore only be  and not
and not  .
.
The eigenstates ends up being:
![\begin{equation*}
\begin{split}
\ket{s = 1, m_s = 1, s_1 = \frac{1}{2}, s_2 = \frac{1}{2}} &= \alpha_1 \alpha_2 \\
\ket{s = 1, m_s = - 1, s_1 = \frac{1}{2}, s_2 = \frac{1}{2}} &= \beta_1 \beta_2 \\
\ket{s = 1, m_s = 0, s_1 = \frac{1}{2}, s_2 = \frac{1}{2}} &= \frac{1}{\sqrt{2}} [ \alpha_1 \beta_2 + \beta_1 \alpha_2 ] \\
\ket{s = 0, m_s = 0, s_1 = \frac{1}{2}, s_2 = \frac{1}{2}} &= \frac{1}{\sqrt{2}} [ \alpha_1 \beta_2 - \beta_1 \alpha_2 ]
\end{split}
\end{equation*}](../../assets/latex/quantum_mechanics_fa572e88aaa427e9656062220ce71e930a158698.png)
Identical Particles
Stuff
Systems of identical particles with integer spin 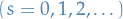 known as bosons , have wave functions which are symmertic under interchange of any pair of particle labels (i.e. swapping the states of say two particles).
known as bosons , have wave functions which are symmertic under interchange of any pair of particle labels (i.e. swapping the states of say two particles).
The wave function is said to obey Bose-Einstein statistics .
Systems of identical particles with half-odd-integer spins 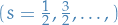 known as fermions , have wave functions which are antisymmetric under interchange of any pair of particle labels.
known as fermions , have wave functions which are antisymmetric under interchange of any pair of particle labels.
The wave function is said to obey Fermi-Dirac statistics .
In the simplest model of the helium atom, the Hamiltonian is
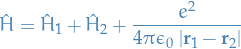
where
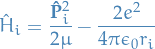
This is symmetric under permutation of the indices 1 and 2 which label the two electrons. Thus it must be the case if the two electrons are identical or industinguishable : it cannot matter which particle we label 1 and we which we label 2.
Due to symmerty condition, we have

Suppose that

so we conclude that  and
and  are both eigenfunctions belonging to the same eigenvalue
are both eigenfunctions belonging to the same eigenvalue  . Further, any linear combination of the two is!
. Further, any linear combination of the two is!
In particular, the normalised symmertic and antisymmertic combinations
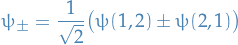
are eigenfunctions belonging to the eigenvalue  .
.
If we introduce the particle interchange operator, 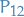 , with the property that
, with the property that

then the symmertic and antisymmertic combinations are eigenfunctions of 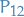 with eigenvalues
with eigenvalues  respectively:
respectively:
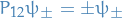
Since  are simultaneous eigenfunctions of
are simultaneous eigenfunctions of  and
and 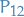 it follows that:
it follows that:
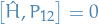
Fourier Transforms and Uncertainty Relations
This is heavily inspired by a post from mathpages.
Notation

 is such that
is such that 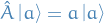 , i.e. the ket corresponding to the eigenvalue
, i.e. the ket corresponding to the eigenvalue 
Stuff
Gaussian integral
- Basic
Taking the square of the integral
 we get
we get
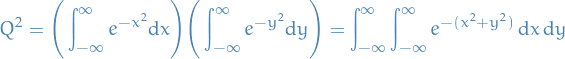
Reparametrizing in polar coordinates

which gives us the Jacobian transformation

so the incremental area element is

Hence the double-integral above becomes
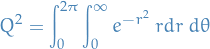
and we since
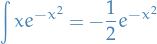
we get
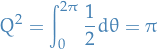
Finally giving us
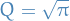
- More general
If we let
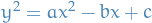 , i.e. we consider some arbitrary quadratic, then
, i.e. we consider some arbitrary quadratic, then

in terms of which we can write
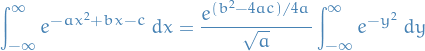
Fourier transform of a normal probability density
For any function  we have the relation
we have the relation
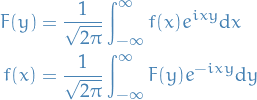
Now, if  is a normal probability density, we have
is a normal probability density, we have
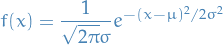
which has the Fourier transform
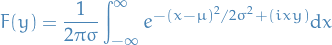
Where we can write the exponent in the integral of the form  with
with
hence the Fourier transform of the normal density function is
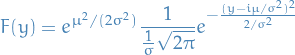
If we then choose our scales so that the mena of  is zero, i.e. so that
is zero, i.e. so that 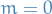 the expression reduces to
the expression reduces to
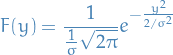
which means that the Fourier transform of a normal distribution with mean  and variance
and variance 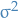 is a normal distribution with mean
is a normal distribution with mean  and variance
and variance  .
.
Which tells us that the variances of the distributions  and
and  satisfy the uncertainty relation:
satisfy the uncertainty relation:

This is the limiting case of the general inequality on the product of variances of Fourier transform pairs. In general, if  is an arbitrary probability density and
is an arbitrary probability density and  is its Fourier Transform, then
is its Fourier Transform, then
For any probability density function  and it's the Fourier Transform
and it's the Fourier Transform  we have
we have

 and
and  are two different ways of characterizing the same distribution, one in the amplitude domain and one in the frequency domain. Given either of these, the other is completely determined.
are two different ways of characterizing the same distribution, one in the amplitude domain and one in the frequency domain. Given either of these, the other is completely determined.
Remember, due to the Central Limit Theorem, i.i.d. the sample mean of any random variable with finite variance follows a Normal distribution
Hence, the equality above is saying that if we have an infinte number of realizations of some random variable  then the variance of this will be bounded below by the inverse of the variance of the Fourier Transform.
then the variance of this will be bounded below by the inverse of the variance of the Fourier Transform.
Hmm, I'm not 100% sure about all this. How can we for sure know that the Fourier Transform of the probability density will have a sample variance which decreases quicker than the actual density function  ?
?
Why can we guarantee that the variance of the Fourier transform does not decrease faster than the variance of the density  ?
?
We're saying that variance of random variable whos sample average converges to  has a variance of
has a variance of  , which is fiiine. Then we're saying that some the variance of some random variable whos sample average converges to
, which is fiiine. Then we're saying that some the variance of some random variable whos sample average converges to  has a variance of
has a variance of  , which is also fine. Then, we're saying that the variance of this random variable is always going to be greater than the limiting variances for these random variables, whiiiich you really can't say.
, which is also fine. Then, we're saying that the variance of this random variable is always going to be greater than the limiting variances for these random variables, whiiiich you really can't say.
Application to Quantum mechanics
The canonical commutation relation is the fundamental relation between canonical conjugate quantities, i.e. quantities which are related by definition such that one is the Fourier transform of the other, which for two operators which are canonical conjugates, we have
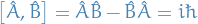
Equivalently, if we have the above commutation relation between two Hermitian operators, then they form a Fourier Transform pair.
Where, if we take the commutation-relation the other way around the the sign of  changes, i.e. it's "symmetric" in a sense.
changes, i.e. it's "symmetric" in a sense.
Now, if we then take some state  and compute the probability amplitudes that the measurements corresponding to the operators
and compute the probability amplitudes that the measurements corresponding to the operators 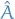 and
and  will return the eigenvalues
will return the eigenvalues  and
and  respectively, then we find
respectively, then we find
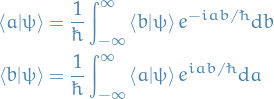
where  is the bra corresponding to the eigenstate
is the bra corresponding to the eigenstate  with the eigenvalue
with the eigenvalue  of the operator
of the operator 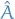 .
.
That is; the probability amplitude distributions of two conjugate variables are simply the (suitably scaled) Fourier transforms of each other.
We saw earlier that the variances of two density distributions that comprise a Fourier transform pair satisfy the variance inequality:

Heisenberg Uncertainty Principle
How is this interesting? Well, as it turns out, the position operator  and the momentum operator
and the momentum operator  have the commutation relation
have the commutation relation

which then tells us that they are conjugate varianbles, i.e. the probability amplitude distributions of the two are scaled Fourier transforms of each other! Which means they satisfy the following inequality

which is just the Heisenberg uncertainty principle!
Bra, kets, and matrices
Time-independent Perturbation Theory
Notation
 is the Hamiltonian corresponding to the unperturbed / exactly solvable system
is the Hamiltonian corresponding to the unperturbed / exactly solvable system and
and  represent the n-th eigenvalue and eigenfunction of the unperturbed Hamiltonian
represent the n-th eigenvalue and eigenfunction of the unperturbed Hamiltonian and
and 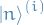 is the energy and ket of the i-th perturbation term
is the energy and ket of the i-th perturbation term and
and  is the corrected (perturbed with all the terms) eigenvalue and eigenfunction, i.e.
is the corrected (perturbed with all the terms) eigenvalue and eigenfunction, i.e.


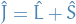 denote the total angular momentum (rather than a general ang. mom. as we've used it for earlier)
denote the total angular momentum (rather than a general ang. mom. as we've used it for earlier)
Overview
- Few problems in Quantum Theory can be solved exactly
- Helium atom: inter-electron electrostatic repulsion term in
 changes the problem into one which cannot be solved analytically
changes the problem into one which cannot be solved analytically
- Helium atom: inter-electron electrostatic repulsion term in
Perturbation Theory provides a method for finding approx. energy eigenvalues and eigenstates for a system whose Hamiltonian is of the form

where
 is the Hamiltonian of an exactly solvable system, for which we know the eigenvalues,
is the Hamiltonian of an exactly solvable system, for which we know the eigenvalues,  , and eigenstates,
, and eigenstates,  , and
, and  is small, time-independent perturbation.
is small, time-independent perturbation.
Does not converge
Perturbation does not actually guarantee convergence, i.e. that each term is smaller than the previous.
But, it is something called Borel summable, which is a method for summing up divergent series.
Short and sweet
Let

where:
 is a real parameter used for convenience
is a real parameter used for convenience is some small perturbation to the Hamiltonian, e.g.
is some small perturbation to the Hamiltonian, e.g. 
Then, the corrected eigenvalues and eigenfunctions are going to be given by:

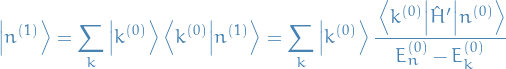
"My" version (first order mainly)
It is convenient to consider the related problem of a system with Hamiltonian

where:
 is a real parameter used for convenience
is a real parameter used for convenience is some small perturbation to the Hamiltonian, e.g.
is some small perturbation to the Hamiltonian, e.g. 
Then the eigenvalue problem we're trying to solve is then:

Assume  and
and  posses discrete, non-degenerate eigenvalues only, and we write:
posses discrete, non-degenerate eigenvalues only, and we write:
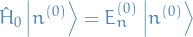
where  are orthonormal.
are orthonormal.
The effect of the perturbation on the eigenstates and eigenvalues is defined by the following maps:
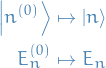
where

Thus, we solve the full eigenvalue problem by assuming we can exapnd  and
and  in a series as follows:
in a series as follows:
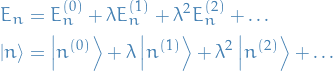
were the correction terms  and
and  are of succesively higher order of "smallness": the power of
are of succesively higher order of "smallness": the power of  keeps track of this for us.
keeps track of this for us.
The correction terms  are not normalized (by defualt)!
are not normalized (by defualt)!
Substitute these into the equation for the full Hamiltonian (can be seen above):
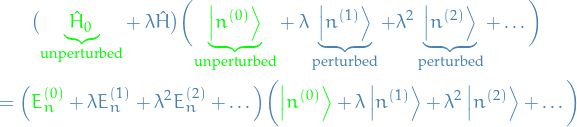
and equating the terms of the same degree of  , giving:
, giving:
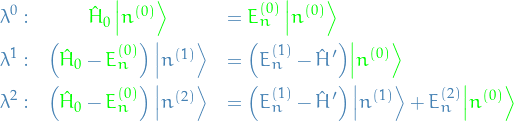
Now let's, for the heck of it, take the inner product of the coefficients of 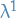 with some arbitrary non-perturbed state
with some arbitrary non-perturbed state  :
:

which (due to  being Hermitian), becomes
being Hermitian), becomes
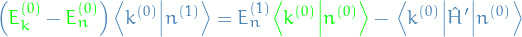
Let's first consider the correction (of first order) to the energy (then we'll to the eigenstate afterwards) by letting 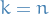 (since
(since  is arbitrary):
is arbitrary):
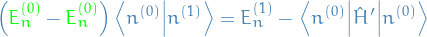
LHS vanishes, and we're left with

which is the expression for the energy correction (of first order)!
To obtain the correction to the eigenfunction itself, we explore the following:  ,
,
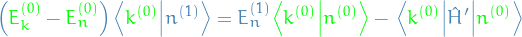
where 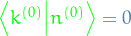 when
when  , thus
, thus
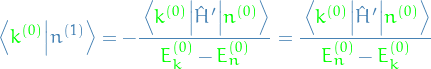
Hence, we can simply expand  in the basis of all
in the basis of all  :
:
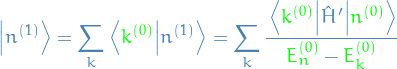
Aaaand we have our expression for the eigenstate correction (of first order)!
Preservation of orthogonality
Let's consider the inner product 
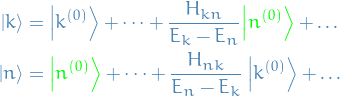
where we've picked out the terms which will be non-zero in  . Observe that the non-zero terms are of different sign, thus
. Observe that the non-zero terms are of different sign, thus
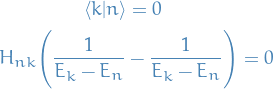
Thus orthogonality is preserved (for first order approximation).
Notes
Corrected
 needs to be normalized, thus we better have
needs to be normalized, thus we better have

- We require that the level shift be small compared to the level spacing in the unperturbed system:
Example: Potential well
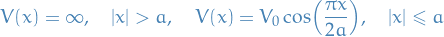
with
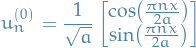
where  ,
,
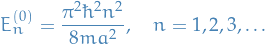
Thus, the first order perturbation correction is
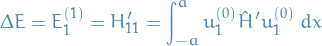

And the second order perturbation correction is
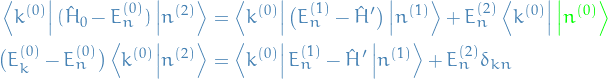
Letting 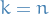 , we have
, we have
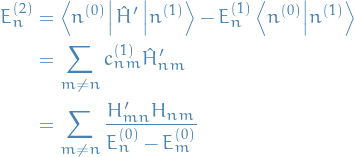
Degeneracy in Perturbation Theory
Notation
- States are ordered s.t. first
 states are degenerate
states are degenerate 


Stuff
Remember, this is the case where  has degenerate eigenstates, and we're assuming that the "real" Hamiltonian
has degenerate eigenstates, and we're assuming that the "real" Hamiltonian  never is degenerate (which is sort of what you'd expect in nature, I guess).
never is degenerate (which is sort of what you'd expect in nature, I guess).
Consider the eigenstate  with degeneracy
with degeneracy 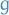 :
:
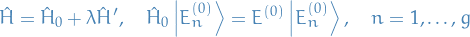
Then
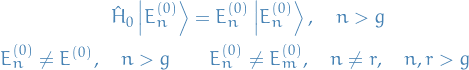
We're just saying that we've ordered the states in such a way that we have state of 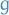 degeneracy occuring in the first
degeneracy occuring in the first 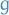 indices.
indices.
Since we have a g-dimensional subspace to work with for the degenerate eigenstate, now, instead of just finding the coefficients as in non-degenerate perturbation theory, we're looking for the "best" linear combination of the eigenbasis for the degenerate case!
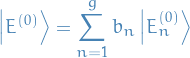
and want to find the "optimal" coefficients / projection.
Proceeding as for the non-degenerate case, we assume that
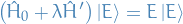
where we assume we can write the following
Substituting the expansions into the eigenvalue equation and equating terms of the same degree  , we find:
, we find:
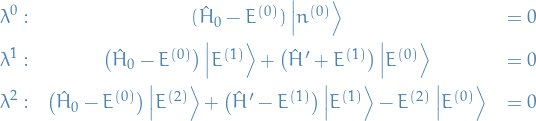
Once again, taking the scalar product with some arbitrary k-th unperturbed eigenstate  , we get
, we get

substituting in
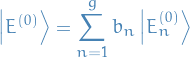
we get
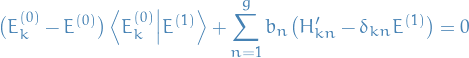
Now we consider the different cases of  .
.
 - degenerate states
- degenerate states
In this case we simply have  and thus the first term vanishes
and thus the first term vanishes
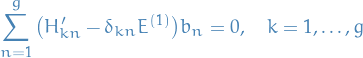
which is simply a "linear algebra eigenvalue problem" (when including for all  )!
)!
We'll denote the "linear algebra eigenvalues" as roots, to distinguish from the eigenvalues from the Schrödinger equation.

where

We get the roots  then have the different cases:
then have the different cases:
 distinct roots => we've broken the degeneracy of
distinct roots => we've broken the degeneracy of  , yey!
, yey!- one or more repeating roots => there's still some degeneracy left from
 , aaargh!
, aaargh! - all equal roots => move on to 2nd order expansion, cuz 1st order didn't help mate!
If we have  distinct roots, we end up with
distinct roots, we end up with

Which is great; it's the same as the non-degenerate case! Therefore, we'd like to arrange for this to always be the case.
Suppose we can find some observable represented by an operator  such that
such that

Then there are simultaneous eigenstates of  and
and 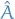 :
:
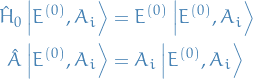
If and only if the eigenvalues 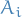 are distinct, then we have a C.S.O.C., and we can write
are distinct, then we have a C.S.O.C., and we can write

Thus,

which is

Therefore,
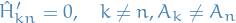
Hence, if  for all
for all  , then
, then  is diagonal, as wanted.
is diagonal, as wanted.
Now, what if  are not distinct?! We then look for another operator
are not distinct?! We then look for another operator  , such that
, such that

i.e. 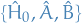 is a C.S.O.C., and letting
is a C.S.O.C., and letting  we can repeat the about argument.
we can repeat the about argument.
We're saying that if we can find some operator which commutes with both  and
and  , we can make
, we can make  diagonalizable, i.e. making our lives super-easy above.
diagonalizable, i.e. making our lives super-easy above.
 - non-degenerate states
- non-degenerate states
We simply take our expansion for  and do exactly what we did for the non-degenerate case!
and do exactly what we did for the non-degenerate case!
Example
Central potential, spin-(1/2), spin-orbit interaction:
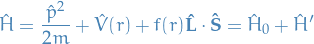
We know that

so if we use the coupled basis 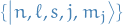 , we can use the non-degeneracy theory to compute the 1st order energy shifts!
, we can use the non-degeneracy theory to compute the 1st order energy shifts!

but

because of the  term in
term in  .
.
Example: Hydrogen fine structure
Notation
 denotes the spin-orbit term, whose physical origin is the interaction between the intrinstic magnetic dipole moment of the electron and the magnetic field due to the electron's orbital motion in the electric field of the nuclues
denotes the spin-orbit term, whose physical origin is the interaction between the intrinstic magnetic dipole moment of the electron and the magnetic field due to the electron's orbital motion in the electric field of the nuclues
Stuff

with

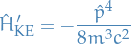
We start with the kinetic energy
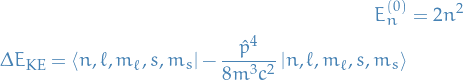
Where
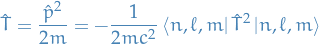
Therefore

Which appearantly give us
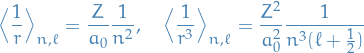
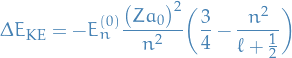
And for the spin-orbit interaction we have


which gives us
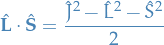
Applying this to some ket
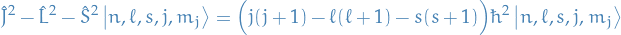
Thus,
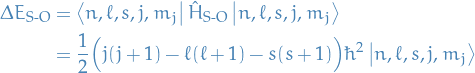
where
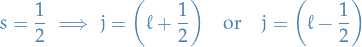
thus, if

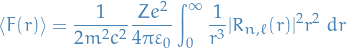
Which gives us
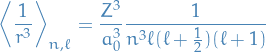
implying

And finally for the Darwin-correction
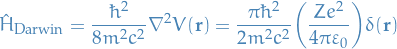
Observe that  as
as  for
for  , then
, then

where
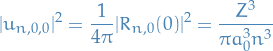
Which gives us the final Darwin correction
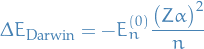
Giving the total correction
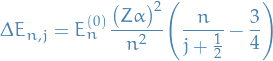
Example: Helium atom
Notation
 represents the spin-down state
represents the spin-down state represents the spin-up state
represents the spin-up state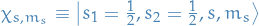 is the states for the coupled basis, where
is the states for the coupled basis, where  is the total spin quantum number and
is the total spin quantum number and  is the total magnetic quantum number
is the total magnetic quantum number
Neglecting mutual Coulomb repulsion between the electrons
Neglecting the mututal Coulomb repulsion between the electrons we end up with the Hamiltonian

It turns out that this yields the ground-state energy just
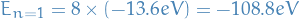
but experimentally we find

For the Helium atom we use the convention of denoting the ground state with 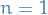 rather than
rather than 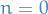 as for the Hydrogen atom.
as for the Hydrogen atom.
Stuff
In the simplest model of the helium atom, the Hamiltonian is
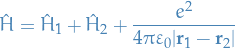
where
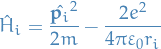
The term added to  represents the repulsion of the two electrons, and in the
represents the repulsion of the two electrons, and in the  we have the negative term which represents the attraction.
we have the negative term which represents the attraction.
Also, observe that this is symmertic under permutation of the indices which label the two electrons. Thus, the electrons are indistinguishable, as one would want.
The states of the coupled representation for the two spin-half electrons are the three triplet states:
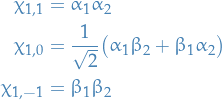
and the singlet state:
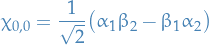
- triplet states are symmetric under permutation
- singlet state is anti-symmetric under permutation
The overall 2-electron wavefunction is a product of a spatial wavefunction and a spin function:

The tensor product between the spatial wavefunction, 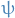 , and the spin function,
, and the spin function,  , represents some function
, represents some function  such that
such that

where  is as defined above.
is as defined above.
Thus, the total 2-electron wavefunction has the following symmetries:
symmetry of 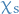 |
symmetry of 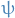 |
symmerty of  |
|
|---|---|---|---|
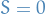 (singlet) (singlet) |
anti | sym | anti |
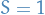 (triplet) (triplet) |
sym | anti | anti |
Consider the case of the Helium atom, where (if we're neglecting the inter-electron interactions) we would have the spatial solutions

since we can just use separation of variables and solve the Schrödinger eqn. for each electron separately, both having identical solutions.
Now, suppose further that 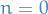 , and thus
, and thus 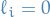 and
and  , then
, then

Now consider the case where they would swap places, i.e. we were to interchange them (we're assuming they're completely opposite to each other, since i 2-electron orbit, they're almost always opposite of each other), then

Now, we know that

Therefore,  , as we have above, is symmetric:
, as we have above, is symmetric:

Thus,

BUT we know that two fermions cannot occupy the same state at the same time, hence the above is not sufficient! We need the wave-functions to be different, further, for the wave-function of the entire Helium to stay the same we require the wave-functions to be anti-symmetric under interchanging of electrons (for  , that is). And this is why we introduce the
, that is). And this is why we introduce the  described earlier
described earlier
Ground state

Compute the first order correction to  , we compute the expectation of the perturbation
, we compute the expectation of the perturbation  , wrt. wavefunction:
, wrt. wavefunction:

which gives us a correction of
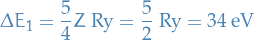
giving us the first order estimate of the ground-state energy

which is pretty close to the experimentally observed value of  .
.
Stuff
Define a new operator

With

Then we want to expand wrt. 
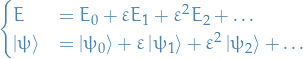
Setting up the Schrödinger equation, we have
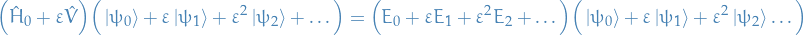
Now, collecting terms involving the different factors of  , we have:
, we have:
For
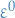 we find:
we find:

and therefore
 has to be one of the unperturbed eigenfunctions
has to be one of the unperturbed eigenfunctions  and
and  , i.e. the corresponding unperturbed eigenvalue.
, i.e. the corresponding unperturbed eigenvalue.
For
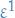 we have:
we have:
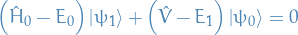
Which we can take the scalar product of with
 :
:

Since
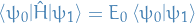 , we have
, we have

Hence, the eigenvalue of the Hamitonian in this case becomes:
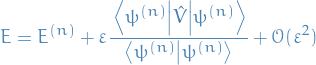
This is the correction to the n-th energy level! So to obtain the complete correction due to the perturbation, we have to do this for each of the eigenfunctions which make up the wave-function of the entire system we're looking at.
He atom

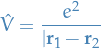


Time-dependent Perturbation Theory
Notation
 is the Hamiltonian corresponding to the unperturbed / exactly solvable system
is the Hamiltonian corresponding to the unperturbed / exactly solvable system and
and  represent the n-th eigenvalue and eigenfunction of the unperturbed Hamiltonian
represent the n-th eigenvalue and eigenfunction of the unperturbed Hamiltonian and
and 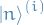 is the energy and ket of the i-th perturbation term
is the energy and ket of the i-th perturbation term and
and  is the corrected (perturbed with all the terms) eigenvalue and eigenfunction, i.e.
is the corrected (perturbed with all the terms) eigenvalue and eigenfunction, i.e.

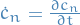

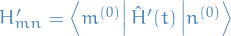
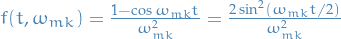
 is the density of final states
is the density of final states
Expression for 
Solution to the TIDE can be written
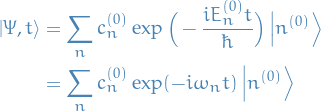
Generalize to the perturbed Hamiltonian

the coefficients
 become time-dependent:
become time-dependent:

Observe that lack of  here!!!
here!!!
We're not yet using the perturbation here, which would be

This is comes in the next section.
Probability of finding the system in the state
 at time
at time  is then
is then
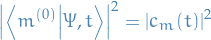
where we have used the orthonormality of
 .
.
Substituting into TDSE:
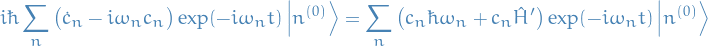
which gives:

Taking scalar product with arbitrary unperturbed state
 :
:

which gives:

Perturbation
Now consider the Hamiltonian related to the perturbed one above:

Assume we can expand
 in power series:
in power series:
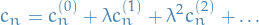
Substitute in the equation for
 derived above (factor of
derived above (factor of  on RHS is from
on RHS is from  now instead of
now instead of  ):
):

Equate terms of same degree in
 :
:
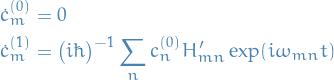
- Zeroth order is time-independent; since to this order the Hamiltonian is time-independent => recover unperturbed result
Integrating first-order correction gives:

Suppose initially system is eigenstate of
 , say
, say  , then for
, then for  , /probability of finding system in different state
, /probability of finding system in different state  at time
at time 

Thus, transition probability of finding the system at a later time,
 , in the state
, in the state  where
where  , is given by
, is given by
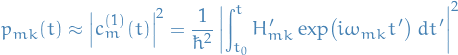
TODO Time-independent pertubations for time-dependent wave equation
- Suppose
 is actually independent of time
is actually independent of time
Fermi's Golden Rule
Interested in transitions not to single state, but to a group of final states,
 , in some range:
, in some range:

e.g. transitions to continuous part of energy-spectrum.
Total transition probability:
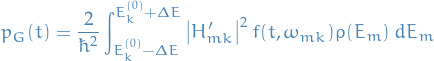
Assume
 to be small, s.t. can treat
to be small, s.t. can treat  constant wrt.
constant wrt.  on this interval:
on this interval:

Change of variables
 , we get
, we get
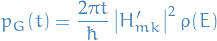
where we've used

Number of transitions per time, the transition rate,  , is then just
, is then just

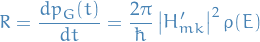
Harmonic Perturbations
Notation
 is the time-independent Hermitian operator
is the time-independent Hermitian operator
Stuff
- Transition probability amplitude is a sinusoidal function of itme which is turned on at time

Suppose that

where
 is the time-independent Hermitian operator, which we write
is the time-independent Hermitian operator, which we write
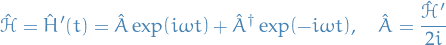
Radiation
Notation
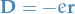 is the dipole operator
is the dipole operator
Electromagnetic radiation
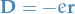 is the dipole operator where
is the dipole operator where
 is unit charge
is unit charge
Einstein A-B coefficients
Notation
 is the absorption rate
is the absorption rate is the emission rate
is the emission rate Einstein coeff. for spontanous emission
Einstein coeff. for spontanous emission Einstein coef. for stimulated emission
Einstein coef. for stimulated emission dipole matrix elements
dipole matrix elements
Spontanoues emission (thermodynamic argument)
We have
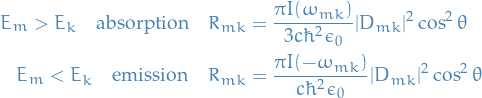
For absorption we have
![\begin{equation*}
\begin{split}
\dot{N}_{mk} &= N_k \rho(\omega_{mk}) B_{mk} \\
\dot{N}_{mk} &= R_{mk] N_k \\
B_{mk} &= \frac{R_{mk}}{\rho(\omega_{mk})} c \frac{R_{mk}}{I(\omega_{mk}}} \\
\implies B_{mk} & = \frac{\pi}{3 \hbar^2 \epsilon_0} |D_{mk}|^2
\end{split}
\end{equation*}](../../assets/latex/quantum_mechanics_a4141c89b669d5aacc3b6ecd2195364fb6559e66.png)
Now, suppose we have emission , with transition  :
:

Note that this is  , NOT
, NOT  as introduced earlier.
as introduced earlier.
The distribution between the number of particles in the different states is then given by the Boltzmann distribution
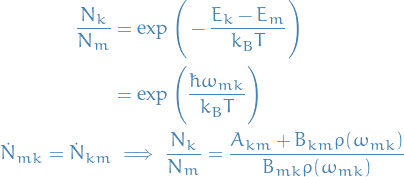
Plank's law tells us that Black body radiation follows
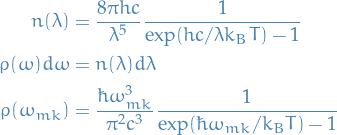
Which we can rewrite as
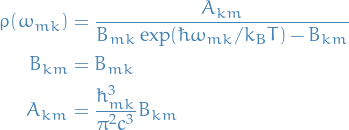
Substituting back into the epxression for spontaneous emission
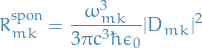
One obtains the same result in QED.
Selection rules
Goal is to evaluate  .
.
Hydrogenic atom
- electric dipole operator is spin-independent
- work in uncoupled basis and ignore spin
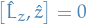
Which implies
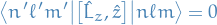
Which implies either of the following is true
This is called a selection rule.
Doing the same for  , we get
, we get

Considering the matrix elements, we get

which becomes

so we deduce that

giving the selection rule 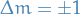 .
.
We then conclude that the electric dipole transitions are only possible if

Which is due to
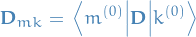
hence  would be zero unless
would be zero unless  .
.
Parity Selection Rule
- Under parity operator
 , electric dipole operator is odd multi-electron atoms
, electric dipole operator is odd multi-electron atoms - See notes :)
Quantum Scattering Theory
Notation
 is the scattering angle
is the scattering angle is the incident angle
is the incident angle is the incident momentum
is the incident momentum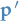 is the scattering momentum (i.e. momentum after being scattered)
is the scattering momentum (i.e. momentum after being scattered) , thus when we talk about the direction and so on of
, thus when we talk about the direction and so on of  (wave-number), it's equivalent to the angle of the momentum
(wave-number), it's equivalent to the angle of the momentum is the solid angle
is the solid angleRate of transitions from initial to final plane-wave states

 is the density of the final states:
is the density of the final states:  is the number of final states with energy in the range
is the number of final states with energy in the range 
 denotes fixed potential (i.e. we say the "potential source" is fixed at some point and
denotes fixed potential (i.e. we say the "potential source" is fixed at some point and  is then the position of the incident particle, and we treat the potential from the fixed scattering-particle as a regular "external" field)
is then the position of the incident particle, and we treat the potential from the fixed scattering-particle as a regular "external" field)
Setup
- Beam of particles
- Each of momentum

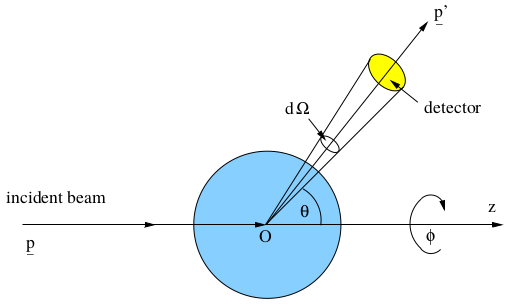
The incident flux is the number of incident particles crossing unit area perpendicular to the beam direcion per unit time.
The scattered flux is the number of scattered particles scattered into the element of solid angle  about the direction
about the direction  ,
,  perunit time per unit solid angle.
perunit time per unit solid angle.
The differential cross-section is usually denoted  and is defined to be the ratio of the scattered flux to the incident flux:
and is defined to be the ratio of the scattered flux to the incident flux:

The differential cross-section thus has dimensions of area: ![$[L]^2$](../../assets/latex/quantum_mechanics_30b4b5cb961eecc96c323ceea58d701ae12b25ef.png)
Total cross-section is then
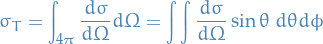
Born approximation
- Can use time-dependent perturbation teory theto approximate the cross-section
- Assume interaction between particle and scattering centre is localized to the region around

Hamiltonian

and treat
 as perturbation
as perturbation
- Wave-functions are non-normalizable, therefore we restrict to "potential-well" scenario, as we can take the width of the well as large as we "want"
- Since we're working in 3D: box-normalization
Density of final states
- Final-state vector
 is a point in k-space
is a point in k-space - All
 form a cubic lattice with lattice spacing
form a cubic lattice with lattice spacing  (because of the potential well approx. discretizing the energy)
(because of the potential well approx. discretizing the energy) - Volume of k'-sphere per lattice point is
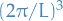
# of states in volume element
 is
is
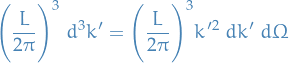
using spherical coordinates
Energy is
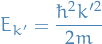
thus, the
 , the density of states per unit energy, is the enrgy corresponding to wave-vector
, the density of states per unit energy, is the enrgy corresponding to wave-vector  . Therefore,
. Therefore,
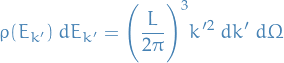
is the # of states with energy in the desried interval and with
 pointing into the solid angle
pointing into the solid angle  about the direction
about the direction  .
.
Final result for density of states
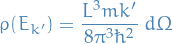
Incident flux
Box normalization corresponds to one particle per volume

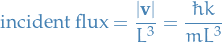
Scattered flux
-
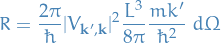
- Is # of particles scattered into
 per unit time
per unit time - Scattered flux therefore obtained by dividing by
 to get # of unit time per unit solid angle
to get # of unit time per unit solid angle
Differential Cross-section for Elastic Scattering
Can compute the cross-section using scattered flux and incident flux found earlier
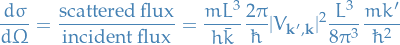
If potential is real, energy conservation implies elastic scattering, i.e.
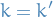
The Born approximation to the differential cross-section then becomes
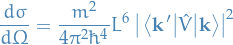
with
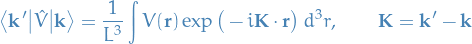
where  is called the wave-vector transfer.
is called the wave-vector transfer.
(this is just the 3-dimensional Fourier transform of the potential energy function.)
Scattering by Central potentials
- Can simplify further
Work in polar coordinates
 , which refer to the wave-vector transfer
, which refer to the wave-vector transfer  so that
so that
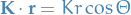
Then
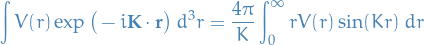
Born approximation then becomes
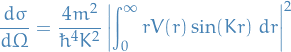
which is independent of
 but depends on the scattering angle,
but depends on the scattering angle,  , through
, through  .
.
Trigonometry gives

Quantum Rotator
- Two particles of mass
 and
and  separated by fixed distance
separated by fixed distance 
- Effective description of the rotational degrees of freedom of a diatomic molecule
- Choose centre-of-mass as origin: system is completely specified by angles
 and
and  (since
(since  is fixed)
is fixed) - Neglecting vibrational degrees of freedom, both
 and
and  are constant, and
are constant, and 
Since origin is frame of CM:
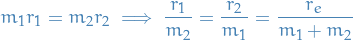
(Classically) Moment of intertia of the system is:

where
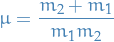
Classical mechanics:

where
 is the angular velocity of the system. The energy can be expressed as
is the angular velocity of the system. The energy can be expressed as
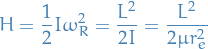
Correspondance principle:
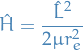
Since we're neglecting vibration,
 is fixed, hence the wave function is independent of
is fixed, hence the wave function is independent of  :
:
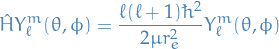
Two-body scattering
- So far assumed beam of particle scattered by fixed scattering centre; interaction described by

- Useful for electron-atom scattering due to regarding the atom as infinitively heavy
- Consider two-particle system; turns out it's the same!
Hamiltonian with relative separation
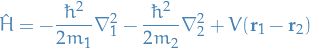
Centre of mass and relative position vectors
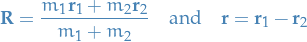
Then

Rewrite gradient operators
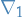 and
and  by
by
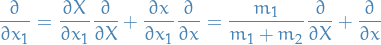
where

and so on.
To see this just apply the differential operator wrt.  to some function
to some function  :
:
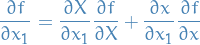
Then
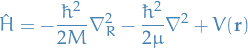
where

with
 called the reduced mass
called the reduced mass
Can be viewed as

 describes free motation (kinetic energy) of centre of mass
describes free motation (kinetic energy) of centre of massIn CM frame the CM is at rest, hence
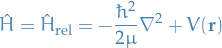
which is identical to the form of Hamiltonian of a single particle moving in the fixed potential

- Implies CM cross-section for two-body scattering obtained from solution to single particle of mass
 scattering from fixed potential
scattering from fixed potential
 Ion and Bonding
Ion and Bonding
Notation
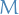 is the mass of a proton
is the mass of a proton is the mass of an electron
is the mass of an electron reduced mass of the electron/two-proton system
reduced mass of the electron/two-proton system
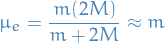
 is the reduced mass of the two-proton system
is the reduced mass of the two-proton system
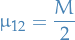
- eigenfunction is called gerade if parity is even, and ungerade if the parity is odd
Stuff
Schrödinger equation is
![\begin{equation*}
\Bigg[ - \frac{\hbar^2}{2 \mu_{12}} \nabla_R^2 - \frac{\hbar^2}{2 \mu_e} \nabla_r^2 - \frac{e^2}{(4 \pi \epsilon_0) r_1} - \frac{e^2 }{(4 \pi \epsilon) r_2} + \frac{e^2}{(4 \pi \epsilon_0) R} \Bigg] \psi(\mathbf{r}, \mathbf{R}) = E \psi(\mathbf{r}, \mathbf{R})
\end{equation*}](../../assets/latex/quantum_mechanics_844fc9792e787f53554a49a0ccbf6973c7a88b11.png)
- Nuclei massive compared to electrons, thus motion of nuclei much slower than electron
- Therefore, treat nuclear and electronic motions independently, further treat the nuclei as fixed, i.e. we only care about
Central Field Approximation
Notation
 is angular momentum quantum number
is angular momentum quantum number is magnetic quantum number
is magnetic quantum number is mass
is mass
Stuff
Starting with the TISE, we have:
![\begin{equation*}
\Bigg[ - \frac{\hbar^2}{2 \mu} \nabla^2 + V(r) \Bigg] u(\mathbf{r}) = E u(\mathbf{r})
\end{equation*}](../../assets/latex/quantum_mechanics_13bbbaed0b51bcbaa3c90d5ffd6342c6a32f24fc.png)
Rewriting in spherical coordinates, using the Laplacian in spherical coordinates and assuming

we have
![\begin{equation*}
\frac{\hbar^2}{2 \mu} \Bigg[ - \frac{1}{r^2} \frac{\partial}{\partial r} \bigg( r^2 \frac{\partial}{\partial r} \bigg) + \frac{1}{\hbar^2 r^2}\hat{L}^2 \Bigg] R(r) Y_{\ell}^m(\theta, \hpi) = \Big( E - V(r) \Big) R(r) Y_{\ell}^m(\theta, \phi)
\end{equation*}](../../assets/latex/quantum_mechanics_aff636d3c57d7a5a6ce07c5046ce69e4177d6a52.png)
which becomes:
![\begin{equation*}
\frac{1}{r^2} \frac{d}{dr} \Bigg( r^2 \frac{dR}{dr} \Bigg) - \frac{\ell (\ell + 1)}{r^2} R + \frac{2 \mu}{\hbar^2} \big[ E - V(r) \big] R = 0
\end{equation*}](../../assets/latex/quantum_mechanics_5ccf61ee8b9b365e46864854a5927d29ebb4f5e7.png)
Suppose
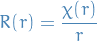
then the above equation becomes
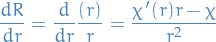
Thus,
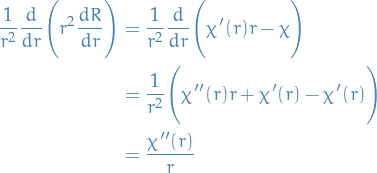
Substituting back into the equation we just arrived at, we obtain
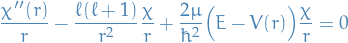
Multiplying by 
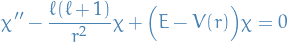
Which we can rewrite as
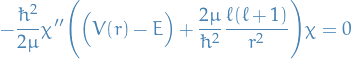
Therefore we consider this is a effective potential:
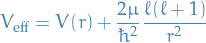
Example: charged nucleus
Consider the problem of an atom or ion containing a nucleus withcharge  and
and  elecrons.
elecrons.
We assume nucleus to be infinitively heavy and we assume only the following interactions are present:
- Coulomb interaction between each electron and the nucleus
- Mutual electronic repulsion
Then the Hamiltonian is
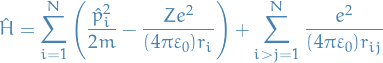
Presence of electron-electron interaction terms (2nd sum) means that the Schödinger equation is not separable.
Therefore we introduce the Central Field Approximation, which is an example of a independent particle model , in which we assume that each electron moves in an effective potential  , which incorporates the nuclear attraction and the average effect of the repuslive interaction with the other
, which incorporates the nuclear attraction and the average effect of the repuslive interaction with the other  electrons.
electrons.
We expect this effective potential to have the following properties:
![\begin{equation*}
\lim_{r \to 0} V_{\text{eff}}(r) = - \frac{Ze^2}{(4 \pi \varepsilon_0) r} \quad \text{and} \quad \lim_{r \to \infty} V_{\text{eff}}(r) = - \frac{[Z - (N - 1)]^2 e^2}{(4 \pi \varepsilon_0) r}
\end{equation*}](../../assets/latex/quantum_mechanics_f794bd063ae01f789bbf88a2c1adf21aa00eca22.png)
 means the nucleus dominates
means the nucleus dominates means that we can treat (nuclues) + (the rest of the electrons) as a point-charge
means that we can treat (nuclues) + (the rest of the electrons) as a point-charge
Variational Method
- Especially useful for estimating the ground-state energy of a system
- This is closesly (if not "exactly") related to the Rayleigh quotient from Linear algebra
Main problem is guessing a trial function  :
:
- Recognize properties of the system and observe that
 ought to have the same properties (e.g. symmetry, etc.)
ought to have the same properties (e.g. symmetry, etc.)
Useful identity:
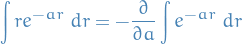
Consider a system described by a Hamiltonian  , with a complete orthonormal set of eigenstates
, with a complete orthonormal set of eigenstates  and corresponding energy eigenvalues
and corresponding energy eigenvalues  ordered in increasing value
ordered in increasing value

We observe that

since  for all
for all  . Thus we have the inequality
. Thus we have the inequality

Thus, we can estimate  as follows:
as follows:
- We chose a trial state
 which depends on one or more paramters
which depends on one or more paramters  .
. Calculate
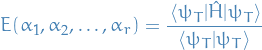
Minimize
 wrt. the variational parameters
wrt. the variational parameters  , by solving
, by solving
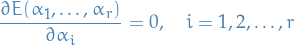
The resulting minimum value of  is then our best estimate for the ground-state energy of the given trial function.
is then our best estimate for the ground-state energy of the given trial function.
Hidden Variables, EPR Paradox, Bell's Inequality
- Hidden variable theories suppose that there exist parameters which fully determine the values of the observables, and that QM is an incomplete theory where the wavefunction simply reflects the probability distribution wrt. to these parameters
EPR though experiment
- Two measuring devices (Alice and Bob)
- Electron sent from the middle where due to conservation of momentum (total spin
 needs to be conserved) we need:
needs to be conserved) we need:
- Alice to receive
 or
or 
- Bob receives the state which Alice does not
- Alice to receive
- Distance between measuring devices is too large to exchange any information between the the two measuring devices (even at speed of light)
Consider the following cases:
- Both measures spin-state in z-direction: measuring Alice's completely determines what we measures at Bob, due to spin being conserved
- Alice measures along z-direction, Bob measures along x-direction: measuring Alice's does not completely determine Bob's measure, rather, both spin-half states will be equally likely for Bob
The state of the "electron" measured by Bob will be correlated to the direction in which Alice makes the measurement!
Bell's Inequality
Notation
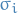 spin component in direction
spin component in direction  of the particle travelling to
of the particle travelling to  , e.g.
, e.g.  refers to taking on a specific configuration (remember we can only measure one of these directions)
refers to taking on a specific configuration (remember we can only measure one of these directions) spin component in direction
spin component in direction  of the particle travelling to
of the particle travelling to 
 is the fraction of particle-pairs belong to the group
is the fraction of particle-pairs belong to the group 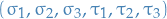
 denotes the probability of measuring
denotes the probability of measuring 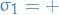 and
and 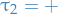 together
together
Stuff
Since we're assuming that the spin-half pair is produced in a singlet state, this tells us immediately that

Suppose then that we're measuring  and
and  , we marginalize out all the other possible states to obtain the distribution:
, we marginalize out all the other possible states to obtain the distribution:

Observe that
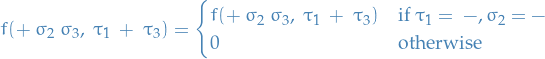
Thus,
Doing the same for the pairs  and
and  we observe that
we observe that
The Bell's Inequality is for measurements made of two spin-half particles in directions  :
:

which defines a requirement which needs to be satisfied for a theory to be a realistic local theory.
Components possessing objective properties which exist independently of any mesaurements by observers and that the result of a measurement of a property at point  cannot depend on an event at point
cannot depend on an event at point  sufficiently far from
sufficiently far from  that information about the event at
that information about the event at  , even travelling at the speed of light, could not reach
, even travelling at the speed of light, could not reach  until after the measurement has taken place.
until after the measurement has taken place.
Theories meeting these requiremenets are called realistic local theories.
Quantum communication
Notation
 , i.e. these all denote the same thing
, i.e. these all denote the same thingConvention to represent these two states
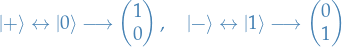
which is often parametrized in polar angles
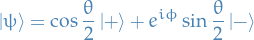
with
![$\theta \in [0, \pi]$](../../assets/latex/quantum_mechanics_5c3c0e9ea23efc5b0a5dbe637fa9ffdc48a38e69.png) and
and ![$\phi \in [0, 2 \pi]$](../../assets/latex/quantum_mechanics_79aa086b78e7b08c1293c05ca0ccc25029aeabc4.png) .
.
Bell's states:
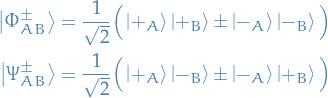
Secure communication
An entangled state between systems  and
and  implies the wavefunction of the combined
implies the wavefunction of the combined  and
and  systems cannot be written as a tensor-product of independent wavefunctions for each system, i.e.
systems cannot be written as a tensor-product of independent wavefunctions for each system, i.e.

The Bloch sphere is just the parametrization of a two-qubit system in polar angles in 3d:
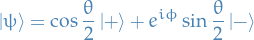
with ![$\theta \in [0, \pi]$](../../assets/latex/quantum_mechanics_5c3c0e9ea23efc5b0a5dbe637fa9ffdc48a38e69.png) and
and ![$\phi \in [0, 2 \pi]$](../../assets/latex/quantum_mechanics_79aa086b78e7b08c1293c05ca0ccc25029aeabc4.png) .
.
A frequently used complete set of two-qubit states in which both qubits are entangled, are the Bell states,
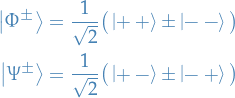
No-cloning theorem
It is impossible to create an identical copy of an arbitrary unknown quantum state.
Formally, let  where
where  denotes a Hilbert space.
denotes a Hilbert space.
Suppose we're in some initial state  , then initially we have
, then initially we have

Then the question is: can we turn  into a duplicate state of
into a duplicate state of  ?
?
- Observing
 will collapse the state, thus corrupting the state we want to copy
will collapse the state, thus corrupting the state we want to copy - Can control
 of the system and evolve
of the system and evolve  with unitary time evolution operator
with unitary time evolution operator  ,
where by unitary operator we mean that it preserves the norm and coherence.
,
where by unitary operator we mean that it preserves the norm and coherence.
Answer is no.
Suppose  on
on  such that
such that
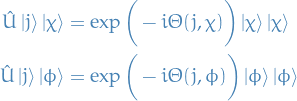
where  and
and  are two arbitrary states in
are two arbitrary states in  .
.
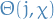 is the angle which in general can be a function of the states on which
is the angle which in general can be a function of the states on which  is acting. Then we have
is acting. Then we have
![\begin{equation*}
\begin{split}
\bra{\chi}\ket{\psi} = \bra{\chi} \bra{j} \hat{U}^\dagger \hat{U} \ket{j} \ket{\psi} &= \exp \big[ i \big( - \Theta(j, \phi) + \Theta(j, \chi) \big) \big] \bra{\chi} \bra{\chi}\ket{\phi} \ket{\phi} \\
&= \exp \big[ i \big( - \Theta(j, \phi) + \Theta(j, \chi) \big) \big] \bra{\chi}\ket{\phi}^2
\end{split}
\end{equation*}](../../assets/latex/quantum_mechanics_457a20254f7bca6ad3b4988aef0e4bec70348d76.png)
This equation leads to the condition
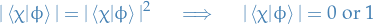
I.e. states are either orthogonal or the same.
Quantum teleportation of a qubit
Two spin-half particles are prepared in the Bell state
![\begin{equation*}
\ket{\Psi_{AB}^-} = \frac{1}{\sqrt{2}} \Big[ \ket{+_A} \ket{-_B} - \ket{-_A} \ket{+_B} \Big]
\end{equation*}](../../assets/latex/quantum_mechanics_2407d9c5e7146a89e6175e268f43d42ee7d8079b.png)
- Establish a quantum channel by giving one of the electrons to Alice (
 ) and one to Bob (
) and one to Bob ( ); due to the EPR-stuffs we know that if Alice makes a measurement, she can use a classicial channel to tell Bob which state she measured, which tells Bob that his electron is in the opposite state.
); due to the EPR-stuffs we know that if Alice makes a measurement, she can use a classicial channel to tell Bob which state she measured, which tells Bob that his electron is in the opposite state. New particle given to Alice (Bob also knows that
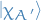 also takes this form)
also takes this form)

Combine with the EPR states (referring to the ones Alice and Bob received beforehand)
![\begin{equation*}
\begin{split}
\ket{\Phi_{A' A B}} &= \frac{c}{\sqrt{2}} \ket{+_{A'}} \ket{\Psi_{AB}^-} + \frac{d}{\sqrt{2}} \ket{-_{A'}} \ket{\Psi_{AB}^-} \\
&= \frac{c}{2} \Big[ \ket{+_{A'}} \ket{+_A} \ket{-_B} - \ket{ +_{A'}} \ket{-_A} \ket{ +_B } \Big] \\
& \ + \frac{d}{2} \Big[ \ket{-_{A'}} \ket{+_{A}} \ket{-_B} - \ket{-_{A'}} \ket{-_A} \ket{+_B} \Big]
\end{split}
\end{equation*}](../../assets/latex/quantum_mechanics_27038b9c0ddef1cac90ff9f1c11285afa2d02f9f.png)
which we can rewrite in terms of the Bell-basis:
![\begin{equation*}
\begin{split}
\ket{\Phi_{A' A B}} =& \frac{1}{2} \Big[ \ket{\Psi_{A' A}^-} \big( - c \ket{ +_B} - d \ket{ -_B} \big) \\
& + \ket{\Psi_{A' A}^+ } \big( - c \ket{+_B} + d \ket{-_B} \big) \\
& + \ket{\Phi_{A' A}^-} \big( c \ket{-_B} + d \ket{+_B} \big) \\
& + \ket{\Phi_{A' A}^+} \big( c \ket{-_B} - d \ket{+_B} \big) \Big]
\end{split}
\end{equation*}](../../assets/latex/quantum_mechanics_9afc91f14d66f9c5aa646aaab2d542f917846982.png)
- Alice makes measurement of the two-state system consisting of
 and
and 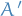 (this can in fact be performed physically)
(this can in fact be performed physically)
- Collapses
 to one of the
to one of the  or
or 
- Alice now knows which of the states
 or
or  her system is in
her system is in Breaks entanglement with
 and forces
and forces  to take on the "remainder" of the system, i.e. one of the
to take on the "remainder" of the system, i.e. one of the

- Collapses
- Alice sends back to Bob which state
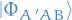 collapsed to
collapsed to
- Since Bob knew the expression for
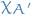 , by learning which state
, by learning which state 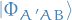 is in, he can fully determine what state his own particle is in, i.e. the coefficient of
is in, he can fully determine what state his own particle is in, i.e. the coefficient of  and
and 
- This tells Bob which transformation he needs to perform to get his own particle into the state which
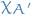 was originally in!
was originally in!
- Since Bob knew the expression for
Superdense coding
Superdense coding is a procedure that utilises an entangled state between two participants in a way that one participant can transmit two bits of information through the act of sending over just one qubit.
Q & A
DONE Is there a correspondance between "unitary transformation / operator" and unitary matrices (when representing the operator as a matrix)?
Check out the definition of a
TODO Not quite sure about how representations used in the Superdense coding step-by-step procedure in the notes
Quantum computing
A quantum register is simply the entire state vector.
Usually we write it in the following form:

where:
 are called control or input register (does not necessarily make sense, it's just a term)
are called control or input register (does not necessarily make sense, it's just a term) are called the target or output register (does not necessarily make sense, it's just a term)
are called the target or output register (does not necessarily make sense, it's just a term) and
and  are states labelled by
are states labelled by  and
and  bits
bits
Example:  is a control ket specified by a binary number of length 2, i.e. a linear combination of the states
is a control ket specified by a binary number of length 2, i.e. a linear combination of the states  ,
,  ,
,  , and
, and  .
.
Algorithms
Notation
 is called the oracle
is called the oracleQuantum register :

Deutch's algorithm
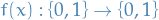
And we're wondering


 is working in
is working in 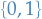 , thus
, thus
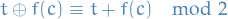

where
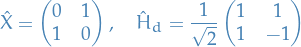
and

Applying the operator above, we get
![\begin{equation*}
\begin{split}
& \frac{1}{2 \sqrt{2}} \ket{0} \Big[ \ket{f_i(0)} - \ket{1 + f_i(0)} - \ket{f_i(1)} + \ket{1 + f_i(1)} \Big] \\
+ & \frac{1}{2 \sqrt{2}} \ket{1} \Big[ \ket{f_i(0)} - \ket{1 + f_i(0)} + \ket{f_i(1)} - \ket{1 + f_i(1)} \Big]
\end{split}
\end{equation*}](../../assets/latex/quantum_mechanics_abfa29fdca93df592b3e273419508009cf6eaa9b.png)
Thus, for  this leads to
this leads to
![\begin{equation*}
\frac{1}{2} \ket{0} \Big[ \ket{f_i(0)} - \ket{1 + f_i(0)} \Big]
\end{equation*}](../../assets/latex/quantum_mechanics_e3b21c1942e1b7f3c2f5e40c6d382c1fd2bd1703.png)
and for  , we have
, we have
![\begin{equation*}
\frac{1}{2} \ket{1} \Big[ \ket{f_i(0)} - \ket{1 + f_i(0)} \Big]
\end{equation*}](../../assets/latex/quantum_mechanics_75da0a1b715f19feb0448aca6e065e4c22ab62a0.png)
i.e. just by looking at the control gate  , we get the answer!
, we get the answer!
Grover's algorithm
- Search algorithm
- Reduces time-complexity to
 wrt. number of items
wrt. number of items 
Cohen-Tannoudji - Quantum Mechanics
1. Waves and particles
Equations
Planck-Einstein relations
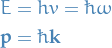
where  is the wave vector s.t.
is the wave vector s.t.  .
.
de Broglie
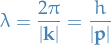
Eigenstates
With each eigenvalu  is associated an eigenstate, i.e. an eigenfunction
is associated an eigenstate, i.e. an eigenfunction  s.t.
s.t.  where
where  is the time the measurement is performed, i.e. the measurement will always yield the same
is the time the measurement is performed, i.e. the measurement will always yield the same  .
.
Scröding equation

where  is the Laplacian operator
is the Laplacian operator 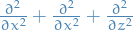 .
.
- Free particle
No force acting on the particle →

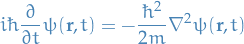
which has the solution

on the condition that
 and
and  satisty the relation:
satisty the relation:
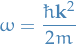
According to de Broglie we have:
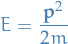
which is the same as in the classical case (no potential → only kinetic → get the above).
A plane wave of this type represents a particle whose probability of presence is uniform throughout all space :
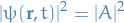
- Form of the superposition
Principle of superposition tells us that every lin. comb. of plane waves satistfying the relation for
 specified above, will also be a solution of the free-particle Schrödinger equation.
specified above, will also be a solution of the free-particle Schrödinger equation.
This super-position can be written:
![\begin{equation*}
\psi(\mathbf{r}, t) = \frac{1}{(2 \pi)^{3/2}} \int g(\mathbf{k}) e^{i [\mathbf{k} \cdot \mathbf{r} - \omega(\mathbf{k}) t]} d^3 k
\end{equation*}](../../assets/latex/quantum_mechanics_ae6f4147eda15fe7768be6390dc004fc547d3a36.png)
where
 represents the coefficients, and we integrate over all possible
represents the coefficients, and we integrate over all possible  (
( ).
).
- Form of the superposition
- Time-independent potential
In the case of a time-independent potential,
 we have:
we have:

where
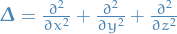 is the Laplacian operator .
is the Laplacian operator .
- Separation of variables. Stationary states
- Separation of variables
By making the assumption that
 can be separated as follows:
can be separated as follows:

We can rearrange the Schrödinger equation as follows:
![\begin{equation*}
\frac{i \hbar}{\chi(t)} \frac{d \chi(t)}{dt} = \frac{1}{\varphi (\mathbf{r})} \Big[ - \frac{\hbar^2}{2m} \boldsymbol{\Delta} \varphi(\mathbf{r}) \Big] + V(\mathbf{r})
\end{equation*}](../../assets/latex/quantum_mechanics_f78ba49397ef630437a97e054fff0cea084e5cf0.png)
Where LHS only depends on
 while RHS only depends on
while RHS only depends on  , which is only true if both sides are equal to a constant.
, which is only true if both sides are equal to a constant.
Setting LHS to
 (just treating
(just treating  as some arbitrary constant at this point), we obtain a solution for LHS:
as some arbitrary constant at this point), we obtain a solution for LHS:

Figure why we can set it to
 .
.
Now do the same for RHS we get the final solution for the full plane wave function:

where we've let
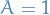 (which is fine as long as we incorporate the constant
(which is fine as long as we incorporate the constant  into
into  ).
).
The time and space variables are said to be separated .
- Stationary States
The time-independent wave function makes it so that the Schrödinger Equation only involves a single angular frequency
 . Thus, according to the Planck-Einstein relation, a stationary state is a state with a well-defined energy
. Thus, according to the Planck-Einstein relation, a stationary state is a state with a well-defined energy  (energy eigenstate).
(energy eigenstate).
We can therefore write the time-independent Schrödinger Equation as:
![\begin{equation*}
\Bigg[- \frac{\hbar^2}{2m} \boldsymbol{\Delta} + V( \mathbf{r} ) \Bigg] \varphi(\mathbf{r}) = E \varphi(\mathbf{r})
\end{equation*}](../../assets/latex/quantum_mechanics_9b07c50c656a0d2ed93a0d6759889fb3b646790b.png)
or:

where
 is the differential operator :
is the differential operator :
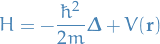
Which is a linear operator.
Thus
 tells us that
tells us that  applied to the "eigenfunction"
applied to the "eigenfunction"  (analogous to eigenvector) yields the same function, but multiplied by a constant "eigenvalue"
(analogous to eigenvector) yields the same function, but multiplied by a constant "eigenvalue"  .
.
The allowed energies are therefore the eigenvalues of the operator
 .
.
I'm not sure about the remark by about the eigenvalues being the only allowed energies..
- Superposition of stationary states
We can then distinguish between the various possible values of the energy
 (and the corresponding eigenfunctions
(and the corresponding eigenfunctions  ), by labeling them with an index
), by labeling them with an index  :
:

and the stationary states of the particle have as wave functions:

And since
 is a linear operator , we have a have series of other solutions of the form:
is a linear operator , we have a have series of other solutions of the form:

- Separation of variables
- Separation of variables. Stationary states
- Requirements
A system composed of only one particle → total probability of finding the particle anywhere in space, at time
 , is equal to
, is equal to  :
:

We therefore require that the wave-function
 must be square-integrable :
must be square-integrable :
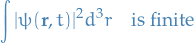
This is NOT true for the simplest solution to the Scröding equation:

Where we have
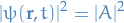
And thus,

Hence it's NOT square-integrable.
They then say: "Therefore, rigorously, it cannot represent a physical state of the particle. On the other hand, a superposition of plane waves like [this one] can be square-integrable."
Heisenberg
- Deduction
Here we only consider the 1D case, allowing us to write the wave function as as superposition of over all possible
 :
:
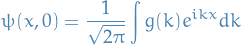
Suppose that
 has the following shape:
has the following shape:

Now let
 be a function of
be a function of  s.t. :
s.t. :

Further, we assume that
 varies sufficently smoothly within the interval
varies sufficently smoothly within the interval ![$\Big[ k_0 - \frac{\Delta k}{2}, k_0 + \frac{\Delta k}{2} \Big]$](../../assets/latex/quantum_mechanics_0e943d3d48b06a789436f83cc1dd121bfa654e1b.png) . Then, when
. Then, when  is sufficiently small, we can approx.
is sufficiently small, we can approx.  using it's tangent / linear approximation about the point
using it's tangent / linear approximation about the point 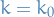 :
:
![\begin{equation*}
\alpha(k) \simeq \alpha(k_0) + (k - k_0) \Big[ \frac{d \alpha}{d k} \Big]_{k = k_0}
\end{equation*}](../../assets/latex/quantum_mechanics_d991183de79508e6abb72ab5085133f80c3663e4.png)
which enables us to write the wave-function as:
![\begin{equation*}
\psi(x, 0) \simeq \frac{e^{i [k_0 x + \alpha(k_0)]}}{\sqrt{2 \pi}} \int_{-\infty}^{+\infty} |g(k)| e^{i(k - k_0)(x - x_0)} dk
\end{equation*}](../../assets/latex/quantum_mechanics_a2d7c405a98405c30a79084d18b650bf524a409e.png)
where
![\begin{equation*}
x_0 = - \Big[ \frac{d \alpha}{d k} \Big]_{k=k_0}
\end{equation*}](../../assets/latex/quantum_mechanics_7077a6149e94ccc5a218ec7faaae09483f8fafca.png)
I belive this note turned out to be that it was in fact integrating from
 to
to  .
.
I presume that when they write
 they mean "integrate from
they mean "integrate from  to
to 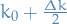 ..right? Since the "width"
..right? Since the "width"  "contains" most of the integral.
"contains" most of the integral.
This gives us a useful way of studying the variations of
 in terms of
in terms of  .
.
- If
 is large, i.e.
is large, i.e.  is far from
is far from  ,
,  will oscillate a very large number of times within the interval
will oscillate a very large number of times within the interval  . Due to the high frequency the osciallations will cancel eachother out, thus
. Due to the high frequency the osciallations will cancel eachother out, thus 
- If
 is small, i.e.
is small, i.e.  is close to
is close to  ,
,  will barely oscillate, and so we will end up with
will barely oscillate, and so we will end up with  being a maximum.
being a maximum.
- Relating to momentum
As seen previously,
 appears as a linear superposition of the momentum eigenfunctions in which the coefficient of
appears as a linear superposition of the momentum eigenfunctions in which the coefficient of  is
is  . We are thus led to interpret
. We are thus led to interpret  (to within a constant factor) as the probability of finding
(to within a constant factor) as the probability of finding  if one measures, at
if one measures, at  , the momentum of a particle whose state is described by
, the momentum of a particle whose state is described by  .
.
The possible values of
 , like those of
, like those of  , form a continuous set, and
, form a continuous set, and  is proportional to a probability density : the probability
is proportional to a probability density : the probability  of obtaining a value of between
of obtaining a value of between  and
and  is, to within a constant factor
is, to within a constant factor  . More precisely, we can rewrite the formula as:
. More precisely, we can rewrite the formula as:

we know that
 and
and  satisfy the Bessel-Parseval relation:
satisfy the Bessel-Parseval relation:
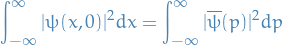
We then have
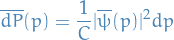
which is the probability that the measurement of the momentum will yield a result included between
 and
and  .
.
Then, writing the relation
Honestly, I'm not seeing this.
This is based on the argument that
 for the
for the  to be significant, which I don't get.
to be significant, which I don't get.
- If
- Q & A
- DONE We're assuming a certain "family" of distribution for k; does this affect our deduction?
This
 represents the coefficients for each of the different wave-functions ("different" meaning parametrized with different
represents the coefficients for each of the different wave-functions ("different" meaning parametrized with different  , and thus different wavelength / frequency), allowing us to write some arbitrary wave-function as a superposition of an infinite number of plane waves.
, and thus different wavelength / frequency), allowing us to write some arbitrary wave-function as a superposition of an infinite number of plane waves.
Why should it follow the "distribution" shown above? Why can't
 have an arbitrary "distribution", e.g. multiple peaks?
have an arbitrary "distribution", e.g. multiple peaks?
- DONE What's up with the alphas on the boundary of the integrals?
- DONE Why is it the complex conjugate of the wave equation when writing it as a function of the momentum?
- DONE We're assuming a certain "family" of distribution for k; does this affect our deduction?
Wave equation for free particle
Separable solution in as a function of  and
and 

or
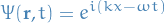
Complements
H: Stationary States of particle in one-dimensional square potential "well"
- Setup
Here we consider the time-independent Schrödinger Equation with a step-wise constant potential .
Thus, the time-independent Schrödinger Equation becomes:

- Stationary wave-function in different potentials
We can solve the TISE with constant potential using integrating factors:
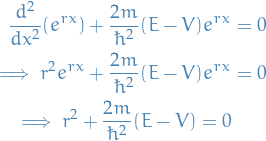
which we can be solved as a regular quadratic:
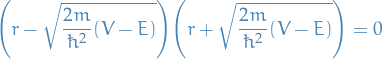

then whether or not we have a complex solution depends on whether or not
 is non-negative or not.
is non-negative or not.
- E > V - energy of particle is GREATER than potential barrier
We write (
 being defined by the the following equation)
being defined by the the following equation)
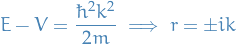
Then the stationary solution to the TISE with constant potential can be written

where
 and
and 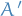 are complex constants.
are complex constants.
- E < V - energy of particle is LOWER than potential barrier
Let
 be defined by the following equation
be defined by the following equation
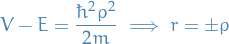
with solution to TISE with constant potential can be written:

where
 and
and  are complex constants
are complex constants
Different order of
 and
and  on LHS.
on LHS.
Also notice the fact that using the "integrating factor" to solve the ODE, our exponentials aren't positive in this case.
- E = V - energy of particle is equivalent to the potential barrier
In this case we simply end up with the differential equation
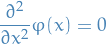
Which we can simply integrate twice and obtain a linear function expression for
 .
.
- E > V - energy of particle is GREATER than potential barrier
- Stationary wave-function at potential energy discontinuity
- Computation outline
- Solve the TISE with constant potential using integrating factors, leaving you with a quadratic.
- Let
 be such that
be such that  , for convenience
, for convenience - Obtain a general solution for both wave-functions depending on the
 in the different regions.
in the different regions. - Assume the wave-function to be continues across the boundaries (discontinuities of the potential), i.e. we require
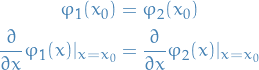
- Solve for the coefficients of the general solutions obtained.

In some cases, solving for all coefficients of the different wave-functions is not possible due to not having enough constraints.
In this case it might make sense to set some constant to zero, and instead solve for the ratios , not the coefficients themselves. Solving for ratios reduces the order of the system of equations by 1, and setting one of them to zero reduces it further by 1. In the case were we have a simple potential barrier in 1D, using the above methods to reduce the order then allows us to compute solve equations for the ratios, providing us with a reflection coefficient (which also implies a transmission coefficient ) and thus the probability of reflecting of the barrier.
- Potential well

We would follow the same as described above, but now we would have three wave functions, with boundary conditions:
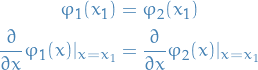
for the left side of the potential-well at
 , and for the right side at
, and for the right side at  :
:
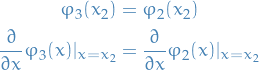
i.e. we simply use the exact same method, but now we have an additional boundary to consider.
The solution ends up looking as:
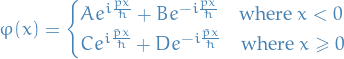
where we note that if we have a particle coming from the left, we set the coefficient of the left-traveling before the barrier to 0:
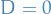
i.e. we can
We can "think" of each of these terms in the wave-function to be a super-position of eigenstates. Viewing it in that way, it makes a bit more sense I suppose.
- Infinite potential well
Same procedure as regular potential well, but now the wave-functions
 and
and  (i.e. wave-functions outside of the potential well) are equal to zero for all
(i.e. wave-functions outside of the potential well) are equal to zero for all  ! That is,
! That is,

This leads us to the quantization of energies , where we have multiple solutions satisfying the boundary conditions specified above. If the potential well is of "width"
 , we end up with the solution
, we end up with the solution
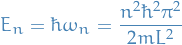
Which falls out of the fact that the boundary conditions above corresponds to the inverse wave-length being a integer multiple of the width of the potential well.
Each of these energy levels have their own eigen-function
 .
.
- Computation outline
2. The mathematical tools of quantum mechanics
Notation
 is the set of all square-integrable functions which are everywhere defined, continuous and infinitively differentiable. Together with the inner product
is the set of all square-integrable functions which are everywhere defined, continuous and infinitively differentiable. Together with the inner product  this defines a Hilbert space
this defines a Hilbert space denotes a wave function
denotes a wave function is a ket or ket vector, which is an element or vector of
is a ket or ket vector, which is an element or vector of  space, e.g.
space, e.g. 
 is the state space of a particle, and is a subspace of a Hilbert space. It's defined such that we associate each square-integrable function
is the state space of a particle, and is a subspace of a Hilbert space. It's defined such that we associate each square-integrable function  with a ket vector, i.e.
with a ket vector, i.e. 
 is the state space of a (spinless) particle in only one dimension
is the state space of a (spinless) particle in only one dimension is associated with a complex number, which is the scalar product, satisfying the properties of an inner product.
is associated with a complex number, which is the scalar product, satisfying the properties of an inner product. denotes the set of linear functionals defined on the kets
denotes the set of linear functionals defined on the kets  , which constitutes a vector space, called the dual space of
, which constitutes a vector space, called the dual space of  .
. is a bra or bra vector of the space
is a bra or bra vector of the space  , which represents a linear functional
, which represents a linear functional 
 , i.e. the linear function
, i.e. the linear function  acting on the ket
acting on the ket 
 denotes a discrete basis
denotes a discrete basis denotes a continuous basis
denotes a continuous basis (
( ) denote a projection operator for a discrete (continuous) basis
) denote a projection operator for a discrete (continuous) basis denotes the degeneracy of the eigenvalue
denotes the degeneracy of the eigenvalue 
 denotes the i-th (degenerate) eigenvector corresponding to the eigenvalue
denotes the i-th (degenerate) eigenvector corresponding to the eigenvalue  , if this eigenvalue is non-degenerate then the
, if this eigenvalue is non-degenerate then the  in the super-script can be dropped
in the super-script can be dropped denotes the eigensubspace of the eigenvalue
denotes the eigensubspace of the eigenvalue  of
of 
Dirac notation
Overview
The quantum state of any physical system is characterized by a state vector, belonging to a space  which is the state space of the system.
which is the state space of the system.
"Ket" vectors and "bra" vectors
- Dual space
A linear function
 is a linear operation which associates an complex number with every ket
is a linear operation which associates an complex number with every ket  :
:

Linear functional and linear operator must NOT be confused. In both cases we're dealing with linear operations, but the former associates each ket with a complex number, while the latter associates another ket.
- Generalized kets
"Generalized kets" are functions which are not necessarily square-integrable, but whose scalar product with every function of
 exists.
exists.
These cannot, strictly speaking, represent physical states. They are merely intermediaries.
The counter-examples to the "normal" definition of a ket are in the form of limiting cases, where the result of applying the bra to the ket is well-defined, but it's not square-integrable (it diverges when taking the limit) and thus not in
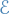 .
.
See the book at p.115 for more information about this.
But in short, in general, the dual space
 and the state space
and the state space 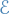 are NOT isomorphic, except if
are NOT isomorphic, except if 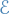 is finite-dimensional.1 I.e. the following is true:
is finite-dimensional.1 I.e. the following is true:
 2
2
But the otherway around is NOT true.
Linear operators
- Overview
Consider the operations defined by:

Choose an arbitrary ket
 and consider:
and consider:

We already know that
 ; consequently, the equation above is a ket, obtained by multiplying
; consequently, the equation above is a ket, obtained by multiplying  by the scalar
by the scalar  . Therefore the
. Therefore the  applied to some arbitrary ket
applied to some arbitrary ket  gives another ket, i.e. it's an operator.
gives another ket, i.e. it's an operator.
If
 :
:
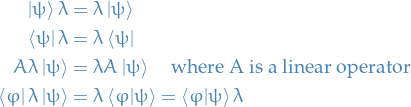
- Projections
Let
 be a ket which is normalized to one:
be a ket which is normalized to one:

Consider the operator
 defined by:
defined by:

and apply it to an arbitrary ket
 :
:

Which is simply the projection of
 onto
onto  : first take the inner product, not needing to normalize wrt.
: first take the inner product, not needing to normalize wrt.  due
due  , and then multiply by
, and then multiply by  to get the component.
to get the component.
We can also project onto a basis by taking the um over
 , and using this as an operator (applying each of them to the target ket as above). Thus we get the linear superposition .
, and using this as an operator (applying each of them to the target ket as above). Thus we get the linear superposition .
Representations in state space
- Choosing a representation amounts to choosing an orthonormal basis, either discrete or continuous, in the state space
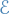
For a discrete basis 

For a continuous basis 

Representation of operators
Given a linear operator  , we can, in a
, we can, in a  or
or  basis, associate with it a series of numbers defined by
basis, associate with it a series of numbers defined by

or for a continuous basis

We can then use the closure relation to compute the matrix which represents the operator  in the
in the  basis:
basis:
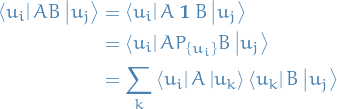
And equivalently for the continuous basis 
Matrix representation of a ket
Problem: we know the components of  and the matrix elements of the operator
and the matrix elements of the operator  in some representation. How can we compute the components of
in some representation. How can we compute the components of 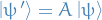 ?
?
In the  basis, the "coordinate"
basis, the "coordinate"  of
of  are given by:
are given by:
Inserting the closure relation between  and
and  , we obtain:
, we obtain:
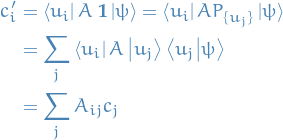
Or for a continuous basis  we have:
we have:
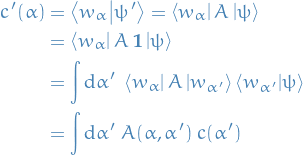
Eigenvalue equations for observables
 is said to be an eigenvector (or eigenket ) of the linear operator
is said to be an eigenvector (or eigenket ) of the linear operator  if :
if :

where  . We call the equation above the eigenvalue equation of the linear operator
. We call the equation above the eigenvalue equation of the linear operator  .
.
We say the eigenvalue  is nondegenerate if and only if the corresponding eigenvector is unique within a constant factor, i.e. when all associated eigenkets are collinear.
is nondegenerate if and only if the corresponding eigenvector is unique within a constant factor, i.e. when all associated eigenkets are collinear.
If there exists as least two linearly independent kets which are eigenvectors of  with the same eigenvalue, this eigenvalue is said to be degenerate.
with the same eigenvalue, this eigenvalue is said to be degenerate.
To be completely rigorous, one should solve the eigenvalue equation in the space 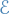 , i.e. we ought to only consider those eigenvectors
, i.e. we ought to only consider those eigenvectors  which have a finite norm.
which have a finite norm.
Unfortunately, we will be obliged to use operatores for which eigenkets do not satisfy this condition. Therefore, we shall grant that vectors which are solutions of the eigenvalue equation can be
Two eigenvectors of a Herimition operator corresponding to two different eigenvalues are orthogonal.
Consider two eigenvectors  and
and  of the Hermitian operator
of the Hermitian operator  .
.
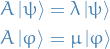
Since  is Herimition, we can write the above using the corresponding bras:
is Herimition, we can write the above using the corresponding bras:

Multiplying the above on the left with  on the right:
on the right:
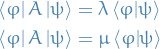
Which implies

Hence, if  we have orthogonality, i.e.
we have orthogonality, i.e. 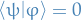 .
.
The Hermitian operator  is an observable if the orthonormal system of eigenvectors of
is an observable if the orthonormal system of eigenvectors of  , described by
, described by
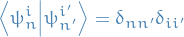
form a basis in the state space. That is,
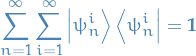
Sets of commuting observables
Consider an observable  and a basis of
and a basis of  composed of eigenvectors
composed of eigenvectors  of
of  .
.
If none of the eigenvalues of  is degenerate, then the various basis vectors of
is degenerate, then the various basis vectors of  can be labelled by the eigenvalue
can be labelled by the eigenvalue  , and all the eigensubspaces
, and all the eigensubspaces  are then one-dimensional. That is, there exists a unique basis of
are then one-dimensional. That is, there exists a unique basis of  formed by the eigenvectors of
formed by the eigenvectors of  . We then say that the observable
. We then say that the observable  constitutes, by itself, a C.S.C.O.
constitutes, by itself, a C.S.C.O.
If, on the other hand, one or several eigenvalues of  are degenerate, then the basis of eigenvectors of
are degenerate, then the basis of eigenvectors of  is not unqiue. We then choose another observable
is not unqiue. We then choose another observable  which commutes with
which commutes with  , and construct an orthonormal basis of eigenvectors common to
, and construct an orthonormal basis of eigenvectors common to  and
and  . By definition,
. By definition,  and
and  form a C.S.C.O. if this basis is unique (to within a phase factor for each of the basis vectors), that is, if, to each of the possible pairs of eigenvalues
form a C.S.C.O. if this basis is unique (to within a phase factor for each of the basis vectors), that is, if, to each of the possible pairs of eigenvalues 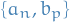 , there corresponds only one basis vector.
, there corresponds only one basis vector.
If we still don't have a C.S.C.O., we can introduce another Hermitian operator  which commutes with
which commutes with  and
and  , and then try to construct unique triples, and so on. This can be performed an arbitrary number of times in an attempt to obtain a C.S.C.O.
, and then try to construct unique triples, and so on. This can be performed an arbitrary number of times in an attempt to obtain a C.S.C.O.
A set of observables 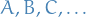 is called a complete set of commuting observables if
is called a complete set of commuting observables if
- All the observables
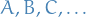 commute by pairs
commute by pairs - Specifying the eigenvalues of all the operators
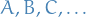 determines aa unique (to within a multiplicative factor) common eigenvector
determines aa unique (to within a multiplicative factor) common eigenvector
If 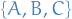 is a C.S.C.O., the specification of the eigenvalues
is a C.S.C.O., the specification of the eigenvalues  determines a ket of the corresponding basis (to within a constant factor), which we sometimes denote by
determines a ket of the corresponding basis (to within a constant factor), which we sometimes denote by 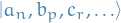
Principles of Quantum Mechanics - Dirac
Notation
 denotes an eigenket belonging to the eigenvalue
denotes an eigenket belonging to the eigenvalue  of the dynamical variable or a real linear operator
of the dynamical variable or a real linear operator 
- If
 is an eigenvalue with multiple corresponding eigenkets, then
is an eigenvalue with multiple corresponding eigenkets, then  denotes the ith corresponding eigenket
denotes the ith corresponding eigenket
Definitions
Words
- conjugate complex
- refers to the complex conjugate of a number
- conjugate imaginary
- the bra
 corresponding to the ket
corresponding to the ket 
- commutative operators

Linear Operators
Notation
 defines applying an operator to a bra
defines applying an operator to a bra
Theorems
Orthogonality theorem
Two eigenvectors of a real dynamical variable belonging to different eigenvalues are orthogonal .
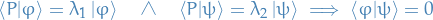
Existence of eigenvectors / eigenvalues
- Simple case
Assume that the real linear operator
 satisfies the algebraic equation:
satisfies the algebraic equation:

which means that the linear operator
 produces the result zero when applied to any ket vector or to any bra vector.
produces the result zero when applied to any ket vector or to any bra vector.
Further, let the equation above be the simplest algebraic equation that
 satisfies. Then
satisfies. Then
- The number of eigenvalues of
 is
is 
- There are so many eigenkets of
 that any ket can be expressed as a sum of such eigenkets.
that any ket can be expressed as a sum of such eigenkets.
- The number of eigenvalues of
Observables
Assumptions
If the dynamical system is in an eigenstate of a rea dynamical variable  , belonging to the eigenvalue
, belonging to the eigenvalue  , then a measurement of
, then a measurement of  will certainly give as result the number
will certainly give as result the number  . Conversely, if the system is in a state such that a measurement of a real dynamical variable
. Conversely, if the system is in a state such that a measurement of a real dynamical variable  is certain to give on particular result (instead of giving one or other of several possible results according to a probability law, as in the general case) then the state is an eigenstate of
is certain to give on particular result (instead of giving one or other of several possible results according to a probability law, as in the general case) then the state is an eigenstate of  and the result of the measurement isthe eigenvalue of
and the result of the measurement isthe eigenvalue of  to which this eigenstate belongs.
to which this eigenstate belongs.
I.e. we assume eigenstates to be the the case when a measurement of a real dynamical variable  is certain to give one particular result.
is certain to give one particular result.
Equations
Quantum Theory for Mathematicians
Notation
 represents the Hilbert space over
represents the Hilbert space over 
- Linear operator
 , with
, with  being the adjoint of
being the adjoint of 
 denotes smooth functiosn on
denotes smooth functiosn on  with compact support
with compact support
2. A First Approach to Classical Mechanics
2.5 Poisson Brackets and Hamiltonian Mechanics
Let  and
and 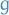 be two smooth functions on
be two smooth functions on  , where an element of
, where an element of  is thought of as a pair
is thought of as a pair  , with
, with
 representing position of a particle
representing position of a particle
 representing the momentum of a particle
representing the momentum of a particle
Then the Poisson bracket of  and
and  , denoted
, denoted 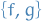 is the function on
is the function on  given by
given by
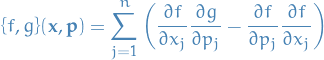
For all smooth functions  ,
,  and
and  on
on 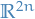 we have the following:
we have the following:
 for all
for all 
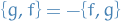
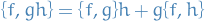
Jacobi identity:

The position and momentum functions satisfy the following Poisson bracket relations:
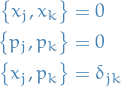
If a particle in 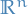 has the usual sort of energy function (kinetic energy plus potential energy), we have
has the usual sort of energy function (kinetic energy plus potential energy), we have
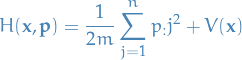
With the Hamiltonian, and as usual, having  , we can write Netwon's laws as:
, we can write Netwon's laws as:
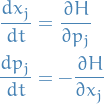
These equations we refer to has Hamilton's equations.
If  is a solution of the Hamilton's equation, then for any function
is a solution of the Hamilton's equation, then for any function  on
on  , we have
, we have
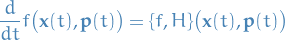
Call a smooth function  on
on  a conserved quantity if
a conserved quantity if  is independent of
is independent of  for each solution
for each solution  of Hamilton's equations.
of Hamilton's equations.
Then  is a conserved quantity if and only if
is a conserved quantity if and only if

In particular, the Hamiltonian  is a conserved quantity.
is a conserved quantity.
Solving Hamilton's equatons on  gives rise to a flow on
gives rise to a flow on  , that is, a family
, that is, a family  of diffeomorphisms of
of diffeomorphisms of 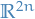 , where
, where  is equal to the solution at time
is equal to the solution at time  of Hamilton's equations with initial conditions
of Hamilton's equations with initial conditions  .
.
Since it is possible (depending on the choice of potential function  ) that a particle can escape to infinity in finite time, the maps
) that a particle can escape to infinity in finite time, the maps  are not necessarily defined on all of
are not necessarily defined on all of 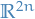 , but only on some subset therof.
, but only on some subset therof.
If  is defined on all of
is defined on all of 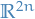 we say it's complete.
we say it's complete.
The flow associated with Hamilton's equations, for an arbitrary Hamitonian function  , preserves the (2n)-dimensional volume measure
, preserves the (2n)-dimensional volume measure
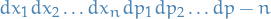
What this means, more precisely, is that if a measurable set  is contained in the domain of
is contained in the domain of  for some
for some  , then the volume of
, then the volume of  is equal to the volume of
is equal to the volume of  .
.
3. A First Approach to Quantum Mechanics
3.2 A Few Words About Operators and Their Adjoints
Linear operator
 is bounded if
is bounded if

For any bounded operator
 , there is a unique bounded operator
, there is a unique bounded operator 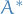 , called the adjoint of
, called the adjoint of  , such that
, such that
- Existence of
 follows from the Riesz Theorem
follows from the Riesz Theorem
For any bounded linear operator  there is a unique bounded operator
there is a unique bounded operator  , called the adjoint of
, called the adjoint of  , such that
, such that
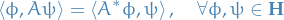
The existence of 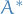 follows from Riesz Theorem.
follows from Riesz Theorem.
We say  is self-adjoint if
is self-adjoint if 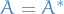 .
.
Further, if  is a linear operator defined on all of
is a linear operator defined on all of  and having the property that
and having the property that
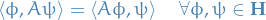
then  is automatically bounded.
is automatically bounded.
This means that an unbounded operator cannot be defined on the entire  !
!
An unbounded operator  on
on  is a linear map from a dense subspace
is a linear map from a dense subspace  into
into  .
.
Then  is "not necessarily bounded", since nothing in the definition prevents us from having
is "not necessarily bounded", since nothing in the definition prevents us from having 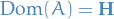 and having
and having  be bounded.
be bounded.
For an unbounded operator  on
on  , the adjoint
, the adjoint 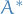 of
of  is defined as follows:
is defined as follows:
A vector  belongs to the domain
belongs to the domain  of
of 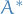 if the linear functional
if the linear functional
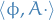
defined on  , is bounded.
, is bounded.
For  , let
, let 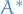 be the unique vector
be the unique vector  such that
such that
Since  is bounded and
is bounded and  is, by definition of a unbounded operator, dense, the BLT theorem tells us that
is, by definition of a unbounded operator, dense, the BLT theorem tells us that  has a unique bounded extension to all of
has a unique bounded extension to all of  .
.
Further, Riesz theorem then guarantees the existence and uniqueness of  , the corresponding vector such that
, the corresponding vector such that

Thus, the adjoint of a unbounded operator is a linear operator on  .
.
An unbounded operator  on
on  is symmetric if
is symmetric if

The operator  is self-adjoint if
is self-adjoint if

Finally,  is essentially self-adjoint if the closure in
is essentially self-adjoint if the closure in  of the graph of
of the graph of  is the graph of a self-adjoint operator.
is the graph of a self-adjoint operator.
3.6 Axioms of Quantum Mechanics: Operators and Measurements
The state of the system is represent by a unit vector  in an appropriate Hilbert space
in an appropriate Hilbert space  .
.
If  and
and  are two unit vectors in
are two unit vectors in  with
with 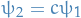 for some constant
for some constant  , then
, then  and
and  represent the same physical state.
represent the same physical state.
There is a more general notion of a "mixed state", which we will consider later.
To each real-valued function  on the classical phase space there is associated a self-adjoint operator
on the classical phase space there is associated a self-adjoint operator  on the quantum Hilbert space.
on the quantum Hilbert space.
"Quantum Hilbert space" simply means "the Hilbert space associated with a given quantum system".
If a quantum system is in a state described by a unit vector  , the probability distribution for the measurement of some observable
, the probability distribution for the measurement of some observable  satisfies
satisfies
![\begin{equation*}
\mathbb{E}[f^m] = \left\langle \psi, \big( \hat{f} \big)^m \psi \right\rangle
\end{equation*}](../../assets/latex/quantum_mechanics_8ff7f2646264c7f3bf12273db440e263ced746ad.png)
In particular, the expectation value for a measurement of  is given by
is given by

Suppose a quantum system is initially in a state  and that a measurement of an observable
and that a measurement of an observable  is performed.
is performed.
If the result of the measurement is the number  , then immediately after the measurement, the system will be in a state
, then immediately after the measurement, the system will be in a state  that satisfies
that satisfies

The passage from  to
to  is called the collapse of the wave function. Here
is called the collapse of the wave function. Here  is the self-adjoint operator associated with
is the self-adjoint operator associated with  by Axiom 2.
by Axiom 2.
The time-evolution of the wave function  in a quantum system is given by the Schödinger equtaion,
in a quantum system is given by the Schödinger equtaion,
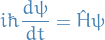
Here  is the operator corresponding to the classical Hamiltonian
is the operator corresponding to the classical Hamiltonian  by means of Axiom 2.
by means of Axiom 2.
3.8 The Heisenberg Picture
In the Heisenberg picture, each self-adjoint operator  evolves in time according to the operator-valued differential equation
evolves in time according to the operator-valued differential equation
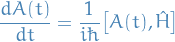
where  is the Hamiltonian operator of the system, where
is the Hamiltonian operator of the system, where  is the commutation, given by
is the commutation, given by

4. The Free Schrödinger Equation
Notation
4.2 Solution as a convolution
"Free" means that there is no force acting on the particle, so that we may take the potential  to be identically zero.
to be identically zero.
Thus, the free Scrhödinger equation is
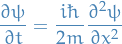
subject to an initial condition of the form

Suppose that  is a "nice" function, for example, a Schwartz function.
is a "nice" function, for example, a Schwartz function.
Let  denote the Fourier transform of
denote the Fourier transform of  and define
and define  by
by

where  is defined by
is defined by
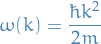
Then  solves the free Schödinger equation with initial condition
solves the free Schödinger equation with initial condition  .
.
5. A Particle in a Square Well
6. Perspectives on the Spectral Theorem
Notation
 denotes the position operator given by
denotes the position operator given by

acting on

 is a self-adjoint operator
is a self-adjoint operator- Borel set
 of
of 
 denotes the closed span of all eigenvectors of
denotes the closed span of all eigenvectors of  with eigenvalues in
with eigenvalues in 
- In cases where
 does not have true orthonormal basis,
does not have true orthonormal basis,  is called spectral subspace
is called spectral subspace
- In cases where
 is the orthogonal projection onto
is the orthogonal projection onto 
For any unit vector
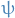 , we have
, we have

Indicator function
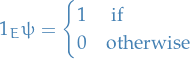
Goals of Spectral Theory
Recall that if the eigenvalues are distinct and
 decomposes as
decomposes as

the probability of observing the value
 will be
will be  ., since
., since  is just the projection onto
is just the projection onto  .
.
- In cases where
 does not have a true orthonormal basis of eigenvectors, we would like the spectral theorem to provide a family of projection operators
does not have a true orthonormal basis of eigenvectors, we would like the spectral theorem to provide a family of projection operators 
- One for each Borel subset

- Will allow us to define probabilities as in "standard" case above
- One for each Borel subset
- Call these projection operators spectral projects and the associated subspaces
 spectral subspaces.
spectral subspaces. - Intuitively,
 may be thought of as the closed span of all the generalized eigenvectors with eigenvalues in
may be thought of as the closed span of all the generalized eigenvectors with eigenvalues in  .
.
Position operator
- Has no true eigenvectors, i.e. no eigenvecors that are actually in

If we think that "generalized eigenvectors" for
 are the distributions given by
are the distributions given by

then one might guess that spectral subspace
 should consist of those functions that are "supported" on
should consist of those functions that are "supported" on  , i.e. a superposition of the "funtions"
, i.e. a superposition of the "funtions"  with
with  should define a function supported on
should define a function supported on  .
.
Spectral projection
 is then orthogonal projection onto
is then orthogonal projection onto  :
:

then

- The functional calculus of

- If
 then we should have
then we should have 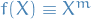
- If
7. Spectral Theorem for Bounded Self-Adjoint Operators
Notation
 is the separable complex Hilbert space
is the separable complex Hilbert spaceOperator norm of
 on
on  is
is

is finite.
- Banach space of bounded operators on
 , wrt. operator norm is denoted
, wrt. operator norm is denoted  .
.  denotes the resolvent set of
denotes the resolvent set of 
 denotes the spectrum of
denotes the spectrum of 
 denotes the projection-valued measure associated with the operator self-adjoint
denotes the projection-valued measure associated with the operator self-adjoint 
For any projection-vauled measure
 and
and  , we have an ordinary (positive) real-valued measure
, we have an ordinary (positive) real-valued measure  given by
given by

 is a map defined by
is a map defined by
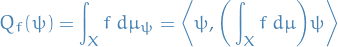
Spectral subspace for each Borel set


of

 defines a simultanouesly orthonormal basis for a family
defines a simultanouesly orthonormal basis for a family 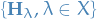 of separable Hilbert spaces
of separable Hilbert spaces
Properties of Bounded Operators
Linear operator
 on
on  is said to be bounded if the operator norm of
is said to be bounded if the operator norm of 

is finite.
Space of bounded operators on
 forms a Banach space under the operator norm, and we have the inequality
forms a Banach space under the operator norm, and we have the inequality

for all bounded operators on
 and
and  .
.
For 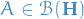 , the resolvent set of
, the resolvent set of  , denoted
, denoted  is the set of all
is the set of all  such that the operator
such that the operator 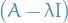 has a bounded inverse.
has a bounded inverse.
The spectrum of  , denoted by
, denoted by  , is the complement in
, is the complement in  of the resolvent set.
of the resolvent set.
For  in the resolvent set of
in the resolvent set of  , the operator
, the operator  is called the resolvent of
is called the resolvent of  at
at  .
.
Alternatively, the resolvent set of  can be described as the set of
can be described as the set of  for which
for which  is one-to-one and onto.
is one-to-one and onto.
For all  , the following results hold.
, the following results hold.
- The spectrum
 of
of  is closed, bounded and nonempty subset of
is closed, bounded and nonempty subset of  .
. - If
 , then
, then  is in the resolvent set of
is in the resolvent set of 
Point 2 in proposition:hall13-quant-7.5 establishes that  is bounded if
is bounded if  is bounded.
is bounded.
Suppose  satisfies
satisfies  .
.
Then the operator 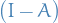 is invertible, with the inverse given by the following convergent series in
is invertible, with the inverse given by the following convergent series in  :
:

For all 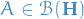 , we have
, we have
![\begin{equation*}
\big[ \text{Range}(A) \big]^{\perp} = \text{ker}(A^*)
\end{equation*}](../../assets/latex/quantum_mechanics_041fde8f7e956e923e6e23df6a01ead0a29b2641.png)
Spectral Theorem for Bounded Self-Adjoint Operators
Given a bounded self-adjoint operator  , we hope to associate with each Borel set
, we hope to associate with each Borel set 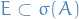 a closed subspace
a closed subspace  of
of  , where we think intuitively that
, where we think intuitively that  is the closed span of the generalized eigenvectors for
is the closed span of the generalized eigenvectors for  with eigenvalues in
with eigenvalues in  .
.
We would expect the following properties of these subspaces:
 and
and 
- Captures idea that generalized eigenvectors should span

- Captures idea that generalized eigenvectors should span
- If
 and
and  are disjoint, then
are disjoint, then 
- Generalized eigenvectors ought to have some sort of orthogonality for distinct eigenvalues (even if not actually in
 )
)
- Generalized eigenvectors ought to have some sort of orthogonality for distinct eigenvalues (even if not actually in
- For any
 and
and  ,
, 
If
 are disjoint and
are disjoint and  , then
, then
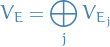
- For any
 ,
,  is invariant under
is invariant under  .
. If
![$E \subset [\lambda_0 - \varepsilon, \lambda_0 + \varepsilon]$](../../assets/latex/quantum_mechanics_bec5a95e47e8417fb8c1111121dd55490ad968ee.png) and
and  , then
, then

Projection-Valued measures
For any closed subspace  , there exists a unique bounded operator
, there exists a unique bounded operator  such that
such that

where  is the orthogonal complement.
is the orthogonal complement.
This operator is called the orthogonal projection onto  and it satisfies
and it satisfies

i.e. it's self-adjoint.
One also has the properties

or equivalently,
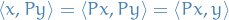
Conversely, if  is any bounded operator on
is any bounded operator on  satisfying
satisfying  and
and  , then
, then  is the orthogonal projection onto a closed subspace
is the orthogonal projection onto a closed subspace  , where
, where

- Convenient ot describe closed subspaces of
 in terms of associated orthogonal projection operators
in terms of associated orthogonal projection operators - Projection operator expresses the first four properties of the spectral subspaces; those properties are similar to those of a measures, so we use the term projection-valued measure
Let  be a set and
be a set and  an
an  in
in  .
.
A map  is called a projection-valued measure if the following properties are satisfied:
is called a projection-valued measure if the following properties are satisfied:
- For each
 ,
,  is an orthogonal projection
is an orthogonal projection  and
and 
If
 are disjoint, then for all
are disjoint, then for all  , we have
, we have
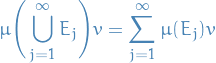
where the convergence of the sum is in the norm-topology on
 .
.
- For all
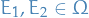 , we have
, we have 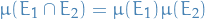
Properties 2 and 4 in of a projection-valued measure tells us that if  and
and  are disjoint, then
are disjoint, then

from which it follows that the range of  and the range of
and the range of  are perpendicular.
are perpendicular.
Let  be a
be a  in a set
in a set  and let
and let  be a projection-valued measure.
be a projection-valued measure.
Then there exists a unique linear map, denoted
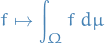
from the space of bounded, measurable, complex-valued functions on  into
into  with the property that
with the property that

for all  and all
and all  .
.
This integral has the following properties:
For all
 , we have
, we have
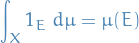
In particular, the integral of the constant function
 is
is  .
.
For all
 , we have
, we have

Integration is multiplicative: For all
 and
and  , we have
, we have
For all
 , we have
, we have
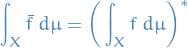
In particular, if
 is real-valued, then
is real-valued, then  is self-adjoint.
is self-adjoint.
By Property 1 and linearity, integration wrt.  has the expected behavior on simple functions. It then follows from Property 2 that the integral of an arbitrary bounded measurable function
has the expected behavior on simple functions. It then follows from Property 2 that the integral of an arbitrary bounded measurable function  can be comptued as follows:
can be comptued as follows:
- Take sequence
 of simple functions converging uniformly to
of simple functions converging uniformly to 
- The integral of
 is then the limit, in the norm-topology, of the integral of the
is then the limit, in the norm-topology, of the integral of the  .
.
A quadratic form on a Hilbert space  is a map
is a map  with the following properties:
with the following properties:
 for all
for all  and
and 
the map
 defined by
defined by
![\begin{equation*}
\begin{split}
L(\phi, \psi) =& \frac{1}{2} \big[ Q(\phi + \psi) - Q(\phi) - Q(\psi) \big] \\
& - \frac{i}{2} \big[ Q(\phi + i \psi) - Q(\phi) - Q(i \psi) \big]
\end{split}
\end{equation*}](../../assets/latex/quantum_mechanics_6085b0f14f4edf2b5f0f23825c97cba9ce1cc8de.png)
is a sesquilinear form.
A quadratic form  is bounded if there eixsts a constant
is bounded if there eixsts a constant  such that
such that

The smallest such constant  is the norm of
is the norm of  .
.
If  is a bounded quadratic form on
is a bounded quadratic form on  , there is a unique
, there is a unique  such that
such that

If  belongs to
belongs to  for all
for all  , then the operator
, then the operator  is self-adjoint.
is self-adjoint.
Spectral Theorem for Bounded Self-Adjoint Operators: direct integral approach
Notation
 is a
is a  measure on a
measure on a 
 of sets in
of sets in 
- For each
 we have a separable Hilbert space
we have a separable Hilbert space  with inner product
with inner product 
- Elements of the direct integral are called sections

Stuff
There are several benefits to this approach compared to the simpler "multiplication operator" approach.
- The set
 and the function
and the function  become canonical:
become canonical:
- The direct integral carries with it a notion of generalized eigenvectors / kets, since the space
 can be thought of as the space of generalized eigenvectors with eigenvalue
can be thought of as the space of generalized eigenvectors with eigenvalue  .
. - A simple way to classify self-adjoint operators up to unitary equivalence: two self-adjoint operators are unitarily equivalent if and only if their direct integral representations are equivalent in a natural sense.
Elements of the direct integral are called sections  , which are functions on
, which are functions on  with values in the union of the
with values in the union of the  , with property
, with property
We define the norm of a section  by the formula
by the formula

provided that the integral on the RHS is finite.
The inner product between two sections 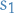 and
and  (with finite norm) should then be given by the formula
(with finite norm) should then be given by the formula
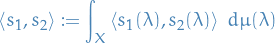
Seems very much like the differential geometry section we know of.
 is the fibre at each point
is the fibre at each point  in the mfd.
in the mfd. is the mfd.
is the mfd.
First we slightly alter the concept of an orthonormal basis. We say a family  of vectors is an orthonormal basis for a Hilbert space
of vectors is an orthonormal basis for a Hilbert space  if
if

and

This just menas that we allow some of the vectors in our basis to be zero.
We define a simultanouesly orthonormal basis for a family  of separable Hilbert spaces to be a collection
of separable Hilbert spaces to be a collection  of sections with the property that
of sections with the property that

Provided that the function  is a measurable function from
is a measurable function from  into
into ![$[0, \infty]$](../../assets/latex/quantum_mechanics_7c43cf12221cf82ea0f3550c49639ade5528d224.png) , it is possible to choose a /simultaneous orthonormal basis
, it is possible to choose a /simultaneous orthonormal basis  such that
such that

is measurable for all  and
and  .
.
Choosing a simultaneous orthonormal basis with the property that the function

is a measurable function from  into
into ![$[0, \infty]$](../../assets/latex/quantum_mechanics_7c43cf12221cf82ea0f3550c49639ade5528d224.png) , we can define a section to be measurable if the function
, we can define a section to be measurable if the function

is a measurable complex-valued function for each  . This aslo means that the
. This aslo means that the  are also measurable sections.
are also measurable sections.
We refer to such a choice of simultaneous orthonormal basis as a measurability structure on the collection  .
.
Given two measurable sections 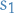 and
and  , the function
, the function
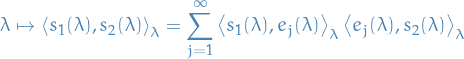
is also measurable.
Suppose the following structures are given:
- a
 measure space
measure space 
- a collection
 of separable Hilbert spaces for which the dimension function is measurable
of separable Hilbert spaces for which the dimension function is measurable - a measurability structure on

Then the direct integral of  wrt.
wrt.  , denoted
, denoted

is the space of equivalence classes of almost-everywhere-equal measurable sections  for which
for which

The inner product 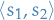 of two sections
of two sections 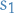 and
and  is given by the formula
is given by the formula

8. Spectral Theorem for Bounded Self-Adjoint Operators: Proofs
Notation
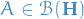 with spectral radius
with spectral radius
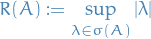
Stage 1: Continuous Functional Calculus
Stage 2: An Operator-Valued Riesz Representation Theorem
Let  be a compact metric space and let
be a compact metric space and let 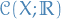 denote the space of continuous, real-valued functions on
denote the space of continuous, real-valued functions on  .
.
Suppose 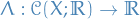 is a linear functioanl with the property that
is a linear functioanl with the property that 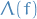 is non-negative if
is non-negative if  is non-negative.
is non-negative.
Then there exists a unique (real-valued, positive) measure  on the Borel sigma-algebra in
on the Borel sigma-algebra in  for which
for which
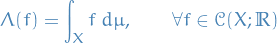
Observe that  is a finite measure, with
is a finite measure, with

where  is the constant function.
is the constant function.
Practice problems
"Point-potential"
We have a potential of the form
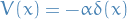
which gives us the TISE:
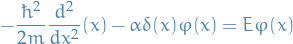
Then we impose the following conditions on the solution  :
:
- continuity at
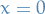 , i.e. require
, i.e. require 

The continuity restriction does NOT necessarily mean that the derivative itself is continuous!
If we then integrate both sides of the TISE above over the interval  taking the limit
taking the limit  :
:
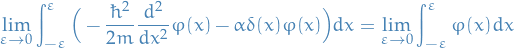
which gives us
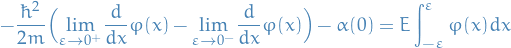
And since  , we get:
, we get:
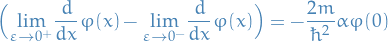
Then we compute the derivaties and take the limits, giving us something better to work with!
Harmonic Oscillator
Consider a potential energy of the form  . The classical energy is then:
. The classical energy is then:
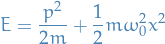
Using the Hamiltonian operator  and the momentum
and the momentum  . We can then write the Schödinger equation, letting
. We can then write the Schödinger equation, letting  and
and 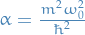 for convenience, as:
for convenience, as:
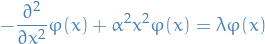
or equivalently,
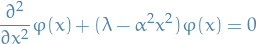
Goal is the to find solutions  that are physical and suitable for all
that are physical and suitable for all  .
.
One approach is to perform the following:
- Obtain solution for limiting behavior
- Perform power series expansion
Our requirements for the solution:
- single valued over the region (well-behaved)
First consider when 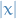 is large and
is large and  dominates with
dominates with  being negible by design . Then
being negible by design . Then

which we can guess ourselves to a solution of

to which we then note that 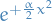 is not satisfactory given that it diverges (due to restricting out attention to square-integrable functions only). Hence,
is not satisfactory given that it diverges (due to restricting out attention to square-integrable functions only). Hence,

Why does it make sense to consider the limit behavior?
Due to the continuity imposed on the solution / wave function  we now that the solution to the limiting behavior is related to the solution across the entire domain of
we now that the solution to the limiting behavior is related to the solution across the entire domain of  .
.
From this solution we can then derive more solutions using reduction of order, i.e. we multiply our previous solution with some arbitrary function  , which gives use
, which gives use

Taking the derivatives and substituting into the original differential equation we get:
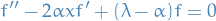
To make the connection with a "special" function in a few steps, let's make the substituion  and replace the function
and replace the function  with
with  to get the following equation:
to get the following equation:
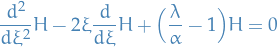
We can now represent  as a power series:
as a power series:
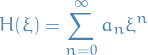
where we've made the assumption that this series converges for all  and that the function is well defined.
and that the function is well defined.
Physically, we know the above has to be case for the solutions to make sense and satisfy our overall constraint that the integral of the probability density must be finite: 
Differentiating  and substituting back into the differential equation we (eventually) obtain the recursion formula:
and substituting back into the differential equation we (eventually) obtain the recursion formula:
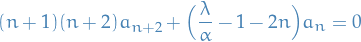
And thus we have a solution! BUT we have a serious problem :
- We assumed the series of
 to be convergent for all
to be convergent for all  which is not generally true in the recursion relation for all values
which is not generally true in the recursion relation for all values  (the energy values) and
(the energy values) and  (potential well curvature)
(potential well curvature) - The function is square integrable if
 is truncated and does not contain an infininte number of terms in its series expansion
is truncated and does not contain an infininte number of terms in its series expansion
Thus, when we then require the
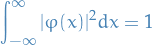
it can be seen from the recursion relation that the series expansion is finite (and hence converges  ) if
) if
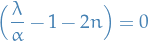
or the energy values have the folloiwgn discrete spectra,

Whiiiich we can finally write as:

Short problems
Eigenvalue expansion of in angular momentum basis
The wavefunction of a particle at  is known to have the form
is known to have the form
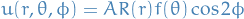
where  is an unknown function of
is an unknown function of  .
.
What can be predicted about the results of measuring:
- the z-component of angular momentum?
- the square of the angular momentum?
Hint: expand 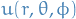 in eigenfunctions of
in eigenfunctions of  , which are of the form
, which are of the form  , where
, where  .
.
Answer
Observe that
![\begin{equation*}
\cos 2 \phi = \frac{1}{2} \Big[ e^{2 i \phi} + e^{- 2 i \phi} \Big]
\end{equation*}](../../assets/latex/quantum_mechanics_dc5f97cf97be95cf2017b3107ff0423c7fa2fb50.png)
Thus,
![\begin{equation*}
u(r, \theta, \phi) = \frac{1}{2} A R(r) f(\theta) \Big[ e^{2 i \phi} + e^{- 2 i \phi} \Big]
\end{equation*}](../../assets/latex/quantum_mechanics_aba7987d568d0e5f2a195c6870511f2ac79511fc.png)
Thus, when measuring  , we can obtain either
, we can obtain either 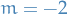 or
or 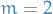 with equal probability.
with equal probability.
We can't really say anything about  , without knowing more about
, without knowing more about  , other than observing that
, other than observing that  since
since 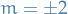 .
.
Constructing matrix for angular component of a system with 
Construct the  matrix which represent the Cartesian component in the z-direction of the angular momentum for a system with
matrix which represent the Cartesian component in the z-direction of the angular momentum for a system with  .
.
Answer
For  ,
,  , and the matrix-elements of
, and the matrix-elements of  are given by
are given by

Thus, we have
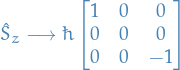
where we use  instead of
instead of  to indicate that
to indicate that  only corresponds to this matrix in this specific representation / space (Cartesian coordinates in this case).
only corresponds to this matrix in this specific representation / space (Cartesian coordinates in this case).
Q & A
Simplification of potential well problem due to direction of travel
See rmk:potential-well-simplification-due-to-travelling-direction for what I'm talking about.
Footnotes:
Is is true that the Hilbert space  and its dual space are isomorphic; however, we have taken for the wave function space
and its dual space are isomorphic; however, we have taken for the wave function space  is a subspace of
is a subspace of  , which explains why
, which explains why  is "larger" than
is "larger" than  .
.

![\begin{equation*}
\begin{split}
&= \bra{\lambda, m} \hat{J}^2 - \hat{J}_3^2 - \hbar \hat{J}_3 \ket{\lambda, m} \\
&= \hbar^2 [ j (j + 1) - m^2 - m ] \bra{\lambda m}\ket{\lambda, m} \\
&= \hbar^2 [ j (j + 1) - m^2 - m ] \\
\end{split}
\end{equation*}](../../assets/latex/quantum_mechanics_17e26b5174c4d5e56007613a2bab8d5de15ee763.png)
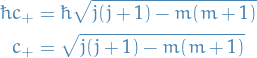

 we get
we get
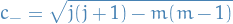


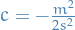


 .
.

 called the adjoint operator (or Hermitian conjugate ) of
called the adjoint operator (or Hermitian conjugate ) of 
 be s.t.
be s.t.

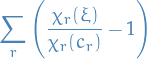
 in the above expression. In this case, each term of the sum above will be of the form:
in the above expression. In this case, each term of the sum above will be of the form:
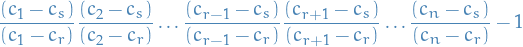
 should vanish. I get the fact that
should vanish. I get the fact that