General Relativity
Table of Contents
Notation
- IFs is inertial frames
Newtonian spacetime
Notation
Stuff
Reformulation of Poisson laws:
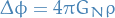
in terms of the Newtonian spacetime curvature as
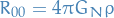
where  is the 00-component of the Ricci tensor.
is the 00-component of the Ricci tensor.
Then Newtonian spacetime is tuple 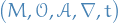 where
where
 is torsion free
is torsion free


Absolute space
Absolute space at time  is defined
is defined

and so (Newtonian) spacetime can be written as the disjoint union of the absolute spaces:
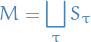
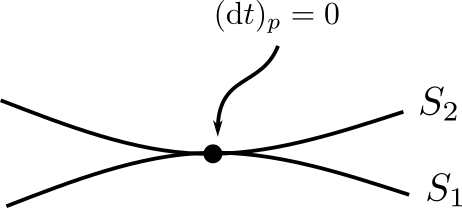
One way to visualize absolute time is as follows:

If absolute time didn't "flow uniformly", then we would allow something like the following, where we can have time standing completely still:
Motivation
Newton's laws
- Motion:
 and
and  where
where
 is the inertial mass
is the inertial mass
Gravity:
 where
where  , which satisfies the (gravitational) Poisson equation
, which satisfies the (gravitational) Poisson equation

where
 is Newton's gravitational constant
is Newton's gravitational constant is density
is density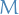 is the mass of the "source"
is the mass of the "source"
Experiment: inertial mass is equivalent to gravitational mass, i.e.
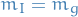
which is called the weak equivalence principle, thus

Therefore we get the fact that locally, gravity is uniform acceleration
Non-uniform
 gives rise to tidal forces. Follows from the deviation equation
gives rise to tidal forces. Follows from the deviation equation
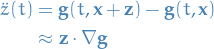
Special relativity
Spacetime
 where points are events, with inertial frames
where points are events, with inertial frames

and we use the Minkowski metric

(a quadratic form), which is invariant in all IFs. Notice

- Motion is described by wordlines
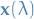
- Free motion follow straight lines
- IFs related by Poincare group (which leaves
 invariant:
invariant:
- Rotations
- Translations
- Lorentz boosts (rotation between space and time)
- Maxwell's eqns have Poincaré symmetry, but NOT Galilean symmetry (which is what Newton's gravity follows)
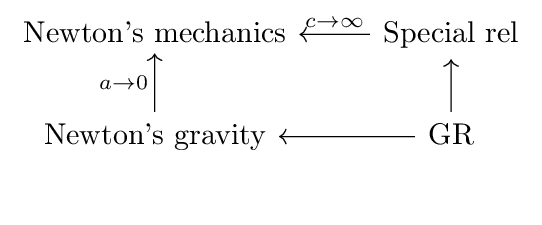
General relativity
- Laws of physics take same form in any coordinate system, i.e. invariant under general coord changes
- Will obtain by formuating laws with tensor fields
- There exists lcoal IF with no gravity, where laws are as in special relativity (called the /strong equivalence principle)
- Spacetime is (differentiable) manifold with Lorentzian metric
Postulates
Spacetime is a four-dimensional Lorentzian manifold 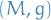 .
.
More specifically, (relativistic) spacetime is defined by the tuple 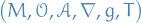 where
where
 is torsion-free
is torsion-free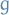 is a Lorentzian metric
is a Lorentzian metric 
 is a time-orientation
is a time-orientation
Let 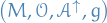 be a Lorentzian manifold.
be a Lorentzian manifold.
Then a time-orientation is given by a smooth vector field  that
that
- do not vanish anywhere, i.e.
 for all
for all 

Here  denotes an oriented atlas.
denotes an oriented atlas.
- Comparing with Newtonian spacetime we have gone from a "time"
 to a metric
to a metric 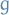 and time-orientation
and time-orientation  .
. - Reason for introducing a metric
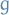 now is that we want some way of enforcing the fact that a particle cannot move faster than the speed of light
now is that we want some way of enforcing the fact that a particle cannot move faster than the speed of light If we instead considered the metric
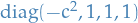 then we observe that
then we observe that
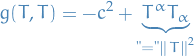
so if
 , we are basically saying that the flow along
, we are basically saying that the flow along  has a "speed" which less than the speed of light (as we want).
has a "speed" which less than the speed of light (as we want).
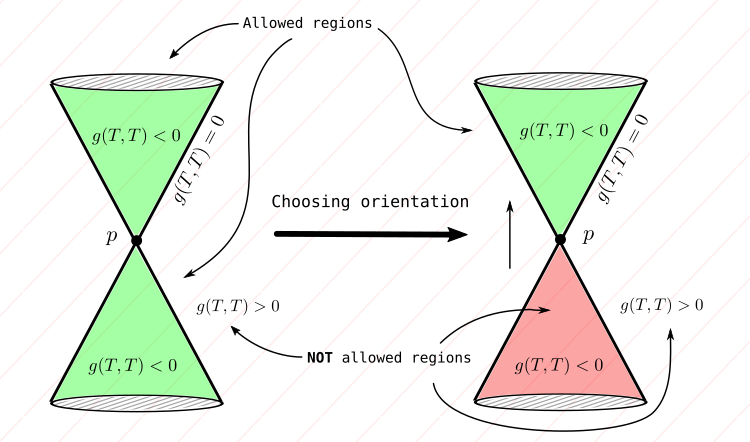
- Observe then that (with our convention), that
 is "illegal"
is "illegal"
- Observe then that (with our convention), that
- The above produces the well-known light-cone, where if we make a choice of time-orientation to enforce the fact that a particle cannot move into the past
Connections and curvature
Notation
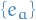 denotes a basis of a vector fields on
denotes a basis of a vector fields on 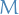
 denotes the dual basis of covector fields on $M4
denotes the dual basis of covector fields on $M4- In GR, the term connection will often be used to refer to the tensor
 ; this is because of how it relates to the connection 1-form
; this is because of how it relates to the connection 1-form Covariant derivative as a (1, 1)-tensor field

with components

Components of connection
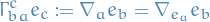
- Symmetric summation
 and anti-symmetric
and anti-symmetric ![$T_{[ab]} = \frac{1}{2} (T_{ab} - T_{ba})$](../../assets/latex/general_relativity_9672d20ad207ab54cf472d1dfebc0705c67bcf77.png)
Torsion is denoted
 or in components
or in components 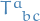 and is given by
and is given by

and in components
![\begin{equation*}
\tensor{T}{^{a}_{bc}} = - 2 \tensor{\Gamma}{^{a}_{[bc]}}
\end{equation*}](../../assets/latex/general_relativity_9ed0ab5cc30764f54c23a56993434cb5415e49b2.png)
Covariant derivative
Let 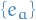 be a basis of vector fields on
be a basis of vector fields on 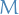 . The components of the connection
. The components of the connection  in a basis is defined by
in a basis is defined by

Letting

the covariant derivative can be written
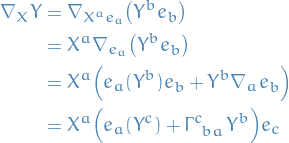
and so
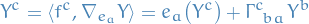
where  is the dual basis of
is the dual basis of  . In a particular coordinate basis
. In a particular coordinate basis 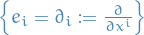

Under a basis change  and
and 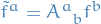 , we have
, we have

whre the basis change coefficients  .
.
In particular, under a change of coordinate basis, this becomes
![\begin{equation*}
\tensor{\tilde{\Gamma}}{^{i}_{jk}} = \pdv{\tilde{x}^i}{x^l} \pdv{x^m}{\tilde{x}^j} \pdv{x^n}{\tilde{x}^k} \tensor{\Gamma}{^{l}_{mn}} + \pdv{\tilde{x}^i}{x^l} \pdv[2]{x^l}{\tilde{x}^j}{\tilde{x}^k}
\end{equation*}](../../assets/latex/general_relativity_a63638edae388d7ae8284578c00d2d905f0dc3f3.png)
We use  to denote fixed indices, and
to denote fixed indices, and 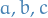 for contractible ones.
for contractible ones.
![\begin{equation*}
\begin{split}
\tensor{\tilde{\Gamma}}{^{i}_{jk}} &= \left\langle \tilde{f}^i, \nabla_{\tilde{e}_k} \tilde{e}_j \right\rangle \\
&= \left\langle \tensor{A}{^{i}_{a}} f^a, \nabla_{\tensor{(A^{-1})}{^{c}_{k}} e_c} \tensor{\big( A^{-1} \big)}{^{b}_{j}} e_b \right\rangle \\
&= \tensor{A}{^{i}_{a}} \tensor{\big( A^{-1} \big)}{^{c}_{k}} \left\langle f^a, \nabla_c \tensor{\big( A^{-1} \big)}{^{b}_{j}} e_b \right\rangle \\
&= \tensor{A}{^{i}_{a}} \tensor{\big( A^{-1} \big)}{^{c}_{k}} \Big[ \tensor{\big( A^{-1} \big)}{^{b}_{j}} \underbrace{\left\langle f^a, \nabla_c e_b \right\rangle}_{=: \tensor{\Gamma}{^{a}_{bc}}} + \left\langle f^a , e_b \right\rangle e_c \Big( \tensor{\big( A^{-1} \big)}{^{b}_{j}} \Big)\Big] \\
&= \tensor{A}{^{i}_{a}} \tensor{\big( A^{-1} \big)}{^{c}_{k}} \tensor{\big( A^{-1} \big)}{^{b}_{j}} \tensor{\Gamma}{^{a}_{bc}} + \tensor{A}{^{i}_{a}} \tensor{\big( A^{-1} \big)}{^{c}_{k}} \tensor{\delta}{^{a}_{b}} e_c \Big( \tensor{\big( A^{-1} \big)}{^{b}_{j}} \Big) \\
&= \tensor{A}{^{i}_{a}} \tensor{\big( A^{-1} \big)}{^{c}_{k}} \tensor{\big( A^{-1} \big)}{^{b}_{j}} \tensor{\Gamma}{^{a}_{bc}} + \tensor{A}{^{i}_{a}} \tensor{\big( A^{-1} \big)}{^{c}_{k}} e_c \Big( \tensor{\big( A^{-1} \big)}{^{a}_{j}} \Big)
\end{split}
\end{equation*}](../../assets/latex/general_relativity_a21674ebe5974092b8b6308565c08007921dbdee.png)
If we then let 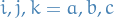 and
and  we obtain our proof (up to commutation between
we obtain our proof (up to commutation between  functions, so we're fine).
functions, so we're fine).
Moreover, in a specific chart 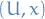 and changed basis
and changed basis  we simply have
we simply have

Substituting back into the above, we obtain our result.
Let  be a connection on a smooth manifold
be a connection on a smooth manifold 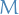 .
.
A vector field  is said to be parallely transported along a curve with tangent vector field
is said to be parallely transported along a curve with tangent vector field  if
if

The parallel transport condition in components reads
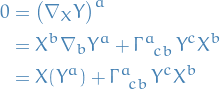
Along an integral curve  we have
we have  , and so we can write
, and so we can write
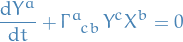
A geodesic is an integral curve of a vector field  that satisfies
that satisfies
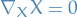
In other words, a geodesic vector field is parallely transported wrt. itself.
In a coordinate basis, the integral curves satisfy  , and so the geodesic eqation is
, and so the geodesic eqation is
![\begin{equation*}
\dv[2]{x^i}{t} + \tensor{\Gamma}{^{i}_{jk}} \Big( x(t) \Big) \dv{x^j}{t} \dv{x^k}{t} = 0
\end{equation*}](../../assets/latex/general_relativity_0fa018642bf1762d5f061424588acadcac57c584.png)
Consider a geodesic  with tangent field
with tangent field  .
.
Suppose we reparametrize the curve so that  with
with  . The tangent field of the curve
. The tangent field of the curve  is then given by
is then given by  where
where  . Thus,
. Thus,
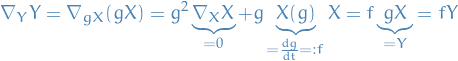
Thus, the equation  describes the same geodesic curve in a different parametrization.
describes the same geodesic curve in a different parametrization.
An affine parameter is one for which  . We deduce that this means that
. We deduce that this means that  for
for  and
and  .
.
Let  open for which
open for which  is a bijection.
is a bijection.
Normal coordinates at  , of a point
, of a point  , are given by
, are given by  where
where  are the components of
are the components of
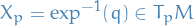
in a basis 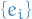 .
.
In normal coordinates at 

Consider the geodesic through 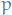 and
and  .
.
In normal coords. the geodesic takes the form
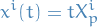
Inserting this into the geodesic equation and evaluating at  , we deduce that
, we deduce that
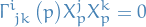
Hence

Since this is true for all  in an open set
in an open set  , we have our proof.
, we have our proof.
Torsion and curvature
Torsion
Let 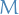 be a smooth manifold with a connection
be a smooth manifold with a connection  .
.
The torsion  is a
is a 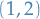 tensor defined by
tensor defined by

where  are smooth vector fields.
are smooth vector fields.
One can easily check that this is indeed a tensor.
Componentwise,
![\begin{equation*}
\begin{split}
\tensor{T}{^{i}_{jk}} &= \left\langle f^i, T(e_j, e_k) \right\rangle \\
&= \left\langle f^i, \nabla_j e_k - \nabla_k e_j \right\rangle \\
&= \tensor{\Gamma}{^{i}_{kj}} - \tensor{\Gamma}{^{i}_{jk}} \\
&= - 2 \tensor{\Gamma}{^{i}_{[jk]}}
\end{split}
\end{equation*}](../../assets/latex/general_relativity_ad86c625dc2a571ccf7def5983fd145bb99605ba.png)
Geodesics are determined by the symmetric part of the connection components  , thus the torsion does not affect the geodesics!
, thus the torsion does not affect the geodesics!
Let 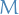 be a manifold with a connection
be a manifold with a connection  .
.
For any function  ,
,

We prove this by working in a basis 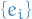 .
.
Since 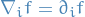 , the covariant derivative of the covector
, the covariant derivative of the covector  is
is
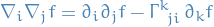
Therefore, antisymmetrising, we get
![\begin{equation*}
\nabla_i \nabla_j f - \nabla_j \nabla_i f = 2 \tensor{\Gamma}{^{k}_{[ij]}} \partial_k f = - \tensor{T}{^{k}_{ij}} \nabla_k f
\end{equation*}](../../assets/latex/general_relativity_728957436af238e8928074eb86b87f12047ceb69.png)
Since this is a relation between tensors, it follows that it must hold in any arbitrary basis.
Curvature
The Riemann curvature of a connection  is a
is a  defined by
defined by
![\begin{equation*}
R(X, Y) Z = \nabla_X \nabla_Y Z - \nabla_Y \nabla_X Z - \nabla_{[X, Y]} Z
\end{equation*}](../../assets/latex/general_relativity_46670b9c5172e188284c2939c36bc0253154e4b9.png)
where 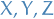 are smooth vector fields.
are smooth vector fields.
One can verify that this is indeed a tensor by checking that it's linear in  and
and  .
.
The Riemann tensor is the (1, 3) tensor defined by  , where the ordering of the arguments is standard notation. The components are then defined
, where the ordering of the arguments is standard notation. The components are then defined
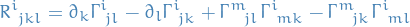
The component-wise expression for the Riemann tensor can be seen as follows:

where we first observe that
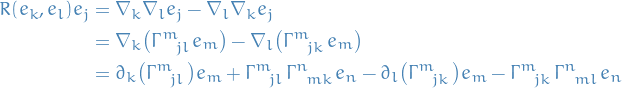
from which the Riemann tensor  immediately follows.
immediately follows.
First, observe that for a torsionless connection  , we have
, we have

Now
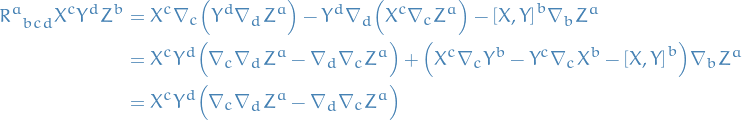
Since this holds for all  , we conclude our proof.
, we conclude our proof.
Let  be a torsionless connection.
be a torsionless connection.
For any covector field 

Ricci identity (for vectors) says that for some vector field  we have
we have

We can write 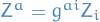 , which gives us
, which gives us
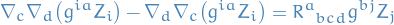
We have

so
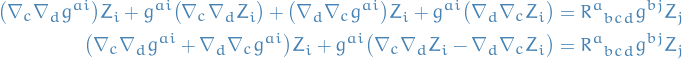
Locally
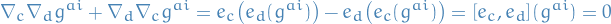
where we have dropped the resulting  terms since they commute in the lower indices.
Therefore
terms since they commute in the lower indices.
Therefore
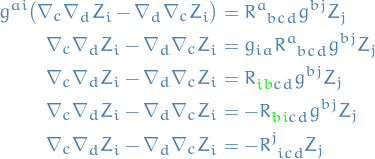
Locally the coefficients of a covector field can be expressed as 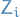 for some vector field
for some vector field  , so we simply let
, so we simply let
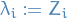
and map indices  and
and  , giving us
, giving us

Riemann tensor has an important geometrical interpretation.
It can be shown that 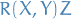 is the change in
is the change in  upon parallel transport around a small quadrilateral whose opposite sides are integral curves of vector fields
upon parallel transport around a small quadrilateral whose opposite sides are integral curves of vector fields  and
and  . Hence, if
. Hence, if 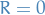 parallel transport is locally path-independent.
parallel transport is locally path-independent.
The torsion and curvature of a connection  vanish if and only if for any
vanish if and only if for any  , there exists a chart
, there exists a chart  such that
such that  and
and
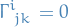
In short,
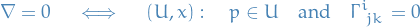
Suppose  is a torsionless connection. Then we have
is a torsionless connection. Then we have
![\begin{equation*}
\begin{split}
\tensor{R}{^{a}_{[bcd]}} &= 0 \\
\tensor{R}{^{a}_{bcd}} &= \frac{2}{3} \Big( \tensor{R}{^{a}_{(bc)d}} - \tensor{R}{^{a}_{(bd)c}} \Big)
\end{split}
\end{equation*}](../../assets/latex/general_relativity_5ae0e89452dace5428841829b0b81d3ab604d8c2.png)
We will be working in normal coordinates.
Recall that in normal coordinates at  , we have
, we have  .
.
Hence, for a torsionless connection, this reduces to  .
.
Therefore, the Riemann tensor in normal coordinates at 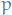 is simply
is simply

Due to anti-symmetry in the last two indices,
![\begin{equation*}
\tensor{R}{^{a}_{[bcd]}} = \frac{1}{3} \big( \tensor{R}{^{a}_{bcd}} + \tensor{R}{^{a}_{cdb}} + \tensor{R}{^{a}_{dbc}} \big)
\end{equation*}](../../assets/latex/general_relativity_1e08ec039f1f1d8e061d891ba6e93e25df445ddf.png)
Substituting in the above identity (since we are in normal coordinates),
![\begin{equation*}
\tensor{R}{^{a}_{[bcd]}} = \frac{1}{3} \big( \partial_c \tensor{\Gamma}{^{a}_{bd}} - \partial_d \tensor{\Gamma}{^{a}_{bc}} + \partial_d \tensor{\Gamma}{^{a}_{cb}} - \partial_b \tensor{\Gamma}{^{a}_{cd}} + \partial_b \tensor{\Gamma}{^{a}_{dc}} - \partial_c \tensor{\Gamma}{^{a}_{db}} \big) = 0
\end{equation*}](../../assets/latex/general_relativity_7a48494a5fbc36c070c4071381291de0115c3ee3.png)
since
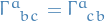 .
.
We have
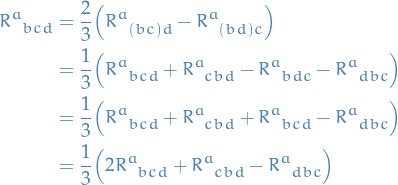
So we need the last term to equal
 . To see this we write the expressions out
. To see this we write the expressions out
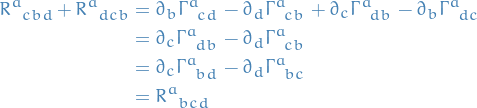
as we wanted. Substituting into the expression above,
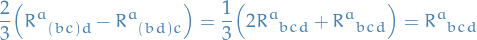
as claimed.
![\begin{equation*}
\begin{split}
\nabla_{[c} \tensor{R}{^{a}_{|b| de]}} &= \frac{1}{6} \Big( \nabla_c \tensor{R}{^{a}_{bde}} - \nabla_c \tensor{R}{^{a}_{bed}} + \nabla_e \tensor{R}{^{a}_{b cd}} - \nabla_e \tensor{R}{^{a}_{bdc}} + \nabla_d \tensor{R}{^{a}_{b ec}} - \nabla_d \tensor{R}{^{a}_{b ce}} \Big) \\
&= \frac{1}{3} \Big( \nabla_c \tensor{R}{^{a}_{bde}} + \nabla_e \tensor{R}{^{a}_{b cd}} + \nabla_d \tensor{R}{^{a}_{b ec}} \Big)
\end{split}
\end{equation*}](../../assets/latex/general_relativity_76ee9e18379884ce8bb500474dec92388d32ddc5.png)
which follows directly from

Then observe that

since in normal coordinates we have

because  since
since  . Finally, substituting this into the above expression:
. Finally, substituting this into the above expression:

since partials commute.
Levi-Civita connection
Let 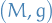 be a psuedo-Riemannian manifold. There exist a unique connection
be a psuedo-Riemannian manifold. There exist a unique connection  with vanishing torsion and satisfying
with vanishing torsion and satisfying  .
.
This choice of connection is often called the Levi-Civita connection.
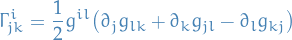
Curvature of Levi-Civita connection
Let  be the Levi-Civita connection. We define the (0, 4)-tensor
be the Levi-Civita connection. We define the (0, 4)-tensor


We work in normal coordinates at  , so
, so

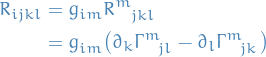
and so
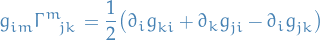
(at  ) differentiate wrt.
) differentiate wrt.  and evaluate at
and evaluate at 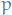 :
:
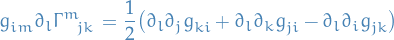
at 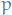 .
.
AND MORE.

for Levi-Civita connection.
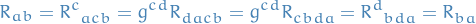
using Proposition proposition:4.61-lectures.
The Ricci scalar of 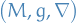 is
is

The Einstein tensor


Riemann tensor of 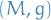 vanishes if and only if for every
vanishes if and only if for every  , there exists a chart containing
, there exists a chart containing 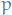 such that
such that

Recall if torsion vanishes, then Riemann tensor vanishes if and only if there exists charts where  . Then
. Then

in such charts.
This implies that  is constant in chart, if we choose basis at
is constant in chart, if we choose basis at 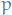 to be orthonormal, which implies
to be orthonormal, which implies

Theorem thm:Riemann-tensor-vanish-iff-Euclidean-or-Minkowski-metric shows us that the Riemann tensor sort of measure the deviation from Euclidean or Minkowski metric, locally.
Weyl tensor
- Ricci tensor and Ricci scalar contain information about "traces" of the Riemann tensor
- Sometimes useful to consider separately those parts of the Riemann tensor
 which the Ricci tensor
which the Ricci tensor  does not tell us about
does not tell us about
The Weyl tensor is defined (in  dimensions)
dimensions)
![\begin{equation*}
\tensor{C}{^{}_{abcd}} = \tensor{R}{^{}_{abcd}} - \frac{2}{(n - 2)} \big( \tensor{g}{^{}_{a [c}} \tensor{R}{^{}_{d] a}} - \tensor{g}{^{}_{b [c}} \tensor{R}{^{}_{d] a}} \big) + \frac{2}{(n - 1)(n - 2)} R \tensor{g}{^{}_{a[c}} \tensor{g}{^{}_{d]c}}
\end{equation*}](../../assets/latex/general_relativity_dd2fc54c0d56de307e015518185587e2553e3ef3.png)
The Weyl tensor is basically the Riemann tensor with all of its contractions removed. The above formula is designed so that all possible contractions of  vanish, while it retains the symmetries of the Riemann tensor:
vanish, while it retains the symmetries of the Riemann tensor:
![\begin{equation*}
\begin{split}
C_{abcd} &= C_{[ab][cd]} \\
C_{abcd} &= C_{cd ab} \\
C_{a [bcd]} &= 0
\end{split}
\end{equation*}](../../assets/latex/general_relativity_51bec12508fef6c7284ea63804215a4ab9dc1fb5.png)
One of the most important properties of the Weyl tensor is that it's invariant under
Special relativity
Spacetime is just a Lorentizan manifold 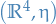 (Minkowski spacetime),
(Minkowski spacetime),
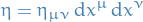
where

and 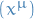 are the inertial coordinates, i.e.
are the inertial coordinates, i.e. 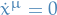 .
.
Free motion: are timelike geodesics, ligthrays null geodesics
Physics: described by tensor fields on 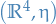 which obey evolution equations.
which obey evolution equations.
Examples
Scalar field
Let  be a scalar field, then
be a scalar field, then

which is just the wave-equation:
![\begin{equation*}
\bigg( - \pdv[2]{}{(x^0)} + \pdv[2]{}{(x^1)} + \dots \bigg) \Phi = 0
\end{equation*}](../../assets/latex/general_relativity_0733cbc9fb09fb947c3e6f329bc56b6e14333f31.png)
Energy-momentum tensor
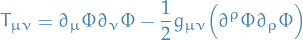
satisfies

which is conservation of energy / momentum.
Maxwell's theory of E. M.
Electromagnetic field strength
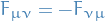 which obeys the Maxwell's equations:
which obeys the Maxwell's equations:
![\begin{equation*}
\tensor{\eta}{^{\mu \nu}_{}} \partial_{\mu} \tensor{F}{^{}_{\nu \rho}} = 0 \quad \text{and} \quad \partial_{[\mu} F_{\nu\ rho]} = 0
\end{equation*}](../../assets/latex/general_relativity_296481eddd2612a9d0b5c81001b1ce69d069d080.png)
The corresponding energy-momentum tensor
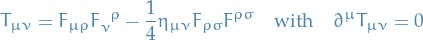
Any matter distribution is described by energy-momentum tensor

Fluids
- Described by vector field
 , and typically normalized such that
, and typically normalized such that 
Perfect fluids:

where
 is the energy density
is the energy density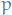 is the pressure
is the pressure
- Then
 is the relativitic eqns. of fluid dynamics
is the relativitic eqns. of fluid dynamics
General relativity
Main idea: there exist local freely flowing frames with no gravity.
This is achieved by the following postulates.
Postulates:
- Space-time is a 4D Lorentzian manifold
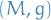
- Free particles follow timelike / null-geodesics wrt. Levi-Civita of
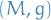
Energy-momentum distribution of matter fields described by
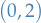 symmetric tensor field
symmetric tensor field  which is conserved
which is conserved

The curvature of
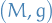 is related to energy-momentum tensor of matter by the Einstein's equations:
is related to energy-momentum tensor of matter by the Einstein's equations:

where
 is the Newton gravitational constant.
is the Newton gravitational constant.
- Note that
 might also depend on
might also depend on  , so we cannot simply fix
, so we cannot simply fix  and solve
and solve
- Note that
Laws of physics governed by:
- General covariance: laws indep. of basis / coord system
- Equivalence principle: in any local inertial frame (normal coordinate system) laws reduce to the laws in Minkowski spacetime (Minkowski space)
Do not fix laws uniquely! But suggests simple rule (called minimal coupling):
given any equation in
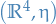 (Minkowski space), we replace
(Minkowski space), we replace
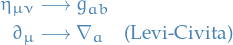
to get laws on curved spacetime
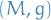
- Rules ensure general covariance as they output tensor equations.
Local intertial frames are normal coords at
 , i.e.
, i.e.

Examples
Wave equation
Applying these rules to wave-equation of S.R. we get

In local inertial frame, observe that we have

where the RHS is the wave-equation in 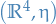 .
.
Postulate 3: we have
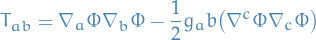
and by wave-equation

Maxwell's equations
Applying these rules to Maxwell's equations in spacetime, we get
![\begin{equation*}
g^{ab} \nabla_a F_{bc} = 0 \quad \text{and} \quad \nabla_{[a} F_{bc]} = 0 \quad \text{and} \quad F_{ab} = - F_{ba}
\end{equation*}](../../assets/latex/general_relativity_fca23535160470786383a90a0d3f4178e4497eaf.png)
Postulate 3: we have

combined with Maxwell's equations we get

Fluids
- Described by vector field
 , and typically normalized such that
, and typically normalized such that 
Perfect fluids:

where
 is the energy density
is the energy density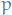 is the pressure
is the pressure
Then
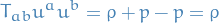
Motion of fluid given by
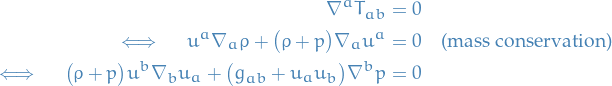
Observe that if the pressure vanish, i.e. 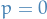 , then we're left with
, then we're left with

which is the equation describing geodesic, fluid moves as "free particles".
Einstein's equations
- Motivation:
- Newtonian
- Graviational field described by scalar potential

Equation of motion
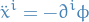
where
 in cartesian coordinates
in cartesian coordinates
Relative acceleration of nearby particles ("tildal force") governed by deviation equation

where
 is the separation vector of the particles
is the separation vector of the particles
- Graviational field described by scalar potential
- GR:
Relative acceleration of two nearby particles following timelike geodesics is given by the geodesic deviation equation
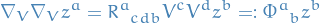
where
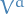 is the tangent to the geodesics and
is the tangent to the geodesics and 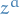 is now the deviation vector.
is now the deviation vector.
Comparison suggests

- Newtonian
Spacetimes
(anti-)de Sitter
de Sitter spacetime in  dimensions with radius of curvature
dimensions with radius of curvature  is locally isometric to the quadratic
is locally isometric to the quadratic

Anti de Sitter spacetime in  dimensions with radius of curvature
dimensions with radius of curvature  is locally isometric to the quadrics
is locally isometric to the quadrics

More precisely, the de Sitter spacetimes are the simply-connected universal covers of these quadrics.
Taking the limit  is equivalent to the zero curvature limit in which we recover Minkowski spacetime.
is equivalent to the zero curvature limit in which we recover Minkowski spacetime.
The real affince space  with a metric which, when expressed relative to affine coordinates, is given by
with a metric which, when expressed relative to affine coordinates, is given by
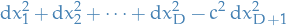
where we have introduced the speed of light  .
.
We may take limits:
- non-relativistic limit (on the co-metric):
 gives us galilean spacetime
gives us galilean spacetime - ultra-relativistic limit (on the co-metric):
 gives us carrollian spacetime
gives us carrollian spacetime
These spacetimes are no longer lorentzian: the (co-)metric becomes degenerate in the limit, leading to a galilean and a carrollian structure, respectively.
 tensor defined by contraction of the
tensor defined by contraction of the 

![\begin{equation*}
\nabla_{[c} \tensor{R}{^{a}_{|b|de]}} = 0
\end{equation*}](../../assets/latex/general_relativity_bf72beb7eab9dbc9f36a1d673062b7602cb92dc4.png)

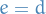

 , noting that
, noting that  by
by 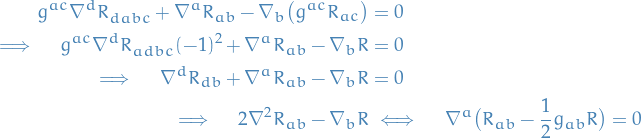

 since
since  .
.