Gauge Theory

Table of Contents

Mathematical formalism

Gauge theory involves a fibre bundle in which the fibre at each point, $F_p$, of the base space $E$ consists of possible coordinate bases for use when describing the values of the objects at that point.

One chooses a particular coordinate basis at each point (a local section of the fibre bundle), and express the values of the objects of the theory (usually "fields" in the physicst's sense) using this basis.

Two such configurations are equivalent if they are related by a transformation of this abstract coordinate basis (a change of local section, or a gauge transformation).

A gauge is just a choice of (local) section of some principal bundle.

A gauge transformation is just a transformation between two such sections / "choices".

What is gauge? - Terry Tao

Notation

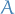  • coordinate system $\Phi: A \to G$ identifies some geometric object $A$ with standard object $G$
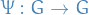  • $\Psi: G \to G$ is an isomorphism of that standard object
  • new coordinate system $\Psi \circ \Phi: A \to G$
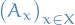  • $\big( A_x \big)_{x \in X}$ is a family (fibre bundle) of geometric (or combinatorial) objects (fibres) parametrized by some base point $x \in X$, where $X$ is the base space

Definitions

A homogenous space for a group $G$ is a non-empty manifold or topological space $X$ on which $G$ acts transitively.

The elements of $G$ are called the symmetries of $X$.

In physics, gauge fixing (also called choice of gauge) denotes a procedure for coping with redundant degrees of freedom in field variables.

A gauge theory represents each physically distinct configuration of the system as an equivalence class of detailed local field configurations.

Any two detailed configurations in the same equivalence class are related by a gauge transformation.

Stuff

Gauge
"coordinate system" that varies depending on one's "location" wrt. some base space or "parameter space"
Gauge transform
change of coordinates applied to each such location
Gauge theory
model for some physical or mathematical system to which gauge transforms can be applied (and is typically gauge invariant, in that all physically meaningful quantities are left unchanged under gauge transformations)
(no term)
Dimensional analysis is nothing more than the analysis of the scaling symmetries in one's coordinate systems.
(no term)
Consider general case where we have a family (or fibre bundle) of geometric (or combinatorial) objects (or fibres) parametrised by some base point $x \in X$

Examples

Circle bundle of the sphere

  • Space of directions in a plane $\mathbb{R}^2$ (which can be viewed as the circle of unit vectors) can be identified with the standard circle $S^1$ after picking:
    • orientation
    • reference direction
  • Consider the sphere instead on the surface $X$ of the earth
  • Each point $x \in X$ on surface, there is a circle $S_x$ of directions that one can travel along

  • Defines the collection

    \begin{equation*} SX := \big( S_x \big)_{x \in X} \end{equation*}

    of all such circles is then a circle bundle with base space $X$ (know as the circle bundle)

  • Structure group of this bundle is the circle group

    \begin{equation*} U(1) = S^1 \end{equation*}

    if one preserves orientation

  • Suppose every point $x$ on the earth $X$, we have wind $w_x \in S_x$ (ignoring the hairy ball theorem)
  • Wind direction is collection $w = \big( w_x \big)_{x \in X}$ of representatives from the fibres of teh fibre bundle $\big( S_x \big)_{x \in X}$
    • Such a collection is known as a section of the fibre fundle

  • Can define function

    \begin{equation*} u: X \to S^1 \end{equation*}

    i.e. a function which "converts" the collection of winds $w$ into points on the earth

    • Requires choosing a gauge for this circle bundle, i.e. selecting orientation 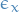$\epsilon_x$ and reference direction $N_x$ for each point $x \in X$
  • Thus, we have numerical representation of the "winds", which allows usage of analytical tools (e.g. differentiation, integration, Fourier transforms, etc.)

Orienting / directing an undirected graph

  • Undirected graph $G = (V, E)$ with $V$ being the space of vertices and $E$ the space of edges
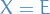  • $X = E$ (not the space of vertices!)
  • $e \in X$ can be oriented / directed in two different ways; let $A_e$ be the pair of directed edges of $e$ arising in this manner
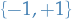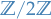  • $\big( A_e \big)_{e \in X}$ is a fibre bundle with base space $X$ and with each fibre isomorphic to the standard two-element set $\{ -1, +1 \}$ with structure group $\mathbb{Z} / 2 \mathbb{Z}$.

  • We can choose orientations for each edge, thus creating a gauge (or a section)

    \begin{equation*} \big( \vec{e} \big)_{e \in X}$ \end{equation*}

    of the bundle $\big( A_e \big)_{e \in X}$

  • Identify the bundle $\big( A_e \big)_{e \in X}$ with the trivial bundle $X \times \left\{ -1, +1 \right\}$:
    • preferred oriented edge 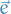$\vec{e}$ (or preferred orientation) of each $e \in X$ is assigned $(e, +1)$
    • other oriented edge of $e \in X$ is assigned $(e, -1)$