Fields

Table of Contents

Equations / Laws

Coulomb's Law

\begin{equation*} \mathbf{F} = \frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2} \hat{\mathbf{r}} \end{equation*} 1

where permittivity constant of free space $\varepsilon_0 = 8.85418 * 10^{-12} C^2 N^{-1} m^{-2}$

Electric Field

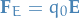
\begin{equation*} \mathbf{F}_E = q_0 \mathbf{E} \end{equation*}

where $q_0$ is the test charge, $\mathbf{E}$ is the electric field at that point.

Magnetic Field

\begin{equation*} \mathbf{F}_B = q \big( \mathbf{v} \times \mathbf{B} \big) \end{equation*}

Lorentz Force

This is just writing the magnetic and electric in a single equation.

\begin{equation*} \mathbf{F} = q \big( \mathbf{E} + \mathbf{v} \times \mathbf{B} \big) \end{equation*}

Electric Flux

\begin{equation*} \Phi_E = \mathbf{E} \cdot \mathbf{A} \end{equation*}

Gauss's Law

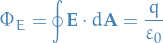
\begin{equation*} \Phi_E = \oint \mathbf{E} \cdot d\mathbf{A} = \frac{q}{\varepsilon_0} \end{equation*}

for Gaussian surfaces, i.e. general closed surface with all surface elements pointing outwards.

Potential Difference as work

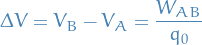
\begin{equation*} \Delta V = V_B - V_A = \frac{W_{AB}}{q_0} \end{equation*}

I.e. potential-difference is simply work used on a test-charge.

Potential Energy

\begin{equation*} U = q_0 V \end{equation*}

Potential

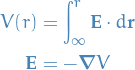
\begin{equation*} \begin{split} V(r) &= \int_\infty^r \mathbf{E} \cdot d \mathbf{r} \\ \mathbf{E} &= - \boldsymbol{\nabla} V \end{split} \end{equation*}

Ampere's Law

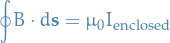
\begin{equation*} \oint B \cdot d \mathbf{s} = \mu_0 I_{\text{enclosed}} \end{equation*}

Biot-Savarts

\begin{equation*} d \mathbf{B} = \frac{\mu_0 I}{4 \pi} \frac{d \mathbf{s} \times \hat{\mathbf{r}}}{r^2} \end{equation*}

where $d \mathbf{s}$ is the vector whose magnitude is the length of the differential element of the wire in the direction of conventional current.

Thus, $d \mathbf{B}$ is tangential to the surface of the wire, perpendicular to the current-flow (following the right-hand rule).

Dipole moment

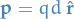\begin{equation*} \mathbf{p} = q d \ \hat{\mathbf{r}} \end{equation*} 2

where $d$ is the distance between charges and $\hat{\mathbf{r}}$ is the dipole axis.

Continuous Charge Distribution

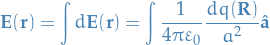
\begin{equation*} \mathbf{E}(\mathbf{r}) = \int d \mathbf{E}(\mathbf{r}) = \int \frac{1}{4 \pi \varepsilon_0} \frac{dq (\mathbf{R})}{a^2} \hat{\mathbf{a}} \end{equation*}

where $\mathbf{a} = \mathbf{r} - \mathbf{R}$

Torque

\begin{equation*} \boldsymbol{\tau} = \mathbf{p} \times \mathbf{E} \end{equation*}

Faraday's Law

Induced emf in a conducting loop is given by the rate of change of magnetic flux through the loop, i.e.

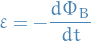
\begin{equation*} \varepsilon = - \frac{d \Phi_B}{dt} \end{equation*}

Lenz's Law

The induced current has a direction s.t. the magnetic field due to this current opposes the change in the magnetic field that caused it.

Capacitor

Charge stored

\begin{equation*} q = VC \end{equation*}

Impedence

Definitions

Electric dipole

Two charges of different charge separated by a fixed distance.

Examples

AC

Electromagnetic force $\varepsilon$ is given by:

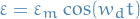
\begin{equation*} \varepsilon = \varepsilon_m \cos (w_d t) \end{equation*}

The resulting current is:

\begin{equation*} i = I \cos (w_d t - \phi) \end{equation*}

where $\phi$ is the phase-difference between $\varepsilon$ and $i$.

How-to

  1. Setup the differential equation for charge wrt. time, using Kirchoff's Law and the fact that the potential difference across all components need to sum to the potential difference across the entire circuit.
  2. Solve said differential equations.

Capacitive load circuit

\begin{equation*} q_c = VC \implies q_c = C V_0 \cos (\omega_d t) \end{equation*}

Thus, "current" across the capacitor $i_c$

\begin{equation*} i_c = \frac{d q_c}{d t} = - C \varepsilon_m \omega_d \sin ( \omega_d t) \end{equation*}