Electrodynamics

Table of Contents

Equations / Theorems

Guass' Law for electrical field of closed surface

\begin{equation*} \Phi_E = \oint_A \mathbf{E} \cdot d\mathbf{S} = \frac{Q_\text{enc}}{\varepsilon_0} = \int_V \frac{\rho( \mathbf{r} )}{\varepsilon_0} dV \end{equation*}

for any closed surface 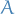$A$ and $\rho(\mathbf{r})$ is the surface charge-density.

Poisson's Equation

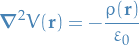
\begin{equation*} \boldsymbol{\nabla}^2 V(\mathbf{r}) = - \frac{\rho( \mathbf{r} )}{\varepsilon_0} \end{equation*}

where we've used Gauss' Law and the fact that 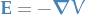$\mathbf{E} = - \boldsymbol{\nabla} V$.

Boundary conditions

We have the standard boundary conditions in Electrostatiscs:

\begin{equation*} V = 0 \quad \text{on conducting surface} \end{equation*}
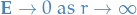
\begin{equation*} \mathbf{E} \to 0 \ \text{as} \ r \to \infty \end{equation*}

Note that since 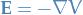$\mathbf{E} = - \nabla V$ we basically have boundary conditions for 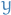$y$ and $y'$ in the "normal" ODE sense.

Properties

Uniqueness

The notes.

For any two different solutions of the Poisson's equation, the solutions only differ by a constant.

Laplace's equation

\begin{equation*} \boldsymbol{\nabla}^2 V(\mathbf{r}) = 0 \end{equation*}

which is a special case of the Poisson's Equation, where we have space absent of free charges .

Examples

Hollow conductor surface

The charge density within the follow region is $\rho = 0$, and thus we have the Laplace's equation with the boundary conditions $V(\mathbf{r}) = V_0$ where $V_0$, i.e. the potential at the boundary of the inner (non-charge) region is equal to the potential of the inner boundary of the conductor (since they're obviously the same boundary).

Method of Images

  1. "Imagine" a charge s.t. we get a homogenous PDE (equiv. Laplace's equation)
  2. Solve homogenous PDE / Laplacian using [BROKEN LINK: No match for fuzzy expression: *Laplace's%20equation%20in%20cylindrical%20coordinates], i.e. assume a solution of the form $V(\mathbf{r}) = X(x) Y(y) Z(z)$
  3. Then find a special solution to the non-homogenous PDE
  4. The linear combination of these two then form the general solution to the problem

There is one issue that one my bring up; is this solution unique? As it turns out, it is!

Maxwell's equations

  1. Gauss's law

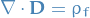
    \begin{equation*} \nabla \cdot \mathbf{D} = \rho_f \end{equation*}

  2. Guass's law for magnetism

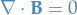
    \begin{equation*} \nabla \cdot \mathbf{B} = 0 \end{equation*}

  3. Maxwell-Faraday equation

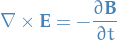
    \begin{equation*} \nabla \times \mathbf{E} = - \frac{\partial \mathbf{B}}{\partial t} \end{equation*}

  4. Ampère's circuital law

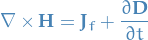
    \begin{equation*} \nabla \times \mathbf{H} = \mathbf{J}_f + \frac{\partial \mathbf{D}}{\partial t} \end{equation*}

where:

  • $\mathbf{D}$ is the displacement field, which accounts for the effect of free and bound charge within materials while its sources are the free charges only
  • $\mathbf{H}$ is the magnetizing field
  • $\mathbf{E}$ is the electric field
  • $\mathbf{B}$ is the magnetic field
  • $\rho_f$ is the free charge density