Angular Momentum

Table of Contents

Time derivatives in a rotating frame

Let $\hat{\mathbf{i}}$, $\hat{\mathbf{j}}$ and $\hat{\mathbf{k}}$ be unit basis vectors in the rotating frame, with a rotational speed of $\Omega$ about the axis $\boldsymbol{\Omega}$. Letting $\hat{\mathbf{u}}$ be the unit vector in this frame, we have:

\begin{equation*} \frac{d}{dt} \hat{\mathbf{u}} = \boldsymbol{\Omega} \times \hat{\mathbf{u}} \end{equation*}

Then if we have a function $\mathbf{f}$, taking the derivative in the rotational frame :

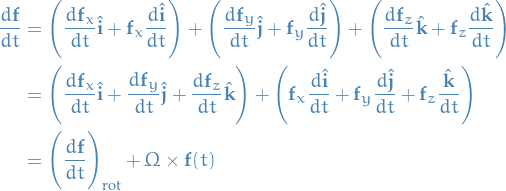
\begin{equation*} \begin{split} \frac{d \mathbf{f}}{dt} &= \Bigg( \frac{d \mathbf{f}_x}{dt} \hat{\mathbf{i}} + \mathbf{f}_x \frac{d \hat{\mathbf{i}}}{dt} \Bigg) + \Bigg( \frac{d \mathbf{f}_y}{dt} \hat{\mathbf{j}} + \mathbf{f}_y \frac{d \hat{\mathbf{j}}}{dt} \Bigg) + \Bigg( \frac{d \mathbf{f}_z}{dt} \hat{\mathbf{k}} + \mathbf{f}_z \frac{d \hat{\mathbf{k}}}{dt} \Bigg) \\ &= \Bigg( \frac{d \mathbf{f}_x}{dt} \hat{\mathbf{i}} + \frac{d \mathbf{f}_y}{dt} \hat{\mathbf{j}} + \frac{d \mathbf{f}_z}{dt} \hat{\mathbf{k}} \Bigg) + \Bigg( \mathbf{f}_x \frac{d \hat{\mathbf{i}}}{dt} + \mathbf{f}_y \frac{d \hat{\mathbf{j}}}{dt} + \mathbf{f}_z \frac{\hat{\mathbf{k}}}{dt} \Bigg) \\ &= \Bigg( \frac{d \mathbf{f}}{dt} \Bigg)_\text{rot} + \Omega \times \mathbf{f}(t) \end{split} \end{equation*}

Which describes the change of $\mathbf{f}$ wrt. $t$ using the rotational frame.

Euler's Equations (rigid body dynamics)

From Time derivatives in a rotating frame we have:

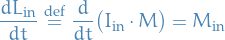
\begin{equation*} \frac{d L_\text{in}}{dt} \overset{\text{def}}{=} \frac{d}{dt} \big( I_\text{in} \cdot M \big) = M_\text{in} \end{equation*}

where $I_\text{in}$ is the moment of inertia tensor calculated in the intertial frame .

It's often more useful to change to coordinates to the rotating frame .

With rotating frame we mean that the coordinate axes are rotating about a fixed axis.

Why is this useful? In this frame the moment of inertia tensor is constant (and diagonal)!

Moment of inertia

Covariance and contravariance

  • Describe how the quantitive description of a certain geometric or physical entities change with a change of basis

Covariance

  • Components of a covector change in the same way as changes in scale of the reference axes → the covector and the reference axes are covariant

Contravariance

  • Components of a contr