String Theory

Table of Contents

Notation

  • Greek letters, e.g. $\alpha, \beta$, for variables or indices of variables
  • Std. leteters, e.g. 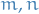$m, n$, for indices of target space
  • $\delta \sigma$ denotes how the Lagrangian changes wrt $\sigma$

Just notes

  • Gauge theories are used to obtain a "larger" space in which the symmetries (e.g. Lorentz invariance) becomes linear transforms

  • Start with action

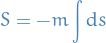
    \begin{equation*} S = -m \int \dd{s} \end{equation*}

    where $m$ is some constant (mass), and $\int \dd{s}$ is the arclength

  • Nambu-Goto action:

    \begin{equation*} S = - T \int \dd[2]{\sigma} \sqrt{- \det \gamma} \end{equation*}

    where

    \begin{equation*} \gamma_{\alpha \beta} = \partial_{\alpha} X^{m}(z, \sigma) \partial_{\beta} X^n(z, \sigma) \eta_{mn} \end{equation*}

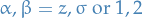    with $\alpha, \beta = z, \sigma \text{ or } 1, 2$, i.e. $\gamma$ a $2 \times 2$ matrix.

    • We are pulling back the metric of the target space
  • Symmetries
    • Gauge symmetries:

      • Reparametrizations $δ σα = - ζα(z, σ)

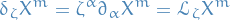
        \begin{equation*} \delta_{\zeta} X^m = \zeta^{\alpha} \partial_{\alpha} X^m = \mathcal{L}_{\zeta} X^m \end{equation*}

      • Std. parametrization:

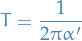
        \begin{equation*} T = \frac{1}{2 \pi \alpha'} \end{equation*}

        where $\alpha' = \ell_s^2$ is called the string length, and $T$ is called tension (energy of unit of length of the string)

    • Global symmetries:
      • $\delta X^m = a^m + \omega^{mn} X_n, \quad \omega^{mn} = - \omega^{nm}$ (where $\omega^{mn}$ are the Killing coefficients)

  • Polyakov action:

    \begin{equation*} S_p = - \frac{1}{4 \pi \alpha'} \int \dd[2]{\sigma} \sqrt{-h} h^{\alpha \beta} \big( \partial_{\alpha} X^m \partial_{\beta} X^n \eta_{mn} \big) \end{equation*}

    where

    \begin{equation*} h = \det \big( h_{\alpha \beta} \big) \end{equation*}

    and $h$ is a $2 \times 2$ symmetric metric.

    1. No kinetic term implies the equations of motion are 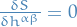$\frac{\delta S}{\delta h^{\alpha \beta}} = 0$, thus the symmetries become algebraic!

      • Note

        \begin{equation*} h_{\alpha \beta} = \big( f(z, \sigma) \big) \partial_{\alpha} X^m \partial_beta X^n \eta_{mn} \end{equation*}

        for some function $f$, which we can solve for if we know the action, but in general it can be any $f$, and so this is an example of a non-trivial Gauge symmetry

    2. Symmetries of $S_{p$
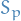
      1. Global: