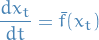Stochastic Approximation

Table of Contents

Overview

A simple goal: Find the solution $\theta^*$ to

\begin{equation*} \bar{f}(\theta^*) := \mathbb{E} \big[ f(\theta, W) \big] |_{\theta = \theta^*} = 0 \end{equation*}

Basic algorithm

\begin{equation*} \theta(n + 1) = \theta(n) + \alpha_n f \big( \theta(n), W(n + 1) \big) \end{equation*}

The stepsize satisfies:

  • Ensure we can reach anywhere: $\sum \alpha_n = \infty$
  • To attenuate noise: $\sum \alpha_n^2 < \infty$

Usually will take $\alpha_n = \frac{1}{n}$, which satisfies both of these.

Which we can write as:

\begin{equation*} \theta(n + 1) = \theta(n) + \alpha_n \big[ \bar{f} \big( \theta(n) \big) + \Delta (n + 1) \big] \end{equation*}

Which can be interpreted as a noisy Euler approximation to the ODE:

\begin{equation*} \frac{d x_t}{dt} = \bar{f}(x_t) \end{equation*}