Combinatorics
Let 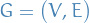 be a bipartite graph with partitions
be a bipartite graph with partitions 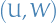 .
.
Suppose

where  .
.
Then, for non-empty $A ⊂ U,

Equality holds iff  is (r, s)-regular and
is (r, s)-regular and  .
.
Let $$$ be the subgraph induced by  , then
, then

where  is the number of edges in
is the number of edges in
Let 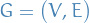 be a bipartite graph with partitions
be a bipartite graph with partitions 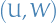 .
.
Suppose

where  .
.
Then, for non-empty $A ⊂ U,

Equality holds iff  is (r, s)-regular and
is (r, s)-regular and  .
.
Let $$$ be the subgraph induced by  , then
, then

where  is the number of edges in
is the number of edges in