Category Theory
Table of Contents
MEGA resource:
Notation
Definition
A category  consists of the three mathematical entities:
consists of the three mathematical entities:
- A class
 , whose elements are the objects
, whose elements are the objects - A class
 , whose elements are called morphisms or maps or arrows.
Each morphism
, whose elements are called morphisms or maps or arrows.
Each morphism  has a source object
has a source object 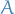 and target object
and target object 
A binary operation
 , called composition of morphisms, such that for any three objects
, called composition of morphisms, such that for any three objects 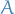 ,
,  , and
, and  , we have
, we have

The composition of
 and
and  is governed by two axioms:
is governed by two axioms:
Associativity:

Identity map:
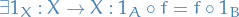
Category of Sets
The category  of
of  for any partially ordered set
for any partially ordered set  , where
, where
- a
 is a function
is a function  from a set
from a set  to
to 
a morphism
 of
of 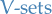
 and
and 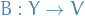 is a function
is a function
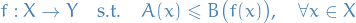
Let  , i.e.
, i.e. 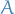 be the singleton set, then, for any set
be the singleton set, then, for any set  there is an isomorphism of sets
there is an isomorphism of sets

Just to make the point clear here, for the set  ,
,  where
where  is defined by the mapping:
is defined by the mapping:

Products
Let  and
and  be sets.
be sets.
The product of  and
and  , denoted
, denoted  , is defined as the set of ordered pairs
, is defined as the set of ordered pairs  where
where  and
and  . That is,
. That is,
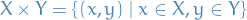
There are two natural projections 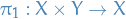 and
and  .
.
Let  and
and  be sets.
be sets.
For any set 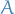 and functions
and functions  and
and  there exist a unique function
there exist a unique function  such that the following diagram commutes:
such that the following diagram commutes:
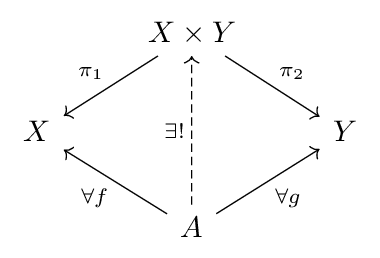
We might write the unique function as

Suppose we are given 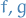 as above. To provide a function
as above. To provide a function  is equivalent of providing an element
is equivalent of providing an element  for each
for each  .
.
We need such a function  for which
for which

An element of  is an ordered pair
is an ordered pair  , and so we can use
, and so we can use

Hence, it's necessary and sufficient to define

Coproducts
Let  and
and  be sets.
be sets.
The coproduct of  and
and  , denoted
, denoted 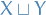 is defined as the disjoint union of
is defined as the disjoint union of  and
and  , i.e. the set for which an element is either an element of
, i.e. the set for which an element is either an element of  or an element of
or an element of  .
.
If something is an element of both  and
and  then we include both copies, and distinguish between them, in
then we include both copies, and distinguish between them, in  .
.
There are two natural inclusion functions

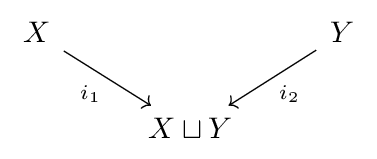
Finite limits in Set
Pullbacks
Suppose the given diagram of sets and functions below
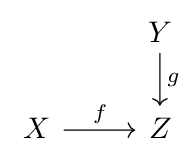
Its fiber product is the set

There are obvious projections

Note that if
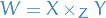
then the diagram
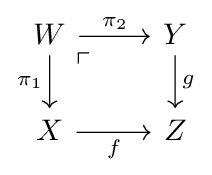 commutes.
commutes.
Given the setup in the diagram above, we define the pullback of  and
and  over
over  to be any set
to be any set  for which we have an isomorphism
for which we have an isomorphism
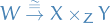
The corner symbol denotes that 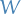 is the pullback.
is the pullback.
Sometimes you'll see the fiber product 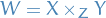 denoted
denoted  .
.
Suppose given the diagram of sets and functions as below.
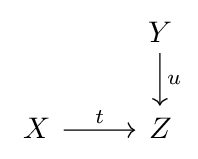
For any set 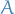 and commutative solid arrow diagram as below (i.e. functions
and commutative solid arrow diagram as below (i.e. functions  and
and  such that
such that 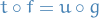 ),
),
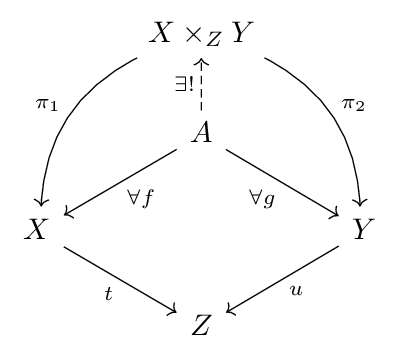
there exists a unique arrow  making everything commmute,
making everything commmute,

Category of Fuzzy Sets
The category of fuzzy subsets is denoted
![\begin{equation*}
\mathscr{F} = \text{Set}([0, 1])
\end{equation*}](../../assets/latex/category_theory_ea5d3d2c189416a415f2785697926cc619b7894a.png)
The objects of  are all pairs
are all pairs  where
where
 is a set
is a set![$A: X \to [0, 1]$](../../assets/latex/category_theory_6f2442223362e18297d22c1c9c79632210c5c1e2.png) is a function from
is a function from  to the unit interval
to the unit interval
The maps of  are defined by
are defined by

where  denotes the category of sets.
denotes the category of sets.
- With composition simply being the composition of functions
Course
Notation
- morphism is a structure-preserving map
Lecture 1
A category  consists of
consists of
- A collection
 of objects
of objects 
- A collection
 of morphisms
of morphisms 
- Two operations
 and
and  from
from  to
to  : we write
: we write  for "
for " and
and  and
and  ".
". - An operation
 from
from  to
to  , s.t.
, s.t. 
- A partial binary operation
 on
on  , defined iff
, defined iff 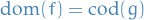 , and satisfying
, and satisfying  ,
,  .
. Satisfying

 whenever it makes sense (i.e. domain- and co-domain-conditions in (3) are satisfied)
whenever it makes sense (i.e. domain- and co-domain-conditions in (3) are satisfied)
- We don't require
 and
and  to be sets
to be sets
- If they are sets, we call
 small
small
- If they are sets, we call
- Could formualte the definition with "morphism" as the only primitive notion, identifying "objects"
 with identity morphisms.
with identity morphisms.
- However, in practice the objects are often logically prior to the morphisms
Examples
- The category
 has all sets as objects, and all functions between them as morphisms.
has all sets as objects, and all functions between them as morphisms.
- Formally, morphisms are pairs
 where
where  is a set-theoretic function and
is a set-theoretic function and 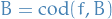
- Formally, morphisms are pairs
- Algebraic ones:
 is the category of groups and group homomorphisms
is the category of groups and group homomorphisms is the category of rings and ring homomorphisms
is the category of rings and ring homomorphisms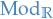 is the category of R-modules and R-module homomorphisms, for a particular ring
is the category of R-modules and R-module homomorphisms, for a particular ring 
- Topological:
 is the category of topological spaces with continuous maps as morphisms
is the category of topological spaces with continuous maps as morphisms is the category of smooth manifolds and
is the category of smooth manifolds and  maps as morphisms
maps as morphisms
- The category
 has the same objects as
has the same objects as  , but morphisms are homotopy classes of continuous maps.
, but morphisms are homotopy classes of continuous maps.
More generally, given an equivalence relation
 on
on  s.t.
s.t.
 implies
implies 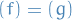 and
and 
 implies
implies  and
and  whenever the composites are defined
whenever the composites are defined
we have a new category
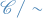 with the same objects as
with the same objects as  but
but  equivalence classes as morphisms
equivalence classes as morphisms
The category of relations,
 , has the same objects as
, has the same objects as  , but morphisms
, but morphisms  are relations
are relations  with composition of
with composition of  defined to be
defined to be
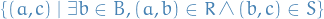
- The category
 also has sets as objects, but morphisms are partial functions, i.e. functions
also has sets as objects, but morphisms are partial functions, i.e. functions  for some
for some 
- The category
- For any category
 , the opposite category
, the opposite category  has the same objects and morphisms as
has the same objects and morphisms as  , but the
, but the  and
and  are interchanged, and thus the order of composition has to be interchanged, i.e.
are interchanged, and thus the order of composition has to be interchanged, i.e.  in
in  is
is  in
in  .
.
- Hence we have the duality principle: if
 is a true statement about categories, then so is the statement I get by reversing all the arrows, denoted
is a true statement about categories, then so is the statement I get by reversing all the arrows, denoted  .
.
- Hence we have the duality principle: if
- A category with a single object
 has
has  for all morphisms
for all morphisms  , and so composition is defined everywhere.
Hence a samll category with one object may be "identified" with a monoid (i.e. a semigroup with 1)
, and so composition is defined everywhere.
Hence a samll category with one object may be "identified" with a monoid (i.e. a semigroup with 1)
- In particular, a group is a small category with one object in which all morphisms are isomorphisms.
- A (Brandt) groupoid is a category in which all morphisms as isomorphisms.
- E.g. for any category
 ,
,  has the same objects as
has the same objects as  , but only the isomorphisms of
, but only the isomorphisms of  as morphisms
as morphisms - Also, for any topological space
 , the fundamental groupoid
, the fundamental groupoid  has points of
has points of  as objects and morephisms
as objects and morephisms  are (homotopy classes of) paths
are (homotopy classes of) paths ![$u: [0, 1] \to X$](../../assets/latex/category_theory_7ec8a78902f620a393bf3e19286f6ee2259f2124.png) with
with  and
and 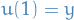 .
.
Composition: if
 , then
, then
![\begin{equation*}
[v] [u] = [u \cdot v]
\end{equation*}](../../assets/latex/category_theory_6cd53f236bddfa49a584a9e7e5d458f65b121092.png)
which is the same concatenation as used in homotopy equivalence.
- E.g. for any category