Search
Table of Contents
Definitions
Minimax
Minimax is a decision rule used for minimizing the possible loss of the worst case (maximum loss) scenario.
Tree search
alpha-beta pruning
Alpha-beta pruning is a search algorithm that seeks to decrease the number of nodes that are evaluated by the minimax algorithm in its search tree.
It stops completely evaluating a move when at least one possibility has been found that proves the move to be worse than a previously examined move. Such moves need not to be evaluated further. When applied to a standard minimax tree, it returns the same move as minimax would, but prunes away branches that cannot possibly influence the final decision.
It is an adverserial search algorithm.
Psuedo-code
def alpha_beta(node, depth, alpha, beta, is_maximizing_player): if depth == 0 or node.is_terminal_node: return node if is_maximizing_player: v = - np.inf for child in node.children: v = max(v, alpha_beta(child, depth - 1, alpha, beta, False)) a = max(alpha, v) if beta <= alpha: break return v else: v = np.inf for child in node.children: v = min(v, alpha_beta(child, depth - 1, alpha, beta, True)) beta = min(beta, v) if beta <= alpha: break return v
Monte Carlo Tree Search (MCTS)
Overview
- Each node holds:
 - the number of times this game-state has been visited
- the number of times this game-state has been visited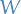 - the value of this game-state, which is computed by some function and the accumulated value of it's child-nodes
- the value of this game-state, which is computed by some function and the accumulated value of it's child-nodes

Algorithm
- Start at some root state
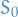
- Perform action
 to obtain the
to obtain the  "child-state"
"child-state" - Compute values
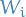 for each
for each  child
child - Update the parent state
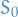 with the number of times we played in this state, i.e.
with the number of times we played in this state, i.e.  where
where  denotes the
denotes the  of the each of the child states
of the each of the child states - Unroll child-nodes in a smiliar way, always propagating the counts and values up the tree.
- When some terminating condition has been reached, choose the optimal child of the root state
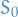 as the next move.
as the next move.