Maximum entropy models

Table of Contents

Notation

  • $\text{tr}(p)$ for a probability distribution denotes the integral over all inputs if continuous, and sum if discrete

Overview

  • MaxEnt models are models which attempts to maximize the information (Shannon) entropy wrt. constraints on statistics (e.g. first moment) of the "data" or underlying generating distribution

  • The optimization problem is then

    \begin{equation*} \begin{split} \max_{p} \quad & H[p] \\ \text{subject to } \quad \int p(\mathbf{x}) \dd{\mathbf{x}} = 1, \qquad & \int f_i(\mathbf{x}) p(\mathbf{x}) \dd{\mathbf{x}} = F_i, \quad i = 1, \dots, n \end{split} \end{equation*}

    where $f_i$ are arbitrary functions on the input-space, and $F_i$ are the values which the expectation of $f_i$ should take

  • Using Lagrange multipliers, we can write this as the minimization problem

    \begin{equation*} \begin{split} \mathcal{L}[p] =& - H[p] + \sum_{i}^{} \lambda_i \Bigg( \left\langle f_i \right\rangle_{\text{obs}} - \int f_i(\mathbf{x}) p(\mathbf{x}) \dd{\mathbf{x}} \Bigg) \\ &+ \gamma \Bigg( 1 - \int p(\mathbf{x}) \dd{\mathbf{x}} \Bigg) \end{split} \end{equation*}

    where we've chosen these arbitrary $F_i$ to be the observed expectations of $f_i$.

  • Solving for $p(\mathbf{x})$ by taking the functional derivative and setting to zero:

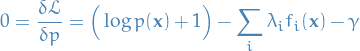
    \begin{equation*} 0 = \frac{\delta \mathcal{L}}{\delta p} = \Big( \log p(\mathbf{x}) + 1 \Big) - \sum_{i}^{} \lambda_i f_i(\mathbf{x}) - \gamma \end{equation*}

The general form of the maximum entropy distribution is then given by

\begin{equation*} p(\mathbf{x}) = \frac{1}{Z} \exp \bigg( \sum_{i}^{} \lambda_i f_i(\mathbf{x}) - \gamma \bigg) \end{equation*}

where

\begin{equation*} Z(\lambda_i) = \int \exp \bigg( \sum_{i}^{} \lambda_i f_i(\mathbf{x}) - \gamma \bigg) \dd{\mathbf{x}} \end{equation*}

Furthermore, the values of the Lagrange multipliers $\lambda_i$ are chosen to match the expectations of the functions $\{ f_i \}$, hence

\begin{equation*} \left\langle f_i \right\rangle_{\text{model}} = \int f_i(\mathbf{x}) p(\mathbf{x}) \dd{\mathbf{x}} = \frac{\partial Z}{\partial \lambda_i} = \left\langle f_i \right\rangle_{\text{obs}} \end{equation*}

i.e. the parameters of the distribution can be chosen s.t.

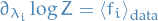
\begin{equation*} \partial_{\lambda_i} \log Z = \left\langle f_i \right\rangle_{\text{data}} \end{equation*}

Same holds for discrete random variables.

Still gotta estimate those moments yo!

Principle of Maximum Entropy

Shannon entropy

Say we want to define a function $I$ describing the information, in terms of an event $i$ with probability $p_i$; that is, how much information is acquired if we observe event $i$?

Such a function one would expect to have the following properties:

  1. $I(p)$ is monotonoically decreasing in $p$, i.e. if $p_i$ is large, then we gain little "information" by observing event $i$.
  2. $I(p) \ge 0$, i.e. "information" is a non-negative quantity.
  3. $I(1) = 0$, i.e. events occuring with a probability 1 provides no information.
  4. $I(p_i, p_j) = I(p_i) + I(p_j)$ for two independent events $i$ and $j$, i.e. the "joint information" of two independent random variables is the information of both added together.

It turns out that the following equation satisfies exactly these properties (see here for how to deduce it):

The average amount of information received for an event $i$ is given by

\begin{equation*} H(i) = - \sum_{i}^{} p_i \log p_i \end{equation*}

Justification

  • Consider discrete probability distribution among $m$ mutually exclusive propositions
  • Most informative distribution would occur when exactly one of the propositions was known to be true, in which case the information entropy would be zero (no "uncertainty").
  • Least informative distribution would occur when all propositions are equally likely (uniform), in which case the information entropy would be equal to its maximum possible value: $\log m$.
  • One can therefore view information entropy as a numerical measure of how uninformative a particular distribution is, ranging from zero to one.
  • Choosing a distribution with maximum entropy we are in a way choosing the most uninformative distribution possible, and to choose a distribution with lower entropy would be to assume information which is unknown.

Walllis derivation - combinatorial argument

  • https://en.wikipedia.org/wiki/Principle_of_maximum_entropy?oldformat=true#The_Wallis_derivation
  • Makes no reference to entropy as a measure of "uncertainty"
  • Want to make probability assignment to $m$ mutually exclusive propositions
  • Let 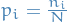$p_i = \frac{n_i}{N}$ be the probability of each of the $m$ propositions, with $n_i$ being the number of times the i-th proposition "occurs"

  • Probability of any particular results is the multinomial distribution:

    \begin{equation*} \text{Pr}(\mathbf{p}) = \frac{W}{m^N}, \quad W = \frac{N!}{n_1! n_2! \dots n_m!} \end{equation*}

  • Most probably results it the one which maximizes 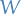$W$, equivalently, we can maximize any monotonic increasing function of $W$:

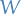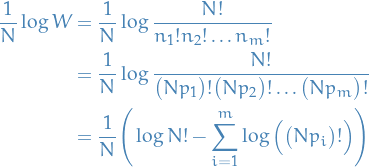
    \begin{equation*} \begin{split} \frac{1}{N} \log W &= \frac{1}{N} \log \frac{N!}{n_1! n_2! \dots n_m!} \\ &= \frac{1}{N} \log \frac{N!}{\big( N p_1 \big)! \big( N p_2 \big)! \dots \big( N p_m \big)!} \\ &= \frac{1}{N} \Bigg( \log N! - \sum_{i=1}^{m} \log \Big( \big( N p_i \big)! \Big) \Bigg) \end{split} \end{equation*}

  • Assuming $N \to \infty$ we have

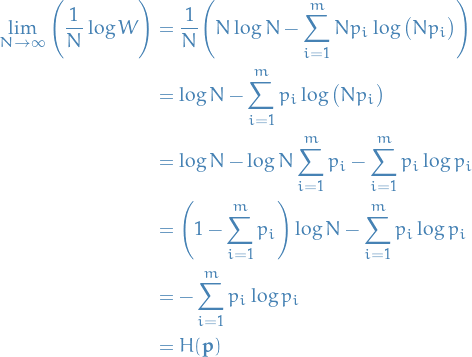
    \begin{equation*} \begin{split} \lim_{N \to \infty} \Bigg( \frac{1}{N} \log W \Bigg) &= \frac{1}{N} \Bigg( N \log N - \sum_{i=1}^{m} N p_i \log \big( N p_i \big) \Bigg) \\ &= \log N - \sum_{i=1}^{m} p_i \log \big( N p_i \big) \\ &= \log N - \log N \sum_{i=1}^{m} p_i - \sum_{i=1}^{m} p_i \log p_i \\ &= \Bigg( 1 - \sum_{i=1}^{m} p_i \Bigg) \log N - \sum_{i=1}^{m} p_i \log p_i \\ &= - \sum_{i=1}^{m} p_i \log p_i \\ &= H(\mathbf{p}) \end{split} \end{equation*}

Issues

  • Information about the probability distributions is intended to exist a priori
  • Information provided by measurements is only an estimate of "true" information, hence we require methods for entropy estimation.

Resources

Bibliography

Bibliography

  • [paninski_2003] Paninski, Estimation of Entropy and Mutual Information, Neural Computation, 15(6), 1191–1253 (2003). link. doi.