Kullback Leibler Divergence

Table of Contents

Definition

Let 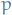$p$ and $q$ be two probability distributions for a random variable $X$.

The Kullback-Leibler (KL) divergence

  • if $X$ is discrete, is given by

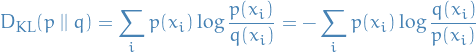
    \begin{equation*} D_{\rm{KL}}(p \ || \ q) = \sum_{i}^{} p(x_i) \log \frac{p(x_i)}{q(x_i)} = - \sum_{i}^{} p(x_i) \log \frac{q(x_i)}{p(x_i)} \end{equation*}

  • if $X$ is continuous,

    \begin{equation*} D_{\rm{KL}}(p \ || \ q) = \int p(x) \log \frac{p(x)}{q(x)} \dd{x} = - \int p(x) \log \frac{q(x)}{p(x)} \dd{x} \end{equation*}

Interpretation

Probability

Kullback-Leibner divergence from some probability-distributions $Q$ and $P$, denoted $D_{KL} (P || Q)$, is a measure of the information gained when one revises one's beliefs from the prior distribution $Q$ to the posterior distribution $P$. In other words, amount of information lost when $Q$ is used to approximate $P$.

Most importantly, the KL-divergence can be written

\begin{equation*} D_{\rm{KL}}(p \ || \ q) = \mathbb{E}_p\Bigg[\log \frac{p(x \mid \theta^*)}{q(x \mid \theta)} \Bigg] = \mathbb{E}_p \big[ \log p(x \mid \theta^*) \big] - \mathbb{E}_p \big[ \log q(x \mid \theta) \big] \end{equation*}

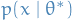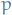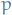where $\theta^*$ is the optimal parameter and $\theta$ is the one we vary to approximate $p(x \mid \theta^*)$. The second term in the equation above is the only one which depend on the "unknown" parameter $\theta$ ($\theta^*$ is fixed, since this is the parameter we assume $p$ to take on). Now, suppose we have $N$ samples $\{ x_i \}$ from $p$, then observe that the negative log-likelihood for some parametrizable distribution $q$ is given by

\begin{equation*} - \frac{1}{N} \sum_{i=1}^{N} \log q(x_i \mid \theta) \end{equation*}

By the Law of Large numbers, we have

\begin{equation*} \lim_{N \to \infty} - \frac{1}{N} \sum_{i=1}^{N} \log q(x_i \mid \theta) = - \mathbb{E}_p[\log q(x \mid \theta)] \end{equation*}

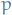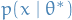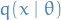where $\mathbb{E}_p$ denotes the expectation over the probability density $p$. But this is exactly the second term in the KL-divergence! Hence, minimizing the KL-divergence between $p(x \mid \theta^{\ast})$ and $q(x \mid \theta)$ is equivalent of minimizing the negative log-likeliood, or equivalently, maximizing the likelihood!

Coding

From Wikipedia:

The Kraft-McMillan theorem establishes than any decodable coding scheme for coding a message to identify one value $x_j$ out of a set of possibilities $X$ can be seen as representing an implicit probability distribution $q(x_j) = 2^{-l_j}$ over $X$, where $l_j$ is the length of the code for $x_j$ in bits

Therefore, we can interpret the Kullback-Leibner divergence as the expected extra message-length per datum that must be commincated if a code that is optimal for a given (wrong) distribution $Q$ is, compared to using a code based on the true distribution $P$.

Let's break this a bit down:

  • Kraft-McMillan theorem basically says when taking the exponential of the length of each valid "codeword", the resulting set (of exponentials) looks like a probability mass function.
  • If we were to create a coding schema for the values in $X$ (our set of symbols) using binary representation (bits) using our "suggested" probability distribution $Q$, KL-divergence gives us the expected extra message-length ber datum compared to using a code based on the true distribution $P$