Gaussian Processes

Results
Useful notes
- Hyperparameters tuning
IMPORTANT
Automatic Relevance Determination
Resources
Connection to RKHSs
- Connections between GPs and Kernel Ridge Regression

Results

Variational framework for learning inducing variables can be intepreted as minimizing a rigorously defined KL-divergence between the approximating and posterior processes. matthews15_spars_variat_method_kullb_leibl

Useful notes

Hyperparameters tuning

IMPORTANT

As of right now, must of the notes regarding this topic can be found in the notes for the book Guassian Proccesses for Machine Learning.

These will be moved in the future.

Automatic Relevance Determination

Consider the covariance function:

$\begin{equation*} \mathbf{K}_{nn'} = v \exp \Bigg[ - \frac{1}{2} \sum_{d=1}^D \Big( \frac{x_n^{(d)} - x_{n'}^{(d)}}{r_d} \Big)^2 \Bigg] \end{equation*}$ 1

The parameter $r_d$ is the length scale of the function along input dimension $d$ . This implies that as $r_d \rightarrow \infty$ the function $f$ varies less and less as a function $x^{(d)}$ , that is, the dth dimension becomes irrelevant.

Hence, given data, by learning the lengthscales $(r_1, \dots, r_D)$ is is possible to do automatic feature selection.

Resources

A Tutorial on Gaussian Processes (or why I don't use SVMs) by Zoubin Ghahramani A short presentation, providing an overview and showing how the objective function of a SVM is quite similar to a GP, but GP also has other nicer properties. He makes the following notes when comparing GPs with SVMs:
- GP incorporates uncertainty
- GP computes 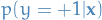$p(y = +1 | \mathbf{x})$ , not $p(y = +1| \hat{\mathbf{f}}, \mathbf{x})$ as SVM
- GP can learn the kernel parameters automatically from data, no matter how flexible we make the kernel
- GP can learn the regularization parameter $C$ without cross-validation
- Can combine automatic feature selection with learning using automatic relevance determination (ARD)

Connection to RKHSs

If both uses the same kernel, the posterior mean of a GP regression equals the estimator of kernel ridge regression

Connections between GPs and Kernel Ridge Regression

Notation

$\mathcal{X}$ non-empty set
$\mathfrak{f}: \mathcal{X} \to \mathbb{R}$ be a function
Given set of pairs $\left\{ (x_i, y_i) \right\}_{i = 1}^n \subseteq \mathcal{X} \times \mathbb{R}$ for $n \in \mathbb{N}$
Assumption/model:

$\begin{equation*} y_i = \mathfrak{f}(x_i) + \xi_i, \quad i = 1, \dots, n \end{equation*}$

where $\xi_i$ is a zero-mean rv. which represents "noise" or uncontrollable error
If 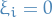$\xi_i = 0$ for all $i$ ,i .e. no output noise, then we call the problem interpolation
$X := \left\{ x_1, \dots, x_n \right\} \in \mathcal{X}^n$
$Y := \left\{ y_1, \dots, y_n \right\} \in \mathbb{R}^n$
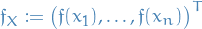$\mathfrak{f}_X := \big( \mathfrak{f}(x_1), \dots, \mathfrak{f}(x_n) \big)^T$ in the noise-free/interpolation case