Exercises

Table of Contents

Information Theory, Inference and Learning Algorithms

mackay2003information

6.14

Since there is no covariance between the different dimensions, i.e. the 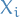$X_i$ are independent of all $X_j$ with $j \ne i$, we know that

\begin{equation*} \mathbb{E}[r^2] = \mathbb{E} \bigg[ \sum_{i=1}^{N} x_i^2 \bigg] = \sum_{i=1}^{N} \mathbb{E}[x_i^2] \end{equation*}

where each of the $x_i$ are following $x_i \sim \mathcal{N}(0, \sigma^2)$, hence

\begin{equation*} \mathbb{E} \big[ x_i^2 \big] = \text{Var}(x_i) - \big( \mathbb{E}[x_i] \big)^2 = \sigma^2 - 0 = \sigma^2 \end{equation*}

Hence,

\begin{equation*} \mathbb{E} \big[ r^2 \big] = \sum_{i=1}^{N} \sigma^2 = N \sigma^2 \end{equation*}

The variance is then given by

\begin{equation*} \text{Var}(r^2) = \mathbb{E} \big[ r^4 \big] - \Big( \mathbb{E} \big[ r^2 \big] \Big)^2 \end{equation*}

where

\begin{equation*} \mathbb{E} \big[ r^4 \big] = \mathbb{E} \Bigg[ \bigg( \sum_{i=1}^{N} x_i^2 \bigg)^2 \Bigg] = \sum_{i=1}^{N} \mathbb{E}\big[ x_i^4 \big] + \sum_{i \ne j}^{} \mathbb{E}\big[x_i^2 x_j^2 \big] \end{equation*}

But since there is no covariance between the different $x_i$, the second sum vanishes, and since

\begin{equation*} \mathbb{E} \big[ x_i^4 \big] = \int_{- \infty}^{\infty} x_i^4 \frac{1}{\sqrt{2 \pi} \sigma} \exp \bigg( \frac{x_i^2}{2 \sigma^2} \bigg) \ dx_i = 3 \sigma^4 \end{equation*}

(which we knew from the hint 6.14 in the book). Hence

\begin{equation*} \text{Var}(r^2) = \sum_{i=1}^{N} \mathbb{E} \Big[ x_i^4 \Big] - \big( \mathbb{E}[x_i^2] \big)^2 = \sum_{i=1}^{N} 3 \sigma^4 - \sigma^4 = 2 N \sigma^4 \end{equation*}

This all means that for large $N$, we will have

\begin{equation*} r^2 \approx N \sigma^2 \pm \sqrt{2 N} \sigma^2 \end{equation*}

And since 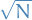$\sqrt{N}$ will be neglible for large $N$, compared to $N$ (of course assuming $\sigma$ is finite), then

\begin{equation*} r^2 \approx N \sigma^2 \implies r \approx \sqrt{N} \sigma \end{equation*}

as watned. The "thickness" will simply be the $2 \sqrt{2N} \sigma^2$, i.e. twice the variance of $r^2$.

Either by:

  • Computing an $N$ dimensional integral :)
  • Empirically looking at 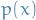$p(x)$ for some $x$ and making use of the symmetry of the Gaussian to infer that all $\mathbf{x}$ with same radius have the same probability, and that $p(\mathbf{x})$ decreases when $\mathbf{x}$ moves away (in whatever "direction" / dimension) from the mean

We can observe that the majority of the probability mass is clustered about this "shell".

Bibliography

Bibliography

  • [mackay2003information] MacKay, Kay & Cambridge University Press, Information Theory, Inference and Learning Algorithms, Cambridge University Press (2003).