Convolutional Neural Networks
Table of Contents
Overview
Hello my fellow two-legged creatures! Today we'll have a look at convolutional networks, and more specifically, how they really work.
I will start out with the very simplest case, and then generalize at the end.
Motivation
When I was trying to wrap my head this topic, I found some great lectures / tutorials, such as Hugo Larochelle's video series (his entire entire series on Neural Networks is amazing by the way, so do have a look!) and Andrew Gibiansky's blog post on the topic.
Now, both of these were really well-done and provided me with a lot insight, but at the time it had been a couple of months since I had been doing anything involving Neural Networks and I wasn't really familiar with the mathematical concept of "convolution". Therefore after watching / reading the above I felt as I understood what this was all about, but only on a very high-level; too high, after my taste. There we're small things that made it hard for me to really understand what was going on:
- Hugo does this pretty cool thing were he uses the same notation as they did in the first "major" paper describing the technique (2009, Jared et. al.). He does this in basically every video, and in general I think it's great! But despite his efforts to make it clear whenever he was redefining some notation (following the paper), I felt this made it slightly harder to follow.
- Hugo explains the intuition behind the convolution operation and states that we can view the operation we're interested in (I'll get to this) as taking the convolution between the input channel and the weight matrix with its axes flipped . That's cool and all, but I would really like to know why . By the way, for what Hugo is trying to do, I think he is absolutely correct in not digging into the convolution part. I also believe Hugo encouraged people to attempt to obtain the full expression for the backward pass in the forward-backward algorithm themselves. Again, I also believe you ought to try that first, but I figured I would provide my view on things in case you get stuck or want to confirm (I hope..) your own deduction.
- Andrew's post did go a bit more into the details of the forward-backward algorithm for a convolutional layer, but doesn't really show why we can view this as a convolution. Also, going from the notation used in Hugo's lectures to Andrew's blog post was a bit difficult.
In the end I was left with this nagging question:
Why the "convolution" in a convolutional network?!
Notation
One thing I found quite confusing when trying to understand convolutional networks myself, was the discrepancy in notation across different sources. Granted, one of the reasons why this is the case is because in a convolutional network there is a lot of different symbols to keep track of.
Because of this I now try to impose on you another notation! Now, this might seem a bit weird after what I just said, but it is due to the fact that I want to introduce this topic in a slightly more detailed manner than the other resources I found and instead trying to merge their notation, it's easier to simply create my own.
Firstly, the following schema will always be applicable unless specified otherwise:
If we are looking at some integers from some arbitrary number up to  ,
we will use the notation
,
we will use the notation  , i.e.
, i.e. 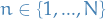 If multiple integeres from this set is required, we will use the
subscript to separate them, i.e.
If multiple integeres from this set is required, we will use the
subscript to separate them, i.e. 
More specifically, we will use the following notation:
 is the
is the  layer in network
layer in network is the entire input vector or matrix to the network itself, and we use
is the entire input vector or matrix to the network itself, and we use
 for the entire input vector or matrix to the
for the entire input vector or matrix to the  layer
layer is the weight-vector or -matrix, with
is the weight-vector or -matrix, with  being the one acting on the input
being the one acting on the input 
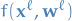 is the pre-activation, i.e. the input to the
activation / non-linear function
is the pre-activation, i.e. the input to the
activation / non-linear function 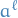
 is the entire output vector or matrix for the network itself, and we use
is the entire output vector or matrix for the network itself, and we use
 for the entire activation vector or matrix to the
for the entire activation vector or matrix to the  layer. That is,
layer. That is,

1D Convolutional Network
Notation
 denotes the
denotes the  entry in the weight-vector
entry in the weight-vector
2D Convolutional Network
Notation
 denotes the
denotes the  entry in the weight-matrix
entry in the weight-matrix