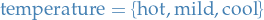CART: Classification & Regression Trees

Metrics

Metrics

Gini impurity

Measure of how often a randomly chosen element from the set would be incorrectly labeled if it was labeled randomly according to the distribution of the labels in the subset.

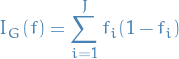$\begin{equation*} I_G (f) = \sum_{i=1}^{J} f_i (1 - f_i) \end{equation*}$ 1

Procedure

Draw random sample $x$ from the set (which in reality has label, say, $i$ )
Classify $x$ according to the distribution of the labels
Compute probability of misclassification, i.e. proportion of elements not labeled $i$
Compute Gini coefficient 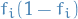$f_i (1 - f_i)$ , where $f_i$ is the proportion of label $i$ in the set
Perform step 1-4 for the child nodes (nodes after making some split)
Compare sum of coefficient for child nodes with parent node
Perform steps 1-6 for different features / independent variables / attributes to find the one with the best (i.e. smallest) coefficient and go ham (i.e. make a split).

Information gain

In information theory and machine learning: information gain is a synonym for the Kullback-Leibner divergence
In context of decision trees: sometimes used synonymously with mutual information, which is the expected value of the KL-divergence of the univariate probability distribution of one variable from the conditional distribution of this variable given the other one.

Notation

$T$ is the set of training examples
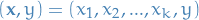$(\mathbf{x}, y) = (x_1, x_2, ..., x_k, y)$ is a training example
$x_a \in \text{vals}(a)$ is $a^{\text{th}}$ attribute
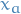$\text{vals}(a)$ is all possible value $x_a$ can take

Definition

$IG(T, a) = H(T) - H(T | a)$

$IG(T, a) = \text{entropy of parent} - \text{weighted sum of entropy of children}$

or best:

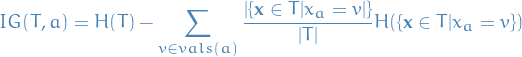$\begin{equation*} IG(T, a) = H(T) - \sum_{v \in vals(a)} \frac{|\{ \mathbf{x} \in T | x_a = v| \} }{|T|} H(\{\mathbf{x} \in T | x_a = v\}) \end{equation*}$ 2

which is just saying that Information Gain is the difference between the entropy for the entire training set and the weighted (by portion of samples which will fall into this node) sum of the entropy in the child-nodes.

Remember, Information Gain only makes sense when it comes to classification, not regression.

Difference between the entropy of a node $T$ and the sum of entropy of the children given that we decide to split on attribute $a$
We take the difference between uncertainty before and after the split, which gives us a measure of how much more certain we are by performing said split.
How much uncertainty we remove by making the split on this independent variable

Why the entropy?

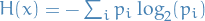
$H(x) = - \sum_i p_i \log_2 (p_i)$

$p_i$ is the probability of class $i$
Entropy is simply a function chosen to satisfy some criterias that one would intuitively want from a uncertainty-measure:
1. $H = 0 \implies \exists i | p_i = 1$
2. $\forall n \in \mathbb{N}$ , $H$ is maximum when $p_1 = ... = p_n$ , i.e. we are most uncertain when every possiblity is equally likely.
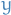3. $H(x, y) \leq H(x) + H(y)$ , with equality iff $x$ and $y$ are independent
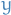4. $H(y) \geq H_x (y)$ , i.e. uncertainty regarding $y$ is never increased by knowing $x$
5. Any change towards equalization of the probabilities increases $H$ . Greater uncertainty ⇒ greater entropy.

Example

Consider an example data-set of 14 samples, with attributes:

$\text{outlook} = \{ \text{sunny}, \text{overcast}, \text{rainy} \}$
$\text{temperature} = \{\text{hot}, \text{mild}, \text{cool} \}$
$\text{humidity} = \{ \text{normal}, \text{high} \}$
$\text{windy} = \{ \text{true}, \text{false} \}$

And our (binary) dependent variable / output is $\text{play football} = \{ \text{true}, \text{false} \}$ .

Let's assume we make the first split on windy (in reality we would consider splitting on each of the independent variables and then use the one with the best metric), where the resulting tree has two nodes.

It keeps going here

Variance reduction

Often used when target is continuous (regression tree)
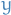Variance reduction of a node is the total reduction of the variance of the target variable $y$ due to the split at this node
- target variable 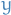$y$ being the value of the sample
look for the attribute / independent variable with the split "explaining" the most variance of our target variable 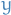$y$ , i.e. has the variance reduced the most

Defintion

$\begin{equation*} I_{V}(N)={\frac {1}{|S|^{2}}}\sum _{i\in S}\sum _{j\in S}{\frac {1}{2}}(x_{i}-x_{j})^{2}-\left({\frac {1}{|S_{t}|^{2}}}\sum _{i\in S_{t}}\sum _{j\in S_{t}}{\frac {1}{2}}(x_{i}-x_{j})^{2}+{\frac {1}{|S_{f}|^{2}}}\sum _{i\in S_{f}}\sum _{j\in S_{f}}{\frac {1}{2}}(x_{i}-x_{j})^{2}\right) \end{equation*}$ 3

where