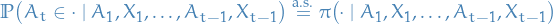Bandits
Table of Contents
Sequential decision problems
- Reward/feedback type:
- Bandit
- Only observe information/feedback for the action taken.
- Full information
- Observe information/feedback for all the actions.
- Partial information
- Observe information/feedback for a subset (potentially sparse) of possible actions.
- Bandit
Bandit book lattimore2018bandit
Notation
 denotes a stochastic bandit
denotes a stochastic bandit is the suboptimality gap or action gap or immediate regret of action
is the suboptimality gap or action gap or immediate regret of action 
Number of times action
 was chosen by the learner at the end of round
was chosen by the learner at the end of round 
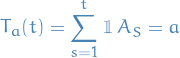
In general, this is random, since the action taken at time
 is a random variable depending on all previous observatiosn and actions.
is a random variable depending on all previous observatiosn and actions.
2
2.2 σ-algebras and knowledge
- Collection of sequential observations (rvs.)
- The set of maps
 such that
such that  is measurable then characterizes all the possible ways the learner can respond.
is measurable then characterizes all the possible ways the learner can respond.
- I.e. sufficies to concentrate on σ-algebra

- I.e. sufficies to concentrate on σ-algebra
- Reminder:
 is adapted to filtration
is adapted to filtration  if
if  is
is  for each
for each ![$t \in [n]$](../../assets/latex/bandits_77df7d259c970698dfceec77a36c5d52eec43d96.png) .
.
3
Markov Chains

4
4.5 Decomposing regret
For any policy 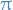 and stochastic bandit environment
and stochastic bandit environment  with
with  finite or countable and horizon
finite or countable and horizon  , the regret
, the regret  of policy
of policy 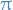 in
in  satisfies
satisfies
![\begin{equation*}
R_n = \sum_{a \in \mathcal{A}}^{} \Delta_a \mathbb{E} \big[ T_a(n) \big]
\end{equation*}](../../assets/latex/bandits_fffc6ec67a5bb6da46d3d3caae7a9dc5bc42573d.png)
5.
Exercises
5.3
Eq. (5.2):

Eq. (5.4):
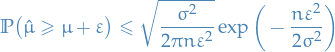
which means

Then the ratio between the two rates:
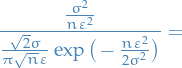
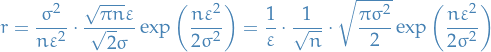
Then if  , we have
, we have  and
and  is dominated by
is dominated by 
Alternatively,
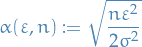
then

so,
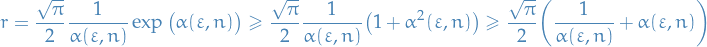
As a result, on  the lower-bound of the ratio is monotonically increasing in
the lower-bound of the ratio is monotonically increasing in  . On
. On  , the lower-bound of the ratio decreases monotonically in
, the lower-bound of the ratio decreases monotonically in  . For the increase, we can for certain say that
. For the increase, we can for certain say that
We know for  , the
, the  factor completely dominates. For
factor completely dominates. For  , we can use the fact that
, we can use the fact that
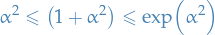
which means that
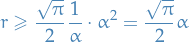
But for the question of when  , i.e. Eq. (5.2) is best, and
, i.e. Eq. (5.2) is best, and  , i.e. Eq. (5.4) is best, observe that if
, i.e. Eq. (5.4) is best, observe that if

which means Eq. (5.4) is best (BUT, 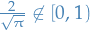 so it doesn't actually provide us with any more information!).
so it doesn't actually provide us with any more information!).
Moreover, in the case  , we know for certain that
, we know for certain that  and thus Eq. (5.4) is the best.
and thus Eq. (5.4) is the best.
We can refine our lower-bound of when  by using the slightly tighter lower-bound for
by using the slightly tighter lower-bound for  , where we have
, where we have
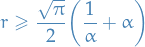
and we can solve for RHS = 1, or equiv.,
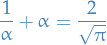
which is equivalent to the quadratic
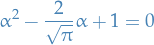
which has solutions
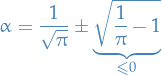
Therefore  has non-real imaginary component, i.e. this doesn't provide us with any more insight.
has non-real imaginary component, i.e. this doesn't provide us with any more insight.
But, we can consider when this quadratic is  and
and  which gives us
which gives us
6. The Explore-then-Commit Algorithm
Exercises
6.1 subGaussian empirical estimates
Let 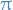 be the policy of ETC and
be the policy of ETC and  be the 1-subGaussian distributions associated with the
be the 1-subGaussian distributions associated with the  arms.
arms.
Provide a fully rigorous proof of the claim that

is  . You should only use the definitions and the interaction protocol, which states that
. You should only use the definitions and the interaction protocol, which states that
Recall that
The mean reward for arm
 is estimated as
is estimated as
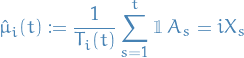
where
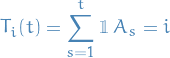
is the number of times action
 has been played after round
has been played after round  .
.
The ETC policy for parameter
 , which we denote
, which we denote  , is defined by
, is defined by
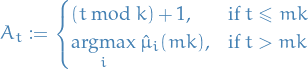
First we note that is sufficient to show that 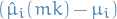 is
is  for all
for all  and that they're independent, since we can decompose the expression as:
and that they're independent, since we can decompose the expression as:

and by Lemma 5.4 (c) (which we need to prove!) a sum of two subGaussian rvs is a subGaussian [Easy to prove though (Y)]
[I guess we need the interaction protocol to actually prove that we can consider the mean-estimates as independent?]
7. The Upper Condience Bound (UCB) Algorithm
Notation
Optimism principle
11. The Exp3 Algorithm
Notation
Conditional expectation given history up to time

![\begin{equation*}
E_t \big[ \wc \big] = \mathbb{E} \big[ \wc \mid A_1, X_1, \dots, A_{t - 1}, X_{t - 1} \big]
\end{equation*}](../../assets/latex/bandits_65419dea819ca839a60d74491c76968d5880acc3.png)
IS estimator of
 is
is
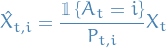
which satisfies
![\begin{equation*}
\mathbb{E}_t \big[ \hat{X}_{t, i} \big] = x_{t, i}
\end{equation*}](../../assets/latex/bandits_46ea048e1ee50e15245aa020ebfa980d67d9805f.png)
i.e. unbiased estimator. Note that in this case

Alternative (unbiased) estimator
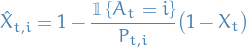
which is more easily seen by rearranging
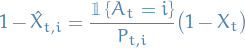
i.e. RHS is an estimate of the "loss"
 . Note that in this case
. Note that in this case
![\begin{equation*}
\hat{X}_{t, i} \in (-\infty, 1]
\end{equation*}](../../assets/latex/bandits_1b2fab581cb99f3c0a6eb96ae27c59d6a15de7d3.png)
Overview
- Adverserial bandits
11.3 The Exp3 algorithm
- Exp3 = Exponential-weight algorihtm for Exploration and Exploitation
- The idea is to construct unbiased estimators for the rewards from each arm by the use of IS.
Exp3 is a particular way of obtaining a distribution for each arm
 at time
at time  ,
,  :
:
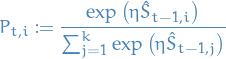
where
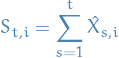
where
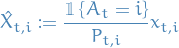
where
 is the reward at time-step
is the reward at time-step  chosen for arm
chosen for arm  by the adversary.
by the adversary.
 is referred to as the learning rate
is referred to as the learning rate
- In simple case will be chosen depending on number of arms
 and horizon
and horizon 
- In simple case will be chosen depending on number of arms
Let
![$x \in [0, 1]^{n \times k}$](../../assets/latex/bandits_0db521f5aa07e1b7146ac31f6ce53e70147c77d8.png)
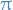 be the policy of
be the policy of Exp3with learning rate
Then
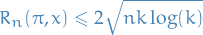
For any arm  define
define
![\begin{equation*}
R_{n, i} = \sum_{t = 1}^{n} x_{t, i} - \mathbb{E} \bigg[ \sum_{t = 1}^{n} X_t \bigg]
\end{equation*}](../../assets/latex/bandits_4e2a8f7e1755bc84bda1f4f77dab7dd6c0370fd0.png)
which is the expected regret relative to using action  in all the rounds.
in all the rounds.
We will bound  for all
for all  , including the optimal arm.
, including the optimal arm.
18. Contextual Bandits
For any ![$m^{\ast} \in [M]$](../../assets/latex/bandits_8a1a7713b40dfe3bfe2522906ea47276f7efb2aa.png) , it holds that
, it holds that
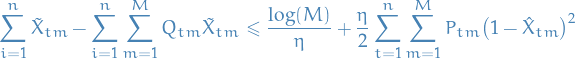
Recall that

i.e.
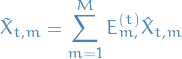
19. Linear Stochastic Bandits
19.3 Regret Analysis
Let  be positive definite and
be positive definite and  be a sequence of vectors with
be a sequence of vectors with  for all
for all ![$t \in [n]$](../../assets/latex/bandits_77df7d259c970698dfceec77a36c5d52eec43d96.png) .
.
Then

In the final inequality we have the following argument.
Operator norm of the matrix  is going to be bounded by
is going to be bounded by  , since
, since
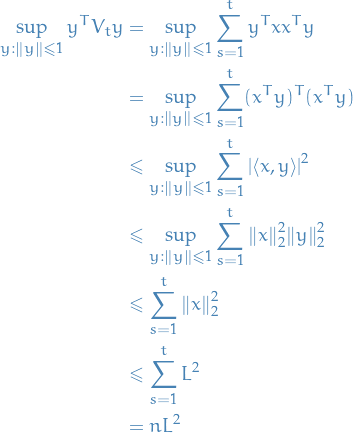
where in the third inequality we've made use of the Cauchy inequality and the assumption that 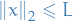 .
.
The factor of 2 shows up because we do

and each of these terms are bounded by 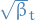 due to the vectors being in
due to the vectors being in  .
.
20.
20.1
Errata
- p. 79: in point 3), there's a sum without any terms…
Linear bandits
Contextual bandits
Batched bandits
- han20_sequen_batch_learn_finit_action
- Analysis of both adverserial and stochastic contexts (both with stochastic rewards)
- Finite number of arms
- Number of batches
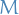 is allowed to scale wrt.
is allowed to scale wrt.  , and for the relevant results, they provide lower-bounds on the number of batches necessary to achieve the desired regret.
, and for the relevant results, they provide lower-bounds on the number of batches necessary to achieve the desired regret. - Analysis is done by analysing the prediction error of a linear regression model which has seen
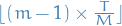 observations, where
observations, where  is the index of the batch. From this we can deduce the regret of following the predictions based on these previous observations rather than the online version.
is the index of the batch. From this we can deduce the regret of following the predictions based on these previous observations rather than the online version. - Algorithm presented is essentially LinUCB?
- Adverserial contexts
Lower-bound on the regret of any sequential batched algoritm for the case of
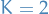 han20_sequen_batch_learn_finit_action
han20_sequen_batch_learn_finit_action
![\begin{equation*}
\sup_{\theta^{\ast}: \norm{\theta^{\ast}}_2 \le 1} \mathbb{E} \big[ R_T(\mathrm{Alg}) \big] \ge c \cdot \Bigg( \sqrt{d T} + \bigg( \frac{T \sqrt{d}}{M} \land \frac{T}{\sqrt{M}} \bigg) \Bigg)
\end{equation*}](../../assets/latex/bandits_3a4463e0017040596f4cda75f6cf1214efb45b9c.png)
where
 is the number of arms
is the number of arms is dimensionality of
is dimensionality of 
Reward is modelled as

where
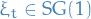 .
.
 is horizon
is horizon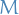 is number of batches
is number of batches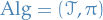 denotes the algorithm which consists of a "time-grid"
denotes the algorithm which consists of a "time-grid"  (with each "interval" in the grid corresponding to a single batch, so that
(with each "interval" in the grid corresponding to a single batch, so that  ) and
) and 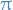 the learning algorithm/policy which maps previous observations to next action to take.
the learning algorithm/policy which maps previous observations to next action to take. is a universal constant independent of
is a universal constant independent of 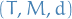
- Stochastic contexts
- Upper-bound on regret for what's essentially LinUCB han20_sequen_batch_learn_finit_action