Averaged Perceptron

Table of Contents

Overview

Averaged perceptron is a optimization algorithm which only has one hyperparameter: $N$, the # of iterations.

It will keep updating towards seperating the labels based on the inputs for as long as you specify, hence it's prone to overfit.

Notation

  • $\mathbf{x}$ - a single input vector, of $D$ dimensions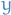
  • $y$ - a single label, $y \in \{-1, 1\}$
  • $x_d$ - the dth component of some input vector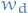
  • $w_d$ - weight for the dth component of the inputs
  • $b$ - bias

Algorithm

Training

  • $w_d \leftarrow o,\ \text{for all } d = 1 \dots D$
  • $b \leftarrow o$
  • for $1 \dots N$ do
    • for all $(\mathbf{x}, y) \in D$ do
      • $a \leftarrow \sum_{d=1}^D w_d x_d + b$
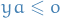      • if $y a \le o$ then
        • $w_d \leftarrow w_d + y x_d,\ \forall d = 1 \dots D$
        • $b \leftarrow b + y$
      • end if
    • end for
  • end for
  • return $w_0, w_1, \dots, w_D, b$

Test

  • $a \leftarrow \sum_{d=1}^D w_d \hat{x}_d + b$
  • return $\text{sign}(a)$