Approximate Bayesian Computation (ABC)
Table of Contents
Notation
 parameters
parameters generated samples from model with parameters
generated samples from model with parameters 
 denotes observed data
denotes observed data is the domain of the observations
is the domain of the observations is a metric on
is a metric on 
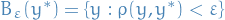
Overview
- Cases where computing the likelihood of the observed data
 is intractable
is intractable - ABC uses approximation of the likelihood obtained from simulation
Rejection ABC
Let  be a similarity threshold, and
be a similarity threshold, and  be the notion of distance, e.g. premetric on domain
be the notion of distance, e.g. premetric on domain  of observations.
of observations.
The rejection ABC proceeds as follows:
- Sample multiple model parameters
 .
. - For each
 , generate psuedo-dataset
, generate psuedo-dataset 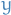 from
from 
- For each psuedo-datset
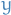 , if
, if 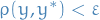 , accept the generated
, accept the generated 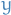 , otherwise reject
, otherwise reject 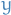 .
.
Result: Exact sample 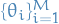 from approximated posterior
from approximated posterior  , where
, where

Choice of  is crucial in the design of a n accurate ABC algorithm.
is crucial in the design of a n accurate ABC algorithm.
Soft ABC
One can interpret the approximate likelihood  in rejection ABC as the convolution of the true likelihood
in rejection ABC as the convolution of the true likelihood  and the "similarity" kernel
and the "similarity" kernel 
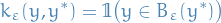
In fact, one can use any similarity kernel parametrised by  satisfying
satisfying

which gives rise to the Soft ABC methods:
Soft ABC is an extension of rejection ABC which instead weights the parameter samples from the model instead of rejecting or accepting.
An example is using the Gaussian kernel:

Which results in the weighted sample
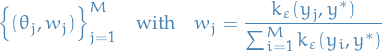
which can be directly utilized in estimating posterior expectations, i.e. for a test function 
![\begin{equation*}
\mathbb{\hat{E}} \big[ f(\theta) \big] = \sum_{i=1}^{M} w_j f(\theta_j)
\end{equation*}](../../assets/latex/approximate_bayesian_computation_fb1a65361822bd3a8a9eb9d66fb374dcf23af647.png)