Bonds

Table of Contents

Definitions

Z-spread

The zero-volatility spread is a single value that needs to be added to every spot yield on the curve in order to make the present value of the risky bond equal to the present value of the risk-free bond (Treasury bond).

That is, if the present value of the risk bond is $v_b$, then the Z-spread $z$ is the value such that

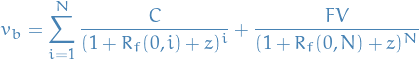
\begin{equation*} v_b = \sum_{i=1}^{N} \frac{C}{(1 + R_f(0, i) + z)^i} + \frac{FV}{(1 + R_f(0, N) + z)^N} \end{equation*}

where

  • $C$ denotes the coupon rate
  • $FV$ denotes the face-value (i.e. what we paid for the bond upon initial purchase)
  • $R_f(0, t)$ denotes the spot rate of maturity $t$ for a risk-free bond (not annualized)
  • $N$ is the number of "periods"

Say in the case where we had a bond for 4 yrs before it matured, which had a market price of 975:

  1 2 3 4
Cash flow 120 120 120 1120
Treasury spot rates (risk-free) 0.05 0.06 0.065 0.07
Discounted Cash Flow 114.28571 106.79957 99.341891 854.44264
Value of bond (at maturity)       1174.8698
Market price       975

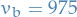Then the Z-spread is the value of $z$ in the such that $v_b = 975$ in the formula above. Hence, it's simply the "average" percentage more earnings compared to the risk-free bond.